不同权矢量下水声低频相控垂直阵远程探测性能的研究
2014-07-30李海峰马刘海军彭大勇赵文耀
李海峰马 力 曾 娟 刘海军 彭大勇 赵文耀
(中国科学院水声环境特性重点实验室 北京 100190)
1 引言
水声低频相控线阵是“单模(单号简正波)”激发的关健硬件设备之一,是伴随这一新概念性技术而生的新工具。通过开环或闭环算法控制相控阵单元的幅度及延迟,经声波相互叠加,可形成稳定的单模声场或有一定指向的多模声场,实现较高能效比的远程目标探测。现有的相控阵研究多集中在雷达方面,已经非常成熟;在医疗超声领域也有近三十年的研究历史;在浅海水声学方面,利用相控阵[1,2]进行单模激发的理论、实验与应用研究才刚起步。
自从上世纪70年代Bucker和Williams把简正波理论(normalmode)[3]引入水声传播声场计算以来,水声传播理论得到了飞速的发展,特别是浅海声传播的简正波理论是非常重要的,加之现在声纳主要向低频发展,更显简正波理论的重要性。八十年代美国的水声专家 Clay和 Huang[4]以及Gazanhes和Garnier[5]分别在实验室水槽里进行了相控阵激发单号简正波(单模)的试验,采用高频声源,反馈阵于近场,得到了很好的试验结果。2008 年,2010 年俄罗斯学者[6,7]利用小孔径垂直阵,结合空间滤波技术仿真研究垂直阵激发低号简正波。在国内,中国科学院声学研究所首先解决了相控阵宽带匹配[8]和一致性差问题,研制了用于浅海低频的相控垂直阵,并进行激发单号简正波的实验,取得了非常好的效果。经过近十年的理论与试验研究,在近距离上,单号模(简正波1号,2号,3号)闭环激发能量比达到95%以上,开环激发能量比达到90%以上,形成了一系列相控阵权矢量近场(反馈距离<3倍海深)控制算法。然而,利用相控阵进行远程探测时,如何选择所需的发射权矢量还缺乏深入的研究;对如何与常规主动声纳进行性能比较以及应用什么样的评估准则还有待研究。
前期的理论研究与试验工作同时表明,只要不超过单个相控阵阵元的发射极限,通过权矢量能够将相控线阵声纳与传统主动声纳统一起来。结合简正波理论与信号估计检测理论,本文将给出低频相控阵的浅海远程传播模型和性能评估方法。评价相控阵参数估计性能理论上有许多这样的限,本文采用参数估计方差下限即 Cramer-Rao界(即CRB)。在国外,文献[9-11]报导了已完成的相似工作。2001 年,Aleksandar[9]基于雷达(声纳)目标模型,从纯数学角度推导有源阵参数估计方差下限。1996年,Swingler[10]利用 CRB 评估两紧邻目标到达波方位估计性能。2011年,Saurav[11]研究利用最大信息矩阵设计方位估计最优阵形。在本文,首先推导相控阵为声源的声纳目标模型,其次,利用信息矩阵,建立参数估计CRB与权矢量关系式,最后,在输入相同能量条件下,仿真比较不同权矢量远场控制效果。首先依据简正波理论推导相控垂直阵声源远程传播模型,建立包含垂直阵权矢量的声纳目标模型;结合经典估计理论,推导复包络数据的回波时延和多普勒的Fisher矩阵,然后计算参数估计Cramer-Rao界;得到相控阵权矢量与目标参数估计CRB之间的关系,在此基础上,结合相控阵总能量一定条件,仿真对比分析相控阵三种工作模式下常规声纳(单个阵元发射)、全1(阵等幅度发射)、单号模相控(1,2,3号模加权发射)的远程探测参数估计性能。
2 理论推导
本节从简正波理论推导相控垂直阵远程传播模型,获得简谐点声源回波信号的频域表示后反付立叶变换(FT),推导包含发射权矢量的声纳目标模型。结合经典复数据估计理论,借助Fisher信息矩阵,推导统一在权矢量下相控阵距离估计与多普勒频移估计方差理论下限。由于采取的是相控阵不同加权矢量发射和垂直水听器阵接收,本文仅限于讨论目标距离与多普勒频移估计问题。
2.1 相控阵简正波传播模型
在水平分层的海洋环境中,以 e-iωt形式作振动的简谐点声源所激发的声场被表示为(忽略时间因子 e-iωt)

式中z为场点的深度,r声源的水平距离,z0为声源深度,ψm是简正波本征函数,H(1)0(·)是第一类零阶Hankel函数,km为本征值。如果水平距离远大于海深h,那么p(r,z)表示成有限个简正波的和,如下式:

其中PR是式中可忽略的部分。
简正波方程的解是一个复杂的特征值问题,KRAKEN方法采用有限差分方法求解方程,可以得到快速精确的离散解。已知海洋环境参数(声速剖面、海底海面声学参数)和点源的位置,声源的频率ω0,利用KRAKEN声场计算程序可以计算出单频点水声信道简正波本征函数ψm和本征值km。
对于一条沿深度分布N元低频相控垂直线阵,其所激发的单频声场被表示为:

式中wn为相控阵各阵元发射系数,将式(3)中各项写成矩阵形式,得到距低频相控线阵水平距离r,接收深度zl的声场表示为

其中 Q=[q1q2… qN],W=[w1w2… wN]T,运算符T为转置运算符,Q 里面元素 qn=。这样,相控阵激发频率为ω0的单频信号,在声场中点(r,zl)的频率响应值为

上式中考虑的是简谐点声源 S(ω)=δ(ω-ω0)。假设在(r,zl)处有目标,则在接收信号处(0,zk)收到目标回波信号,假设目标反射对信号频谱特性没有发生改变,回波经过接收信道响应p(r,zk,zl),反射波在接收点zk的信号频谱为

需要指出,阵声纳的发射信号,可以通过权矢量W的幅度和延迟来控制相干叠加或消稳,形成稳定的同向相加声场,减少在正向信道中衰减严重的能量激发,并使照射到目标上能量尽可能大(即提高探测目标入射波强度),这对远程目标探测是非常有意义的。通过权矢量W的不同取值,还可以讨论常规主动声纳,阵元全1发射和单模发射之间的能效,评估其优劣。选择相控阵声纳能效最优的发射权矢量Wopt也是需要研究的问题,本文暂不讨论。
2.2 参数估计的CRB
对相控阵声纳远程探测距离的无偏估计量的方差确定一个下限,这种性能评估方法提醒我们不可能求得方差小于下限的无偏估计量,这在信号处理的可行性研究中是常用的。存在许多的这样的限(McAulay and Hofstetter 1971,Kendall and Stuart 1979,Seidman 1970,Ziv and Zakai 1969),其中Cramer-Rao限(CRB)最容易确定。利用参数估计方差下限(CRB),评估相控阵不同权矢量远程探测参数估计方差特性,首先要建立CRB与权矢量关系式,具体推导见附录。开始推导前,对式(6)反FT变换转化为时域信号,提取时域信号复包络,并考虑加性噪声,得到经目标反射接收到复基带信号为:

其中x=Q(r,zl)W·TS·qk为接收信号复包络幅度,τ为接收信号时延,ωD为接收信号多普勒频移,e(t)为加性噪声,式(7)为声纳(雷达)目标模型。从附录式(A7)得相控阵权矢量与时延估计与多普勒估计CRB关系式如下:

由式(A7)可知,CRB(υ)可以简单分成两部分:(1)为回波信号幅度部分和噪声;逆矩阵为信号形式相关得成反比,这样就确立了相控垂直阵权矢量W与参数估计方差下限之间的理论关系。
由上面分析可知,通过提高入射声强,理论上能够使目标参数估计的方差下限降低。然而对于主动声纳来说,最大声源级是受限的,也就是说,主部分,隐含模糊度函数概念。对于如何选择发射信号的形式的第二部分,这里暂不讨论。由式(A7)可动声纳发射功率的增加并非无止境的(声空化、低频单换能器热极限以及匹配网络效率等限制)。多个阵元空间成阵最大功率发射能解决这个问题,但本文并不讨论。本文讨论的是在不超过单个换能器声源极限条件下,消耗相同能量条件下,实现最优的参数估计。用参数表示为WWH=C≤Ps下相控阵的参数估计性能。
3 仿真结果
仿真环境为:水深32.5 m,水中声速1520 m/s。海底密度 1.8g/cm3,声速 1680 m/s,纵波衰减1 dB/λ,信号为单频脉冲信号。间距为1.5 m的21元相控阵,第一个换能器布于水下1.5 m,最后一个位于水下31.5 m。就近布放间距1.0 m的32元垂直水听器阵,第一个距水面1 m,最后一个在水下32 m。在距离相控阵10 km处放置水声应答器模拟目标反射,应答器增益为0 dB。中心频率为600 Hz时,简正波号数为17,频率900 Hz时,简正波号数为25,模拟环境噪声为高斯白噪声,环境参数示意图如图1所示。

图1 仿真声场环境示意图Fig.1 Schematic diagram of sound field simulating environment
仿真过程中,先根据KRAKEN声场计算程序计算出简正波本征函数ψm和本征值km,然后利用式(8)计算不同目标深度,垂直水听阵接收信号形式,比较相控阵相同输入能量条件下,权矢量为单模(1,2,3号模),全1和单个阵元模式下接收回波的强度。选取相控阵发射系统总能量C为1,相控阵阵元间一致性完好,此时全1发射权矢量为为N×1列1矩阵;对于单模发射,ψ(z)为本征函数沿深度采i样,i=1,2,3;对于单个换能器权矢量为单个 1,并选取深度分别为上(9 m)、中(18 m)、下(27 m)三个位置相控阵阵元加权系数为1,其它阵元为0,权矢量记为W4、W5、W6进行仿真比较。
相控阵各种权矢量发射模式具有相同的目标回波特性,所以在利用简正波分解时,只分析了反射目标处虚拟垂直水听器阵接收的入射声场特性,讨论不同权矢量发射下接收声场强度。分别选择目标位置为10 km、20 km、30 km,两种频率 600 Hz、900 Hz仿真计算接阵得到的幅度归一化声能分布(以不同接收声能中,最大值作归一,仿真中没有指明具体信噪比,只指出在相同噪声级条件下,相控阵不同权矢量发射下,接收的信号分布)如图2-7所示,图中图例为W0:权矢量为W0的全1模式;W1:权矢量为W1的1号模模式;W2:权矢量为W2的2号模模式;W3:权矢量为W3的3号模模式;W4:位于9 m深度单阵元模式,W5:位于18 m深度单阵元模式;W6:位于27 m深度单阵元模式。对W0相控阵发射模式的权矢量进行简正波分解,得到600 Hz、900 Hz,1-5 号模的能量系数如表1所示,总能量为1。
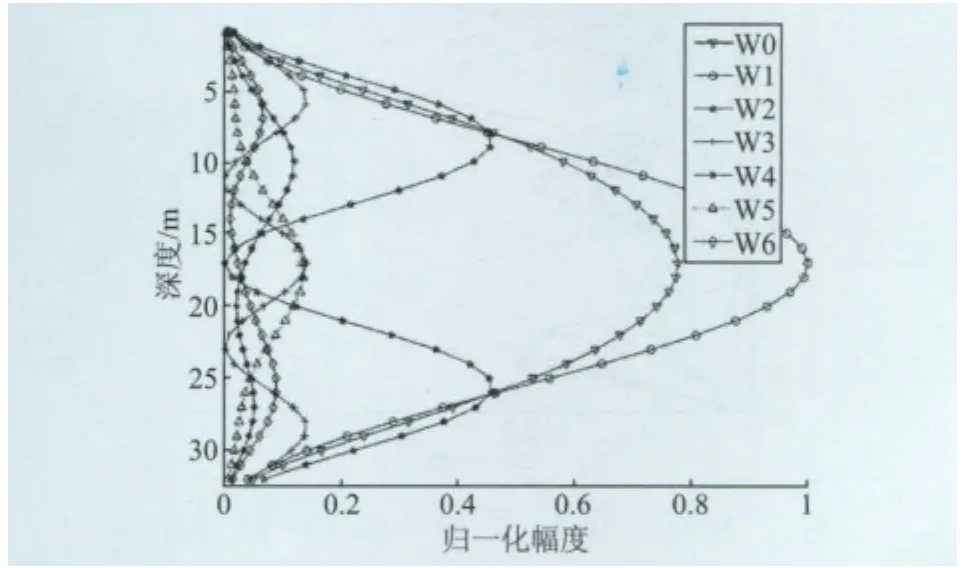
图2 接收阵10 km处,600 Hz归一化声能Fig.2 Receiving normalized acoustical energy distribution of 600Hz at 10km

表1 全1发射权矢量简正波分解1号-5号模能量Table 1 The normalmode decom position of W0

图3 接收阵20 km处,600 Hz归一化声能Fig.3 Receiving normalized acoustical energy distribution of600 Hz at20 km

图4 接收阵30 km处,600 Hz归一化声能Fig.4 Receiving normalized acoustical energy distribution of600 Hz at30 km

图5 接收阵10 km处,900 Hz归一化声能Fig.5 Receiving normalized acoustical energy distribution of900 Hz at10 km

图6 接收阵20 km处,900 Hz归一化声能Fig.6 Receiving normalized acoustical energy distribution of900 Hz at20 km

图7 接收阵30 km处,900 Hz归一化声能Fig.7 Receiving normalized acoustical energy distribution of900 Hz at30 km
直观上入射目标的声能越强,目标参数估计的方差越小,同样的,理论推导也证明了CRB也越小。由图2-7可知,相同发射能量下,利用单个换能器实行远程目标探测,其效果是非常差的,这里就不再讨论了。W2、W3模式由于本征值km虚部较W1模式本征值值大(掠射角大),具有较大衰减。远程探测时10 km处,600 Hz、900 Hz的2号模基本上衰减到1号模能量的50%,3号模衰减到1号模能量20%-30%。更远程探测时,由表1-表3可知,高号模基本上衰减掉了。由表1可知,W0模式权矢量简正波分解1号模占86%左右,远程传播后,表2-表3所示,基本上只剩下1号模了(95%以上)。

表2 600 Hz,相控阵全1权矢量发射,距离10 km,20 km,30 km简正波分解Table 2 Phased array em itting 600 Hz signal,the normalmode decomposition results of receiver array at 10 km,20 km,30 km

表3 900 Hz,相控阵全1权矢量发射,距离10 km,20 km,30 km简正波分解Tab le 3 Phased array em itting 900 Hz signal,the normalmode decomposition results of receiver array at 10 km,20 km,30 km
4 结论
基于简正波理论推导了水声低频相控垂直线阵远程探测的声传播理论模型,将远程探测声场统一成相控阵权矢量函数的形式。利用经典估计与检测理论,导出了目标距离和多普勒频移估计方差的理论下限表达式。理论和仿真分析结果表明,远程探测的相控阵模式相比于常规单阵元模式有较高的能效比,是相对高效的探测声源。浅海水下波导中,相控阵单模加权发送,特别是1号模加权具有更远的探测距离和参数估计方差下限。
目前,本文仅仿真比较七种权矢量下相控阵发射结果,1号模权矢量发射下具有较好的远程探测性能,但是否是最优的权矢量,还有待进一步理论研究。
致谢本文工作内容得到了声学所高天赋研究员的指导,特此表示感谢。
[1]BUCK J R.Single Mode Excitation in the ShallowWater Acoustic Channel Using Feedback Control[D].Doctoral Dissertation of the Massachusetts Institute of Technology and the Woods Hole Oceanographic Institution.MIT/WHOI 97-07,1997.
[2]GINGRAS D F. Single mode excitation,attenuation,and backscatter in shallowwater[J].J.Acoust.Soc.Am.,1998,103(1):195-204.
[3]WILLIAMS A.O. Normal-mode methods in propagation of underwater sound[M].in Underwater Acoustics.NewYork:STEPHENSRWB(Wiley-Interscience),1970.23-56.
[4]CLAY C S,HUANG K.Single mode transmission and acoustic backscatteringmeasurements in a laboratory waveguide[J].J.Acoust.Soc.Am.,1980,67(3):792-794.
[5]GAZANHES C,GARNIER J L.Experiments on single mode excitation in shallowwater propagation[J].J.Acoust.Soc.Am.,1981,69(4):963-969.
[6]GOLUBEVA E V,ELISEEVNIN V A.Generation of a single normal wave by a vertical linear array in the water layer[J].Acoustical Physics,2008,54(1):52-57.
[7]GOLUBEVA E V,ELISEEVNIN V A.Emission of a single normal wave by a vertical discrete linear array in the pekeris waveguide[J].Acoustical Physics,2010,56(1):66-71.
[8]高天赋,曾娟.压电陶瓷发射换能器的Butterworth匹配定理[J].声学学报,2006,31(4):297-304.GAO Tianfu,ZENG Juan.A theorem on Butterworth matching for piezoelectric ceramic emission transducer[J].ACTA ACUSTICA,2006,31(4):297-304.
[9]ALEKSANDAR D.Cramer-Rao bounds for estimating Range,velocity and direction with an active array[J].IEEE Trans on Signal processing,2001.6,49(6):1122-1137.
[10]SWINGLER D N,GREGORY S.A generalized approximation for the Cramer-Rao lower bound on direction-of—arrival estimates for a pair of closely spaced sources[J].J.Acoust.Soc.Am.,1996.8,100(2).Pt.1:918-924.
[11]SAURAV R,TULADHAR,JOHN R BUCK.Optimum array design to maximize Fisher information for bearing estimation[J].J.Acoust.Soc.Am.,2011.11,130(5):2797-2806.
附录 CRB与相控阵权矢量关系式
从式(7)的声纳目标模型出发推导相控阵时延估计和多普勒频移估计方差的理论下限与相控阵发射权矢量关系式。为了方便数值分析,离散式(7)前,有如下信号噪声模型和有效的基本假设:
假设一个水听器接收到已知复带通信号(s(t)exp(jΩct),Ωc调制角频率)的扩展的、多普勒频移和时延的回波信号。并已知时延和多普勒频移ΩD(假定目标径向定速移动),目标距离r和径向速度vr有,c为声速。定义连续信号s(t)的采样信号s(n)=s(nΔt),Δt是采样间距。定义离散时延和多普勒频移为nr=τ/Δt,ωD=ΩD·Δt。将回波信号采样,变为离散时间为

这里,n=1,…,N包括整个相关处理间隔(CPI:Coherent processing interval),TCPI=NΔt,x 是复包络幅度(窄带内不变),未知确定常数,e(n)是加性噪声。式(A1)需满足条件v/c≪1,复包络满足WdT≪c/2v(Wd带宽,T脉宽,也就是说条件满足后,则径向速度对复幅度x的影响可忽略,归结为窄带信号假设)。
式(A1)被称为离散声纳(雷达)目标模型,这里假定x是确定的,然而,x亦是可以建模为零均值高斯随机变量的。因为在一个CPI内无需对x做过多的假设,所以不考虑多个CPI内x的分布。根据式(A1)模型,从Fisher信息矩阵入手推导目标时延估计,多普勒频移估计的CRB表达式。将式(A1)写成矢量形式如式(A2):

这里,υ=[ωDnτ]T,γ=[Re{x}Imag{x} υT]T,μ[n,γ]=x·exp(jωDn)s[n - nτ],y=[y[1]T,y[2]T…y[N]T]T,e=[e[1]T,e[2]T…e[N]T]T,μ(γ)=[μ[1,γ]Τ,μ[2,γ]Τ…μ[N,γ]Τ]Τ,φ(υ)=μ(γ)/x,上角标T是转置运算符。加性噪声项e假定是零均值复高斯,方差为:E(ee*)=C,E(y)=μ(γ),Cy=E(yy*),上角标*为共轭运算符。根据复数据的经典估计理论,复数据的复高斯概率分布函(PDF)数为

因Cy(υ)=C,可得Fisher信息矩阵:

式(A4)中各项偏导有如下表达式:

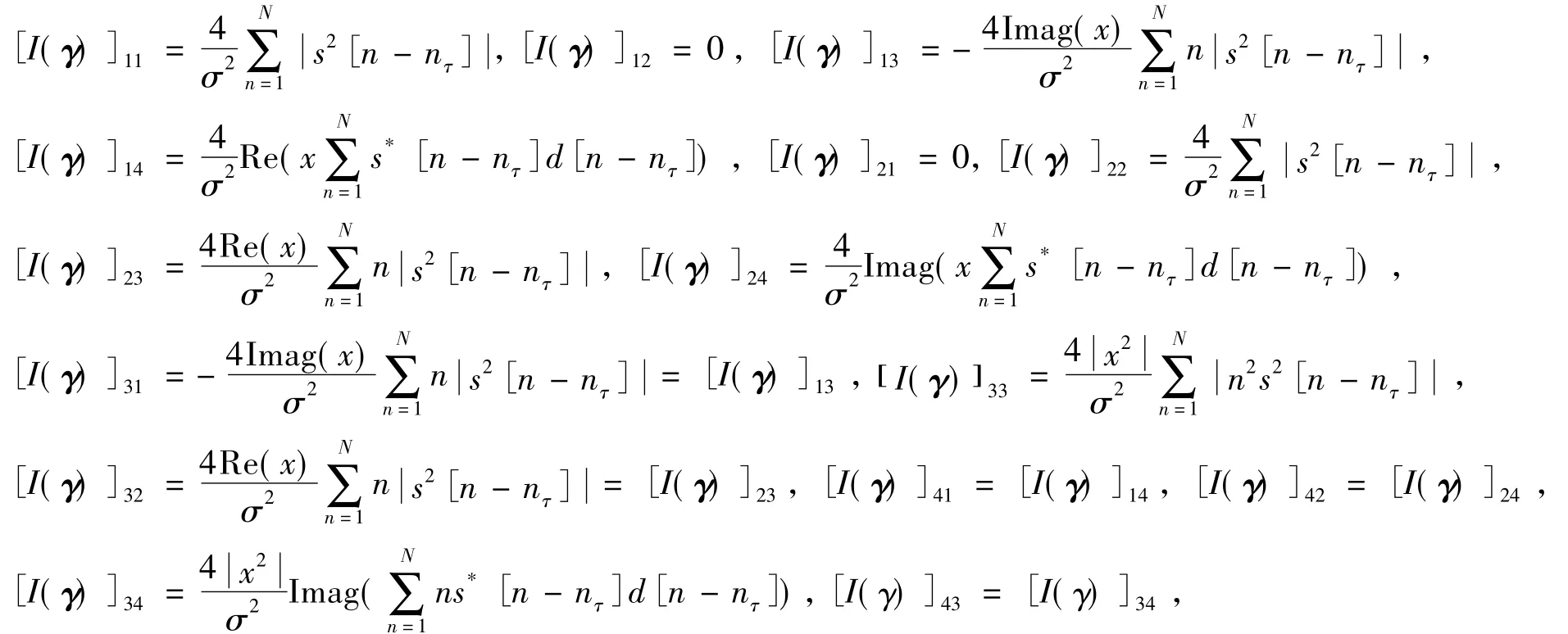

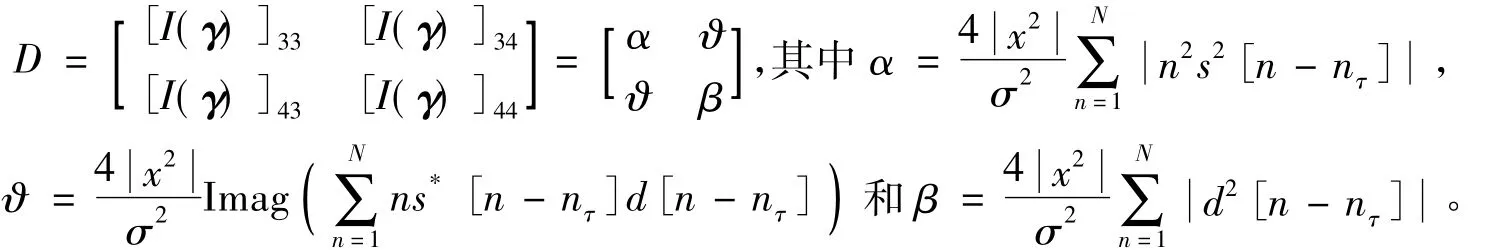
此时Fisher信息矩阵转化为分块矩阵为

从式(A5)可得,CRB(γ)=I(γ)-1,所以

这里只关心多普勒频移ωD和时延项nτ,所以

上式逆矩阵中各元素为 Γij,i=1,2;j=1,2,具体如下:
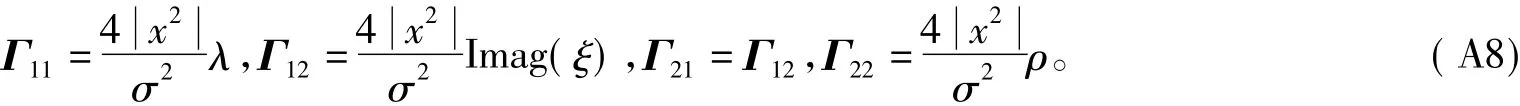
由此可得

到此为止,本文推导了相控阵发射权矢量与参数估计方面差下限关系式。通过距离时间关系r=cτ/2,可以得到目标距离估计的CRBrr与时延估计的CRBττ为

