高速铁路高架桥局部振动的有限元分析

罗文俊，张辛元

（华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌330013）

高速铁路高架桥局部振动的有限元分析

罗文俊，张辛元

（华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌330013）

针对高速铁路高架桥箱型梁局部振动问题，基于车辆—轨道耦合动力学原理，采用实体单元对梁体进行有限元分析。通过对选取的六个敏感点振动特性的研究，比较得出箱梁各部位局部振动情况。研究在不同列车速度作用下，梁体不同部位的时域与频域响应，得出随车速变化各点振动频率的分布规律。同时分析轨道状态对箱梁局部振动的影响，对比计算结果可知，轨道不平顺是引起局部振动的主要因素。此外，还分析了不同边界条件对箱梁的局部振动响应的影响，结果表明固支梁相比简支梁，顶板、腹板、底板的局部振动响应有所减弱，而对翼缘板则影响较小。

振动与波；箱梁；局部振动；不平顺；边界条件；有限元方法；

高速列车通过高架桥梁引起桥梁的低频整体振动与高频局部振动，而局部振动是结构噪声的主要产生根源[1]。目前对于桥梁结构噪声的理论分析以统计能量法与边界元法为主，或通过噪声试验进行研究[2]，从局部振动出发对结构噪声的研究则较少。关于桥梁整体振动研究较为成熟，对局部振动的相关研究主要集中在基本的传播规律及产生机理上[3]。本文采用有限元法，结合车辆—轨道—桥梁耦合振动理论对典型箱梁局部振动进行细化研究，对局部振动特性进行了时域、频域分析，并对相关影响因素进行了对比分析，同时对有限元模型边界条件的选取及对研究结果的影响进行了分析。

1 计算模型

1.1 有限元模型的建立

本文以某高速铁路32 m跨径双线简支箱型桥梁为原型建立实体有限元模型，其结构尺寸如图1。

为更好反应梁各部位振动响应，梁体、CRTSⅡ型轨道板均采用实体单元solid 45单元，钢轨采用beam 188单元，扣件与CA砂浆采用弹簧单元combine 15单元，有限元模型见图2。

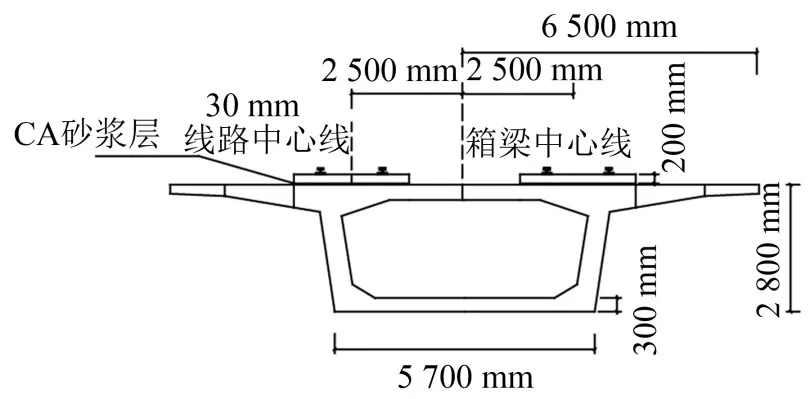
图1 箱梁相关结构尺寸

图2 箱梁有限元模型

因研究主要考虑箱梁的局部振动，故对桥墩及附属构件不予考虑，各项参数见表1。

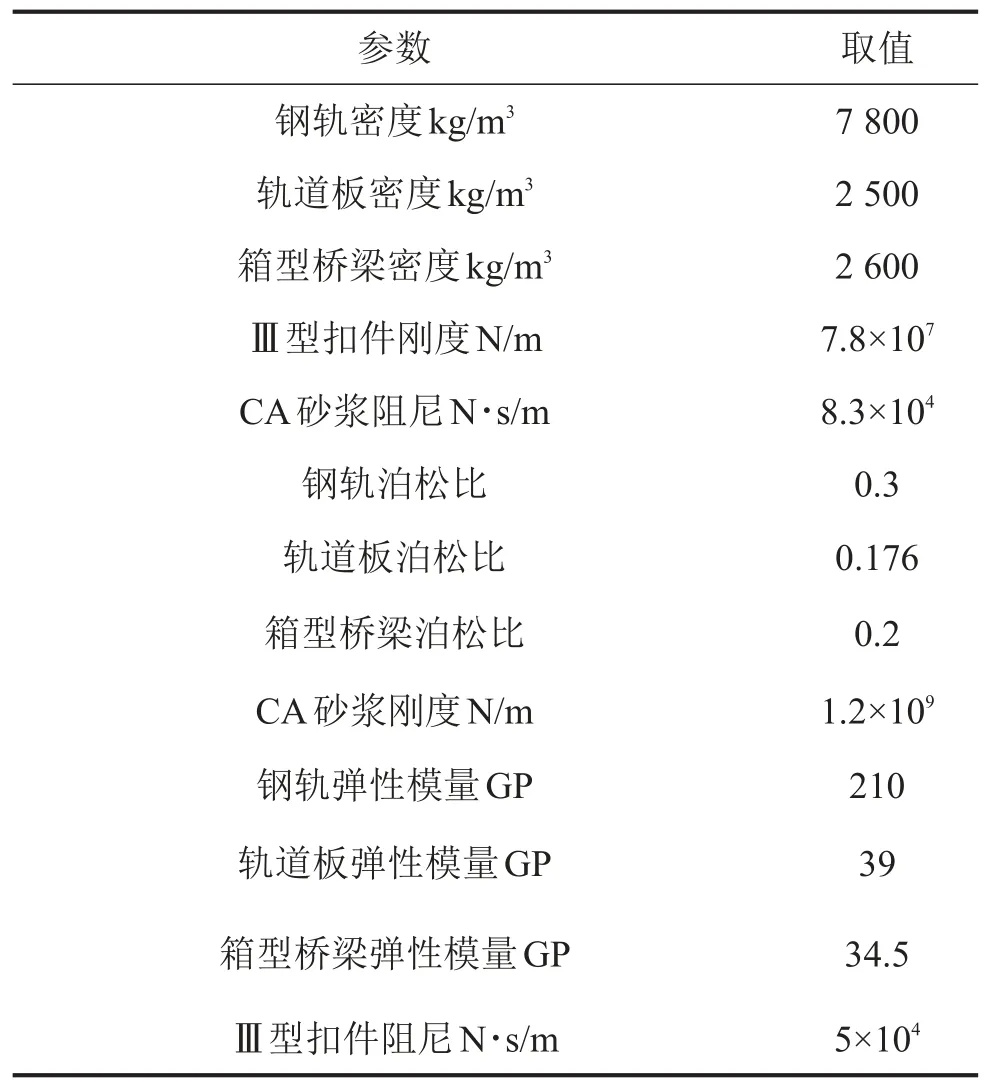
表1 无砟轨道与桥梁结构参数

1.2 车轨桥耦合模型

本文采用文献[4]提出的车辆—轨道—桥梁新模型，将每节车辆离散为4个具有二系悬挂的独立动轮单元，车体、转向架和车轮均考虑为刚体，只考虑其沉浮振动，轮轨之间为弹性接触。为更好的反应箱梁局部振动特性，分别对平顺状态、不平顺状态进行计算，采用CRH3列车，模拟行车速度从230 km/ h～410 km/h，间隔为20 km/h，根据此模型计算各种工况的轮轨作用力[5]。平顺状态下轮轨作用力随车速增大基本不变，稳定后的数值均在69.7 kN附近小范围浮动[6]。瞬态动力分析取稳定后的数值进行加载。不平顺状态采用德国高速低干扰谱作为轮轨表面的不平顺激励。采用陈果提出的轨道不平顺谱数值模拟新方法得到不平顺样本[7]。表2列出了在不同车速时的最大轮轨作用力。从表中可以看出轮轨力随着车速增大而增大。

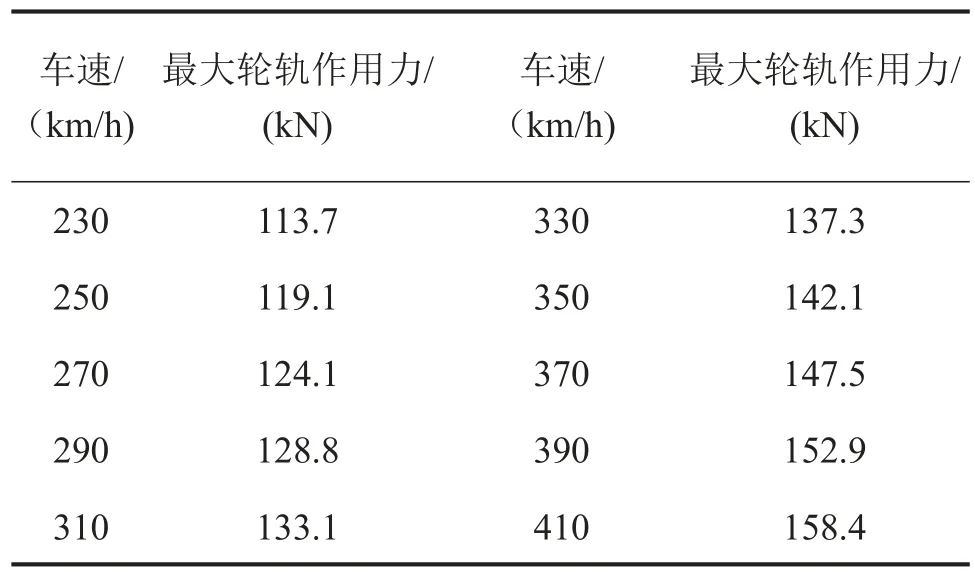
表2 不同车速时的最大轮轨作用力

将得到的轮轨作用力导入Ansys软件中，选取4节列车，按车轮位置分布，将荷载加载于钢轨有限元模型上进行瞬态动力分析。

2 箱梁自振分析

通过对上述模型进行模态分析，得出梁前500阶自振频率，频率范围为0～401.2 Hz。其中前10阶自振频率与振型描述如下。

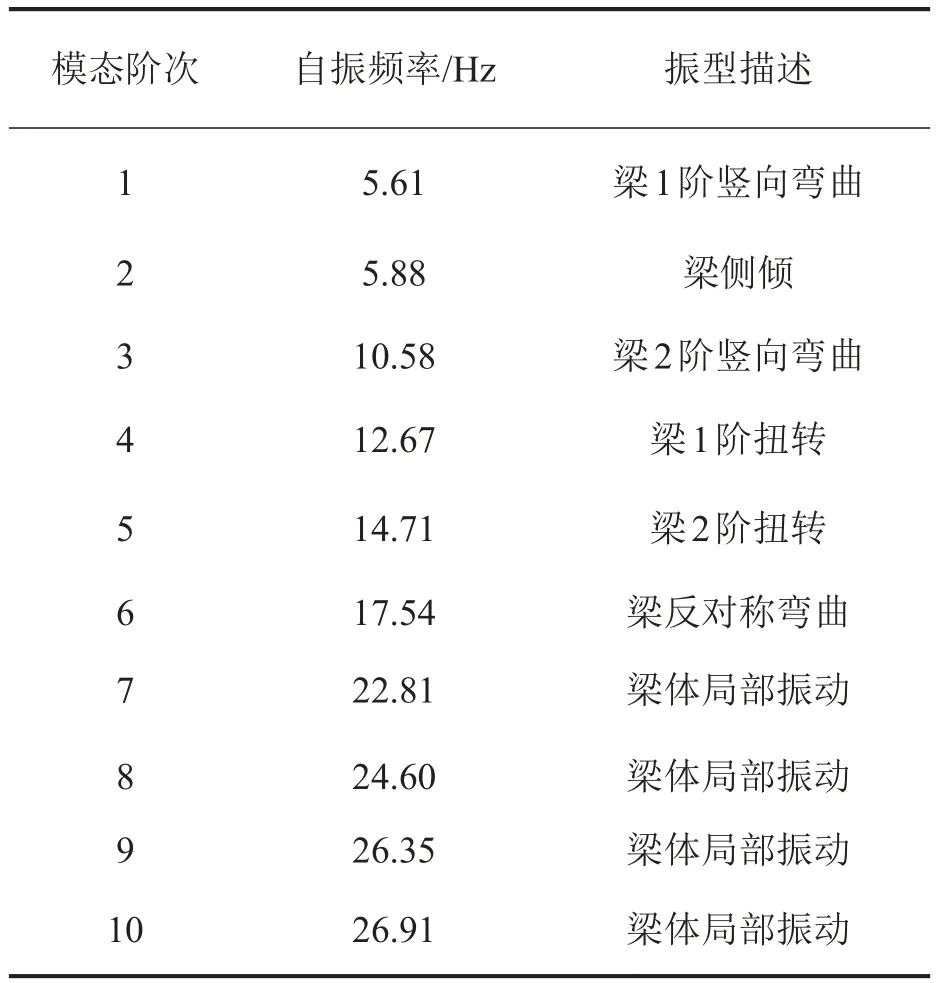
表3 前10阶振型描述

可看出前6阶为梁的整体振动，之后均为梁体的局部振动。因而局部振动相对来说属于高频振动。

3 轨道状态对桥梁局部振动影响

进行瞬态动力分析时，选取箱梁跨中截面的六个敏感点如图3所示。根据模态分析结果选取500阶模态，采用模态叠加法对有限元模型进行瞬态动计算[8]。

图3 敏感点分布图

3.1 轨道平顺状态

(1)对计算结果分析得到不同车速下各敏感点最大加速度及加速度有效值如图4 a与图4 b。

图4 a最大加速度随车速变化图

图4 a反映了在平顺状态下随车速增大，各敏感点最大振动加速度逐渐增大。振动加速度有效值作为振动强度指标，能较好的反映各点振动幅度[8]。

图4 b加速度有效值随车速变化图

图4 b中各点加速度有效值随车速增大而增大，且各点变化幅度基本一致。综合图4 a、b，在相同的车速下，各敏感点振动加速度递增顺序为：敏感点2、敏感点1、敏感点4、敏感点5（四五两点相近）、敏感6、敏感点3。

(2)选取车速为230 km/h，270 km/h，310 km/h，350 km/h，390 km/h时跨中截面各输出点振动加速度进行频谱分析，由于平顺状态下各敏感点的加速度频谱图相类似，在此只列出敏感点一的频谱图，如图5：

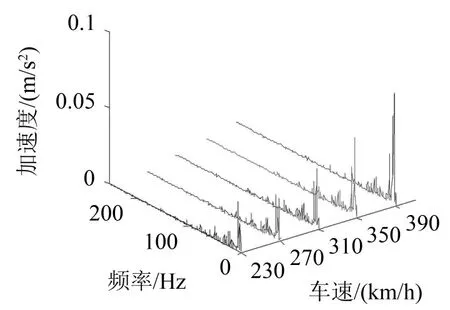
图5 敏感点1不同车速振动加速度频谱图

由频谱分析可得出对于箱梁各位置的振动频率均主要集中在0～189 Hz之间，在0～22 Hz的频段内，从自振分析得出结果可看出该频段对应的振型属于箱梁的整体结构受迫振动。大于189 Hz，对应的幅值很小可以忽略。且在同一车速下，六个敏感点在相同频率处出现振动峰值。将这些频率与自振分析结果进行对比，可知各点局部振动频率主要集中在22 Hz～189 Hz之间。

3.2 轨道不平顺状态

(1)轨道不平顺状态下不同车速下各点最大加速度及加速度有效值如图6。

图6 a最大加速度随车速变化图

从图6 a中可以看出轨道不平顺状态相比平顺状态下，各敏感点的最大加速度值都相应增加10倍左右。由此可知轨道的不平顺是箱梁局部振动的主要因素。随车速增大，各敏感点最大振动加速度逐渐增大。车速在410 km/h时，敏感点三的最大振动加速度为3.37 m/s2，敏感点二处最大振动加速度为1.09 m/s2，没有超过我国规范规定的5 m/s2限值。

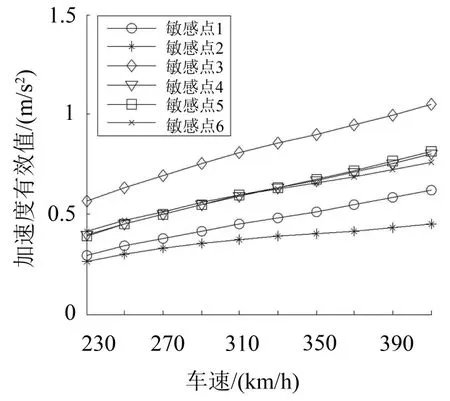
图6 b加速度有效值随车速变化图

图7 不同车速振动加速度频谱图

从图6 b中可以看出，敏感点3的振动加速度有效值明显大于其它点。箱梁翼缘板处振动幅度最大，同时可知敏感点2处的振动幅度最小。且车速的增大对敏感点2的影响较小，对敏感点6的影响较大。

(2)对跨中截面各输出点振动加速度进行频谱分析，如图7所示。

从不平顺状态下的振动加速度频谱曲线可知，箱梁各敏感点振动频率主要集中在0 Hz～199 Hz之间。在0 Hz～22 Hz内，同样出现较大的峰值，为梁体的整体受迫振动。相比平顺状态，箱梁整体振动的频段没有变化，局部振动频率分布区间有所扩大。两种轨道状态下各车速对应局部振动频段如表4。

从表4也可看出，随着车速的增加，箱梁局部振动主频分布区间上下限会随着车速增大而相应的增加。

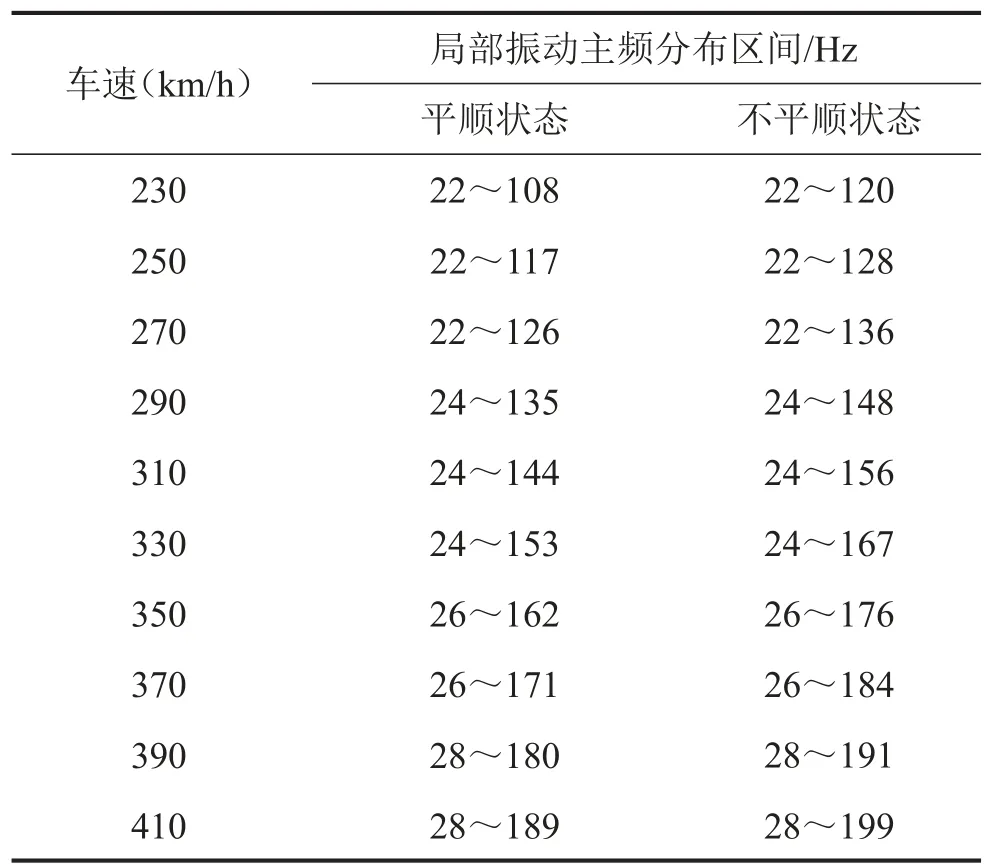
表4 频谱区间分布

4 边界条件对局部振动影响

下面将对比简支与固定两种边界条件，箱梁局部振动响应的不同。这里所说的固定边界指箱梁两端约束了六个自由度。表5列出了两种边界条件下的前7阶自振频率，对比可以看出固定边界条件下箱梁自振频率有所增加，主要由于箱梁在固定边界时的约束更强[9]。

表5 前7阶自振频率

表6列出了各个敏感点在两种边界条件下的最大振动加速度。从表中可以看出固支梁的振动响应整体上要比简支梁小。根据第三栏中梁不同部位加速度降低的百分比可知，第3、第6敏感点所受影响较小。表明采用固支梁对于控制箱梁顶板、底板、腹板局部振动有较好的效果，而对两侧翼缘板则效果不明显。

5 结语

（1）建立了实体有限元模型对箱型梁的局部振动进行分析，同一车速和轨道状态下，对比六个敏感点振动情况，翼缘板的振动较其它部位强烈，底板振动最弱；

（2）随车速增加，箱梁局部振动幅度会相应增大。局部振动的频段主要集中在22 Hz～200 Hz；同时箱梁局部振动主频分布区间上下限会随着车速增大而相应的增加；

（3）轨道不平顺是引起箱梁局部振动的主要因素。对比发现轨道不平顺对箱梁的局部振动幅度有较大影响，同时相比轨道平顺状态，局部振动频段区间上限有所增大；

（4）边界条件中选取固支梁相比简支梁，顶板、腹板、底板的局部振动响应有所减弱，而对翼缘板则影响较小。

[1]LEE Y.Y.,K.W.Ngai,C.F.Ng.The local vibration modes due to impact on the edge of a viaduct[J].Applied Acoustics,2004,65∶1077-1093.

[2]李小珍，尹航，吴金峰，等.成灌快铁高架桥梁区段噪声测试[J].噪声与振动控制，2013，02：183-187.

[3]卢祝清，刘林芽，黄志和.高速铁路噪声预测方法及其在昌九城际轨道交通中的应用[J].噪声与振动控制，2009，03：82-85.

[4]SHAO Wen-jie,LIU Lin-ya,ZHANG Bin.Analysis of dynamic response to simple-supported beam under high speed train,ISMR’2012-Proceedings of the Third International Symposium on Innovation&Sustainability of Modern Railway[C].Nanchang,East China Jiaotong University,China Railway Publishing House,2012,138-142.

[5]罗文俊，雷晓燕，练松良.基于FE-SEA混合法的无砟轨道桥梁系统垂向振动分析[J].铁道学报，2013，35(8)：94-101.

[6]雷晓燕.铁路轨道结构数值分析方法[M].北京：中国铁道出版社，1998.

[7]陈果，翟婉明.铁路轨道不平顺随机过程的数据模拟[J].西南交通大学学报，1999，34(2)：138-141.

[8]李奇.车辆—桥梁/轨道系统耦合振动精细分析理论及应用[D].上海：同济大学，2008.

[9]张迅.轨道交通桥梁结构噪声预测与控制研究[D].成都：西南交通大学，2012.

Analysis of Local Vibration for High-speed
Railway Bridge by Means of Finite Element Method

LUO Wen-jun，ZHANG Xin-yuan

（Engineering Research Center of Railway Environment Vibration and Noise,Ministry of Education East China Jiaotong University,Nanchang 330013,China）

∶Based on the theory of vehicle-track coupling dynamics,the local vibration of a box-girder of a high-speed railway bridge is analyzed by means of the Finite Element Method(FEM)with solid elements.Through the study of vibration characteristics of the 6 sensitive points,the local vibration in different parts of the box-girder is figured out.The responses of the different parts of the box-girder in time domain and frequency domain at different train’s speeds are analyzed.Furthermore,the influence of track’s irregularity on local vibration response is analyzed.The results show that the track’s irregularity is the main influencing factor for local vibration.Finally,the effect of local vibration on the boundary condition is discussed.It shows that the responses of the upper panel,the lower panel and the web panel of the fixed box-girder are weaker than those of the simply supported box-girder,but the responses of the flange panels of the two girders are nearly the same.

∶vibration and wave;box-girder;local vibration;track irregularity;boundary condition;FEM

U238< class="emphasis_bold">文献标识码：ADOI编码：

10.3969/j.issn.1006-1335.2014.06.033

1006-1355(2014)06-0148-05

2014-05-12

国家自然科学基金项目（51108180）；

江西省自然科学基金：(2011BAB212002)

罗文俊（1979-）,女,黑龙江哈尔滨人，副教授,主要研究方向：轨道动力学。

E-mail∶lwj06051979163.com