附加黏滞阻尼器的框架结构地震响应分析

赵子斌

（安阳职业技术学院建筑冶金工程系，河南 安阳 455000）

附加黏滞阻尼器的框架结构地震响应分析

赵子斌

（安阳职业技术学院建筑冶金工程系，河南 安阳 455000）

考虑到地震动具有随机性，利用平稳过滤白噪声地震动模型，首先建立黏滞阻尼结构的动力方程，运用虚拟激励法将平稳随机地震激励转化为简谐振动分析，求解黏滞阻尼结构在随机地震作用下的响应，然后通过选用相同数量的阻尼器在最大层间位移处集中布置、循环布置、权数布置三种布置方案，对比分析布置前后结构的地震反应，得出最优的黏滞阻尼器空间位置布置方案。由此可知黏滞阻尼器具有明显的减震效果，得到的黏滞阻尼器布置建议对抗震设计和加固具有参考意义，同时使用虚拟激励法能高效快捷的求出结构的随机响应。

消能减震；黏滞阻尼器；虚拟激励法；随机地震反应；优化设计

结构减震控制就是通过在结构上安装耗能减震装置减轻或抑制结构由于外荷载作用引起的反应。黏滞阻尼器是为结构体系提供附加阻尼，通过黏滞介质和阻尼器结构部件的相互作用产生阻尼力，达到耗散地震输入能量的目的，保证结构构件安全[1-3]。目前对于黏滞阻尼结构的应用研究已经涉及很多工程中，李春祥、徐双正等[4]使用时程分析法对安装非线性液体黏滞阻尼器的宁夏电视塔进行动力时程分析，评价其减震效果。王志强、胡世德、范立础[5]以东海大桥为实际工程背景，利用动力时程分析法分析比较增设黏滞阻尼器前后，结构在地震力作用下的地震响应和结构构件的地震力。陈建斌、丁浩民[6]对于复杂方钢管混凝土高层建筑通过不同加速度峰值和不同地震波作用下的时程分析，获得了结构从小震到大震下的动力响应，与无控结构相比，得到了黏滞阻尼器的耗能减震效果，总结评价了结构的整体抗震性能。Bracci等[7]对用黏弹性阻尼器进行钢筋混凝土结构抗震加固作了研究，提出了带有该阻尼器的钢筋混凝土结构的非弹性分析方法，分析了黏弹性阻尼器支撑对结构反应的影响。Toutch等[8]也进行了用黏弹性阻尼器加固非延性钢筋混凝土框架的研究。这些工程大多数是基于反应谱法和时程分析法等确定性分析方法。考虑到地震动具有明显的随机性，而不是确定的时间函数，从而导致结构的地震反应为随机反应。本文采用林家浩教授的虚拟激励法[9]，选用相同数量的黏滞阻尼器通过不同的布置方案，分析对比非减震结构与减震结构在随机地震作用下的地震反应，并得到最优的空间布置方案。

1 黏滞阻尼结构的动力方程

将附设黏滞阻尼器的结构看成多自由度层间剪切模型，运动方程为

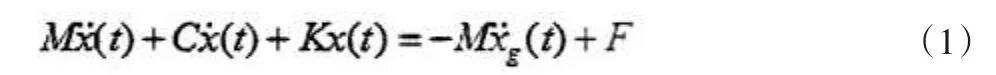
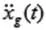
楼层由低向高编号，总层数为N，第J层质量为mj

第J层刚度为kj。

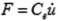
2 地震动模型

本文采用日本学者Kanai-Tajimi提出平稳过滤白噪声模型。该模型考虑了地表土层特性对地震动频谱特征的影响[10]。

3 虚拟激励法

工程应用中，若假定外部激励是一个平稳随机过程，则一般给出它的自功率谱密度函数Syy（ω），从而可以计算出结构重要的位移、内力等响应量的功率谱密度。文中利用虚拟激励法[9]将式（2）的功率谱离散化，对每个离散点构造虚拟地面加速度激励：

将（2）代入（1），得：

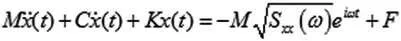
则结构响应功率谱为离散数值解为：

因此，各层间位移的响应自谱密度可利用上式得到。虚拟激励法的实质就是将平稳随机振动分析转化为简谐振动分析。由于对应零均值输入的结构，其响应均值也为0，由维纳-辛钦关系得：

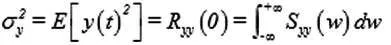
4 算例分析

某六层框架结构建筑，考虑地震烈度为8度（设计基本地震加速度值为0.2 g），Ⅱ类场地，设计地震分组为第三组，质量从低到高依次为1-3层12.808×105kg，4-6层7.911×105kg，层间刚度为10.28×105kN/m、9.81×105kN/m、9.47×105kN/m、7.52×105kN/ m、7.41×105kN/m、7.2×105kN/m、层高均为3.6m。黏滞阻尼器等效线性化后的等效阻尼为2.25×103kN·s/m。地震动模型参数根据场地类型选取特征阻尼比εj=0.72，场地的特征周期wj=13.96 rad/s峰值因子S0=11.106 cm2/s3[10]。对该框架结构安装6个黏滞阻尼器，采用三种方案布置，通过比较选择合适的布置方案。

方案一：在结构最大层间位移处集中布置3个阻尼器；

方案二：循环布置，在结构最大层间位移处循环布置，依次布置的顺序为4、1、2、3、5、6；

方案三：权数布置，通过结构每层层间位移角占总位移角的比例来布置，即1、4、5、3、5、2、6。

采用虚拟激励法，用MATLAB编程分别对无控结构和减震结构进行随机响应分析，得到两种结构的楼层位移，层间位移和层间剪力的响应均方差，图1、图2、图3。

图 1 结构各楼层位移响应均方差比较

图1 表明三种方案都能有效地减小结构楼层位移，并且顶层位移都相应的减小，其中方案二减小顶层位移的效果最明显。

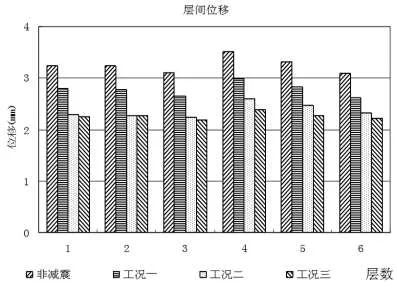
图 2 结构各层层间位移均方差比较

图2可知：加黏滞阻尼器前，结构最大层间位移楼层为第4层。

布置后，方案一，结构1-6层层间位移均较大幅度的减小，第4层减小最多，但是同时斜撑也增大了该层的层间刚度；方案二，结构各层的层间位移均减小，其中第4层减小最多，并没有造成某一层层间位移比原结构增大；方案三，各层层间位移均减小，其中第4层减小最多。

图 3 结构各层层间剪力均方差比较

由图3可知：加黏滞阻尼器之前，结构最大层间剪力楼层为第1层。

对于方案一，由于黏滞阻尼器集中布置在第1层，所以该层的层间剪力减小最多，但是同时斜撑也增大了该层的层间刚度，使结构的竖向刚度发生突变；方案二，结构各层层间剪力均减小，其中第4层减小最多。方案三，层间剪力均减小，其中第4层减小最多。

由以上分析对比可知，方案二在随机地震动作用下顶层位移、各层层间位移和层间剪力均减小，并没有造成顶层位移和某些楼层的层间位移、层间剪力增大的现象，明显优于其他方案，同时阻尼器耗能与布置位置直接相关，同的布置方式可能造成结构新的薄弱层出现，从而使其的地震反应增大。

表 1 非减震结构与三种布置方案下的结构自振频率

5 结论

通过考虑地震的随机性，采用层间剪切模型，运用虚拟激励法对装有黏滞阻尼器结构的进行平稳响应分析。以1栋6层的剪切型钢筋混凝土框架结构作为算例，对比在最大层间位移处集中布置、循环布置、权数布置三种阻尼器方案布置，用MATLAB进行了算例分析。通过研究，可以得出以下结论：

5.1 考虑到地震具有随机性，采用随机地震动模型比确定的时程函数能更合理的描述地震随机性；同时虚拟激励法将平稳随机地震激励转化为简谐振动分析，是一种精确的分析方法。

5.2 黏滞阻尼器宜分散布置在层间位移较大的楼层及其相邻楼层，应避免集中布置在最大层间位移处，否则会造成结构的竖向刚度发生突变，使某些楼层成为新的薄弱层，增大这些楼层的地震反应。

5.3 附加黏滞阻尼器支撑能增加结构各阶振型的自振频率，同时减小各阶振型下的位移功率谱密度峰值。

[1]周云.黏滞阻尼结构减震设计[M].武汉：武汉理工大学出版社，2006.

[2]Soong.T；Song.T.T.Passive energy dissipation systems in structure engineering[M].1997.

[3]R H Zhang，T T Soong.SeismicDesign of Visco-elastic Dampers for Structural Application[J].Journal of Structural Engi⁃neering.1992，18（5）：1375-1392.

[4]李春祥，徐双正，张伏海等.复杂形体超高层钢框架-混凝土核心筒混合结构减震的研究[J].振动与冲击，2011（9）：184-190.

[5]王志强，胡世德，范立础.东海大桥黏滞阻尼器参数研究[J].中国公路学报，2005（3）：37-42.

[6]陈建斌，丁浩民.消能支撑方钢管混凝土高层建筑抗震设计[J].同济大学学报（自然科学版），2006，（11）：1431-1435.

[7]Bracci，J M Kelly，Lobo，et al.Seismic Retrofit of Rein⁃forced Concrete ructures Using Damping Devices[J].Base Isola⁃tion Passi-ve Energy Dissipation，and Active Control，1993（1）：216-228.

[8]D A Toutch.Seismic Retrofit of Nonductile Reinforced Concrete Frames Using Visco-elastic Dampers[J].Base Isolation，Passive nergy Dissipation，and Active Control，1993（1）：278-31 2.

[9]林家浩，张亚辉.随机振动的虚拟激励法[M].北京：科学出版社，2004.

[10]薛素铎，王雪生，曹资.基于新抗震规范的地震动随机模型参数研究[J].土木工程学报，2003（5）：5-10.

TB523

A

1671-0037（2014）10-76-2

赵子斌（1985.7-），男，硕士，助教，研究方向：结构抗震与减震控制。