随机共振技术的水声微弱信号提取算法

何世娜，胡晓毅

（厦门大学 信息科学与技术学院，水声通信与海洋信息技术教育部重点实验室，福建 厦门361005）

随机共振的概念是由邦济等［1－3］在研究古气象冰川问题上提出的，它是在一定的非线性条件下，由弱周期信号、噪声、非线性系统协同作用而导致的系统强周期输出的现象.该理论目前已广泛应用于生物、化学、光学等弱信号检测的研究中，以及雷达、声纳、图像处理和语音识别等通信领域的工作中.常规的弱信号处理方法都是采用线性滤波器，达到滤除带外噪声的作用，但对与信号同频带的带内噪声就束手无策了，特别是在宽带噪声的背景下，提取微弱信号就更困难.随机共振与传统检测算法的不同之处就在于它不是以尽可能的滤除噪声为目的，而是最大限度地利用噪声，通过非线性系统将噪声能量转化为信号能量，从而起到增强弱信号的效果.因此，它不存在带外还是带内的概念，这为我们实现水声信道中低信噪比环境下的信号检测提供了新的思路，将其应用于水声通信系统中可以克服传统滤波效果的局限性、信噪比瓶颈、功率受限等问题，进而降低检测成本，有很高的研究价值.通常情况下，水声信道的频段范围在2～30kHz左右，而受到绝热近似理论的条件限制，传统的随机共振只能应用于小于1Hz左右的小参数（低频）信号［4－5］，因此，必须采用大参数（高频）信号的随机共振法提取水声信号.目前，针对大参数的信号提取，研究人员相继提出了一些算法，主要有调制法、二次采样法、时域变换法和参数调节法［6－7］.前3种方法是从信号变换入手，核心思想是变频处理.调制法提取出的信号频点很准确，但前提是需知道信号的大致频率，而实际通信系统中，比如跳频系统，接收端并不知道该时刻的频点是什么，并且由于该算法会造成信号的幅度发散，收敛效果不好，对于非相干解调的系统而言会对系统性能产生一定的影响；二次采样对采样率有比较严格的要求，计算复杂度提升；时域变换的方法相对简单，但具体压缩倍数多少为最匹配并没有准确的定义.参数调节法是通过改变系统参数，使双稳态系统共振的频段往高频移动.参数变换法可以实现信号、系统之间的最佳匹配，但目前参数的选取还是靠经验值.本文结合参数变换和频域压缩变换法综合对信号进行处理，并通过水池实验，证实了该方法在水池环境、低信噪比下有很好的弱信号提取效果.该方法既保留了频域压缩变换的低复杂度又拥有参数变换法的最佳匹配度.

1 随机共振原理

受随机白噪声与外力作用的双稳态系统模型可以由Langevin方程表示，即

其中，x为系统输出，a、b为非线性双稳态系统的结构参数，二者为大于0的实数，该非线性双稳态系统的势函数可以表示为

其势阱图如图1所示.

式（1）和（2）表示单位质点同时受到外力和噪声驱动时，在双势阱中的过阻尼运动.可以看出，没有外力和噪声作用时，势垒高为势函数在x处取极小值，在x＝0处取极大值.当仅仅存在周期信号时，双稳态势阱在信号的驱动下随着信号频率f发生周期倾斜，相对势垒高度交替地升降，当信号的幅度（A）小于临界值时，质点只能在某个势阱中进行局部周期运动，具体哪个势阱由初始状态决定；当只有噪声作用时，质点在两个势阱间按Kramers跃迁率（rk）进行跃迁切换，rk取决于噪声分布和强度，表达式为

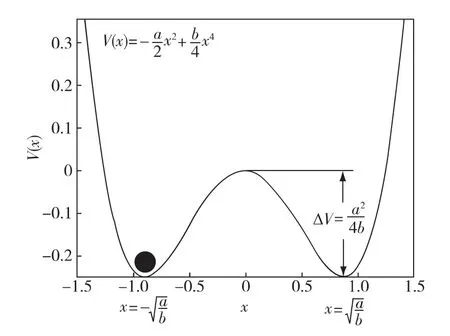
图1 当s（t）与Γ（t）均为0时，式（1）表示的双稳态势函数Fig.1 Potential function of the bistable system，when s（t）＝0，Γ（t）＝0in equation（1）

当系统受到弱信号和噪声同时作用时，周期信号给系统势阱的切换引入周期性变化，逐渐与噪声达成同步.当信号、噪声、系统非线性达到匹配时，即使此时信号幅度A小于AC，质点也可以在两个势阱间按信号频率f跃迁.换句话说，这里匹配的意思就是假设信号不变，当噪声强度由小变大时，系统的输出信噪比也随之由小增大，当达到一个峰值点（即最佳匹配）时，信噪比又由大到小减小，这类似于物理过程中的共振现象.

2 高频弱信号的随机共振

对于双稳态随机共振系统来说，实现共振必须满足3个条件［8］：1）信号本身并不足以推动系统越过势垒进入另一个状态；2）当信号与噪声混合后，有推动系统进入另外一个状态的可能，也就是说，噪声的大小要“足够”；3）信号频率、幅度、噪声都较小.由于粒子受阻尼作用的影响，描述非线性系统的郎之万方程随着信号频率的增大，达到共振所需的信号能量阙值增高，并且噪声通过双稳系统后呈现出能量向低频转移的现象，高频部分能量甚微，导致随机共振对于高频信号不敏感、难实现.为了解决这个问题，本文先通过尺度变换法将信号频率压缩到低频段，再通过改变系统参数使之达到最佳匹配.具体实现过程如下：

1）参数变换：参数b描述的是双稳态系统本身运动速度，本文统计出了b值相对于a值的最佳倍数与具体信噪比之间的关系.根据随机共振的条件，输入的周期信号的振幅A必须满足：A≤AC，AC为系统跃迁阙值；同时对于噪声来说，必须含有足够大的能量完成跃迁，即σ＞AC（其中σ是噪声的均方根值），所以发生随机共振必须满足A＜AC＜σ，实验过程中可以在信号没来前观测到噪声的幅度范围，根据输出信噪比的经验值估计出信号幅值，从而

同时，已经证明，双稳态系统随机共振数值仿真的必要条件为

2）时域变换：该部分有2种变换方式，假设信号为s（t）＝Asin（2πf0t），则式（1）写为

第1种变换：假设τ＝kt，则式（6）可以表示为

从式（7）可以看出，时间尺度变换相当于系统整体引入一个压缩系数k.

该种变换方法是在将系统的参数归一化，然后把变频的功能集中在信号幅度上，即归一化变换后相当于信号和噪声同时乘以比例因子当b＝a时，系统（8）相当于a＝b＝k的系统（7），本文将这2种方法结合，一方面根据信号真实频率选择适合的a来将信号归一化到想要的频点上，另一方面微调k进一步平滑信号，接着调节b使系统达到最佳匹配.

3）采样率和码元时宽的选取：根据奈奎斯特采样定律，采样率大于信号频率的2倍即可，但实际上［9］即使采样率达到信号的30多倍时，双稳系统还是会发散，采样率需达到信号频率的200倍时系统才有可能发生共振.对码元时宽而言，通过仿真结果显示，随机共振的效果随着码元时宽的增加而增大，但在现阶段的水声通信系统中，单载波非相干调制技术的最高可靠通信速率在200～400bits／s之间，因此，假设采用四进制码元，对应的最佳时长为即5～10ms之间，这里为了使双稳系统得到足够的能量，将时长选择为10ms.

3 水池实验

本文选用2kHz的高频单频点信号进行水池实验，验证了随机共振技术在水池环境条件下有很好的弱信号提取效果.信号参数为采样率：600kHz，总符号个数：10，单频信号频点：2kHz，码元长度：10ms，发送信号幅度：1V，同步信号频段：2～3kHz上调频，数据帧格式如表1所示.

从图2可以看出信号3和信号4已淹没在噪声中，从接收信噪比上看，这4组信号分别大概有7，5，1dB以及小于0dB左右.将该2组数据进行随机共振处理.根据a值为100倍信号频率这一经验值［9］，左右遍历寻找最佳性能a值，再循环搜索最佳匹配b值并压缩5倍的k值，共振前后信号的时域波形如图3～4.

这里将随机共振前的接收信号与本地信号相关，得到一个未经过随机共振处理的相关峰，记作before＿max，再将通过随机共振后的信号与本地信号相关，得到另一个相关峰，记作after＿max，暂且将这两个相关峰的差值叫做相关峰增益，即A＝after＿max－before＿max，由于相干解调的判决依据是相关峰的大小，自相关峰能量越大，判决准确度越高，从这个相关峰增益可以看出信号经过随机共振处理前后信号能量的变化情况.这里通过调整不同的系统参数a和b，得到了相关峰增益与a、b的关系，如图5所示.

从信号3和信号4的随机共振处理后信号的自相关峰值增益结果可得：随着信噪比的降低，随机共振的效果有所下降，在不同的系统参数下，自相关峰增益最大值由230降到110左右；信噪比一定的条件下，随着a的增大，系统性能逐渐增大，当a从700 000再继续增大时，增益趋于稳定；同时，a值一定的情况下，系统性能随着b值的增大呈现先增大后减小的趋势，且增益达到最大值时的b值随着信噪比的降低而增大，由信号3的70增大到信号4的110左右.

表1 数据帧格式Tab.1 Data frame format

time－domain waveform of single－frequency signal

图3 信号3随机共振前后时域波形Fig.3 Time－domain waveform of signal 3before and after processed by the stochastic resonance system

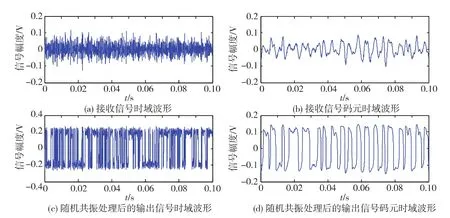
图4 信号4随机共振前后时域波形Fig.4 Time－domain waveform of signal 4before and after processed by the stochastic resonance system

图5 信号3与信号4在不同系统参数下随机共振后自相关峰值增益Fig.5 Autocorrelation peak－gain of signal 3and signal 4processed under different parameter of the stochastic resonance system

为了更明显地给出随机共振的效果，给出信号2和信号4随机共振处理前后相关峰的大小，这里需要说明的是，信号2和信号4在随机共振处理前后未做任何预处理.从图6可以看出，随机共振前，信号2的自相关峰值为316，信号4的自相关峰值为103，共振后信号4的自相关峰值为375，比信号2共振前的峰值还大，且信号2比信号4的发射功率大12dB，由此可见，随机共振技术有效地取得了一定的信噪比增益.

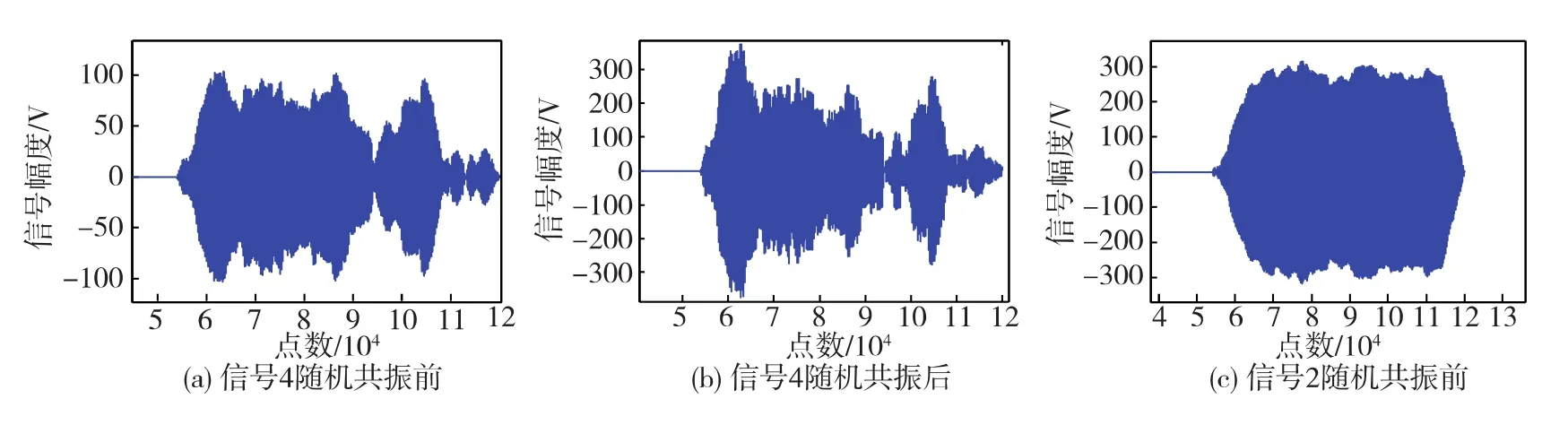
图6 信号4随机共振前、后与信号2随机共振前的自相关峰Fig.6 Autocorrelation peak－gain of signal 4before，after processed and signal 2 after processed by the stochastic resonance system

4 结 论

本文在传统小参数双稳态随机共振系统的基础上，结合尺度变换与参数调节2种方法，实现了单频点2kHz的高频弱信号的提取，并通过水池实验验证了该方法的有效性.然而在实际应用中还存在一些问题：首先是采样率的问题，实验过程中，采样率需高于信号频率200倍时系统才会收敛，随着信号本身频率的提升，采样率随之大幅度增大.如何降低系统的采样率是后续研究的课题.其次，关于特定频点所对应的最佳系统参数的选择目前仍是遍历的方法，最佳参数与频点之间的对应关系仍需进一步探讨研究.

［1］Benzi R，Sutera A，Vulpiani A.The mechanism of stochastic resonance［J］.J Phys A，1981，14（11）：453－457.

［2］McNamara B，Wiesenfeld K，Roy R.Observation of stochastic resonance in a ringLaser［J］.Physical Review Letters，1988，60：2626－2629.

［3］Collins J，Chow C C，Imhoff T T.A periodic stochastic sonance in excitable systems［J］.Physical Review E，1995，52（4）：R3321.

［4］李华锋，鲍荣浩，徐博候.应用随机共振进行海洋噪声背景下的信号检测［J］.浙江大学学报：工学版，2004，38（5）：640－643.

［5］薛力伟.随机共振系统的参数选取与应用研究［D］.兰州，兰州大学，2009.

［6］刘利姣，黄光明，杜茜，等.大参数随机共振的两种方法及数值仿真［J］.信息与电子工程，2007，5（3）：182－185.

［7］张良斌，张良英.调频随机共振实现大参数信号检测［J］.测控技术，2009，28（1）：89－91.

［8］高雯.基于非线性动力学原理的弱信号检测理论及提取方法研究［D］.北京：北京邮电大学，2009.

［9］胡茑庆.随机共振微弱特征信号检测理论与方法 ［M］.北京：国防工业出版社，2012.