WSN中基于贝叶斯压缩感知的信息隐藏传输研究*
2014-07-25熊继平宣利峰
熊继平,赵 健,宣利峰
(浙江师范大学 数理与信息工程学院 图形与图像处理研究所,浙江 金华 321004)
无线传感器网络[1]WSN(Wireless Sensor Network)是以数据为中心的网络,常被应用于军事、国防、物流、监测等领域,这些数据一旦被第三方恶意截获,将危及到全局WSN安全性,因此必须采取措施来保护WSN中的敏感数据。对称加密技术SET (Symmetric Encryption Technique)是目前广泛应用于WSN的安全方法之一[2],其特点是安全性较好,但所需的计算复杂度较高。由于WSN传感器节点安装的操作系统处理能力和电池能耗的限制条件,如果采用SET技术,那么整个WSN的生命周期将大大缩减。信息隐藏IH(Information Hiding)技术也是一种保障数据安全性的可靠方法。肖湘蓉等[3]第一次将信息隐藏技术与WSN结合起来,通过最低有效位算法将敏感信息嵌入到常规信息中,实现不被恶意感知的目的。但是该方法还存在两个问题:首先,在应用LSB算法前,敏感信息仍然需要通过对称加密方法进行加密;其次,对于无线信道的抗噪性较弱。
压缩感知[4-6]CS(Compressive Sensing)是一种信号处理领域新提出的技术,已在认知无线电、图像处理、计算机视觉、机器学习等诸多领域产生了深远的影响[7-10]。该理论表明,当信号满足稀疏性或者在某一变换域稀疏时,那么该信号能够通过少量测量值精确重构出来。CS编码简单的特点与WSN的网络结构高度契合,也即对传感器节点的编码要求非常低,目前利用CS实现数据的能量有效传输已经成为热门的研究方向[11-15]。Xiong Jiping等[16]首次将CS编码方案应用到无线传感器网络的敏感数据传输中,在无噪和丢包信道中能够很好地工作,但其在噪声信道中不能准确获得敏感数据。因此,本文针对无线信道中存在的噪声干扰问题,进一步提出一种基于贝叶斯压缩感知[17]BCS(Bayesian Compressive Sensing)的有噪信号重构算法,在降低编码端计算开销的同时实现数据的高效敏感传输和精确重构。
本文首先介绍贝叶斯压缩感知理论、随机贝叶斯重构方法及优化的自适应重构方法,然后将其引入无线传感器网络的敏感信息安全传输框架中,接着通过实验仿真验证方法的有效性,最后总结全文并指出下一步研究方向。
1 贝叶斯压缩感知理论
BCS理论就是从贝叶斯算法的角度来重构压缩测量值,实现信号传输的目的。假设原始信号 x(N×1)在某一组基B下是可压缩或者可稀疏的,则CS测量值可以表示为:

其中,Φ为传感矩阵,B为稀疏矩阵,ω为传输信号x在B的稀疏表示,y为测量矩阵。在BCS理论中,需要一个ω在某组基B上为稀疏的先验置信;y从压缩测量值观测获得,旨在为权值ω提供一个后验置信(密度函数)。贝叶斯框架在执行压缩测量时为加性噪声提供一个后验密度函数估计,因此,可以通过BCS解决信道噪声问题。
1.1 贝叶斯角度的压缩感知
假设噪声信号n由均值为0、方差σ2未知的高斯噪声近似构成,则可以得到:

由式(2)可以得到高斯似然模型为:
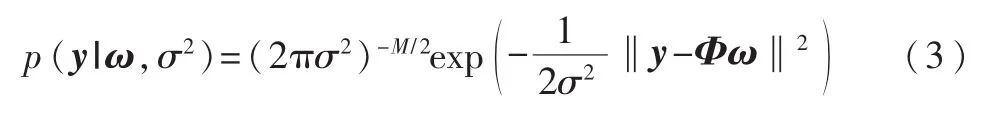
在贝叶斯公式中,通过在ω中放置稀疏促进先验获得其稀疏性。目前广泛采用的稀疏先验是拉普拉斯密度函数[18-19]:
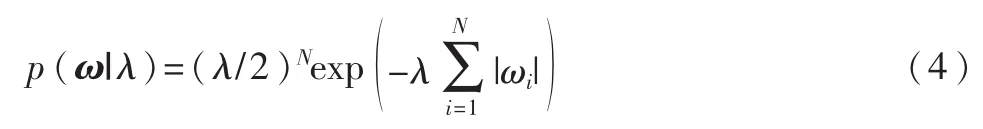
由于拉普拉斯先验与高斯似然不为共轭,直接采用拉普拉斯先验很难实现,因此,相关贝叶斯推理不会表现为闭型。通过构造分层先验构造拉普拉斯先验:
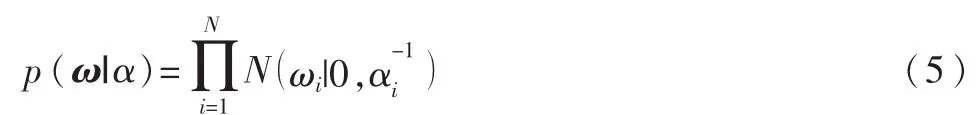
其中,αi是高斯密度函数的精度值。对超参数α赋Gamma先验:

其中,a和b是Gamma分布的两个参数。通过求解超参数α的边缘分布,全局先验ω通过式(5)和(6)估计获得:
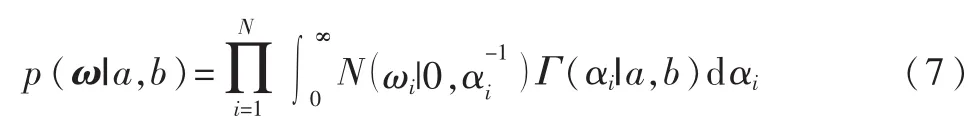
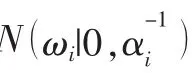
1.2 随机的贝叶斯CS重构
假定超参数α和α0=1/σ2已知,给定 CS测量值 y和投影矩阵Φ,后验ω服从多元高斯分布:
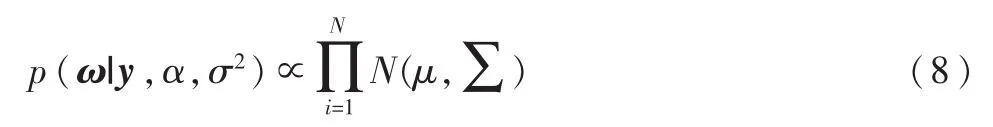
其中,均值和协方差分别为:

其中,A=diag (α1,α2, …,αN)。此问题亦为相关向量机(RVM)的学习问题,而此时相关向量机中相关的学习问题转换成了获取超参数α和α0=1/σ2。在 RVM中,这些超参数通过求解type-II最大似然获得的数据进行估计[20]。求解权值ω的边缘密度,α和α0边缘似等价于表示为对数 L(α,α0):
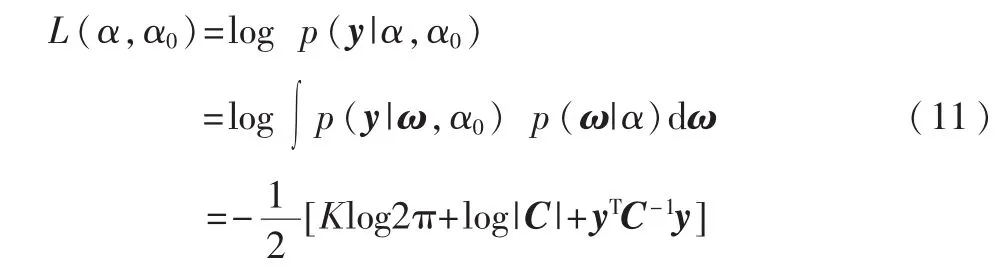
其中,C=σ2I+ΦA-1ΦT。采用α和α0点估计的 type-II最大似然近似法最大化式(9),能够通过 EM算法[21]实现并获得:
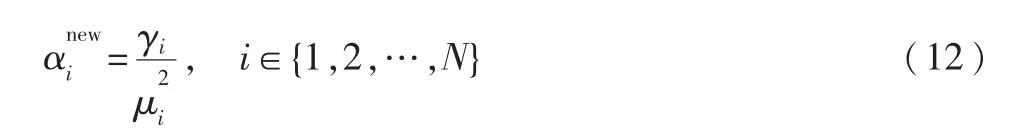
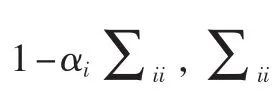
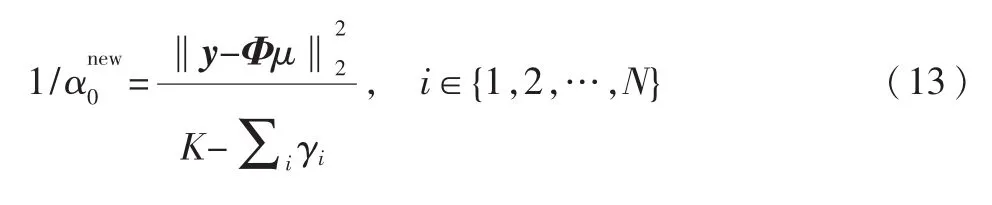
μ、Σ和α、α0可以交替进行迭代计算直到满足收敛条件。最后可以得到信号x=Bω后验密度函数也是一个多元高斯分布,均值和协方差为:

其中,协方差矩阵的对角元素产生一个x重构精度的误差条(Error Bars),以式(14)中均值的形式表示。
最近对RVM算法的理论分析[20-21]表明,RVM为l0范数稀疏性测量提供一个比l1范数更加紧的近似值,证明在最差的场景中,RVM也能优于其他广泛使用的稀疏表示算法。
1.3 优化的贝叶斯CS重构
在原始CS结构中,随机投影Φ由基本随机变量的独立同分布实现构成。此外,早期的文献用于估计ω的CS算法采用的是一个如式(16)的点估计方法:
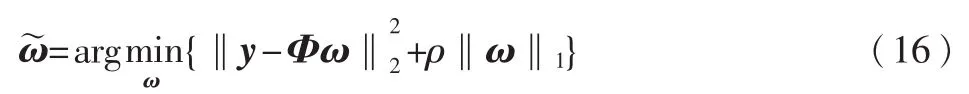
然而这些方法都没有考虑信号x的不确定性,因此Φ的自适应设计在这些方法中不适用。根据式(14)、(15)中定义,上一节中讨论的BCS算法能够实现对x的有效计算,因此考虑自适应随机投影rK+1的可行性来减少不确定性。该框架已经在实验设计及机器学习中被研究。
信号x的后验估计是一个均值E(x)=Bμ、协方差Cov(x)=BΣBT的多元高斯分布,因此x的微分熵(Differential entropy)满足:
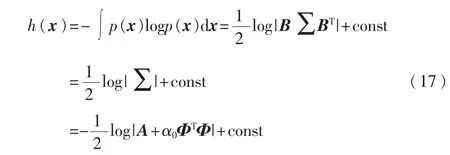
其中,常量 const独立于投影矩阵 Φ。由于A=diag(α1,α2,…,αN),因此 CS测量值y的微分熵独立性通过 α和α0的点估计定义。
在迭代过程中,选取最优新投影rK+1来最小化公式(17)中的微分熵。通过增加一个用rK+1表示且大小为(K+1)行向量来增广 Φ实现。用hnew(x)表示增加该新的投影向量Φ后的微分熵:
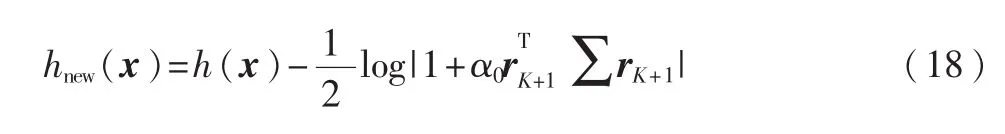
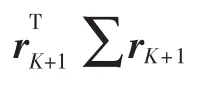
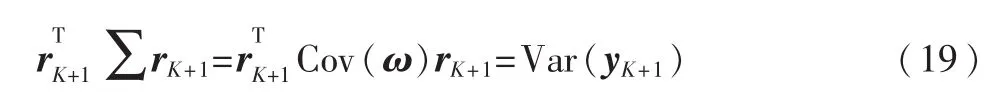
通过推导,式(19)等价于求预期测量值yK+1方差的最大值。换言之,投影rK+1应该被用于组成数据大多不确定的测量值yK+1,实现相关测量值的最大化利用。
本章提出自适应框架为新投影rK+1的选取提供一个较好的设置,在优化为目的情况中,x的不确定性将较大程度地减少。如果能够自适应地设计新投影rK+1,将执行一个矩阵的特征分解(Eigen Decomposition),并且被选作具有最大特征值的特征向量rK+1的表示。在随后仿真过程中,选取具有最大特征值的特征向量作为新投影rK+1。
2 基于BCS的WSN敏感信息传输模型
2.1 典型WSN
在一个典型的单跳WSN中,每一个节点都是通过无线信道与基站进行通信的。本文假设每个传感器节点都具有多传感器感知模块,能够同时采集不同的敏感信息和常规信息。在目标区域部署WSN前,设定各个传感器节点Ni与基站共享密钥Ki,各自存储在掉电不会丢失的存储区中。单跳WSN由部署在一定区域的传感器节点和基站组成,通过BS来采集各个节点的感知数据。单跳WSN的拓扑结构如图1所示。
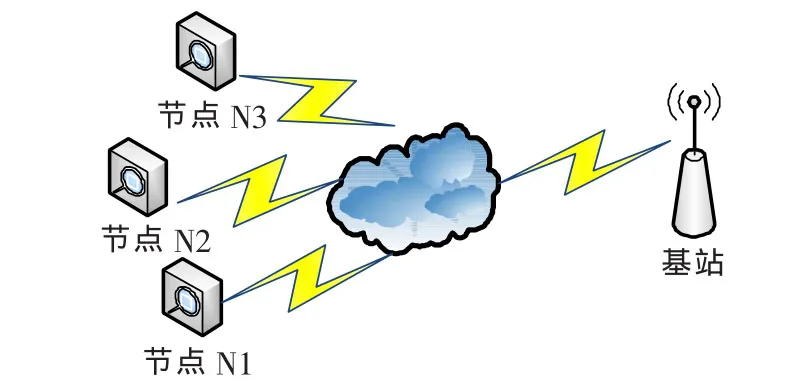
图1 单跳WSN的拓扑结构图
2.2 噪声信道数据敏感信息传输模型
建立一个基于BCS的单跳WSN敏感信息传输的模型,如图2所示。在传感器节点编码端,敏感数据通过BCS嵌入到常规载体数据中构成目标传输数据;目标传输数据通过具有噪声干扰的无线信道;在解码端,采用BCS解码算法重构敏感数据,利用向量作差和相乘获得常规载体数据,实现原始信号敏感的传输。
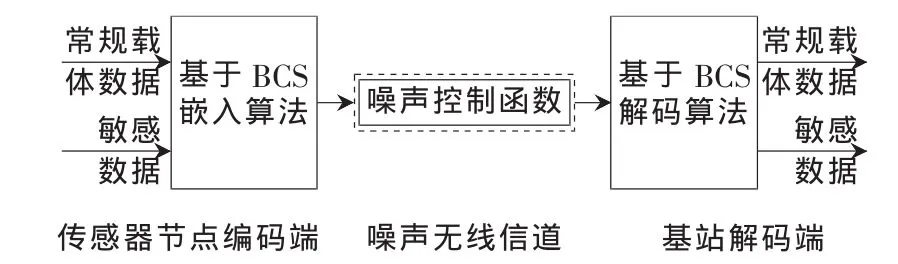
图2 基于BCS的有噪丢包数据安全敏感传输模型
本文采用的编解码算法流程如图3所示。
3 仿真结果及分析
3.1 基于随机BCS的噪声信道仿真结果与分析
为了验证提出方法的有效性,利用MATLAB模拟构建了一个噪声为n~N(0,σ2I)的无线信道。当传输数据通过无线信道时,利用噪声控制函数,模拟实现对数据的加噪控制。在解码端,分别采用凸优化算法、基追踪重构法和本文采用的随机BCS算法重构数据,通过比较体现BCS的优势。此外,本文还对BCS进行相应的改进,采用优化BCS方法对数据进行重构。
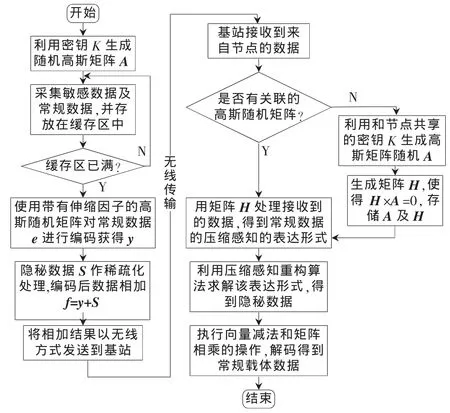
图3 无线传感器编解码端算法流程
敏感信息S的长度m=512,常规载体数据长度为n=256。ρ表示敏感信号S的稀疏率,ρ值越大,信号越不稀疏,传输的敏感数据越多,但重构所得到的数据效果越差。因此,通过仿真选取一个合适的ρ值,减少对重构效果影响的同时增加有效数据传输。常规载体数据e的长度为n=256,测量值的采样点个数k随着迭代次数而变化。投影矩阵 Φ由一个k×m的高斯分布N(0,1)矩阵构成,此处将Φ的行向量归一化到单位量级。噪声信号由均值为0、标准差为σ=0.005的高斯分布模拟产生。重构敏感信息衡量标准为均方误差、重构时间,其中,重构时间用t来表示,用于衡量算法的计算速度。
图4和表1分别给出了本文的仿真结果,其中,测量值采样点个数k=100,稀疏率ρ=5%。图 3(a)表示原始信号,图 3(b)、(c)、(d)分别表示 3 种方法的重构情况。由图可知,在噪声信道中,BCS重构在零点附近更加平滑,具有更好的去噪效果;而采用凸优化和基追踪[16]则包含较多毛刺信号,表明其无法消除重构数据中的噪声。此外,采用基本重构法和BP重构法会产生部分信号的丢失。从重构时间角度来看,采用贝叶斯压缩感知技术所需要的重构时间要小得多。
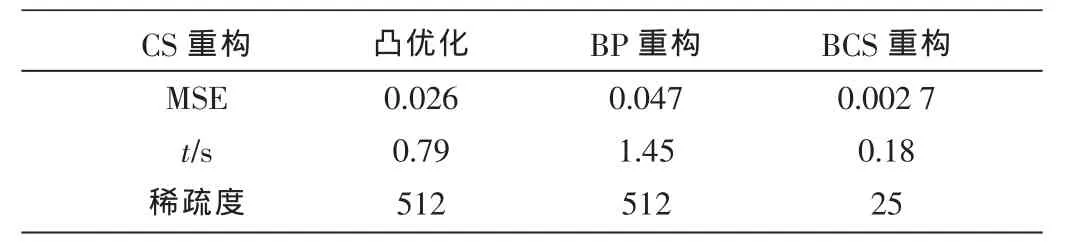
表1 噪声无线信道下3种不同CS重构算法比较(k=100)
3.2 基于优化BCS的噪声信道仿真结果与分析
图5给出了随机BCS方案和优化BCS方案的重构误差对比图。从中可以看出,优化BCS方法具备更好的性能,也即在相同的测量个数情况下,基于优化BCS的重构信号具有更高的信噪比。
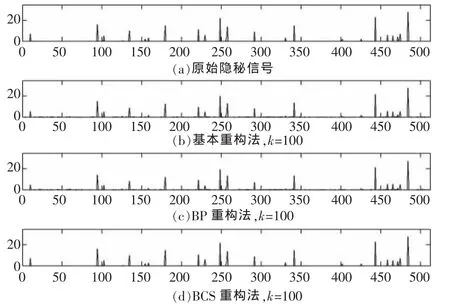
图4 噪声信道中3种重构效果对比(m=512,n=256,稀疏率ρ=5%)
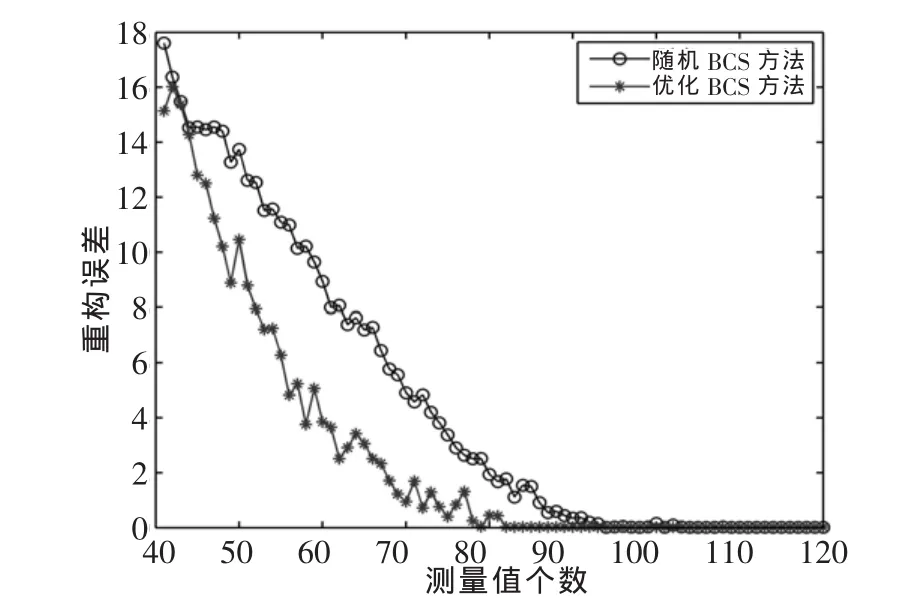
图5 噪声丢包信道中重构均方误差对比(m=512,n=256,稀疏率ρ=5%)
物联网应用的大面积推广和应用对数据的安全传输需求将会越来越迫切,本文研究了作为物联网网络基础的无线传感器网络中的敏感信息安全传输问题。提出了有噪信道下的基于贝叶斯压缩感知的敏感信息安全传输框架,并进行了模拟仿真。从仿真效果来看,本方案能够抵御一定的噪声,有效地恢复敏感数据和常规数据。
本文提出的信息隐藏方案本质上是在压缩感知域进行敏感信息的嵌入以及提取,明显不同于传统的基于空间域和频域的嵌入方案,因此在一定程度上可以促进信息隐藏技术的发展。此外,本文的关注点是敏感信息的有效嵌入和提取,对这种压缩感知框架下的信息隐藏技术进行隐秘性以及安全性等分析是今后研究的内容和主要方向。
[1]YICK J, MUKHERJEE B, DIPAK GHOSAL.Wireless sensornetwork survey[J].ComputerNetworks, 2008,52(12):2292-2330.
[2]ALI S T, SIVARAMAN V, DHAMDHERE A, et al.Secure key loss recovery fornetwork broadcastin single-hop wireless sensor networks[J].Ad Hoc Networks, 2010,8(6):668-679.
[3]Xiao Xiangrong, Sun Xingming, Yang Lincong, etal.Secure data transmission of wireless sensor network based on information hiding [C].Fourth AnnualInternational Conference on Mobile and Ubiquitous Systems, 2007: 1-6.
[4]DONOHO D L.Compressed sensing[J].IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[5]CANDÉS E, TAO T.Decoding by linear programming[J].IEEE Transaction on Information Theory, 2005, 51 (12):4203-4215.
[6]STROHMER T.Measure what should be measured:progress and challenges in compressive sensing[J].Signal Processing Letters, IEEE, 2012, 19(12): 887-893.
[7]Yi Yang.Perceptual compressive sensing for image signals[C].ICME, 2009: 89-92.
[8]Wang Ying, POLO Y L, PANDHARIPANDE A, et al.Distributed compressive wide-band spectrum sensing[C].Infornation Theory and Applications workshop, IEEE, 2009:178-183.
[9]KANG L W,LU C S.Distributed compressive video sensing[C].2009 IEEE International Conference on Acoustics, Speech,and Signal Processing, 2009:1169-1172.
[10]LUO C, WU F, SUN J, et al.Compressive data gathering for large-scale wireless sensor networks[C].Proceedings of the 15th Annual International Conference on Mobile Computing and Networking, ACM, 2009: 145-156.
[11]孙洪,张智林,余磊.从稀疏到结构化稀疏:贝叶斯方法[J].信号处理,2012,28(6):759-773.
[12]唐亮,周正,石磊,等.基于能量均衡的无线传感器网络压缩感知算法[J].电子与信息学报,2011,33(8):1919-1923.
[13]WANG J, TANG S, YIN B, et al.Data gathering in wireless sensornetworks through intelligentcompressive sensing[C].INFOCOM, 2012 Proceedings IEEE, 2012:603-611.
[14]SHEN Y, HU W, RANA R, etal.Nonuniform compressive sensing for heterogeneous wireless sensor networks[J].IEEE Sensors Journal, 2013, 13(6): 2120-2128.
[15]练秋生,刘芳,陈书贞.基于块A*正交匹配追踪的多传感器数据联合重构算法[J].电子与信息学报,2013,35(3):721-727.
[16]Xiong Jiping, Xuan Lifeng, HuangTao, etal.Novel covertdata channelin wireless sensornetworks using compressive sensing[J].Journal of Networks, 2012, 7(10):1523-1529.
[17]Ji Shihao, Xue Ya, LAWRENCE C.Bayesian compressive sensing[J].IEEE Transactions on Signal Processing, 2008,56(6): 2346-2356.
[18]TIPPING M E.Sparse Bayesian learning and the relevance vector machine[J].Journal of Machine Learning Research,2001(1): 211-244.
[19]GEORGE E I,MCCULLOCH R E.Approachesfor Bayesian variable selection[J].Statistica Sinica, 1997(7):339-373.
[20]WIPF D P,RAO B D.l0-norm minimization for basis selection [C].Advances in Neural Information Processing Systems (NIPS 17), 2005.
[21]WIPF D P,RAO B D.Comparing the effects of different weightdistributionson finding sparse representations[C].Advances in Neural Information Processing Systems(NIPS 18), 2006.
