可修复的表决系统的可靠性分析

方永锋,陈建军,曹鸿钧

(1.毕节学院机械工程学院,贵州毕节 551700; 2.西安电子科技大学电子装备结构设计教育部重点实验室,陕西西安 710071)

方永锋1,2,陈建军2,曹鸿钧2

(1.毕节学院机械工程学院,贵州毕节 551700; 2.西安电子科技大学电子装备结构设计教育部重点实验室,陕西西安 710071)

根据强度应力干涉理论,给出了kn表决系统的单元在多次随机作用下且单元抗力退化情况下的动态可靠性指标计算模型,由可靠性指标求得单元的动态失效概率.根据单元的动态失效概率,给出了在多次随机外部作用下,单元失效数目变化的概率,再由可修复kn系统所具有的马尔可夫性质,给出了在多次随机外部作用下的可修复kn系统的转移概率,由转移概率获得概率密度矩阵,通过求解微分方程组计算出系统的动态可靠度.最后通过算例说明该方法方便易行,计算结果符合工程实际.

随机作用;可修复;kn系统;动态;可靠性

笔者在相关文献的基础上,研究在多次随机作用下,可修复的kn表决系统配有一个维修工情况下的动态可靠性问题,建立该系统的动态可靠性预测模型,预测系统的可靠度随时间的变化规律.

1 多次随机作用下可修复的表决系统

在n个单元组成的系统中,若至少有k个单元同时正常的系统才能正常工作,此种系统即为kn表决系统.显然,当k=1时,该系统成为并联系统,而当k=n时成为串联系统.

随机外部作用m次时的等效作用smax的概率分布函数为

这里,G(smax)为smax的概率分布函数,其对应的概率密度函数为g(smax),smax的均值和均方差分别为μ(smax)和σ(smax).

通常随机外部作用的发生是服从参数为λLt的泊松(Possion)分布[9],由此可得在t时刻应力的概率为

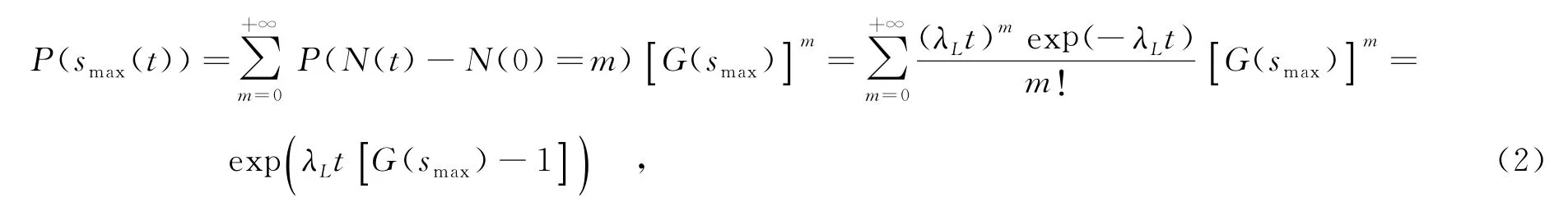
式中,N(t)为时段[0,t]内随机外部作用出现的总次数,N(0)为0初始时刻随机外部作用出现的次数,m为从0到t时刻随机外部作用发生的次数.

经式(2)的处理,随机作用次数m已被转化为时间.现将式(2)中的smax换为s,则式(2)可表示为

由代数综合法求得P(s)的均值μ(s)和均方差σ(s)分别为

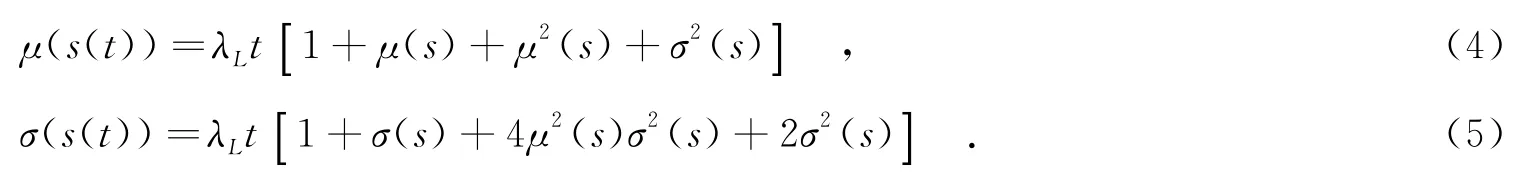
另外,考虑到系统中各工作单元的抗力r将是随作用次数增长而退化的随机变量,当作用t时刻后,系统中工作单元的剩余抗力r(t)为[14]

式中,r(0)是工作单元的初始抗力,T是单元的生命周期,s同式(3),c是材料指数.由式(6),可求得剩余抗力随机变量r(t)的均值和均方差分别为

式中,μ(r(0))、σ(r(0))为系统单元的抗力的初始的均值与均方差;μ(r(1))、σ(r(1))为系统单元的抗力被破坏时的均值与均方差,μ(r(1))=μ(s),σ(r(1))=σ(s),r(1)为工作单元的服役期满时的抗力.

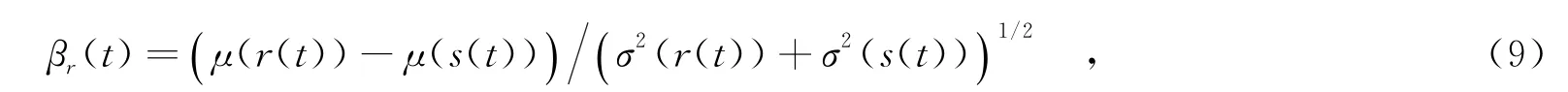
式中,Φ为标准正态分布函数.

记pij(Δτ)表示在Δτ时刻内系统由状态i转移到状态j的概率,即

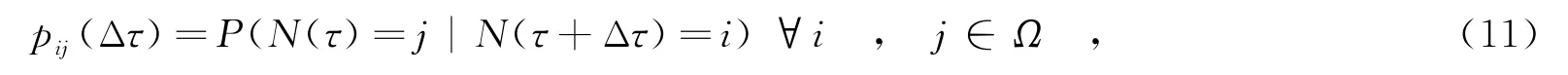
P(N(τ)=j|N(τ+Δτ)=i)表示由状态i转移到状态j的概率.

记aij表示t时刻一次外部作用之后系统中单元故障数量由i增加到j的概率,即

这里Pf=1-Rr(t).

利用以上关系,由转移状态可得系统的转移概率函数为

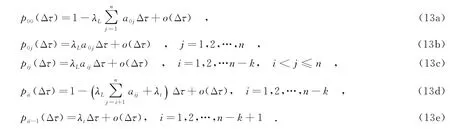
式中,o(Δτ)表示Δτ的高阶小量.

系统的概率密度矩阵中的元素为

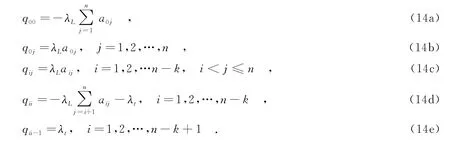
由马尔可夫链所具有的稳态分布性质,得到系统的稳态概率为

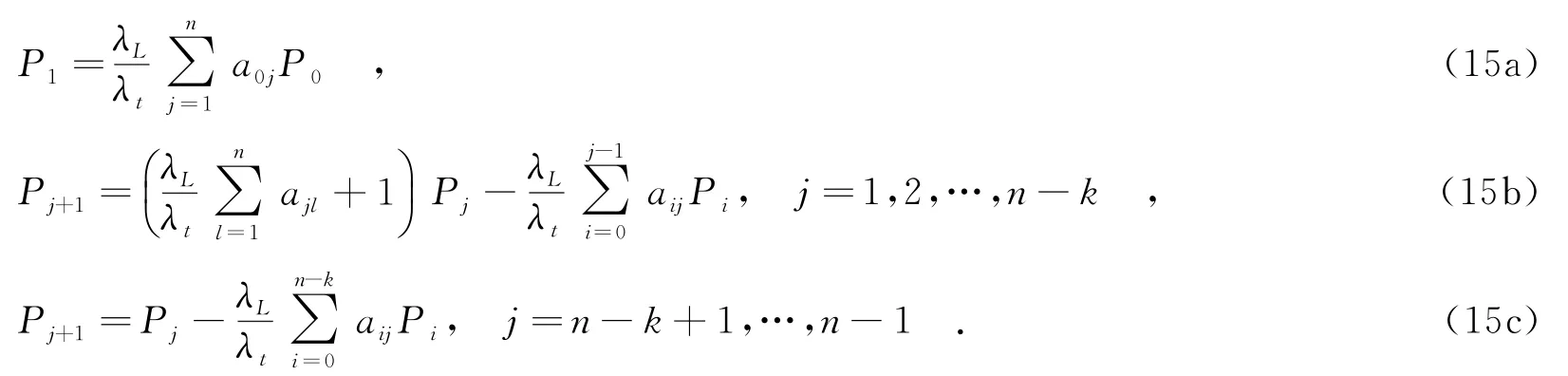
再由概率的完备性P0+P1+…+Pn=1进行回代,利用追赶法即可解出全部的稳态概率.

2 多次随机外部作用下可修复的表决系统的可靠性分析

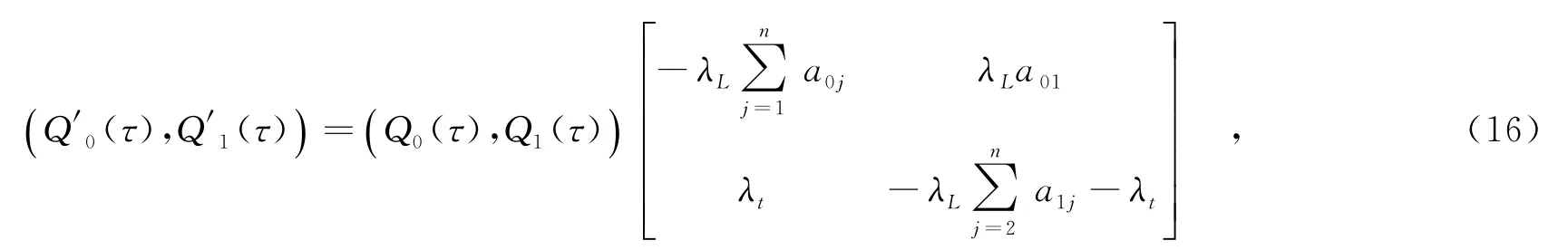
其初始条件为

由式(16)和式(17)求得Q0(τ),Q1(τ)分别为

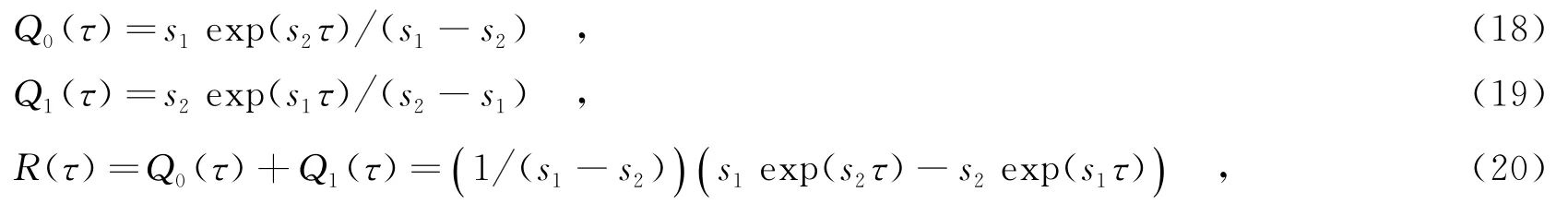
式中,s1,s2的表达式为

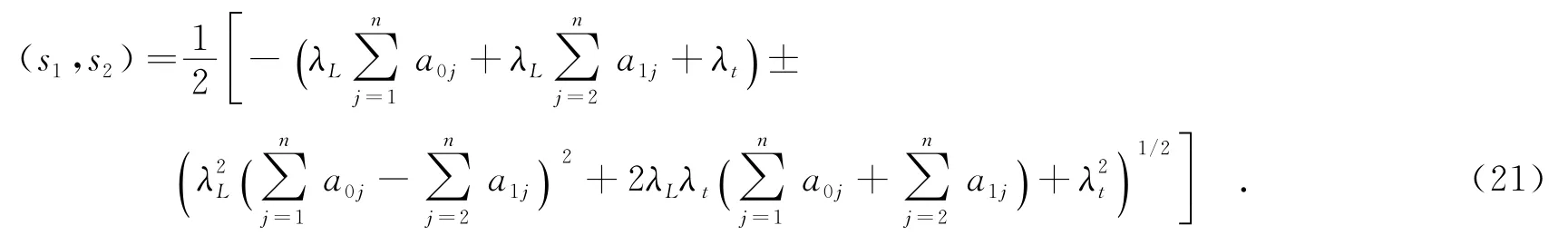
式(20)即为在多次随机外部作用下配有一个维修工的(n-1)/n表决系统动态可靠度预测的计算表达式.对于配有一个维修工的kn表决系统的可靠性预测分析过程亦基本类似.

3 算 例

这里以配有一个维修工的3/4表决系统为例,系统中各单元的初始抗力为r(0)～N(600,60)MPa,单元的工作寿命周期T=10 000 h,外部随机作用量的幅值为L～N(400,40)MPa,作用强度λL=1.5/h,修理时间参数λt=1,材料系数c=4.092.求该系统的动态可靠度.

对此系统,当1个单元失效时则就判定该系统失效.根据式(9)计算得到系统中工作单元的动态可靠性指标为

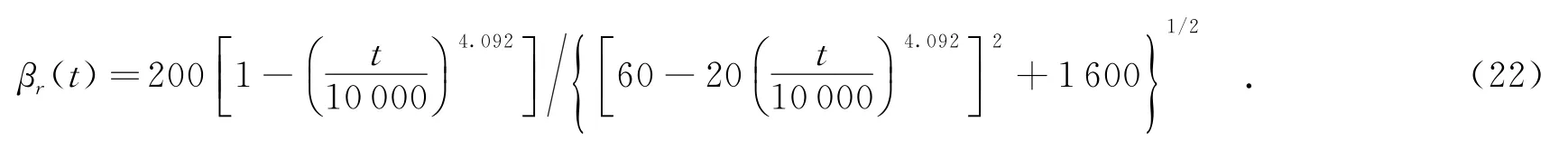
对式(22)的数值计算结果见图1.当外部作用于系统至t=6 528 h时,系统中工作单元的可靠性指标开始急速下降,表明系统工作单元失效的可能性将快速增加.因此,就用这一时刻的系统单元失效概率计算系统的aij.现将t=6 528 h代入式(22),得

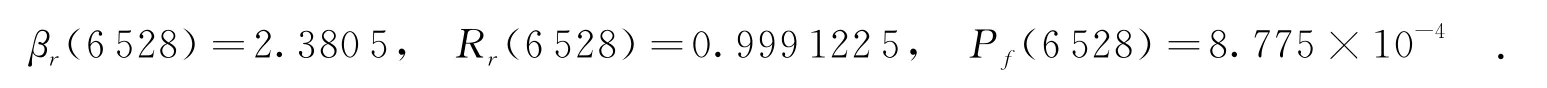
由式(12)计算得到

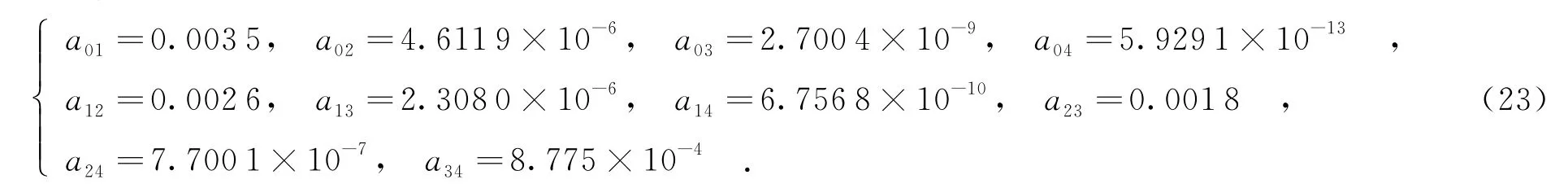
由式(23)求得系统的概率密度矩阵为

再由式(20)和式(24)解得系统的动态可靠度为

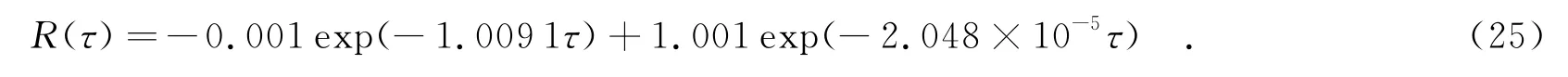
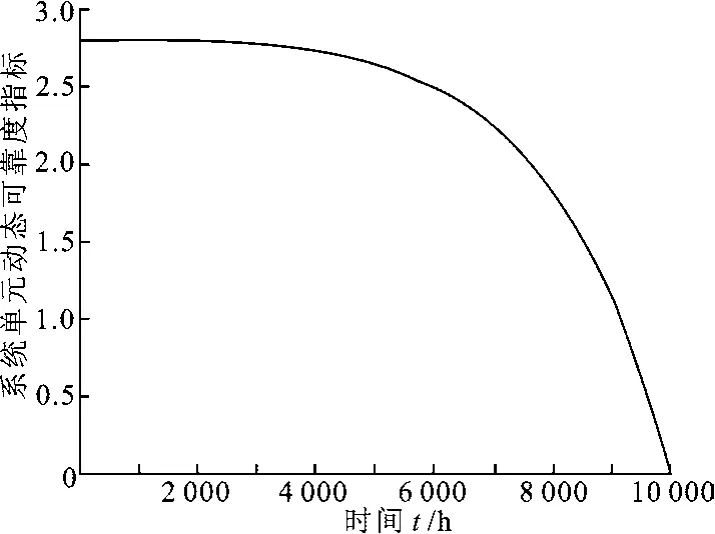
图1 3/4可修复系统单元动态可靠性指标

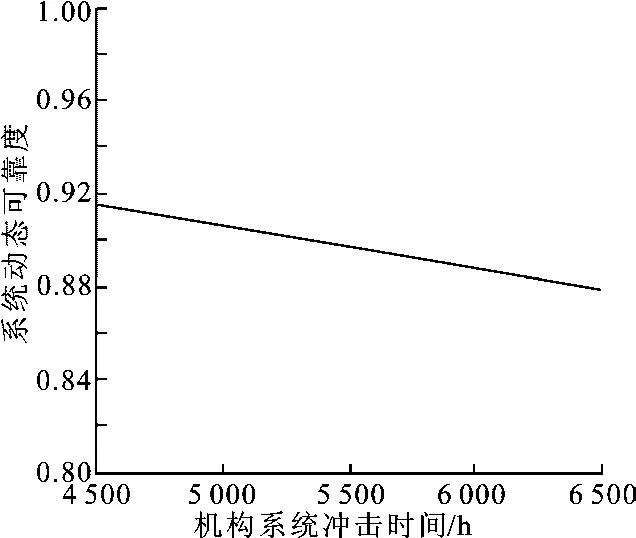
图2 3/4可修复系统的动态可靠度

对式(25)的数值计算结果见图2.分析式(25)和图2可以看出,当外部作用时间多于6 500 h之后,即系统服役到4 333.3 h之后,系统的可靠度下降至0.917 9.由于对该系统配有一个维修工,使从此时刻开始系统的可靠度相比前面的服役时刻下降有所减慢.当外部作用至10 000 h时,即系统服役到6 667 h时,系统的可靠度下降到0.876 0,已到了系统的服役期限.实际上,在系统的服役期限的时间节点之后,随着外部作用次数的增加,维修时间的延长,该系统的可靠度将还会再进一步以更快的速度下降,这些变化趋势与工程实际情况是完全相符的.

4 结束语

(1)笔者给出了系统单元的动态可靠性指标计算公式,通过该公式得到了多次外部随机作用下的配有一个维修工的kn表决系统的概率密度矩阵以及它的稳态分布计算模型,然后计算了多次外部随机作用下的配有一个维修工的(n-1)/n系统的动态可靠度模型.

(2)算例表明,文中方法建立的多次随机作用下配有一个维修工的kn表决系统动态可靠性预测模型在工程应用中方便可行,计算结果符合工程实际.

[1]张义民.任意分布参数的机械零件的可靠性灵敏度设计[J].机械工程学报,2004,40(8):100-105.

Zhang Yimin.Reliability Sensitivity Design for Mechanical Elements with Arbitrary Distribution Parameters[J].Chinese Journal of Mechanical Engineering,2004,40(8):100-105.

[2]Roy D,Dasgupta T.A Discretizing Approach for Evaluating Reliability of Complex Systems under Stress-strength Model [J].IEEE Transactions on Reliability,2001,50(2):145-150.

[3]Yao Chengyu,Zhao Jingyi.Reliability-based Design and Analysis on Hydraulic System for Synthetic Rubber Press[J]. Chinese Journal of Mechanical Engineering,2005,18(2):159-162.

[4]Sun Youchao,Shi Jun.Reliability Assessment of Entropy Method for System Consisted of Identical Exponential Units [J].Chinese Journal of Mechanical Engineering,2004,17(4):502-506.

[5]Krishnan R,Somasundaram S.Reliability Analysis of Repairable Consecutive-k-out-of-n:G Systems with Sensor and Repairmen[J].International Journal of Quality&Reliability Management,2011,28(8):894-908.

[6]Utkin L V.Reliability Models of m-out of-n System under Incomplete Information[J].Computer and Operation Research.2004,31(10):1681-1702.

[7]Xie Liyang,Zhou Jinyu,Hao Changzhong.System-level Load-strength Interference Based Reliability Modeling of k-outof-n System[J].Reliability Engineering and System Safety,2004,84(3):311-317.

[8]王正,康锐,谢里阳.以载荷作用次数为寿命指标的失效相关系统可靠性建模[J].机械工程学报,2010,46(6):188-194.

Wang Zheng,Kang Rui,Xie Liyang.Reliability Modeling of Systems with Depaendent Failure When the Life Measured by the Number Of Loading[J].Journal of Mechanical Engineering,2010,46(6):188-194.

[9]方永锋,陈建军,阎彬,等.结构动态非概率可靠性预测模型[J].西安电子科技大学学报,2012,39(6):170-175. Fang Yongfeng,Chen Jianjun,Yan Bin,et al.Model for Prediction of Structural Dynamic Non-probabilistic Reliability [J].Journal of Xidian University,2012,39(6):170-175.

[10]Lewis E E.A Load-capacity Interference Model for Common-mode Failures in 1-out-of-2:G Systems[J].IEEE Transactions on Reliability,2001,50(1):47-51.

[11]聂涛,盛文.K/N系统可修复备件两级供应保障优化研究[J].系统工程与电子技术,2010,32(7):1452-1457. Nie Tao,Sheng Wen.Research on Two Echelon Supply Support Optimizing for Repairable Spare Parts of K/N System [J].Systems Engineering and Electronics,2010,32(7):1452-1457.

[12]Xu Houbao,Guo Weihui,Yu Jingyuan,et al.Asymptotic Stability of k-out-of n:G Redundant System[J].Acta Analysis Fanctionalis Applicata,2004,6(3):209-219.

[13]杨莹,李俊民,陈国培.一类广义混杂系统的随机稳定性及稳定化[J].西安电子科技大学学报,2010,37(5):866-871. Yang Ying,Li Junmin,Chen Guopei.Stochastic Stability and Stabilization for a Class of Singular Hybrid Systems[J]. Journal of Xidian University,2010,37(5):866-871.

[14]Schaff J R,Davidson B D.Life Prediction Methodology for Composite Structures[J].Journal of Composite Materials, 1997,31(2):127-157.

(编辑:王 瑞)

Analysis of dynamic reliability of the repairable k-out-of-n system under several times random shocks

FANG Yongfeng1,2,CHEN Jianjun2,CAO Hongjun2
(1.School of Mechanical Engineering,Bijie University,Bijie 551700,China;2.Ministry of Education Key Lab.of Electronic Equipment Structure,Xidian Univ.,Xi’an 710071,China)

The model of unit dynamic reliability of the reparable k-out-of-n system is given under several times random shocks with the strength of unit degradation according to the strength-stress theory and the unit failure probability can be observed by using the dynamic reliability.The unit failure number can be obtained under several times random shocks according to the unit failure probability.The conversion probability of the reparable k-out-ofn system is given by its Markov property under several random shocks.The probability density matrix is observed by the conversion probability,and then the dynamic reliability of the reparable k-out-of-n system is obtained by solving the differential equation systems.Finally,it is illustrated that the method is prachcable and convenient. The calculated result conforms to the engineering practice.

random shock;reparable;k-out-of-n system;dynamic;reliability

TH122

A

1001-2400(2014)05-0180-05

2013-05-16< class="emphasis_bold">网络出版时间:

时间:2014-01-12

国家自然科学基金资助项目(50905134);中央高校基本科研基金资助项目(JY10000904012)

方永锋(1975-),男,副教授,博士,E-mail:fangyf_9707@126.com.

http://www.cnki.net/kcms/doi/10.3969/j.issn.1001-2400.2014.05.030.html

10.3969/j.issn.1001-2400.2014.05.030