重载铁路桥上无缝线路断缝允许值的研究

李 敏 高 亮 谷呈朋

(1.中铁工程设计咨询集团有限公司， 北京 100055； 2.北京交通大学 ， 北京 100044)

重载铁路桥上无缝线路断缝允许值的研究

李 敏1高 亮2谷呈朋1

(1.中铁工程设计咨询集团有限公司， 北京 100055； 2.北京交通大学 ， 北京 100044)

钢轨的断缝检算是无缝线路结构设计的内容之一，桥上无缝线路的断缝值与桥上扣件的布置形式及线路纵向阻力取值有关。基于有限元软件ABAQUS建立了不同断缝值的桥上无缝线路静力学与动力学计算模型，分析了不同断缝位置和30 t轴重条件下对货物列车通过断缝时钢轨的位移和受力等力学特性以及脱轨系数等动力响应评价指标的影响。计算结果表明，重载铁路桥上无缝线路设计中断缝值应采用70 mm。

重载铁路 桥上无缝线路 断缝允许值 30 t轴重

1 研究背景

钢轨的断缝检算是无缝线路结构设计的内容之一，桥上无缝线路的断缝值与桥上扣件的布置形式及线路纵向阻力有关。重载铁路由于列车轴重大，速度相对低，与高速铁路对轨道平顺性、舒适度等要求有着较大的区别。

铁科院曾在北京环形试验基地有砟轨道地段进行了列车通过钢轨断缝的安全试验，试验线路采用50 kg/m钢轨、木枕、有砟道床。在一股钢轨设置断缝，其大小由20 mm、60 mm、100 mm 逐次扩大，最终设置断缝138 mm。为保证试验安全，用2 辆轴重210 kN货物车辆溜放通过，车辆通过断缝速度，从20 km/h、40 km/h 逐次提高，最终达到85 km/h。通过试验测定顺车轨与迎车轨形成的台阶，顺车轨所受垂向力P、横向力H，顺车轨的弹性挤开量δ，迎车轨所受横向力、挠度等6项参数。

根据本次试验研究，确定我国铁路有砟轨道无缝线路钢轨断缝允许值为：一般情况可取70 mm；在满足一定条件下，断缝允许值取90 mm。

2 研究内容

2.1 研究思路

主要通过模拟列车车轮通过断缝处的轮轨力、脱轨系数、轮对横向力等方面进行分析。为简化模型，轨下基础采用弹簧叠加之后的刚度代替。其中，静力学着重研究重载列车对不同断缝位置的冲击影响，考虑断缝位于沿线路纵向两个相邻扣件的中央与扣件边缘两种工况，模拟重载列车通过不同长度断缝时的变形与受力。

综合静力学分析得到列车通过断缝时最不利位置后，进行列车通过最不利断缝处的动力学分析，基于不同轴重重载列车通过不同长度断缝的动力仿真研究，为我国重载铁路桥上无缝线路断缝值的取值提供参考。

2.2 模型计算参数

钢轨采用CHN60断面，断面积A=77.45 cm2，质量M=60.64 kg/m，水平轴惯性距为3 217 cm4，竖直轴惯性距为524 cm4。材料参数为：弹性模量E=2.06×1011N/m2，泊松比μ=0.3，密度ρ=7.8×103kg/m3。扣件采用弹簧和阻尼单元模拟，间距取为600 mm。

重载列车有限元模型主要包含轮对等要素，计算参数参考我国C80参数，轮对踏面采用LM磨耗型踏面，轮载冲击系数取3.0。

3 静力学分析

3.1 静力学分析模型

基于上述参数条件，建立静力学有限元分析模型。

(1)为分析钢轨在一节车厢静载下的变形及消除边界条件的影响，模型中钢轨长度取50 m(转向架中心距定为10.15 m，固定轴距2.6 m)。钢轨采用实体单元，模型中考虑设立1∶40的轨底坡。

为重点分析断缝处的变形和受力情况，断缝处单元沿纵向长度取50 mm，远离断缝处的网格长度逐渐变大。模拟断缝处的局部网格如图1所示。

(2)扣件及轨下基础分别简化为具有纵、横、垂向刚度的弹簧阻尼单元，扣件间距取600 mm。

(3)静力学分析考虑轮子和钢轨之间的接触，轮子受静载450 kN。计算分3步进行，第一步为轮子和钢轨的接触，第二步为轮子受450 kN载荷，第三步为在受载同时轮子向迎车轨方向移动。静力学分析模型如图1所示。

图1 断缝处静力有限元分析模型

3.2 静力学计算结果示例

静力学计算中分别考虑以下两种工况：工况一，断缝位于沿线路纵向两个相邻扣件的中央；工况二，断缝位于扣件边缘。断缝值考虑70 mm、80 mm、90 mm、100 mm和110 mm等五种情况。

以迎车轨条件为例，给出六种不同断缝值条件下两种工况的钢轨的最大垂向位移、最大横向位移、最大Mises应力和最大接触应力的对比(如图2至图5所示)。

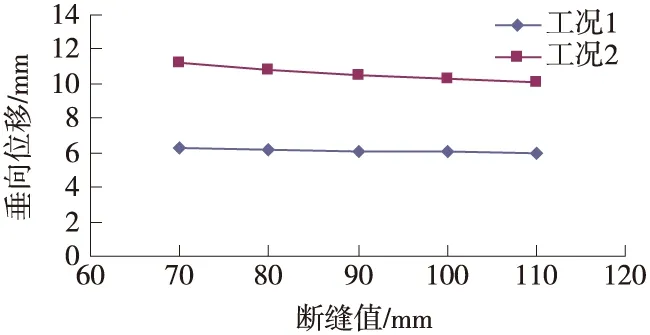
图2 不同工况迎车轨最大垂向位移对比

图3 不同工况迎车轨最大横向位移对比

图4 不同工况迎车轨最大Mises应力对比

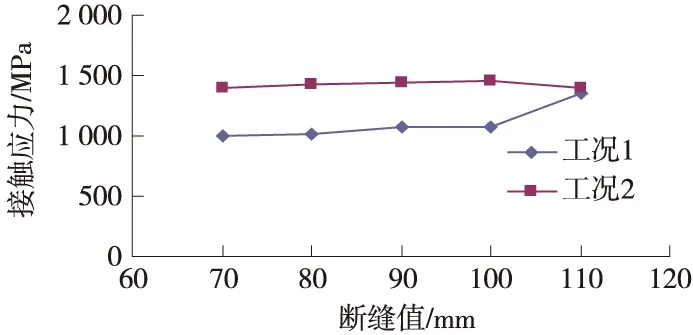
图5 不同工况迎车轨最大接触应力对比

3.3 静力学分析小结

通过30 t轴重条件下对不同断缝位置、不同断缝值条件下顺车轨和迎车轨的垂向和横向位移、Mises应力及接触应力进行了分析计算，得到结论如下：

①断缝位置对列车安全通过断缝具有重要影响，当断缝位于扣件边缘时较断缝位于扣件中间时显然更不安全。

②断缝值为100 mm时，钢轨的接触应力有明显增加，但受扣件处约束作用垂横向位移相较有所降低。桥上无缝线路断缝值的允许值设置为70～90 mm均是合理的。

③考虑到静力学模型的局限性，无法体现出重载列车车轮通过断缝处钢轨的瞬态冲击力，仅能反映列车通过不同位置断缝时对钢轨变形与受力的影响，有必要建立动力仿真模型，重点分析研究不同速度条件下，不同轴重车辆通过不同断缝时的冲击影响。

4 动力学分析

4.1 动力学分析模型

动力学仿真模型主要分为钢轨、扣件、轨下基础和车辆模型等几个要素，钢轨和扣件的模拟与静力分析模型一致。

对于车辆模型中车体、转向架和轮对三大构件，运动主要为刚体运动，不考虑其内部应力分布情况，假定车体、转向架和轮对都是刚体；对于车体和转向架、车轮和转向架之间均通过弹簧阻尼单元连接并发生相互作用。

转向架结构中的中央悬挂模型提供三个方向刚度和阻尼，由横向减振器提供中央横向阻尼。轴箱悬挂模型包括由轴箱弹簧提供的三个方向上的刚度，一系的垂向阻尼由悬挂在轴箱定位弹簧外侧的一系垂向减振器提供。以上的弹簧、阻尼均以刚度和阻尼元件一并予以考虑。

根据以上的车体模型、转向架模型和轮对模型，以及一系、二系弹簧和阻尼情况，建立的有限元动力学模型如图6和图7所示。

图6 动力学仿真模型

图7 动力学模型局部放大

4.2 动力学计算结果汇总

评判重载列车通过断缝是否会出现脱轨，各项指标如轮轨垂向作用力、横向作用力是否会出现超限的主要标准包括：脱轨系数Q/P≤0.8、轮对横向水平力Q≤80 kN、脱轨系数超限时间≤15 ms。

基于静力学分析结果得到：当断缝位于扣件边缘时更不利列车安全通过；断缝在60 mm以下时，列车车轮比较容易跨过断缝。因此动力学分析将在上述结论基础上进行，分别得到了30 t轴重列车速度从80 km/h、100 km/h增加到120 km/h，通过不同断缝值时的轮轨力、脱轨系数、垂向位移、Mises应力和接触应力等的时程曲线，计算结果如表1～表4所示。

表1断缝值70 mm轮轨垂横向力、脱轨系数等仿真计算结果

速度/(km/h)垂向力P1/kN垂向力P2/kN横向力Q/kN脱轨系数Q/P脱轨系数超限时间/ms8040222452.70.1531.110041227656.70.1551.212044022264.40.2067

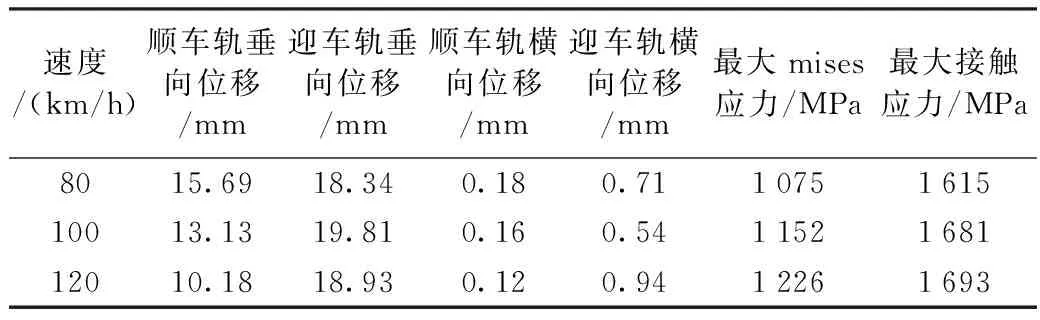
表2 断缝值70 mm轮轨垂横向位移、最大mises应力等仿真计算结果

表3断缝值90 mm轮轨垂横向力、脱轨系数等仿真计算结果

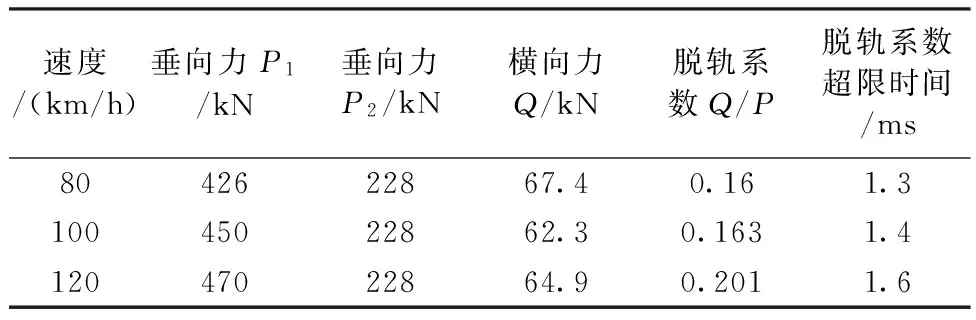
速度/(km/h)垂向力P1/kN垂向力P2/kN横向力Q/kN脱轨系数Q/P脱轨系数超限时间/ms8042622867.40.161.310045022862.30.1631.412047022864.90.2011.6

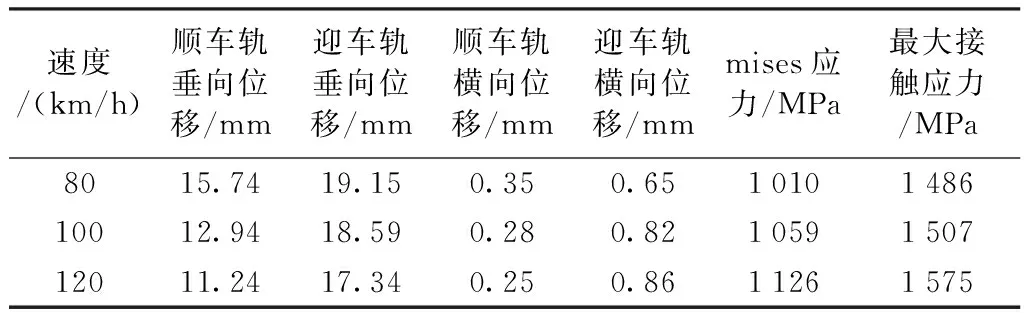
表4 断缝值90 mm轮轨垂横向位移、最大mises应力等仿真计算结果表

4.3 动力学分析小结

基于30 t轴重及本文所列参数条件下，得到如下结论：

①重载列车以80 km/h、100 km/h、120 km/h通过不同断缝值时，轮轨力、钢轨最大垂向力等增加较小，列车以不同速度通过断缝时的轮轨力变化、接触应力等时程变化趋势大致相同。轮轨冲击断缝后，均出现较为频繁的持续冲击，冲击时间间隔较短，前一次冲击响应尚未衰减完成，接着又叠加新一轮的冲击。

②断缝值从70 mm增加到90 mm时，发现90 mm断缝时其各项指标均在安全限度以内。但大于90 mm时，轮轨横向力等均在安全限值以内，但轮轨脱离时间较大，最多可到12 ms，较为接近限值15 ms。

③基于本文参数条件，从有限元计算结果来看，30 t轴重条件下，桥上无缝线路设计检算时最大断缝检算可设置为90 mm。

5 结论及建议

基于本文中的各项参数条件，综合列车通过断缝时的静力及动力计算结果，可以得到如下结论：

①当断缝小于90 mm时，列车速度小于120 km/h时都可以安全通过，基于此认为30 t轴重条件下，目前桥上无缝线路检算时断缝值取为70 mm是偏于安全的。

②从运营实践来看，由于断轨时的轨温一般高于设计所采用的历年最低轨温，实际断缝值小于设计计算值。对于大跨度桥梁，且气温变化较大的地区，设置小阻力扣件有可能出现断缝值大于70 mm的情况，该种情况应设置钢轨伸缩调节器。但钢轨伸缩调节器由于其固有的结构特性，尖轨断面有不同程度的削弱，其尖轨、基本轨接头是最薄弱的环节，若布置于桥梁横梁、桥台胸墙和支座中心等地段，在轮轨动力作用下，将导致病害增多，甚至折断。重载铁路上应慎用伸缩调节器，建议在该种条件下，桥上无缝线路的断缝检算值应设置为90 mm。

[1] 温泽峰，金学松，张卫华.钢轨轨缝接触-冲击的有限元分析[J].摩擦学学报，2003，23(3):240-243

[2] 刘彦普，谷爱军.钢轨接头轨缝值和行车速度对轮轨垂向振动的影响[J].中国安全科学学报，2005，15(11):82-86

[3] 赵文礼，张红兵.轮对在轨缝冲击力作用下的响应分析[J].兰州铁道学院学报，1999，1(18):51-54

[4] 许实儒.关于轮轨冲击力P1计算问题的探讨[J].兰州铁道学院学报，1992，4(11):1-9

[5] 卢耀荣.中国与欧洲桥上无缝线路设计理念的差异[J].铁道建筑，2006(1)

[6] TB10015—2012铁路无缝线路设计规范[S]

[7] 蒋金洲，卢耀荣.客运专线钢轨断缝允许值研究[J].中国铁道科学，2007，28(6)：25-29．

ResearchontheAllowableWidthofRailBrokenGapsofCWRonBridgeinHighSpeedRailway

LI Min1GAO Liang2GU Chengpeng1

2013-11-21

李 敏(1982—)，女，2008年毕业于北京交通大学土木建筑工程学院道路与铁道工程专业，工学硕士，工程师，E-mail：jerry.lmin@gmail.com。

1672-7479(2014)01-0110-04

U211.4；U213.42

： A