基于迁移矩阵法的锥柱结合壳固有振动特性分析

关珊珊，曹为午，谢官模

(1.武汉第二船舶设计研究所，湖北 武汉 430064； 2.武汉理工大学，湖北 武汉 430070)

基于迁移矩阵法的锥柱结合壳固有振动特性分析

关珊珊1，曹为午1，谢官模2

(1.武汉第二船舶设计研究所，湖北 武汉 430064； 2.武汉理工大学，湖北 武汉 430070)

基于迁移矩阵法给出了圆柱壳、圆锥壳以及锥柱结合壳的运动矩阵方程，给出了精细积分以及Runge-Kutta-Gill法的矩阵方程求解方法，大幅提高了求解精度及效率。进一步以不同边界条件下圆柱壳、圆锥壳和锥柱结合壳为算例讨论了锥柱耦合后圆柱壳及圆锥壳自身振动频率的变化。算例结果与有限元软件Ansys对比，验证了本文矩阵方程及求解方法的可靠性。

锥柱结合壳；迁移矩阵法；精细积分；固有振动特性

0 引 言

锥柱结合壳通常应用于潜艇、飞机、导弹以及水下自航潜器(AUVS)。锥柱结合壳体耦合振动的研究相关报道较少，早期的解析研究及试验工作主要采用有限元方法进行锥柱结合壳的固有频率及模态振型求解。Kalnins和Rose应用经典弯曲理论研究了旋转对称壳体。Hu和Raney研究了锥柱结合壳连接处不连续性的影响。Efraim和Eisenberger给出了级数解来计算分段轴对称壳体的固有频率。Patel采用有限元方法给出了含层状合成物的锥柱结合壳结果[1-5]。

Tottenham 和Shimizu[1]提出分析圆柱壳自由振动的传递矩阵法(或称传递函数法)。壳模型的传递矩阵法与普通的Timoshenko梁模型的传递矩阵法相比，具有以下优点：截面状态矢量的元素多，能考虑轴向变形与弯曲变形的耦合效应，结果更准确。通过场传递矩阵和点传递矩阵，建立起点和重点状态矢量的简便关系，在自由振动情况下，利用两端的边界条件得到系统的频率方程，从而求出结构的固有频率和模态；在强迫振动情况下，利用两端的边界条件得到两端状态矢量的未知元素，再利用各个传递矩阵逐步得到各个截面的状态矢量，得到系统动力响应特性。这种方法的关键是在传递矩阵的求解效率和精度上，其中精度主要受单元传递矩阵计算精度、传递矩阵连乘过程中的累积误差以及计算机的舍入或截断误差等的影响。Irite[6]采用传递矩阵法研究了锥柱结合壳的自由振动，其解法中是将传递矩阵用幂级数展开形式去逼近，在求解精度以及效率上均有较大限制。黄玉盈[7]进行了变厚度圆柱蓄水池动力分析。本文基于传递矩阵法推导了柱壳、锥壳以及锥柱结合壳的迁移矩阵运动学方程并采用精细积分和Runge-Kutta-Gill方法进行固有振动特性求解。算例计算结果与有限元软件Ansys获得的结果进行了对比，验证了本文方法的可靠性。

1 基本理论和分析方法

锥柱结合壳示意图如图1所示，采用如图所示的坐标系。

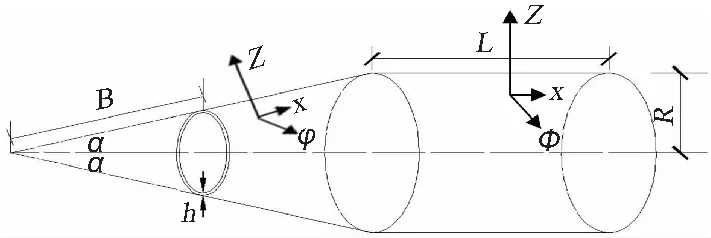
图1 锥柱结合壳示意图Fig.1 Sketch map of a coupled cylindrical-conical shell

1.1 圆柱壳自由振动传递矩阵

1.1.1 圆柱壳自由振动传递矩阵

惯性力引起的分布荷载为：

(1)

其中u,v,w分别为圆柱壳中面任一点沿母线、切线和径向的位移，ω的下标n均省略不写；公共的时间因子eiωt也略去不写。根据Flügge壳体理论，平衡方程为：

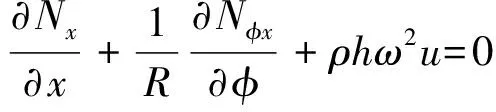
式中：ρ为材料密度；h为壳体厚度；ω为圆频率。

Kelvin-Kirchhoff剪力、膜力及所有内力分别为：

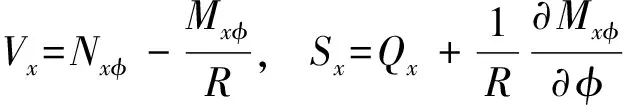
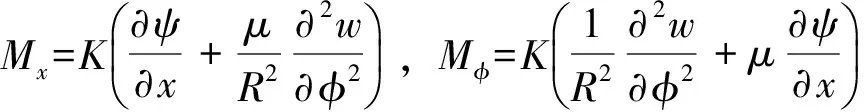
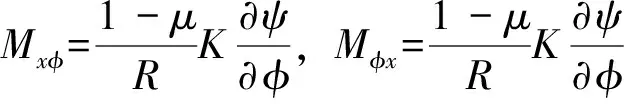
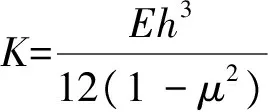
为简化分析，引进下列无量纲化的变量：

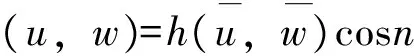
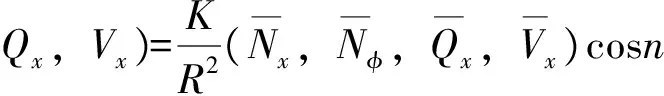
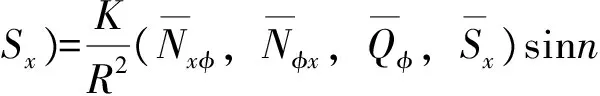
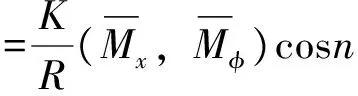
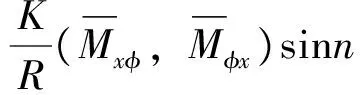
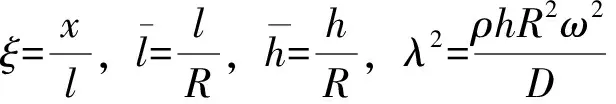
(2)

简写为：

(3)

对圆柱壳段的左端，ξ=0， 代入上式得：

c={Z(0)}={Z(ξ)}L；

(4)

对圆柱壳段的右端，ξ=1， 代入上式得：

(5)

因此，从圆柱壳段左端状态矢量到右端状态矢量的场传递矩阵为：

(6)

1.1.2 圆柱壳场传递矩阵的精细积分求解

传递矩阵的高精度对传递矩阵法结果的精度至关重要，若像指数函数的Taylor展开，采用硬展开的方式计算壳段的场传递矩阵eA，经验证场传递矩阵精度损失较大。精细积分是近年来出现的一种有效矩阵指数求解方法。

为得到高精度的场传递矩阵eA，采用精细积分法计算。取m=2N，将矩阵A缩小1/m倍后，保证Taylor级数展开计算的可靠性。

[I+T(0)]2N。

(7)

式中：I为单位矩阵。

精细积分法能获得高精度计算结果的根本原因是数值计算的相对误差不随递推过程的进行而扩散。具体体现为以下2点：

1)按Taylor展开计算T(0)，精度得到保证；

2)以上述的T(0)为基础，不断执行以下循环T(i+1)⟸2T(i)+T(i)T(i)，(i=0,1,2,…,N-2,N-1)。

能保证精度不损失，且编程计算方便。通过适当选取N(m=2N)，可使计算结果达到很高精度。

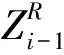
(8)

(9)

矩阵C为结构的总传递矩阵。因各个子传递矩阵中的元素与ω有关，C中各个元素一般亦依赖于ω。

(10)

可得频率方程：

DetC1=0。

(11)

对于两端固支的圆柱壳结构，有：

(12)

可得频率方程：

DetC2=0。

(13)

求出固有频率之后，带回线性方程组，然后从左端截面出发，分段利用场传递矩阵和点传递矩阵，得到中间各个截面的状态向量元素的相对比值，并获得模态向量。

1.2 圆锥壳自由振动传递矩阵

惯性力引起的分布荷载等与圆柱壳的情况类似，同样引进下列无量纲化变量：

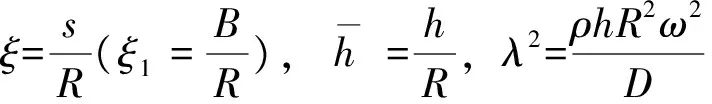
(14)

圆锥壳段的状态方程可写成矩阵形式：

(15)

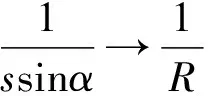
一般地，ξ代表的任意截面处状态向量可表示为：

{Z(ξ)}=TF(ξ){Z(ξ1)}， (ξ1≤ξ≤ξ2)。

(16)

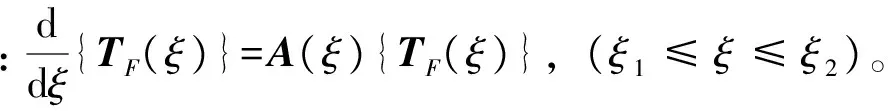
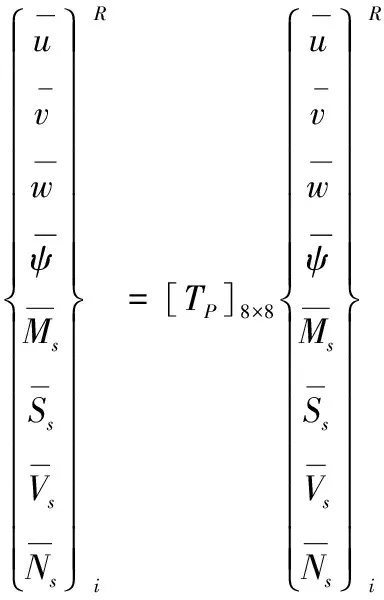
(17)

典型边界条件下的圆锥壳的自由振动的固有频率和模态的求解过程，与圆柱壳情况的求解过程类似。

1.3 锥-柱结合壳自由振动的传递矩阵

圆柱壳段和圆锥壳段的传递矩阵前面已详述，如图2所示，c代表圆锥壳，o代表圆柱壳，式(18)给出了圆锥和圆柱相结合处的位移和内力连续条件。

图2 圆锥-圆柱结合处的位移、内力连续条件Fig.2 Continuous condition of displacements and internal forces of the link

(18)

(19)

典型边界条件下的锥柱结合壳的自由振动的固有频率和模态的求解基于前文圆锥壳和圆柱壳的求解方法。

2 数值计算及讨论

为说明本方法的可靠性，分别进行圆柱壳、圆锥壳以及锥柱结合壳的固有振动特性算例计算并与有限元软件Ansys计算结果对比。算例参数如下：

圆柱壳参数：壳体材料的杨氏模量为2.1×1011Pa，壳体材料的泊松比为0.3，壳体材料的密度为7 850 kg/m3，圆柱舱段的长度为0.5 m，半径为1.0 m，壳体厚度为0.01 m；

圆锥壳参数：材料同圆柱壳，圆锥角为30°，圆锥壳左端的半径为0.422 67 m，圆锥壳右端的半径为1.0 m，壳体厚度为0.01 m；

锥柱结合壳算例由以上圆柱壳和圆锥壳组合而成。

圆柱壳两端简支和固支边界条件下固有频率与Ansys计算结果进行对比，如表1所示。锥柱结合壳简支边界下其固有频率与Ansys计算结果进行对比，如表2所示。对比结果表明了本求解方法的准确性。

同时从计算结果可以看出，锥柱耦合后会出现大量锥柱耦合模态，锥柱结合壳振型中也会出现以锥柱结合处为节点的柱壳或者锥壳自身振型，但这些振型对应的模态频率相应于单独圆柱壳或圆锥壳在简支或固支条件下模态频率有一定程度降低。

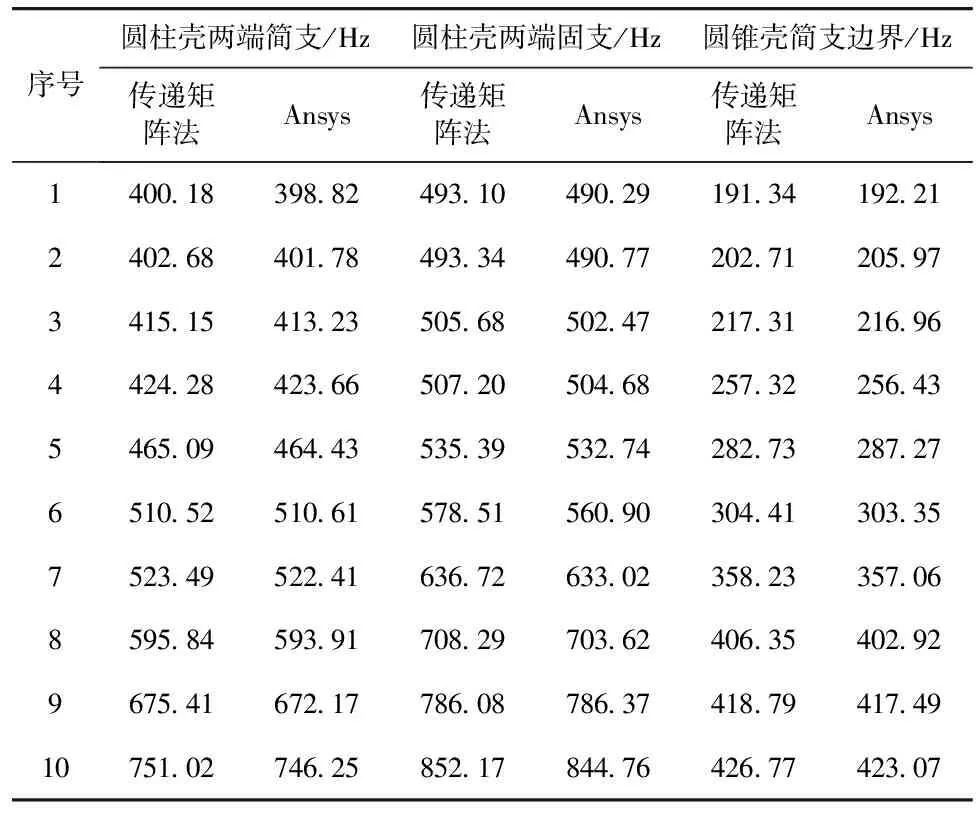
表1 不同边界下圆柱壳和圆锥壳的固有频率

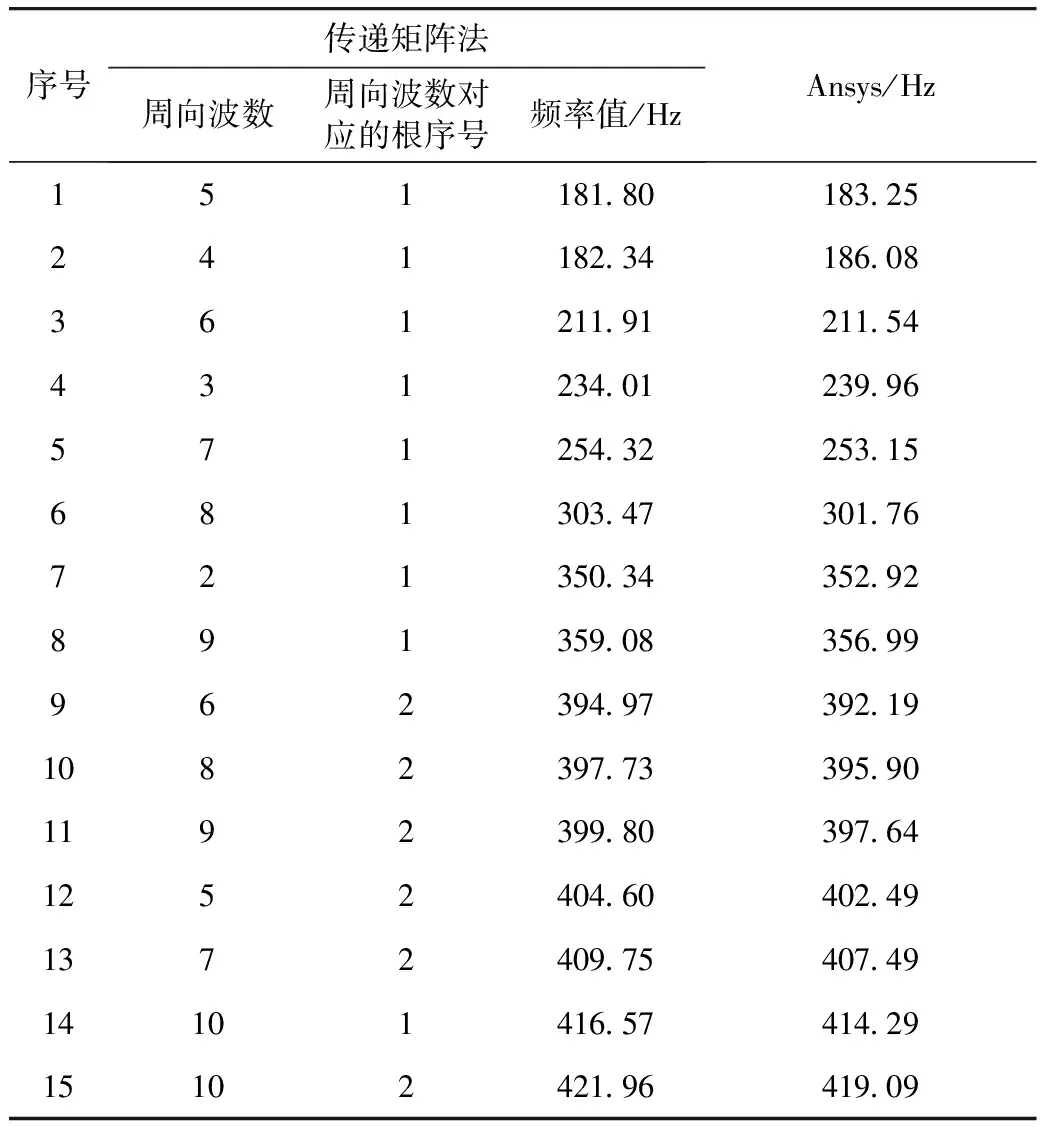
表2 锥柱结合壳简支边界下的固有频率

3 结 语

本文给出了基于壳模型的圆柱壳、圆锥壳以及锥柱结合壳的运动矩阵方程，采用精细积分以及Runge-Kutta-Gill法进行场传递矩阵计算，进一步分析了不同边界条件下的圆柱壳、圆锥壳以及锥柱结合壳的自由振动特性。算例数值计算结果表明：

1)本文提出的传递矩阵法可获得全面的、较高精度的固有频率和模态振型；给出的精细积分以及Runge-Kutta-Gill的数值计算方法的相对误差不随递推过程的进行而扩散，可获得高精度数值结果；

2)锥-柱壳耦合后锥、柱壳独立振型下的模态频率较单独圆柱壳或圆锥壳在简支或固支条件下的模态频率低。

本文方法对于变厚度壳体以及加筋壳体也不难获得解决。

[1] KALNINS A.Free vibration of rotationally symmetric shells[J].J.Acoust.Soc.Am,1964,36:1355-1365.

[2] ROSE J L,MORTIMER R W,BLUM A.Elastic-wave propagation in a joined cylindrical-conical-cylindrical shell[J].Exp.Mech,1973,13:150-156.

[3] HU W C L,RANEY J P.Experimental and analytical study of vibrations of joined shells[J].AIAA J,1967(5):976-980.

[4] EFRAIM E,EISENBERGER M.Exact vibration frequencies of segmented axisymmetric shells[J].Thin-Walled Struct,2006,44:281-289.

[5] PATEL B P,GANAPATHI M,KAMAT S.Free vibration characteristics of laminated composite joined conical-cylinderical sheIls[J].J.Sound Vib,2000,237:920-930.

[6] IRIE T,YAMADA G,KANEK Y.Free vibration of a conical shell with variable thickness[J].J.Sound Vib,1982,82:83-94.

[7] 黄玉盈，向宇.变厚度圆柱蓄水池动力分析的传递矩阵法[J].振动工程学报，1989,2(4):23-32.

HUANG Yu-ying,XIANG Yu.Free vibration of a circular cylindrical water storage pond with variable thickness based on transmits matrix method[J].Journal of Vibration Engineering,1989,2(4):23-32.

Application of transfer matrix method for analyzing natural vibrational characteristics of isotropic coupled cylindrical-conical shells

GUAN Shan-shan1，CAO Wei-wu1，XIE Guan-mo2

(1.Wuhan Second Ship Design and Research Institute,Wuhan 430064,China； 2.Wuhan University of Technology,Wuhan 430070,China)

The transfer matrix and the solution method for analyzing natural vibrational characteristics of isotropic cylindrical shells, conical shells and coupled cylindrical-conical shells are expressed in this paper. Precise integration and Runge-Kutta-Gill methods are used to solve the matrixes improves the precision and the efficiency of the solution.And the influence on vibrational characteristics of the coupling of the cylindrical shell and the conical shell is discussed. Compared with the FEM, the method described in the paper is efficient.

coupled cylindrical-conical shells；transfer matrix method；precise integration methods;natural vibrational characteristics

2013-05-23；

2013-12-02

关珊珊(1982-)，女，工程师，主要从事舰船减振降噪工作。

TB53；U661.44

A

1672-7649(2014)09-0032-05

10.3404/j.issn.1672-7649.2014.09.006