SKH51磨削粗糙度模型研究及工艺优化应用*
2014-07-24肖军民
肖军民,谢 晋
(1.中山职业技术学院,广东 中山 528404 ;2.华南理工大学 机械与汽车工程学院,广东 广州 510640 )
SKH51磨削粗糙度模型研究及工艺优化应用*
肖军民1,2,谢 晋2
(1.中山职业技术学院,广东 中山 528404 ;2.华南理工大学 机械与汽车工程学院,广东 广州 510640 )
基于SKH51高速钢磨削试验,利用最小二乘多元线性回归方法,推导并求解出了基于磨粒尺寸的表面粗糙度预测模型。基于求解出的粗糙度模型,利用序列二次规划优化方法针对企业实际的磨削问题,优选了合适型号的砂轮和磨削工艺参数。
磨粒尺寸;表面粗糙度;预测模型;磨削;优化;SKH51
Abstract: Based on experiments of grinding for SKH51 high-speed steel, the prediction model of surface roughness based on abrasive particle size is established by using of regression analysis method of least square. Aiming at the actual grinding problem in the enterprise, based on the model of surface roughness the appropriate model of grinding wheel and the optimal grinding parameters can be obtained by using of optimization method.
Key words: abrasive particle size; surface roughness; prediction model; grinding; optimization; SKH51
0 引 言
要实现磨削工艺参数的优化选择,建立相应工件材料的磨削质量模型是非常关键的。文献[1]就对外圆切入磨削的参数优选进行了研究,以最大磨削效率为目标函数,以表面粗糙度和工件的烧伤为约束条件,采用遗传算法对磨削工艺参数进行了优化选择。在国内已有研究者开展了磨削表面粗糙度模型的研究,但目前研究的重点都倾向于磨削工艺参数对加工表面质量的影响,而关于砂轮磨粒度对表面质量影响的研究则非常少[2-4]。工厂生产中根据实际情况可能需要采用不同磨粒度的砂轮对工件进行加工,而目前国内考虑砂轮磨粒度的磨削粗糙度模型非常少,为了能够更好地满足实际生产需要,在试验的基础上构建基于磨粒尺寸的粗糙度预测模型是非常有意义的。
1 试验条件和测试方法
1.1 试验条件
试验用的工件材料为进口高速钢,牌号为SKH51,SKH51相当于我国W6Mo5Cr4V2牌号的高速钢,SKH51高速钢的硬度为HRC62。试验选用如下加工设备:SGH-600型号的平面磨床,WA白刚玉系列磨粒的砂轮,砂轮尺寸规格为225×20×50.8。
1.2 测试方法
采用SJ-210P表面粗糙度测量仪(Mitu-toyo)测量工件表面,其测试方法:每次试验前,用单颗粒金刚石对砂轮进行修正,以减少砂轮引起的试验误差,每次试验均测量工件两端和中间共3个点的表面粗糙度,然后将这3个点的数值取平均值作为该次试验加工表面的粗糙度数值。
2 试验设计及数据分析
2.1 试验设计
实际加工中影响磨削表面粗糙度的因素非常繁多[5],但根据已有大量的研究成果表明,在无轴向进给的平面磨削中,影响表面粗糙度的工艺参数主要是砂轮线速度、工件线速度(工作台往复速度)和磨削深度。
文献[3]的研究则指出砂轮粒度对磨削粗糙度的影响非常显著,砂轮磨粒尺寸大小对表面粗糙度的影响远超过了所有磨削工艺参数。鉴于上述分析,因此确定砂轮磨粒平均尺寸,砂轮线速度,工件线速度和磨削深度四个因素为平面磨削粗糙度的主要影响因素。采用正交设计的试验方法,每个因素各取3个水平,正交因素水平如表1,具体试验方法利用标准正交表L27(313)进行磨削试验。依据文献[6]的磨削试验,可以获得表2所列的磨削粗糙度试验数据。
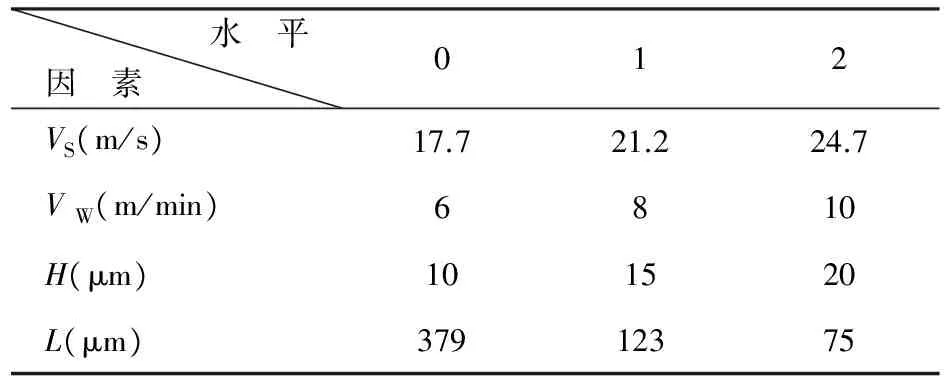
表1 试验因素和水平选取表
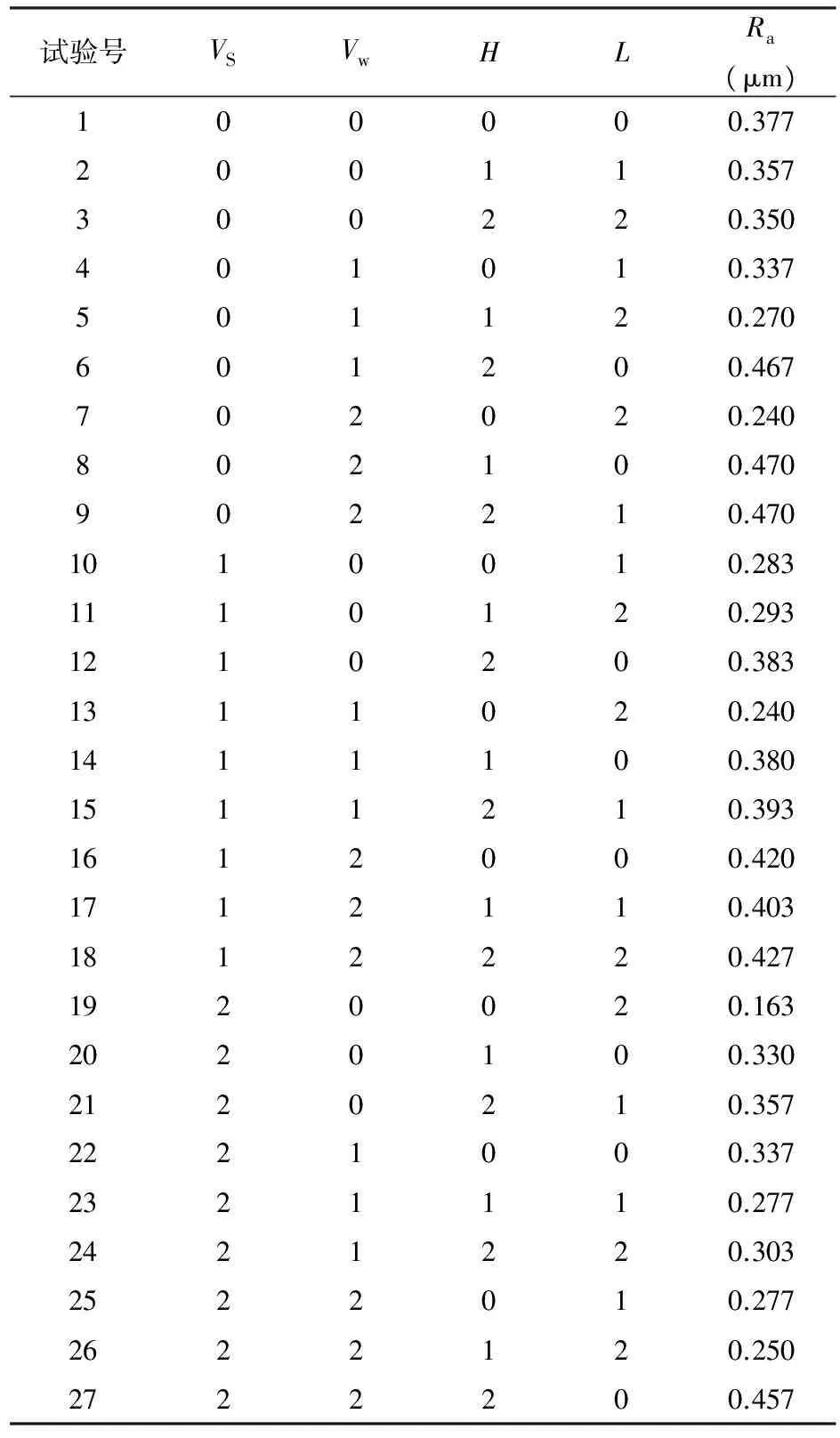
表2 磨削粗糙度正交试验数据
2.2 数据分析
为了更好地对试验结果进行预报和控制,需要对每个影响因素进行深入考察,因此需要对试验中涉及到的每个因素进行显著性检验[7]。假设β0=0,采用统计量算法,则有式(1):
(1)
式中:Cii为相关矩阵C= (X′X)-1中对角线上第i+1个元素,βi为回归模型系数的估计量,SE为剩余平方和,n为试验次数,m为变量个数。通过矩阵运算可以获得相关矩阵C。

根据式(1)可知:
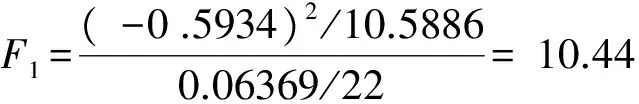
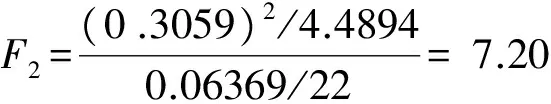
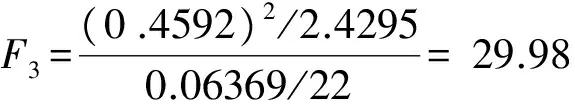
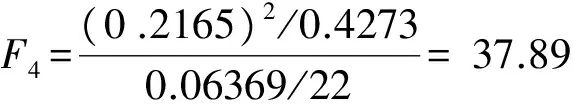
当检验水平为0.05时,查F分布表可得F0.05(1,22)= 4.30,由上述计算可知:F1>F0.05(1,22),F2>F0.05(1,22),F3>F0.05(1,22),F4>F0.05(1,22),且F4>F3>F1>F2。通过对各因素的F值分析可得出结论:砂轮磨粒尺寸、砂轮线速度、工件线速度和磨削深度四个因素对磨削粗糙度的影响都是非常显著的,而且砂轮磨粒尺寸对表面粗糙度的影响是最强的,其次分别是磨削深度、砂轮线速度和工件线速度。
3 表面粗糙度模型构建
传统磨削粗糙度经验公式广泛使用指数函数进行表达,而笔者是在考虑磨粒尺寸对磨削质量影响的基础上开展的相关磨削试验,因此可建立式(2)的预测模型,该模型包含了4个参数。
(2)
式中:K为磨削条件综合系数;VS为砂轮线速度,m/s;Vw为工件线速度,m/min;H为磨削深度,μm;L为砂轮磨粒平均尺寸,μm。式(2)为典型的非线性函数,须将其转化为线性函数,因此对其两边取对数,可以获得式(3)。
LogRa= log (K) +C1logVS+C2logVW+
C3logH+C4logL
(3)
令y= logRa,C0= log (K),x1=logVS,x2=logVW,x3=logH,x4= logL,则指数方程可转化为线性方程式(4)。
y=C0+C1x1+C2x2+C3x3+C4x4
(4)
利用表2中的正交试验数据,对线性方程(4)进行多元线性回归,则可求解到方程中相应的系数:C0=-0.9680,C1= -0.5934,C2=0.3059,C3=0.4592,C4=0.2165 ,因此SKH51高速钢磨削粗糙度的预测模型为式(5)。
(5)
为了判定预测模型拟合程度的好坏,需要对回归方程式(5)进行统计量F的显著性检验,F值检验法规定试验因素为m,次数为n,给定显著性水平为0.05。若F
(6)
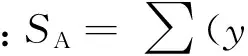
4 工程应用
4.1工程问题
某合资企业需要磨削某一批平面零件,零件的材料为SKH51高速钢,零件的表面粗糙度Ra要求不大于0.25μm。砂轮的外径尺寸为100mm,采用进口金刚石磨粒砂轮。由于现场条件限制,供现场使用的砂轮其磨粒度只有三种型号,它们的牌号分别是46# ,150#,280# ,砂轮的最高允许线速度均为35m/s。在考虑零件表面质量和砂轮磨损的条件下,生产企业需要选择合适的砂轮型号并提供较优化的磨削工艺参数。
4.2最小粗糙度的求解
选择的砂轮型号必须要满足产品的表面加工质量,因此首先要求解出三种型号的砂轮能达到的最好加工表面质量(即能达到的最小表面粗糙度数值),所以这个工程问题实际上就变成了对粗糙度函数求极值的问题了。为了求解出对应磨粒度型号的最小粗糙度数值,依据式(5)首先要求解出对应砂轮型号磨粒的平均尺寸。由于金刚石砂轮是进口的,经查阅相关国家的标准获得了相应砂轮型号的磨粒尺寸,46# ,150# ,280# 砂轮磨粒的平均尺寸分别是385μm,89.5μm,48.5μm。鉴于上述分析,可以建立如下对应三个粗糙度目标函数:
为了零件达到相应的表面质量,实际生产中还必须满足一些其它条件,结合SKH51高速钢磨削试验的实际情况和磨削经验,给出如下约束条件:
(1) 砂轮线速度:VS≤30;
(3) 磨削深度:10 ≤H≤20
对于多元非线性约束最小化问题的求解目前已有序列二次规划法、遗传算法、粒子群算法、人工神经网络、差分进化算法等许多优化方法[8]。由于序列二次规划法(SQP法)算法不仅可靠,而且编程简单,所以采用序列二次规划法来求解磨削粗糙度的最小值。序列二次规划法的实现分3步:①拉格朗日函数Hessian矩阵的更新;②二次规划问题求解;③目标搜索和目标函数的计算。基于MATLAB软件编写相关求解程序[9],并获得了表3所列的优化结果。

表3 粗糙度优化求解结果
4.3砂轮型号的选择
从表3的优化结果可以知道,磨粒度为46# 的砂轮能达到的最小表面粗糙度为0.32 μm,比工件要求的表面粗糙度0.25 μm要大,所以磨粒度为46# 的砂轮不能满足生产需求。而磨粒度为150# 和280#的两种砂轮能达到的最小表面粗糙度均比要求的表面粗糙度0.25 μm要小,所以这两种型号的砂轮均可满足产品加工要求。砂粒度为280#的砂轮其磨粒平均尺寸要比150#的要小,而磨粒颗粒尺寸越小的砂轮磨削加工中就越易磨损,根据磨削经验在保证产品表面加工质量的情况下,一般应选取磨粒尺寸较大的砂轮型号,因此该企业应优选150#型号的砂轮,其工艺参数应选取表3的优选参数。
5 结 论
(1) 通过选定参数及磨削试验建立了SKH51高速钢磨削粗糙度模型,通过回归方程的显著性检验,证明了预测模型的可信度非常高。通过对试验数据统计量F的分析,可知影响磨削粗糙度的因素依次是砂轮磨粒尺寸、磨削深度、砂轮线速度和工件线速度。
(2) 预测模型中砂轮线速度对应的指数为负数,所以磨削粗糙度数值是随着砂轮速度的增加而降低的;工件线速度、磨削深度和砂轮磨粒尺寸对应的指数均为正数,因此磨削粗糙度数值随着工件线速度、磨削深度和砂轮磨粒尺寸的增加而升高。
(3) 以表面粗糙度为目标函数,利用序列二次规划法针对企业实际的磨削问题,获得了SKH51高速钢工件磨削的优化工艺,具体工艺如下:选用150# 型号的砂轮,砂轮线速度取30 m/s, 工件线速度取11.25 m/min,磨削深度取10 μm。
[1] Venu G A, Venkatesuara R P. Selection of Optimum Condition for Maximum Material Removal Rate with Surface Finish and Damage as Constraints in SIC Grinding[J]. International Journal of Machine Tools and Manufacture,2003, 43 (13): 1327-1336.
[2] 冯灿波, 谢桂芝, 盛晓敏,等. 不锈钢超高速磨削试验研究[J]. 中国机械工程, 2013, 24(3): 322-326.
[3] 吴玉厚, 张继鹏, 李颂华,等. 氮化硅陶瓷套圈内圆磨削表面质量的实验[J]. 沈阳建筑大学学报(自然科学版),2010, 26 (1): 176-179.
[4] 张坤领, 韦建军. 基于MATLAB的数控磨削球面粗糙度分析及仿真[J]. 组合机床与自动化加工技术,2010(3): 16-21.
[5] 杜金萍, 高术振, 刘春玲. 基于正交试验法的平面磨削用量的优选[J]. 机械研究与应用, 2007,20(4):63-65.
[6] 池龙珠. 基于回归设计技术的平面磨削表面粗糙度研究[J]. 机床与液压, 2013,41(3): 34-37.
[7] 田欣利, 佘安英. 基于回归分析方法的铣削表面粗糙度预测模型的建立[J]. 制造技术与机床,2008(11): 101-104.
[8] 赵 静, 路银川, 孔金生. 基于量子遗传算法的多峰函数优化研究[J]. 制造业自动化,2013,35(5):94-96.
[9] 张德丰.MATLAB实用数值分析[M].北京: 清华大学出版社,2012.
Research of Grinding Roughness Model for SKH51 Steel and Application of Process Optimization
XIAO Jun-min1,2,XIE Jin2
(1.ZhongshanPolytechnic,ZhongshanGuangdong528404,China; 2.SchoolofMechanicalEngineering,SouthChinaUniversityofTechnology,GuangzhouGuangdong510640,China)
2014-05-28
广东省高等学校优秀青年教师培养计划资助项目(编号:Yq2013195)
肖军民(1978-),男,江西吉安人,副教授,硕士,主要从事先进制造技术等方面的科研工作。
TG581
A
1007-4414(2014)04-0118-03
