大斜度桥梁斜塔钢构爬模刚度仿真和结构优化*
2014-07-24李建平王祥军杨基好
李建平,阮 杰,王祥军,杨基好
(1.中南大学 机电工程学院,湖南 长沙 410083; 2.高性能复杂制造国家重点实验室,湖南 长沙 410083; 3.中南大学-中铁五新集团联合研究中心,湖南 长沙 410100; 4.中铁十局集团有限公司,安徽 淮北 235000)
大斜度桥梁斜塔钢构爬模刚度仿真和结构优化*
李建平1,2,阮 杰1,2,王祥军3,杨基好4
(1.中南大学 机电工程学院,湖南 长沙 410083; 2.高性能复杂制造国家重点实验室,湖南 长沙 410083; 3.中南大学-中铁五新集团联合研究中心,湖南 长沙 410100; 4.中铁十局集团有限公司,安徽 淮北 235000)
以淮北相王大桥为背景,对大斜度桥梁斜塔钢构爬模进行刚度仿真分析和结构优化。通过建立钢构爬模有限元模型,并导入Workbench14.5进行仿真分析,得出爬模危险应力集中区域及最大变形量位置。并对下侧立面爬模结构进行优化,优化后爬模整体应力分布均匀,最大应力减少约30%,保证了爬模的刚度,控制模板的变形量。为大斜度桥梁斜塔钢构爬模设计提供了参考。
刚度仿真;爬模;大斜度;结构优化
Abstract: Combined the construction project of Huaibei Xiangwang Bridge, the stiffness simulation and structural optimizing of steel climbing form used in the large slope bridge tower are done. Through establishing the mode of climbing form, importing the mode to the Workbench14.5 proceeding simulation analysis to get the dangerous stress concentration area and maximum deformation position of climbing form. Then the structure of downside surface climbing form is optimized. The stress of downside climbing form after optimization is uniform and maximum stress is reduced about 30%, which ensures the stiffness and control the deformation of the template. The reference is provided to the design of the climbing form used in the large slope bridge tower.
Key words: stiffness simulation; climbing form; large slope; structural optimizing
0 引 言
钢构爬模是近年来一种新型的桥梁施工模板,它综合了大模板和滑动模板的优点[1-3],采用模板与爬模架联体同爬技术,解决了超高索塔、桥墩和桥梁斜塔成形的难题,目前已广泛应用于桥梁工程[4-5]。但随着工程技术的发展,倾斜30°左右大斜度桥梁斜塔的需求越来越多,爬模在斜塔上侧立面受浇筑混凝土浮力,下侧立面受浇筑混凝土重力的影响,受力状况复杂,到目前为止刚度未有明确的计算方法[6-11]。侧压力计算忽略了混凝土对模板产生的浮力与重力,设计刚度不足,导致模板变形,桥梁横截面不均匀,倾斜角度偏差过大,外表面凸起或陷下,影响桥梁质量和使用寿命,危害甚大[12-14]。2008年4月1日深圳地铁3号线3106标段因为爬模刚度不足,在浇筑混凝土时,造成爬模坍塌3死2伤的事故。如何设计大斜度爬模,保证爬模刚度,控制模板变形量,一直是困扰斜塔设计与质量的问题。笔者以淮北相王大桥为背景,对大斜度钢构爬模进行了刚度仿真分析,并对爬模结构进行优化,保证爬模的强度、刚度,并与实测结果进行了对比研究。
1 有限元模型的建立
淮北市相王大桥为无背索斜拉桥,桥面最宽处达45 m,其主塔倾斜角度为30°,采用钢构爬模施工。一次浇筑高度为4 m,是目前国内倾斜角度最大的爬模施工案例。采用中铁五新集团标准重型爬模系统,对于大倾斜工况下,钢构爬模系统受力复杂,笔者用Solidworks建立了爬模系统的模型。爬模系统由前后立杆、上横梁、承重平台、承重架、螺旋撑杆和模板等组成。活动部件通过销轴链接,整个爬模通过螺旋撑杆调节角度。爬模三维模型如图1所示。将三维模型导入到Workbench14.5中进行下一步分析[15-17]。设置材料属性,本系统由两种材料组成,模板系统为维萨板加木工字梁,其弹性模量E=9.86 GPa,泊松比μ=0.31,密度ρ=700 kg/m3。其余结构为钢构件,其弹性模量E=211 GPa,泊松比μ=0.3,密度ρ=7 850 kg/m3。模型用SOLID187实体单元划分,有限元计算模型如图2。
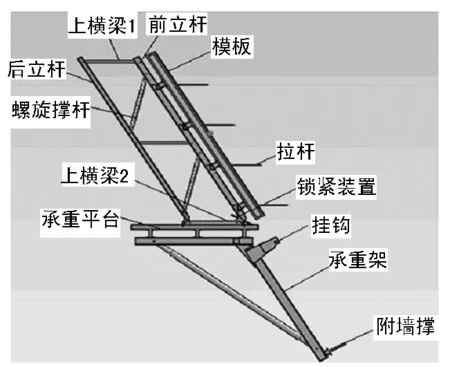
图1爬模三维模型
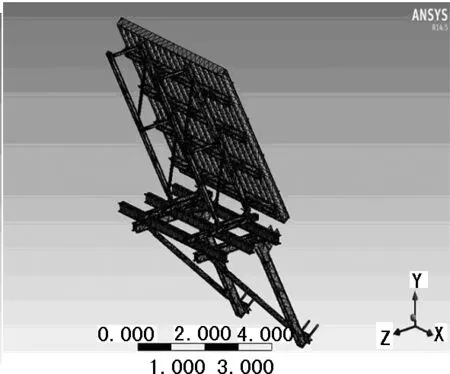
图2 有限元计算模型
2 刚度分析理论及边界条件
2.1 刚度分析理论
有限元的基本思想是将连续的求解区域离散为一组有限个,且按一定的方式相互连接在一起的单元组合体。物体被离散为更小的单元后,通过各单元进行分析,用单元的节点位移来表示单元中的应变、应力、结点力。然后将单元集合成离散化的结构模型进行整体分析,根据各节点处的平衡和协调条件微分方程求解出位移后,就可以利用位移算应力应变等。一般的有限元解法包括结构离散化成单元,单元分析,整体分析三个主要步骤。大斜度钢构爬模系统刚度仿真分析属工程结构静力学范畴,其结构可视为立体的弹性体。弹性体在外力作用下将发生位置的移动和形状的改变,其内部各点都将沿x、y、z坐标轴方向产生位移。各点沿x、y、z方向的位移以u、v、w表示,这些位移为各点坐标的函数,即:
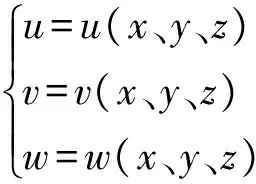
(1)
由弹性力学可知,只考虑微小位移和微小变形,略去他们的二次或更高次幂,则应变与位移矢量间的几何关系是:
[ε]=[εxεyεzγxyγyzγzx]T
(2)
三维弹性体的应变分量用矩阵表示为:
(3)
弹性体受力作用,内部任意一点的应力状态也是三维的,用列向量表示为 :
(4)
在线弹性范围内,应力与应变间的物理关系矩阵表达式为:{σ}=[D]{ε}
(5)
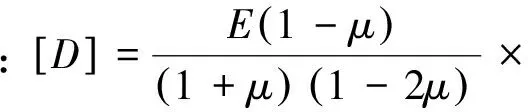
(6)
式中:[D]为弹性矩阵,完全取决于弹性常数E和μ。
2.2 边界条件
钢构爬模在施工时承重架挂钩挂在销轴上,边界条件为:
u1=0,v1=0,w1=0
(7)
附墙撑顶在已浇筑桥墩上,边界条件为:
w2=0
(8)
爬模主要承受自身重力和混凝土对模板产生的力。对于未初凝的混凝土近似于流体,混凝土对倾斜模板的合力垂直于模板面。取一边模板垂直另一边模板倾斜的模板体系进行分析,取h高度内混凝土,水平方向平衡方程为:
(9)
对h+dh高度内的混凝土,也有水平方向的平衡:
(10)
可得:
F(h)dh=P(h)sinαdl
(11)
故可推出:
F(h)=P(h)
(12)
上述推导中F(h)为垂直模板混凝土的侧压力或其反作用力,P(h)为混凝土对倾斜模板的产生的力或其反作用力,α为模板与水平面夹角,故可推导出倾斜模板的侧压力等于在相同深度处对垂直模板的侧压力,垂直模板的侧压力分布如图3所示。
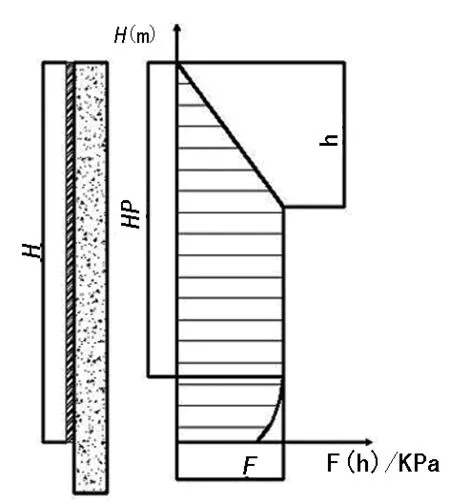
图3 模板侧压力分布曲线
其中:F可按以下两式计算,并取其较小值。
F=0.22γct0β1β2V1/2
(13)
F=γcH
(14)
式中:F为对模板的最大侧压力,kN/m2;γc为混凝土的重力密度,kN/m2;t0为新浇筑混凝土的初凝时间,h;t0可按实测确定,当缺乏试验资料时,可采用t0=200/(T+15)计算(T为混凝土的温度,);V为混凝土的浇筑速度,m/h;H为混凝土侧压力计算位置处至新浇筑混凝土顶面的总高度,m;β1为外加剂影响修正系数,不掺外加剂时取 1.0,掺具有缓凝作用的外加剂时取1.2;β2为混凝土坍落度影响修正系数,当坍落度小于30 mm时,取0.85,坍落度为50~90 mm时,取1.0,坍落度为110~150 mm时,取1.15。
考虑倾倒混凝土时冲击产生的作用于模板的荷载为2 kPa,高空作业时风垂直作用于模板的风载荷为1 kPa,同时本项目浇筑为泵送混凝土,荷载值需在标准值的基础上乘以安全分项系数1.2,计算得出作用于模板上的最大侧压力为64.2(kN/m2),故该爬模倾斜模板的边界条件为:
P(h)=
(15)
式中:P(h),kPa,l为倾斜模板长度,m ,α为模板与水平面夹角。
3 有限元仿真分析和结构优化
爬模在上下侧立面两种工况下,混凝土自下而上浇筑到顶部时受力最大,取这两工况进行仿真分析。上侧立面工况爬模前立杆与横梁成120°夹角;下侧立面工况爬模前立杆与横梁成60°夹角,两种工况如图4所示。
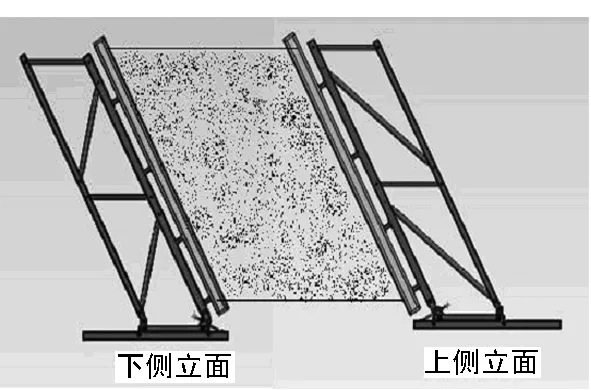
图4 爬模两工况示意图
利用Workbench14.5进行加载求解。在承重架销轴及附墙撑处施加固定约束,爬模自身重力由Workbench根据模型的体积自动求得,倾斜模板上施加侧压力边界条件,边界条件方程如式(15)。得到爬模系统在上下侧立面两种工况状态下总体应力和变形状况。挑选典型下侧立面工况展示Workbench分析图,如图5~6所示。
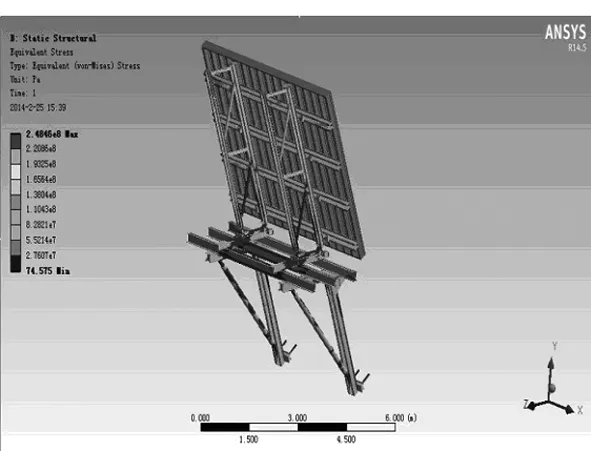
图5 爬模系统的总应力图
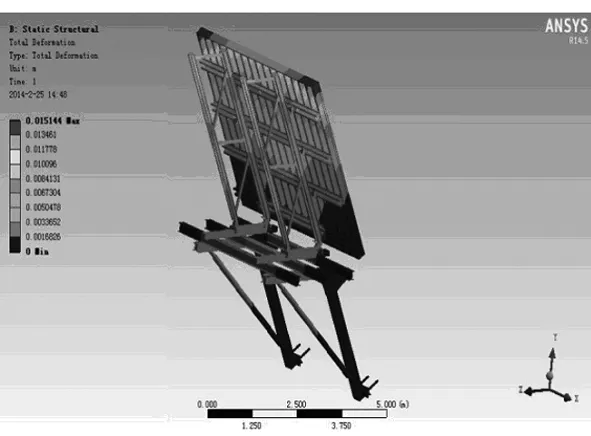
图6 爬模系统的总变形图
得到爬模在两种工况下最大应力、变形和位置,如表1所列。

表1 上下侧立面爬模最大应力和变形及位置
上侧立面爬模最大应力不超过220 MPa ,模板最大变形不超过10 mm,满足设计使用要求。而下侧立面爬模最大应力为248.5 MPa模板最大变形为15.1 mm,最大应力与最大变形大大超出许用要求。下侧立面比上侧立面工况的应力值要超出1倍,这是因为下侧立面受混凝土向下重力作用,而上侧立面受混凝土向上浮力的作用,故整体应力及变形较大,需对下侧立面爬模进行结构优化。从图中可看出爬模在承重架靠近承重平台处及下撑杆应力超过220 MPa,采用两副承重架承载力过小会导致架体坍塌,必须增加一个承重架;后立杆底端和螺旋撑杆应力及变形过大,导致模板倾斜较大,可在后立杆和承重平台之间增加撑杆以增加稳定性并减少应力集中。重新建模,并将优化后的模型导入Workbench进行仿真分析,总应力、总变形量如图7~8所示。
优化后爬模系统的最大变形为6.6 mm,在模板顶部两侧,最大应力为179.9 MPa ,在承重平台外侧处,符合设计要求,保证了爬模的强度、刚度和模板的变形量。
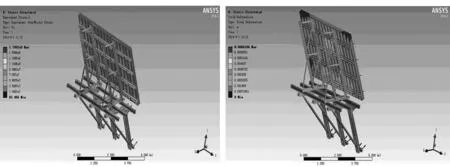
图7 优化爬模系统的总应力图 图8 优化爬模系统的总变形图
4 实验验证
优化后方案已成功应用在淮北相王大桥项目上,为了验证有限元理论计算模型是否正确,前期在施工现场对下侧立面模板进行了测试实验,采用电阻式应变片作为传感器, 先测出应变,然后根据公式得到应力和位移等。
在爬模模板上布置测点24个,共布置3列。左右两侧各布置一列,距离模板边缘200 mm,第3列布置在模板正中间,每列8个,均匀布置,为了减少误差测量6个浇筑节段内测点数据,再取各自测点平均值。从实验中得到下侧立面模板最大变形量在模板顶部两侧,平均值为6.4 mm ,与仿真值误差为3.1 %,同时模板变形量自下而上的变化趋势与仿真结果基本吻合,验证了仿真的可行性。
5 结 论
(1) 推导出大斜度桥梁斜塔钢构爬模模板混凝土侧压力边界条件,建立了刚度仿真分析有限元模型,为大斜度爬模仿真分析提供了依据。
(2) 通过有限元仿真分析了爬模强度和刚度,得到了爬模危险应力集中区域及最大变形量位置,下侧立面危险应力集中区域在后立杆底端,最大变形量在模板顶部。优化后最大变形量仿真值为6.6 mm,试验结果为6.4 mm,误差为3.1%,验证了仿真分析的可行性。
(3) 对于相王大桥30°倾斜爬模系统,下侧立面爬模的最大应力比上侧立面高出1倍,下侧立面爬模结构增加承重架与螺旋撑杆后,整体应力分布均匀,最大应力减少约30%。
[1] M. Ramesh Kannan, M. Helen Santhi. Constructability Assessment of Climbing Formwork Systems Using Building Information Modeling[J]. Procedia Engineering, 2013(64):1129-1138.
[2] 龙 琼,张 刚.液压爬模系统的构造及应用[J]. 重庆交通学院学报, 2006, 25(3):26-31.
[3] Xiaoyong Liu, Yiming Hu, Daoyang Chen, Lili Wang. Safety Control of Hydraulic Self-climbing Formwork in South Tower Construction of Taizhou Bridge[J]. Procedia Engineering, 2012(45): 248-252.
[4] Mar Alonso-Martinez ,Juan Josédel Coz Díaz ,Antonio Navarro-Manso ,Daniel Castro-Fresno. Bridge-Structure Interaction Analysis of a New Bidirectional and Continuous Launching Bridge Mechanism[J]. Engineering Structures, 2014(59):298-307.
[5] Zhongfu Xiang .The Construction Technology of Chongqing Chaotianmen Bridge[C]. Fuzhou: Bridge Design & Engineering, 2010.
[6] 成国强,刘松林.泵送·混凝土对模板侧压力分析[J].兰州铁道学院学报,1998, 17(2):21-26.
[7] Metin Arslan ,Osman Simsek ,Serkan Subasi. Effects of Formwork Surface Materials on Concrete Lateral Pressure[J]. Construction and Building Materials, 2004, 19(4):319-325.
[8] A. Santilli , I. Puente ,M. Tanco. A factorial Design Study to Determine the Significant Parameters of Fresh Concrete Lateral Pressure and Initial Rate of Pressure Decay[J]. Construction and Building Materials, 2010, 25(4):1946-1955.
[9] 王旭峰,刘继文.从地铁桥墩立柱模板坍塌事故分析探讨混凝土侧压力值[J].建筑技术,2009,40(8):734-737.
[10] Tian Ming-ge, Yi Wei-jian. Dynamic Behavior of Reinforced Concrete Frame Structure During Construction [J]. Journal of Central South,2008 ,15(3):418-422.
[11] Humbert A, Gross D, Muller R, Braun M, Van De Wal, R.S.W. Van Den Broeke .Deformation and Failure of the Ice Bridge on the Wilkins Ice Shelf, Antarctica [J]. Meteorology and Climatology Glaciology, 2010, 51(55):49-55.
[12] Uesugi M, Kishida H. Frictional Resistance at Yield Between Dry sand and Mild Steel[J]. Soils and Foundations, 1986, 26 ( 4) :139-149.
[13] 方武生. 大型桥梁变形测量方法及其在平寨特大桥施工监控中的应用研究[D]. 长沙:中南大学, 2007.
[14] Liu Yong-biao. Importance Assessment of Members-continuous multi-span Stone-Arch Bridge collapsing[J]. Energy Procedia, 2011(11):4500-4506.
[15] Moaveni, Saeed. Finite Element Analysis: Theory and Application with Ansys[M]. Prentice Hall,1999.
[16] 李 兵, 何正嘉, 陈雪峰. ANSYS Workbench设计、仿真与优化[M].北京: 清华大学出版社,2008.
[17] 王 鑫,麦云飞.有限元分析中单元类型的选择[J].机械研究与应用,2009(6):43-46.
Stiffness Simulation and Structural Optimizing of Steel Climbing form Used in the Large Slope Bridge Tower
LI Jian-ping1,2, RUAN Jie1,2, WANG Xiang-jun3, YANG Ji-hao4
(1.CollegeofMechanicalandElectricalEngineering,CentralSouthUniversity,ChangshaHunan410012,China; 2.StateKeyLaboratoryofHighPerformanceComplicatedManufacturing,ChangshaHunan410083,China; 3.JointResearchCenterofCentralSouthUniversity-ChinaRailwayWuxinGroup,ChangshaHunan410100,China; 4.ChinaRailwayTenthGroupCompanyLimited,HuaibeiAnhui235000 ,China)
2014-05-04
国家教育部留学回国人员基金资助项目(编号:76084)
李建平(1952-),男,湖南长沙人,教授,博士生导师,研究方向:材料成型工艺及机械装备研究。
TH69
A
1007-4414(2014)04-0096-04
