偏心组合桨搅拌槽内层流混合过程的数值模拟

梁瑛娜，高殿荣，拜亮

（1 燕山大学里仁学院，河北 秦皇岛 066004；2 燕山大学机械工程学院，河北 秦皇岛 066004）

在化工、冶金、生物、食品等行业扮演重要角色的搅拌设备，近年来受到越来越多的关注。机械式搅拌槽通过旋转的叶轮将能量传递给与其接触的介质，实现单相或多相介质的混合或反应。翁志学等[1]较早定性地获得了多层平桨和多层盘式透平桨的流型，发现层间距直接影响搅拌釜内涡环的数目，并通过流型解释了层间距对混合时间的影响。周国忠等[2-4]利用滑移网格法、RNG k-ε模型模拟了六直叶涡轮搅拌桨的三维流动场；利用k-ε模型模拟了搅拌槽内假塑性流体羧甲基纤维素钠（CMC）水溶液的三维流动场；在CFX软件基础上开发了用于混合过程计算的程序，并在流动场计算的基础上对单层涡轮桨搅拌槽内的混合过程进行了初步的数值研究。李志鹏[5]采用粒子成像测速（PIV）技术对单层、双层Rushton涡轮桨和多种曲面涡轮桨的流动特性进行了实验研究；在Fluent基础上编写大涡模拟程序，实现搅拌槽内单层Rushton涡轮单循环流型和双层Rushton涡轮多种复杂流型的大涡模拟，基于Realizable k-ε湍流模型对多种曲面涡轮桨的压力和速度分布进行数值模拟。杨锋苓[6]采用分离涡模型对偏心搅拌槽内流体的流动与混合过程进行了数值模拟，分析了宏观不稳定性频率的影响因素，并进行了PIV实验验证。Sakakura等[7]模拟了双螺旋纽带搅拌槽内颗粒的循环时间和混合时间，且用冷模实验进行验证，吻合较好。Javed等[8]采用滑移网格法模拟了六直叶涡轮搅拌桨的混合时间，对比实验数据，结果一致。

国内外学者采用理论分析、数值模拟和实验测量等方法对湍流搅拌设备进行了较为深入的研究。但实际的化工过程越来越复杂，当混合高黏流体或处理对剪切敏感介质时，如何使搅拌槽内处于低雷诺数的层流状态而又不降低搅拌效率？本文拟采用CFD方法对双层直斜叶交替组合桨在装有甘油与水混合物的搅拌槽中进行中心、偏心层流搅拌的流场特性、示踪剂扩散过程、示踪剂浓度响应曲线和混合时间进行数值模拟，研究结果希望为层流搅拌槽的设计和应用提供有价值的参考。

1 物理模型

1.1 搅拌槽及搅拌桨结构

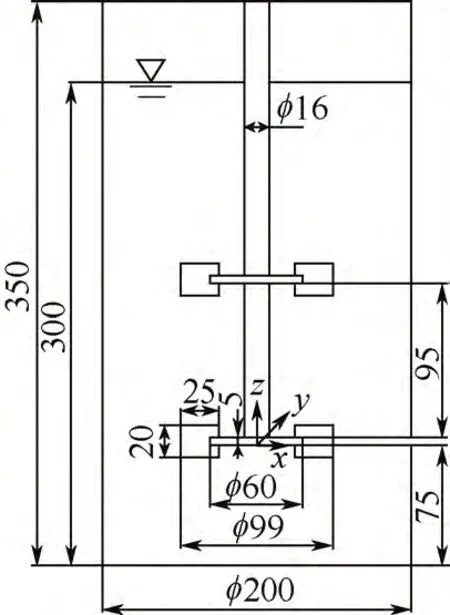
图1 双层桨搅拌槽结构（单位：mm）

图2 直斜叶交替组合桨

根据工业实际选用圆柱形平底搅拌槽，结构如图1 所示。对于高径比较大的搅拌槽，采用双层桨达到理想的搅拌效果；直叶片产生径向射流，斜叶片产生类轴向射流，现综合直、斜叶片的流动特性 设计双层组合桨进行更充分的全局搅拌。如图2 所示，每层叶轮均设6叶片，叶片规格为25mm× 20mm× 2mm，直、斜叶片交替布置，斜叶片倾斜45°；偏心桨上下层叶轮分别相对转轴偏心10mm。

将同心桨放置在搅拌槽中心，形成转轴中心搅拌结构；将同心桨相对槽体中心向左偏移15mm，形成转轴偏心搅拌结构；将偏心桨放置在搅拌槽中心，形成叶轮相对转轴偏心搅拌结构。3 种不同的搅拌结构如图3 所示。

1.2 介质物性及流动状态

用于数值计算的槽内介质设置为甘油（丙三醇）与水的混合物，混合比例约为15∶1，非牛顿流体，选取转速N=240r/min，通过式（1）计算雷诺数Re。搅拌槽内介质参数见表1，可见搅拌槽内流体处于低雷诺数的层流状态。

2 数学模型

流体流动要受物理守恒定律的支配，任何流动问题都必须满足连续性方程和动量方程。在模拟混合过程、计算混合时间时，采用示踪剂浓度法，所以需要启用组分质量守恒方程，见式（2）～式（6）。

图3 3 种不同搅拌结构

表1 搅拌槽内介质参数

连续性方程

动量方程

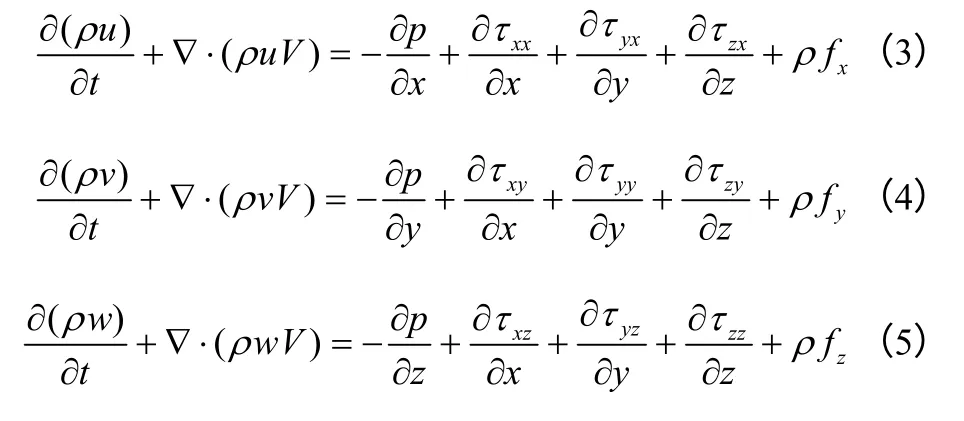
组分方程

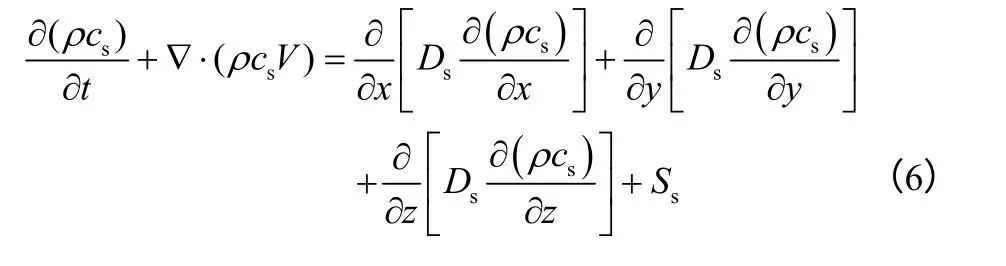
3 数值求解过程

3.1 网格划分

靠近搅拌桨的区域几何结构相对复杂，介质流动较为激烈，故采用不同尺寸非结构四面体网格相结合的方法，将搅拌槽内流体区域划分为桨叶区和普通区，对上、下层桨叶区网格进行局部加密。

3.2 边界条件设定

使用多重参考系法（MRF）进行流场模拟，将上、下层桨叶区设定为动区域，其内流体与搅拌桨进行同速转动；普通区设定为静区域，其内流体视为静止。动区域和静区域通过内部界面进行数值交换。搅拌轴、叶轮和桨叶壁面均设定为动壁面边界条件，处于动区域内的叶轮、桨叶和部分转轴壁面相对周围运动流体是静止的；处于静区域内的转轴壁面相对周围静止流体是运动的，转速为240r/min。搅拌槽内壁设定为静止壁面边界条件。自由液面设定为对称边界条件。

3.3 计算方法

采用Laminar 层流模型，压力速度耦合采用SIMPLE 算法，压力离散选择Standard 格式，动量离散选择First order upwind。将各变量的收敛残差设定为10-4，进行一定步数的迭代，待计算收敛后，便可得到搅拌槽内流场的稳态分布。

在此基础上求解示踪剂浓度场，启用组分传递模 型（ species model ）， 激 活 组 分 传 输 项（species-tracsport），但不激活反应项（reactions），这样组分之间就只是相互混合，而不会发生化学反应。在加料点A（70, 0, 280）处用Patch 功能打上示踪剂的补丁，同时设置示踪剂属性和主体介质相同，设定浓度收敛残差为10-7。锁定动量方程，时间步长设为2ms，单独求解浓度方程。加料点及监测点具体位置如图4 所示。

4 计算结果分析

4.1 铅垂面速度场

层间距的设置对搅拌槽内的流场有着重大影响。双层直叶桨产生径向流，当层间距（h）≥搅拌槽直径的一半（T/2）时，每层桨上下产生两个涡环，槽内呈现稳定的四涡环流态，即“平行流”。当层间距（h）≤搅拌槽直径的1/3（T/3）时，叶片端部射流倾斜，互相吸引，双层桨间的两涡环消失，槽内呈现两个大涡环，即“连接流”。双层斜叶桨产生类轴向流，当层间距增大至约2T/3 时，槽内才可产生“平行流”[9]。本文采用双层直-斜叶组合桨，层间距设置为95mm，槽内仍产生4 个涡环，但双层桨间两涡环受空间限制，相比“平行流”有连接的趋势，如图5 所示。

图4 加料点和监测点位置

图5 3 种不同结构搅拌槽内y=0 铅垂面速度矢量

4.2 中间面轴向速度曲线

为更加深入地分析物料在搅拌槽内的扩散过程，现取y=0、z=127.5mm、x=-100～100mm 线段上的轴向速度描点，如图6 所示。文中轴向速度与z 轴的正方向相同时为正，反之为负。

可见，中心搅拌在上下层桨中间面轴向速度几乎为0，说明上下层桨叶产生的涡环汇合时速度基本水平，桨叶旋转对槽内物料的影响仅限于各自的半层内，中间面起了阻隔作用，属“平行流”[10]。偏心搅拌中间面上的轴向速度曲线基本呈正弦分布，阻隔现象被打破。其中转轴偏心搅拌槽内轴向速度左侧随距x=0 距离的增大先正后负，右侧先负后正；而叶轮相对转轴偏心搅拌情况刚好相反。从数值上看，右侧较左侧的轴向速度要小，其中转轴偏心搅拌更为明显。对照图5，发现这都是结构不对称所致。整体上看，叶轮相对转轴偏心搅拌的轴向速度较大，说明叶片转动半径的变化比搅拌桨位置的变化对轴向速度的影响要大。

4.3 示踪剂浓度扩散图

图6 双层桨中间面z=127.5mm 轴向速度曲线

对于搅拌槽中的两相或多相介质，如果其中一 相的浓度在全局内均衡，即认定混合完成。在数值模拟时，通常以示踪剂（将某一相设置为极少量）的浓度达到最终稳定浓度的±5%，作为混合完成的标志。从开始到混合完成所用的时间称为混合时间。对混合过程和混合时间的模拟，通常的做法是在搅拌槽的一处或多处加料，随后监测一处或多处示踪剂浓度的变化情况。为研究方便，本文选择实际操作方便的液面处A 点作为加料点，并在搅拌槽全局选取5 个监测点，如图4 所示。

图7～图9 显示在3 种不同结构搅拌槽内加料点A 加料，铅垂面y=0 内示踪剂浓度随时间变化的分布图，也即示踪剂的轴向混合状况。槽内介质为高黏度非牛顿流体，所以选取5s 为一个时间间隔，同时加入t=2s 时间点，以更全面地展示混合初期示踪剂的扩散情况。

可以看出，示踪剂浓度扩散初期呈现类似速度场的旋涡，说明示踪剂跟随主介质一起流动，同时受到转轴旋转吸引的作用，高浓度区域集中分布在转轴附近。其中叶轮相对转轴偏心搅拌槽中示踪剂已扩散至下层桨处，转轴偏心搅拌接近下层桨，而转轴中心搅拌则只到达上下层桨中间面。在t=5s时，示踪剂进一步扩散，浓度开始减小。随后，示踪剂逐步向整个槽内扩散，叶轮相对转轴偏心搅拌的混合能力始终领先，转轴偏心搅拌次之，转轴中心搅拌最差。当t=10s 时，两种偏心搅拌结构示踪剂均扩散至槽体下半层，而中心搅拌结构示踪剂由于中间面的阻隔作用还被牢牢锁定在上半层；当t=15s时，转轴中心搅拌示踪剂在上半层扩散趋于均匀，中间面上下浓度相差越来越大，致使其才开始向下半层扩散；当t=20s 时，叶轮相对转轴偏心搅拌槽内示踪剂在全局范围内达到均衡，无继续扩散能力，混合完成。

4.4 示踪剂浓度响应曲线

在A 点加料，3 种不同搅拌结构中示踪剂在5个监测点处浓度相应曲线对比如图10 所示。

图10(a)展示了转轴中心搅拌槽中5个监测点的示踪剂浓度响应曲线，对照图7 来看，由于中间面的阻隔作用，示踪剂先是被限制在搅拌槽上半层扩散，直至均衡，再通过浓度差逐步向下半层慢慢扩散，最终整个槽内达到稳定浓度。位于液面处的监测点1 距离加料点最近，其响应曲线上升较快，在t=5s 时达到峰值1.8，随后趋于稳定。位于上层桨叶处的监测点2 响应曲线上升最快，且分别在t=1.5s和t=4s 时达到峰值3.5 和1.9，说明示踪剂最先跟随主介质运动到此区域，由于中间面的阻隔回流，示踪剂在此区域多次振荡才趋于稳定。位于中间面的监测点3、下层桨叶处的监测点4 和槽底部的监测点5 响应曲线没有峰值，平缓上升，直至稳定。转轴中心搅拌的混合时间长达35s。

图7 转轴中心搅拌槽内示踪剂浓度扩散过程

图8 转轴偏心搅拌槽内示踪剂浓度扩散过程

图10(b)显示，转轴偏心搅拌槽中5 个监测点的响应曲线曲率差距缩小，监测点1、监测点2 和监测点3 曲线分别在t=4.5s、t=3.5s 和t=2s 出现峰值1.8、2 和2.1，随后下降趋于稳定；监测点4 和监测点5 由于距离加料点A 较远，曲线平缓上升至稳态值，但其曲率同比图10(a)中的要大，这代表了更快的混合速度。转轴偏心搅拌的混合时间缩短至22s。

图10(c)中叶轮相对转轴偏心搅拌槽中5个监测点的响应曲线更为接近，监测点1、监测点2 和监测点3 曲线分别在t=4.5s、t=3.5s 和t=3.5s 出现峰值1.5、1.7 和1，之后很快下降至稳态值；监测点4和监测点5 则以更大的曲率上升至稳态值。叶轮相对转轴偏心搅拌的混合时间进一步缩短至18s。

5 条浓度响应曲线形态和峰值相差越大，代表搅拌过程中示踪剂扩散浓度越不均衡，可见：中心搅拌分区扩散用时长，效率低；而偏心搅拌打破了区域的限制，全局混合，用时短，效率高。

4.5 混合时间

现将3 种不同搅拌结构各监测点的混合时间列于表2。从表2 中可以清楚看到，各监测点混合时间的差值叶轮相对转轴偏心搅拌最小，转轴偏心搅拌较小，转轴中心搅拌最大。说明偏心搅拌轴向混合能力强，槽中各处几乎同时完成混合。从监测点的位置看，位于中间面的监测点3 的混合时间最短，这是因为其距离加料点A 较近，而且中间面的阻隔作用不会对其产生影响；距离加料点较近的监测点1 和监测点2 的浓度响应最快，但达到峰值后需要振荡一段时间才能趋于稳定，因此混合时间较长；位于下层桨处的监测点4 和槽底部的监测点5 距离加料点最远，浓度达到稳定需要的时间最长。

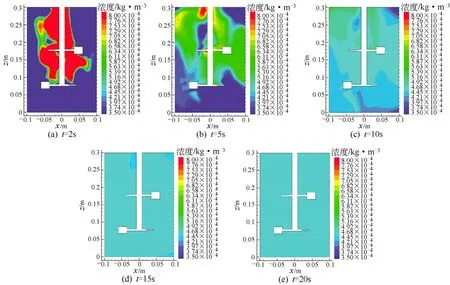
图9 叶轮相对转轴偏心搅拌槽内示踪剂浓度扩散过程

图10 不同监测点示踪剂浓度响应曲线

表2 不同搅拌结构各监测点混合时间

5 结 论

本文针对诸多工业场合介质对搅拌过程的低速要求，设计了双层直斜叶交替组合桨叶，对其中心及偏心搅拌过程进行了数值模拟，得出如下几个 结论。

（1）中心搅拌在上下层桨叶中间存在一个中 间面，介质只随搅拌桨在各自的半层内运动，轴向混合能力不足；偏心搅拌则打破了这种限制，介质在整个槽内作全局性运动，整体流动性好，轴向混合能力突出。

（2）转轴中心搅拌需要依靠搅拌槽上下层浓 度差的增大使物料继续向下半层扩散，混合时间长，混合效率低；偏心搅拌通过不对称结构使物料直接逐步扩散至下半层，混合时间缩短，混合效率高。其中叶轮相对转轴偏心搅拌的混合时间最短，说明叶片的不对称分布比转轴整体偏心具有更好的轴向混合能力，但合理的偏心距选择非常关键。

（3）监测点距离加料点较近，示踪剂浓度响应虽快但有峰值，需经振荡才能达到稳态值，调整时间较长；监测点距离加料点较远，示踪剂浓度响应较慢，调整时间也较长。只有位于中间面上的监测点具有较短的调整时间。

符 号 说 明

cs——组分s 的体积浓度

D——叶轮直径，mm

Ds——组分s 的扩散系数

fx，fy，fz——分别为单位质量体积力在x、y、z 方向的分量，m/s2

h——上下层叶轮间距，mm

N——转轴转速，r/min

p——压力，Pa

Re——雷诺数

Ss——组分s 的生产率

T——搅拌槽直径，mm

t——时间，s

u，v，w——分别为速度在x、y、z 方向的分量，m/s

μ——动力黏度，Pa·s

ρ——密度，kg/m3

τij——j 方向的黏性应力作用在垂直于i 轴的平面上的分量，Pa

[1] 翁志学，黄志明，李允明. 湍流搅拌釜多层桨层间距对搅拌特性的影响[J]. 化学工程，1983（6）：1-6.

[2] 周国忠，王英琛，施力田. 搅拌槽内三维流动场的RNG k-ε 数值模拟[J]. 北京化工大学学报，2002，29（2）：15-23.

[3] 周国忠，王英琛，施力田. 用CFD 研究搅拌槽内的混合过程[J]. 化工学报，2003，54（7）：886-890.

[4] 周国忠，施力田，王英琛. 搅拌反应器内计算流体力学模拟技术进展[J]. 化学工程，2004（3）：30-34.

[5] 李志鹏. 涡轮桨搅拌槽内流动特性的实验研究和数值模拟[D]. 北京：北京化工大学，2007.

[6] 杨锋苓. 偏心搅拌槽内宏观不稳定性的分离涡模拟及实验研究[D]. 济南：山东大学，2010.

[7] Sakakura Kei，Shiojima Takeo，Yamamoto Satoru. Numerical simulation of double helical ribbon agitators using three-dimensional DEM simulation[J]. Japan Society of Mechanical Engineers，2005，703（71）：722-766.

[8] Javed K H，Mahmud T，Zhu J M. Numerical simulation of turbulent batch mixing in a vessel agitated by a rushton turbine[J]. Chemical Engineering and Processing，2006，2（45）：99-112.

[9] 苗一，潘家祯，牛国瑞，等. 多层桨搅拌槽内的宏观混合特性[J]. 华东理工大学学报：自然科学版，2006，32（3）：357-360.

[10] Rutherford K，Lee K C，Mahmoudi S M S，et al. Hydrodynamic characteristics of dual rushton impeller stirred vessels[J]. AIChE J. 1996，42：332-346.