盾构重叠隧道施工力学行为分析

宋建禹

(铁道第三勘察设计院集团有限公司，天津 210017)

盾构重叠隧道施工力学行为分析

宋建禹

(铁道第三勘察设计院集团有限公司，天津 210017)

我国地铁建设的快速发展，就涉及地铁建设中上下重叠隧道的相关问题进行研究。利用三维有限元方法并结合广州某重叠盾构施工的地铁工程实例分析了下洞(左线)隧道受上洞(右线)开挖产生的影响范围、上洞盾构在不同推进力下对下洞位移、应力和应变产生的影响和下洞局部范围在有临时支护条件下随上洞开挖产生位移和内力变化。分析表明：下洞隧道结构受上洞盾构施工的影响表示形式为上洞盾构前方的下洞结构存在向下桡曲，而在后方则向上隆起，直至趋于一个定值，其中下洞盾构机的盾尾需在上洞盾构机盾头前方的50 m；上洞隧道在推进过程中，推进力是控制下洞结构变形的主要因素。此时，应严格控制上洞盾构隧道施工时盾构机推进力大小并仔细对下洞结构变形进行监测；对下洞隧道施作临时支撑可以有效减小位移和结构的受力特性；分析计算得出的结论对于盾构重叠隧道设计和施工有一定指导意义。

重叠隧道；盾构；力学行为分析；三维有限元

随着我国地铁的持续建设，地铁网络不断完善，城市地下空间开发利用的规模也不断扩大。进而使得在盾构开挖隧道时遇到重叠的现象愈加普遍。如何控制盾构重叠隧道中上洞或者下洞的开挖所引起临近洞室位移和内力变化，以确保重叠盾构隧道的顺利掘进和正常使用，对于我国城市地铁建设和地下空间开发利用具有重要意义。

在地铁重叠盾构施工中，上洞盾构施工会改变既有下洞管片结构的受力状态，从而对下洞产生不利影响。上洞的受力模式也不同于半无限体或无限体中修建单一洞室的一般状况。初始状态下的应力场一般也是经常多次的扰动，加上在施工过程中所引起的多次扰动，其受力往往是不对称的，表现出很大的变异性。简单的说，上洞的开挖会使地层中围岩的应力从原来的3次应力场演变到5次应力场。由于这种应力场的变化导致了上洞结构和下洞结构的受力变异，造成下洞结构的安全性和上洞施工的复杂性问题，这是不可回避和必须加以解决的问题，因此研究其复杂的受力机理和相应对策已成为当务之急。国内外也有很多学者对盾构重叠隧道的施工力学行为进行了研究[1-5]。

以广州某重叠地铁隧道工程为例，利用ANSYS11.0有限元软件[6]，对盾构重叠隧道进行了建模分析。研究了上洞盾构施工对下洞结构的影响，所得出的结论对于盾构重叠隧道的设计和施工有一定的指导意义。

1 上下重叠隧道盾构施工三维有限元模型

受旧地铁隧道区间的影响，左右线隧道(左线在上，右线在下)以上下重叠的形式修建，且采用盾构法施工，衬砌管片外径6.2 m，内径5.5 m，衬砌环宽度1.2 m，厚度0.35 m。衬砌环分别由1块封顶块+2块邻接块+3块标准块组成。均采用C50钢筋混凝土，抗渗等级P10(局部P12)制作。区间左右线为分开修建的两条单线隧道，全长1 028 m，上下隧道线间距为6～12 m之间。区间线路所经过的地段，覆土的表层为人工填筑的杂填土、素填土，其下为粉质黏土、残积砾质黏性土、砾砂，下伏基岩为全风化花岗岩、散体状强风化花岗岩；沿线地下水主要分为3类：第四系松散岩类孔隙水，赋存于第四系海积层及冲洪积地层中。风化残积岩孔隙裂隙水赋存于风化残积层中；基岩裂隙水 主要赋存于基岩中。地下水位埋深1.6～6.0 m，标高0.9～8.3 m。

使用ANSYS11.0有限元软件建立上下重叠隧道的三维有限元模型进行开挖分析，尺寸为长240 m，宽60 m，高60 m，上下重叠隧道盾构施工的有限元模型如图1所示。建模时，围岩采用solid45三维实体单元模拟，屈服强度采用Drucker-Prager原则；临时支撑(Ⅰ22b工字钢)、盾构管片、盾构外壳则采用ANSYS提供的混凝土单元shell63来模拟[7]，假设为弹性体，其中管片力学参数按《混凝土结构设计规范》(GB50010—2002)选取，考虑到管片衬砌结构是通过螺栓将单个管片连接在一起的整体结构，具有横观各向同性性质，采用均质体等效管片衬砌时，需乘以刚度折减系数0.8[8]。折减后的管片材料参数和地层参数见表1。

图1 重叠隧道盾构施工的有限元模型

表1 材料物理力学参数材料类型弹性模量E/GPa泊松比υ重度γ/(kN·m-3)粘聚力c/KPa内摩擦角φ/(°)1⁃2素填土0．0090．3919．919．528．83⁃1粉质黏土0．0340．3019．9281411⁃2残积砾质黏性土0．050．3518．5262117⁃1全风化花岗岩0．110．3318．6222317⁃2散体状强风化花岗岩0．2520．2519．52425盾壳(根据等刚度反算)2500．2570——管片24．60．2525——临时支撑28．50．2525——

隧道盾构施工是一个连续推进的过程，这一点在有限元里面是很难完全模拟，所以必须做一定的简化。假定盾构推进是非连续过程，规定盾构机每次向前推进是一步一步的，且每一步的距离为1.2 m(衬砌环宽度)，并通过改变单元材料(刚度迁移法)来反映盾构推进。根据ANSYS11.0所特有的命令流功能来实现，其数值模拟步骤可简单分为：①计算初始应力，②激活盾壳支护单元(改变材料为钢壳材料)并施加推进力(均布荷载)在刀盘上③把被杀死的管片单位材料改为混凝土材料。边界条件：地表为自由边界(为简化计算，地表面模拟为水平面)，未受任何约束；计算模型的左右边界分别受到x轴方向的位移约束，模型的地层下部边界受到y轴方向的位移约束，上部边界加上覆岩层实际的自重。

对于上下重叠隧道，存在先施工下部隧道再施工上部隧道与先施工上部隧道再施工下部隧道两种施工顺序。在分析过程中，考虑下部隧道先施工，再施工上部隧道。

2 数值模拟结果分析

2.1 下洞隧道受上洞盾构开挖产生的影响范围

为了分析下洞隧道受上洞盾构开挖产生的影响范围，假定当上洞盾构隧道的盾构刀盘在推进到150 m位置时，下洞隧道管片拱顶和拱底部位竖向位移的纵向分布情况。

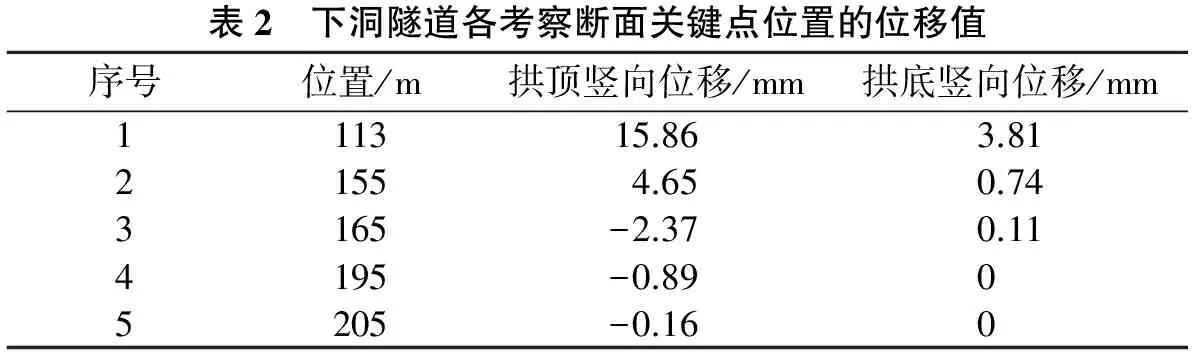
表2 下洞隧道各考察断面关键点位置的位移值序号位置/m拱顶竖向位移/mm拱底竖向位移/mm111315．863．8121554．650．743165-2．370．114195-0．8905205-0．160

图2 下洞隧道管片受开挖影响产生的位移

由表2和图2可以看出：上洞盾构施工引起的下洞拱顶与拱底竖向位移值变化规律具有较好的一致性。随上洞隧道在盾构机推进力为P=0.9 MPa推动到150 m位置时，下洞隧道管片在113～205 m之间(总长92 m)受到一定的影响，位移在113 m位置达到峰值，其中拱顶竖向位移为15.86 mm，拱底竖向位移为3.81 mm。从拱顶竖拱底竖向位移两者竖向位移的变化情况并结合以往盾构重叠隧道的施工经验，拟在113～165 m(总长52 m)范围内在下洞设置临时支撑，通过分析得出下洞盾构机的盾尾需在上洞盾构机盾头前方的50 m(155～205段)位置。

2.2 上洞盾构刀盘不同推进力对下洞管片产生的影响

由于盾构在推进过程中地质和周边环境的变化，盾构机参数的调整是一个实时的过程。为了进一步分析上洞盾构刀盘不同推进力对下洞管片位移和应力极值的影响，分析在相同条件下，计算推进力P=1.2～0.3 MPa，模数为0.3 MPa 4种工况下的模型。由上述模型计算得：考虑不同刀盘推进力作用效应后，4种工况下最大位移、纵向和横向最大拉压应力和应变大小如表3所示。

表3 不同推进力引起下洞隧道管片最大位移和应力推进力P/MPa最大竖向位移/mm最大水平位移/mm纵向最大应力/kPa拉应力压应力最大应变/10-5拉应变压应变横向最大应力/kPa拉应力压应力最大应变/10-5拉应变压应变0．33．261．82167．3286．121．87-1．2142．8522．461．01-0．810．68．622．17196．78102．313．10-2．0167．2328．341．78-1．640．916．324．08398．56154．215．89-4．6198．4741．233．01-2．151．222．176．12598．23298．167．12-5．42136．4886．234．12-5．16

由表3给出的最大竖向和水平位移值大小变化情况可以看出：当推进力从1.2 MPa减小到0.9 MPa时，最大竖直和水平位移都有不同程度的减小，具体为最大竖向位移从22.17 mm减小到16.32 mm，减小的幅度为26.38%，而最大水平位移从6.12 mm减小到4.08 mm，减小幅度约为33.3%;当推进力减小到0.6 MPa时竖向和水平位移分别减小为8.62 mm和2.17 mm，减小幅度为61%和64.5%；当推进力减小到0.3 MPa时，竖向位移和水平位移减小的幅度为85.3%和70.3%。从以上位移随盾构推进力减小的幅度可以看出推进力对下洞隧道管片位移变化有直接的影响，且随推进力的减小，竖向和水平位移均有明显的减小。

由表3给出的最大应力和应变值大小变化情况可以看出：当推进力从1.2 MPa减小到0.9 MPa时，下洞管片所受的应力和应变均明显减小，且推进力减小的幅度越大，最大应力和应变减小的幅度随之增大。其中纵向和横向拉应力减小幅度为33.4%和27.9%，压应力减小幅度为48.27%和52.2%，拉应变减小幅度为17.3%和26.9%，压应变减小幅度为15.8%和58.3%。下洞隧道管片最大应力和应变出现位置不随推进力的变化而发生变化，均出现在顶板附近，且受上洞盾构影响受力特征为：上缘受压，下缘受拉。并可发现下洞隧道管片所受主拉压应力和应变最大的区域也随推进力的减小而呈现减小的趋势。

由上位移、应力和应变分析可以得出：为防止下洞隧道管片开裂的一个主要措施就是要严格控制上洞盾构隧道施工时盾构机推进力参数。

2.3 临时支护条件下下洞随上洞开挖产生的位移和内力分析

图3 下洞隧道管片受上洞开挖影响产生的位移

通过以上对重叠隧道的数值模拟仿真分析，确定了下洞隧道受上洞盾构隧道开挖产生的影响范围和上洞盾构在不同推进力下对下洞管片产生的影响。针对以上分析，确定了下洞盾构隧道在上盾构机前后16 m和36 m范围内设置临时支撑。研究上洞隧道在盾构机推进力为P=0.9 MPa推动到150 m位置时，下盾构隧道管片竖向位移和内力变化情况。图3为下洞隧道管片受上洞开挖影响关键点位置产生的竖向位移变化图。

由图3可以看出，下洞隧道拱顶竖向位移变化较没有设置临时支撑时的平缓，且位移的最大值由无支撑时的15.86 mm减小到设置支撑后的11.68 mm，减小幅度为26.4%。分析位移减小的原因由于在下洞隧道设置了临时支撑，控制了下洞管片位移的变化，因此施工时在适当的位置设置临时支撑是很有必要的。其中拱底竖向位移变化规律跟拱顶的类似。

表4 下洞隧道各考察断面关键点位置横向内力统计表截面位置/m拱顶弯矩/kN·m轴力/kN边墙弯矩/kN·m轴力/kN拱底弯矩/kN·m轴力/kN最大剪力值/kN1057．612-420．687-64．029-639．45773．598-519．45881．95685102．359-517．569-93．569-817．956102．624-516．28489．652180134．846-570．694-122．687-1072．128134．923-564．24889．983150128．129-637．756-114．569-968．461128．543-534．235105．498

由表4给出的关键点位置横向内力变化可以看出，拱顶处弯矩最大值为134.846 kN·m，出现在上盾构机未通过的180 m位置。通过观察分析可以发现，边墙和拱底也有相似的变化规律。比较在180 m位置弯矩值的大小，可以看出拱底(134.923 kN·m)> 拱顶(134.846 kN·m)> 边墙(-122.687 kN·m)；拱顶处轴力最大值为-637.756 kN，出现在上盾构机正下方150 m位置。边墙和拱底处最大值则出现在上盾构机未通过的180 m位置，其值大小分别为-1 072.128 kN和-564.248 kN；横向最大剪力值的大小为105.498 kN，出现在上盾构机正下方位置。具体变化如图4所示。

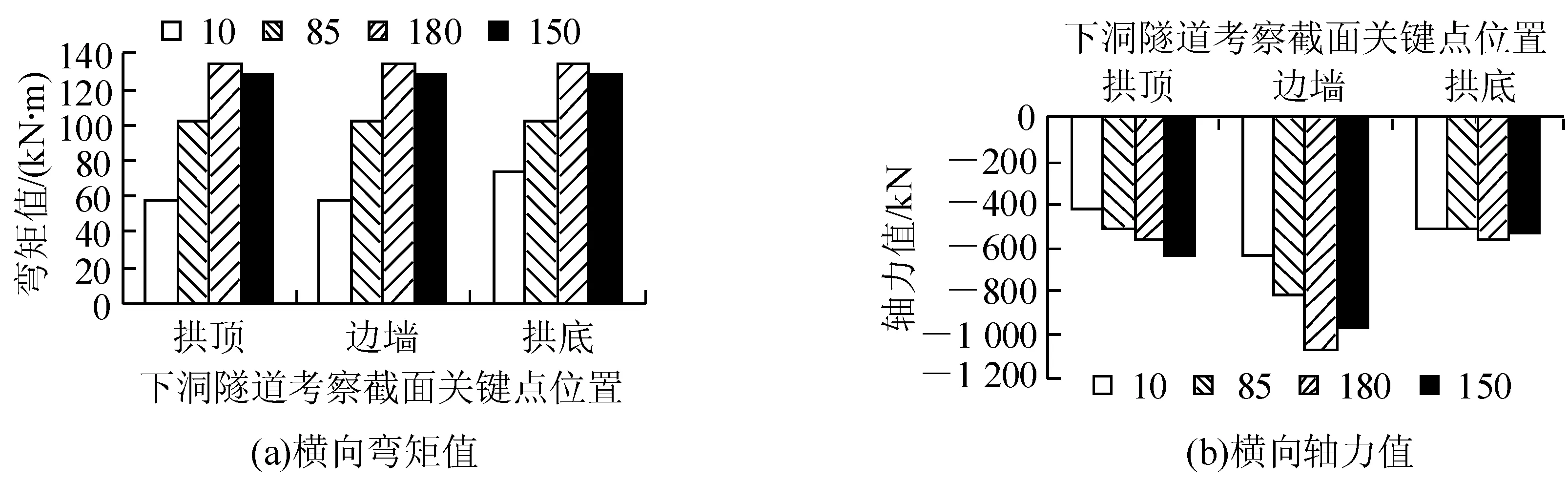
图4 下洞隧道各考察断面关键点位置横向弯矩和轴力图

由图4可以看出，随着上洞隧道盾构机推进到150 m的位置，下洞隧道所考察截面各关键点位置弯矩和轴力均有明显的增加，其中所考察截面各个关键点位置弯矩最大值均出现在180 m位置。拱顶轴力最大值出现在150 m位置，边墙和拱底则出现在180 m位置。通过以上的对比分析知，10 m和85 m断面内力在上盾构隧道修建完成后，由于卸载作用，下洞隧道管片结构上受力均减小。随着上盾构隧道的推进，在盾构机位置正下方的下洞隧道管片拱顶部位结构内力存在突变。

表5 下洞隧道纵向最大内力值和发生位置统计表关键点位置纵向最大弯矩/kN·m纵向最大轴力/kN发生位置/m拱顶-37．170-41．091135边墙24．672-142．291135拱底-18．428-223．250135

图5 下洞隧道135 m断面纵向弯矩和轴力图

由表5可以看出，纵向最大弯矩和轴力均发生在135 m处，且该断面的纵向最大轴力均为压力。由图5中的135 m断面纵向弯矩分布情况可以看出，最大负弯矩主要集中在拱顶部位，其值为-37.170 kN·m，最大正弯矩主要集中在左右拱肩部位，其值为34.383 kN·m，负弯矩比正弯矩在数值上大2.787 kN·m，差距不是很大。从纵向轴力分布情况可以看出，轴力最大值主要集中在拱底部位，其值为-223.250 kN。最小值主要集中在拱顶部位，其值为-41.091 kN，比最大轴力值小182.159 kN，相差较大。

3 结语

(1)根据“先下后上”的施工顺序，对上下重叠盾构隧道进行数值模拟分析。由分析结果表明：下洞隧道管片在113～205 m之间(总长92 m)受到上洞盾构的影响较明显，其中竖向位移在113 m位置达到峰值对此应采取相应的施工措施。为消除上、下洞盾构机相互影响的叠加，下洞盾构机的盾尾需在上洞盾构机盾头前方的50 m位置。

(2)通过对上洞不同推进力作用下引起下洞位移、应力和应变的归纳分析，认为对于重叠盾构隧道这种“卸荷”型地下建筑物的施工，在其上方修筑盾构隧道时不宜采用“加大推进力-快速通过”的盾构施工模式；盾构机在上洞隧道推进过程中，应严格控制施工参数和放慢掘进速度，这样对于减少对周围土体的拖带和对下洞盾构管片的影响都是首要的对策。并应全面对下洞隧道进行监测，特别是顶板部位。

(3)为有效降低上洞盾构施工对下洞的影响，拟对上盾构机工作面前后16 m和36 m范围内对下洞设置临时支撑系统。通过对设置临时支撑后下洞产生的竖向位移、横向和纵向内力的结果，认为在上洞盾构机以推进力P=0.9 MPa推进到150 m位置时引起下洞竖向位移最大值较无支撑时的减小，减小幅度为26.4%，且位移变化也变平缓。对于所考察断面关键位置横向内力拱底弯矩最大，轴力最小，而最大剪力刚好出现在上盾构机正下方所考察断面。通过对比分析可知，上盾构机已通过的，由于卸载作用，下盾构隧道管片受力均有减小。结构纵向受力最不利断面，出现在135 m处，该断面纵向弯矩最大，纵向轴力均为压力，通过对纵向抗弯能力进行检算，结构偏安全。

[1]孙均，刘洪洲.交叠隧道盾构法施工土体变形的三维数值模拟[J].同济大学学报，2002,30(4)：379-386

[2]仇文革.地下工程近接施工力学原理与对策的研究[D].成都：西南交通大学土木工程学院，2003.

[3]吴波，高波.地铁区间隧道施工对近领管线影响的三维数值模拟[J].岩石力学与工程学报，2002,21(增 2)：2451-2456.

[4]张志强，何川.双线盾构隧道与联络通道复杂结构受力分析[J].铁道学报，2002,24(6)：89-92.

[5]郑余朝．深圳地铁重叠隧道三维数值模拟分析[D]．成都：西南交通大学土木工程学院，2000.

[6]刘涛．精通ANSYS．北京：清华大学出版社，2002.

[7]佘健,何川.高速公路隧道施工全过程三维弹塑性数值模拟[J].西南交通大学学报,2005,40(3): 298-302.

[8]中华人民共和国住房和城乡建设部．GB 50010—2010 混凝土结构设计规范[S]．北京：中国建筑工业出版社，2010．

(责任编辑 刘宪福)

Analysis of Construction Mechanical Behavior forOverlapping Tunnel Shield

Song Jianyu

(Third Railway Survey and Design Institute Group Co. Ltd, Tianjin 210017, China)

In view of the rapid development of subway construction, issues related with the construction of vertically stacked subway tunnels are studied. Based on the example of Guangzhou metro overlap shield tunneling construction, through the dimensional finite element method, the influence of the upper hole (right lane) on the lower hole(left lane) construction, including the impact range of upper hole excavation on the lower hole, the influence of the upper hole shield under different propulsion on the displacement, stress and strain of the lower hole, and local displacement and force changes of the lower hole with temporary support conditions under the impact of the upper hole excavation. Analyses show the lower hole structure goes downward at the front end of the upper hole shield, and goes upward at the rear end, until it tends to be a constant value. In the case of the example of this article, the lower hole shield machine tail need to be 50 m in front of the upper hole shield machine head; In the advancing the process of the upper hole, propulsion force is the main factor to control lower hole structure deformation. thus the upper hole TBM propulsion should be strictly controlled during tunneling and lower hole structure deformation carefully monitored; temporary support structure for the lower hole tunnel can effectively reduce the displacement and stress. The conclusion of this article may provide some guidance for overlap shield tunnel design and construction.

overlapping tunnels; mechanical behavior analysis; dimensional finite element

10.13319/j.cnki.sjztddxxbzrb.2014.03.05

2013-06-25

宋建禹 男 1986年出生 硕士研究生

U452.2+5

A

2095-0373(2014)03-0023-06