Determination of Transport Properties of Dilute Binary Mixtures Containing Carbon Dioxide through Isotropic Pair Potential Energies
2014-07-24DelaraMohammadAghaieMohammadMehdiPapariandAmjadRezaEbrahimi
Delara Mohammad-Aghaie, Mohammad Mehdi Papari and Amjad Reza Ebrahimi
Department of Chemistry, Shiraz University of Technology, Shiraz 71555-313, Iran
Determination of Transport Properties of Dilute Binary Mixtures Containing Carbon Dioxide through Isotropic Pair Potential Energies
Delara Mohammad-Aghaie*, Mohammad Mehdi Papari and Amjad Reza Ebrahimi
Department of Chemistry, Shiraz University of Technology, Shiraz 71555-313, Iran
The present work is concerned with extracting information about intermolecular potential energies of binary mixtures of CO2with C2H6, C3H8, n-C4H10and iso-C4H10, by the usage of the inversion method, and then predicting the dilute gas transport properties of the mixtures. Using the inverted pair potential energies, the Chapman-Enskog version of the kinetic theory was applied to calculate transport properties, except thermal conductivity of mixtures. The calculation of thermal conductivity through the methods of Schreiber et al. and Uribe et al. was discussed. Calculations were performed over a wide temperature range and equimolar composition. Rather accurate correlations for the viscosity coefficients of the mixtures in the temperature range were reproduced from the present unlike intermolecular potential energies. Our estimated accuracies for the viscosity are within ±2%. Acceptable agreement between the predicted values of the viscosity and thermal conductivity with the literature values demonstrates the predictive power of the inversion scheme. In the case of thermal conductivity our results are in favor of the preference of Uribe et al.’s method over Schreiber et al.’s scheme.
intermolecular potential, transport properties, carbon dioxide, inversion scheme
1 INTRODUCTION
Carbon dioxide (CO2) is the principal product of carbon oxide, formed from the combustion of hydrocarbon fuels. It is the focus of public concern in recent years due to the increasing concentration of this gas in the atmosphere. The gas is implicated in the greenhouse effect. Therefore, the knowledge of thermodynamic and transport properties of carbon dioxide and its mixtures is necessary because of its importance in our environment and its increasing importance in chemical processes under supercritical conditions [1].
Since carbon dioxide is widely used in enhanced oil recovery processes, reliable modeling of the properties of mixtures composed of carbon dioxide and hydrocarbons is required for an accurate simulation and modeling of the carbon dioxide displacement processes [2]. In spite of the importance that carbon dioxide-hydrocarbon mixtures have for the oil industry, only a few measurements for their transport properties have been reported. Many important phenomena that occur in gas mixtures depend on molecular transport processes including viscosity, diffusion, and thermal conductivity. Transport properties are often critically important in engineering applications and for understanding phenomena such as combustion processes, hypersonic flows, and chemical vapor deposition. It is not possible to measure all the requisite transport properties, so we must have models to calculate them. This requires adequate information about the intermolecular potential and the underlying dynamics. Kinetic theory allows the prediction of transport properties of a mixture, if the potential energy of molecular interactions in the mixture is known as a function of intermolecular separation and orientation. A description of the potential as a function of intermolecular separation r, averaged over molecular orientations, suffices to calculate viscosity and diffusion coefficients [3].
Intermolecular pair potential can be obtained from both experimental observations and theoretical calculations (such as ab initio techniques). The fitting and inversion methods are the two different procedures used to extract the intermolecular potential energy functions from experimental data. In the traditional fitting procedure, a model potential is adopted with a certain number of adjustable parameters, which are varied until a good fitting is obtained to a given set of experimental data. The potentials obtained from this method do not appear to be unique since they depend upon the range of temperature and the property chosen for the test [4]. On the other hand, the main advantage of the inversion method is that it does not depend on the explicit assumption about the functional form of the potential and thus establishes a unique potential [5]. This iterative procedure produces the effective pair potential energy from data on bulk property measurements such as the viscosity, diffusion and second virial coefficient.
In continuation of our previous work on the calculation of potential energy functions and transport properties of different mixtures [6-12], the primary goal of the present work is to determine the potential energy functions for the binary mixtures of CO2with C2H6, C3H8, n-C4H10and iso-C4H10via the inversion of the reduced viscosity collision integrals at zero pressure and present the determined collision integrals, which are prerequisite for the calculation of the transport properties. Viscosity, diffusivity, thermal diffusion factor and thermal conductivity of the studied mixtures, encompassing a wide range of temperatures, are reported. These properties provide a valuable test for the reliability of the obtained potential energy functions.
2 THEORY
2.1 Transport properties of gases
Transport properties describe the process of relaxation to equilibrium from a state perturbed by application of temperature, pressure, density, velocity or composition gradients. The transport of mass, momentum and energy through a fluid is the consequence of molecular motions and interactions. Theoretical expressions for different equilibrium and non-equilibrium (transport) properties in terms of pair interaction energies are provided from the results of kinetic and statisticalmechanical theories [13]. The transport-coefficient expressions subsequently obtained by Chapman [14] and Enskog [15] through solving the Boltzmann equation, reduced the problem of transport in dilute simple gases to evaluation of explicit collision integrals [16] shown by Ω(l,s), which are well-defined for potentials of sufficiently short range, such as the Lennard-Jones potential [17]. Thus the Chapman-Enskog solutions of the Boltzmann equation provide a basis for computation of important transport coefficients, for both simple gases and gas mixtures [18]. The use of Sonine polynomial expansions for the Chapman-Enskog solutions first suggested by Burnett [19] has become the general method for obtaining the transport coefficients due to the relatively rapid convergence of this series [20, 21].
The transport properties appear finally in the Chapman-Enskog theory as a solution of infinite sets of simultaneous algebraic equations and can be expressed formally as ratios of infinite determinants whose elements are coefficients of the algebraic equations. The coefficients of equations are complicated functions, which depend on the species, the composition of mixture, and the collision integrals, Ω(l,s)[16]. The superscripts l and s appearing in Ω denote weighting factors that account for the mechanism of transport by molecular collision. For example, for the two transport properties, viscosity and diffusivity, the superscripts assume values of l=2, s=2 and l=1, s=1, respectively.
Collision integrals, Ω(l,s), for a fixed relative orientation in the Chapman-Enskog theory, result from a three-fold integration: on the inter-particle distance r, on the impact parameter b, and on the relative kinetic energy of colliding molecules, E [13].
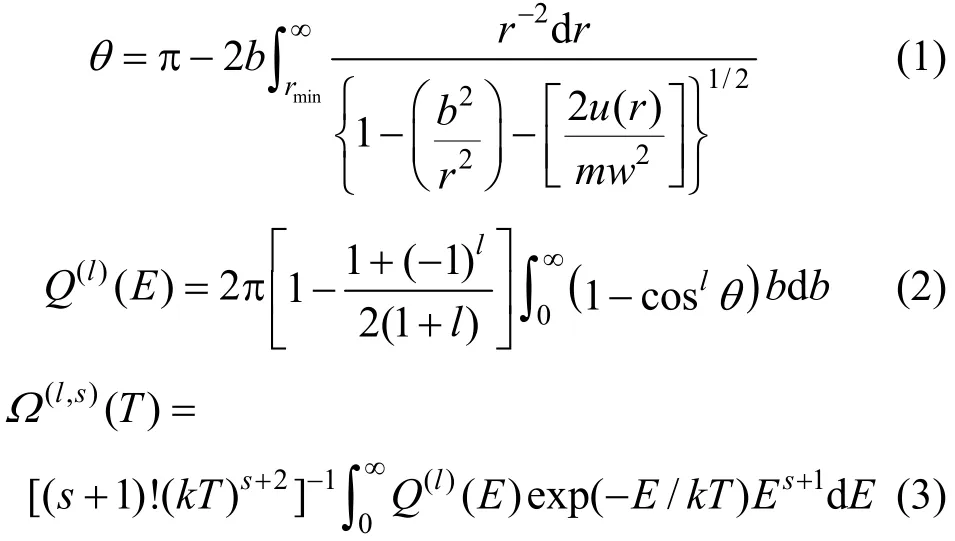
where θ is the classical deflection angle for u(r) interaction potential, rminis the distance of closest approach in a collision, w is the relative velocity of colliding partners, and Q(l)(E) represents the collision cross section, corresponding to l the moment. l and s is the collision integral order. k is the Boltzmann constant.
Numerical solution of these three successive integrals is required to obtain the collision integrals, which are necessary to calculate the transport properties. Using the potential u(r) as an input for Eq. (1), yields the scattering angle, θ, which in turn enters Eq. (2) and gives the transport cross section. This quantity would serve as the input information required in the calculation of collision integrals via Eq. (3).
The definition of collision integrals as dimensionless reduced quantities makes calculations of transport properties more convenient. The reduced collision integral is defined as

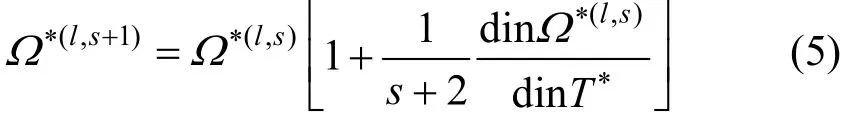
The reduced temperature T∗is usually defined as:

where the energy parameter, ε, is the well depth of the potential.
Certain ratios of the collision integrals appear in the mixture transport property formulas and higher order correction factors for the transport coefficients. These ratios, being slowly varying functions of T∗, are also useful in interpolation [22].
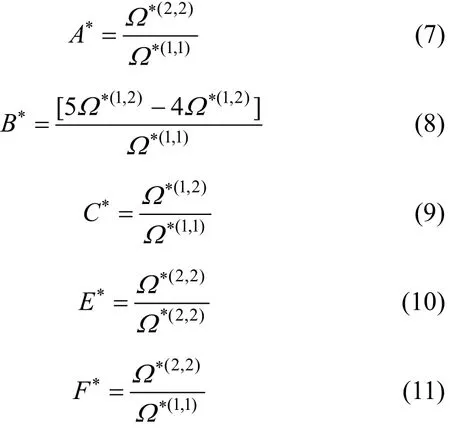
The magnitude of each of these ratios is approximately unity, and exactly unity for rigid spheres. Collision integrals and their ratios are functions of temperature and parameters of the selected model for intermolecular forces.
The viscosity and diffusion coefficients are concerned with transporting momentum and mass, respectively, and do not involve in internal degrees of freedom, so these transport properties can be described fairly well on the basis of a spherically symmetric potential. Inversion scheme produces an isotropic pair potential energy and so in our calculations of transport properties, the Chapman-Enskog theory retains its useful form but collision integrals must be averaged over all possible relative orientations occurring in collisions [23].
2.2 Theoretical basis of inversion procedure
The intermolecular forces determine all the thermodynamic properties of fluids, their kinetic coefficients, and most of the properties of crystals. Because usually characteristics that are some derivative of the intermolecular potential and not the intermolecular forces themselves are determined in direct experiments, there is a so-called inversion problem, which is a reestablishment of both the shape of potential and its parameters by using experimental data of different kinds [24].
The direct inversion procedure of Smith and co-workers [25, 26] provides a method by which a thermophysical datum point can be related to a point on the intermolecular potential energy curve. Of particular interest is the development of an inversion technique for bulk properties, which are readily available for a wide variety of substances. Among transport properties, the viscosity is the most important source for the extraction of information about the intermolecular potential energy. This is due to the easiness and accuracy in measuring of this property as compared to the other transport coefficients.
The inversion method for the viscosity is based on the idea that at a given T∗, the value of viscosity collision integral, Ω∗(2,2), is essentially determined by the values of u(r) over only a small range of separation distance, r [5]. As the details of this method has been given elsewhere [27], only a brief description will be provided here.
The necessary requirement to perform the inversion procedure is the determination of Gη, the inversion function, from an initial intermolecular potential energy. For real potentials it is found that Gηvaries with temperature in a complicated way, since the collisions have different energies and probe different parts of the potential function.
The following equations can be applied for the inverse power potential functions, where Gηis a numerical constant [28].
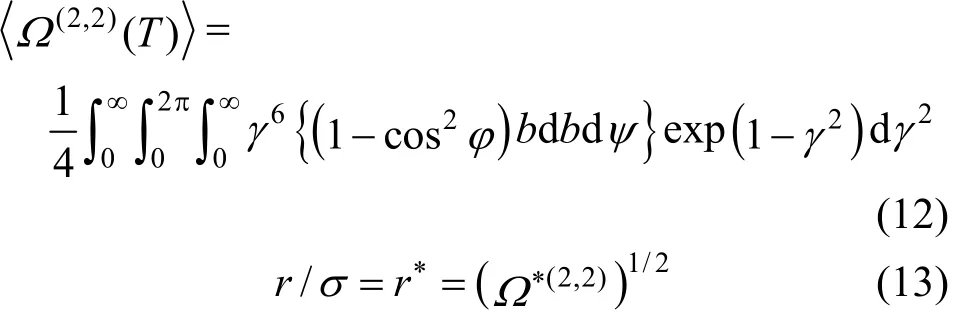
Following Viehland et al. [29], in this work, η is the viscosity, and Gηis estimated from the Lennard-Jones (12-6) model potential, which is a reasonable choice for the initial approximation of the intermolecular potential function. The inversion procedure begins by employing the experimental viscosity collision integrals from the corresponding states correlation equations, to convert data pointsto their relatedvalues on the potential energy curve through Eqs. (13) and (14). In order to develop an iterative scheme, it is necessary to extrapolate potential u(r) to both larger and smaller intermolecular separations. It is remarkable to mention that the inversion procedure is insensitive to the nature of extrapolation function. At long range, this extrapolation may be performed by means of an inverse sixth-power function:

and at short range by means of an inverse 12th function:

where u(r) is the intermolecular pair potential function, r the intermolecular separation, C6the dispersion coefficient, and A is a constant.
Once these extrapolations are carried out, the first iterate potential may be employed to compute its corresponding values of collision integrals using Eqs. (1)-(3) and the new inversion function through the equations similar to Eqs. (12) and (13). This new inversion function can then be used to generate a second iterate sequence of data points for the potential energy, which can in turn be employed to obtain new collision integrals. Considering the second iterate estimate for the potential energy at each separation to be closer to the true potential, this process may be repeated until convergence occurs.
The convergence criteria are judged by: (1) the extent to which the calculated collision integrals are in accordance with those obtained from experimental correlation of states, (2) the degree to which the intermolecular potential energies reproduce thermophysical properties within experimental accuracies, and (3) the degree to which the potentials are unchanged from one iteration to the next. It is worth mentioning that the rate of convergence of iterations reflects the differences of detail between the initial and the true model potentials. Fig. 1 represents the schematic diagram of the flowchart for the inversion technique.
2.3 Calculation of transport properties
The kinetic theory expressions for the viscosity, diffusion coefficient, and thermal diffusion factor in terms of collision integrals for pure gases and gaseous mixtures are given below. These formulae are appropriate under the assumption that the properties of a mixture can be determined from two-body collisions, a condition that holds for most mixtures except at high pressure, where three-body collisions can be important.

Figure 1 Schematic diagram of the flowchart for the inversion procedure
For pure species, all collisions are between like molecules so we drop the indices on εiiand σii.
2.3.1 Viscosity coefficient
Single compound
The viscosity η of a pure gas at temperature, T, is given by the kinetic theory of gases as the secondorder Kihara solution as [13]
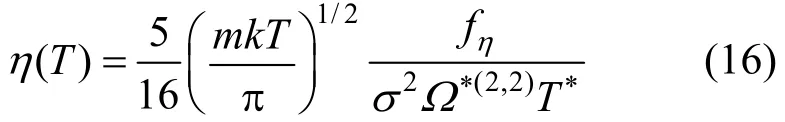
where m is the mass of a molecule and fηis a correction factor associated with the second-order solution of the kinetic theory of gases and is calculated as follows [13]
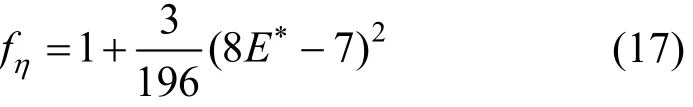
in which E∗is the ratio of collision integrals defined by Eq. (10).
Miχtures

where

2.3.2 Diffusion coefficient
Diffusion in multi-component mixtures is entirely described in terms of the binary diffusion coefficients, Dij[13],
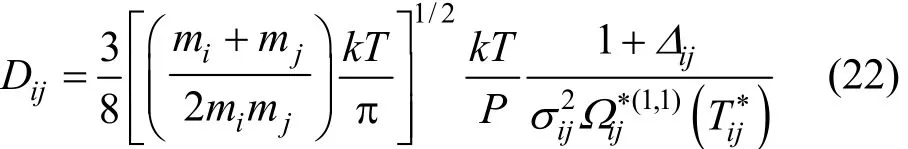
where P is the pressure and Δijis a higher order correction term of the binary diffusion coefficient, which can be defined as [13]
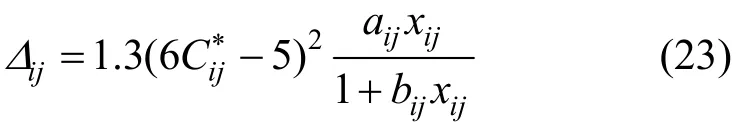
where

2.3.3 Thermal diffusion factor
When a fluid mixture is placed in a thermal gradient, one observes a separation of the components in the mixture. This separation leads to a mole fraction gradient parallel to the thermal gradient. This effect is known as the Soret effect or the thermal diffusion effect. Its amplitude is described by a phenomenological coefficient, αT, the thermal diffusion factor. The separation by thermal diffusion is usually small, but its effect can be quite important under special conditions such as in oil reservoirs [30]. An expression for the thermal-diffusion factor of a binary mixture is
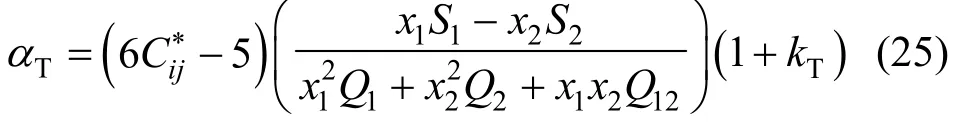
whereTk is a higher order correction term for the thermal-diffusion factor, which is usually negligible compared with experimental uncertainties in αT. The other quantities in Eq. (25) are [13]
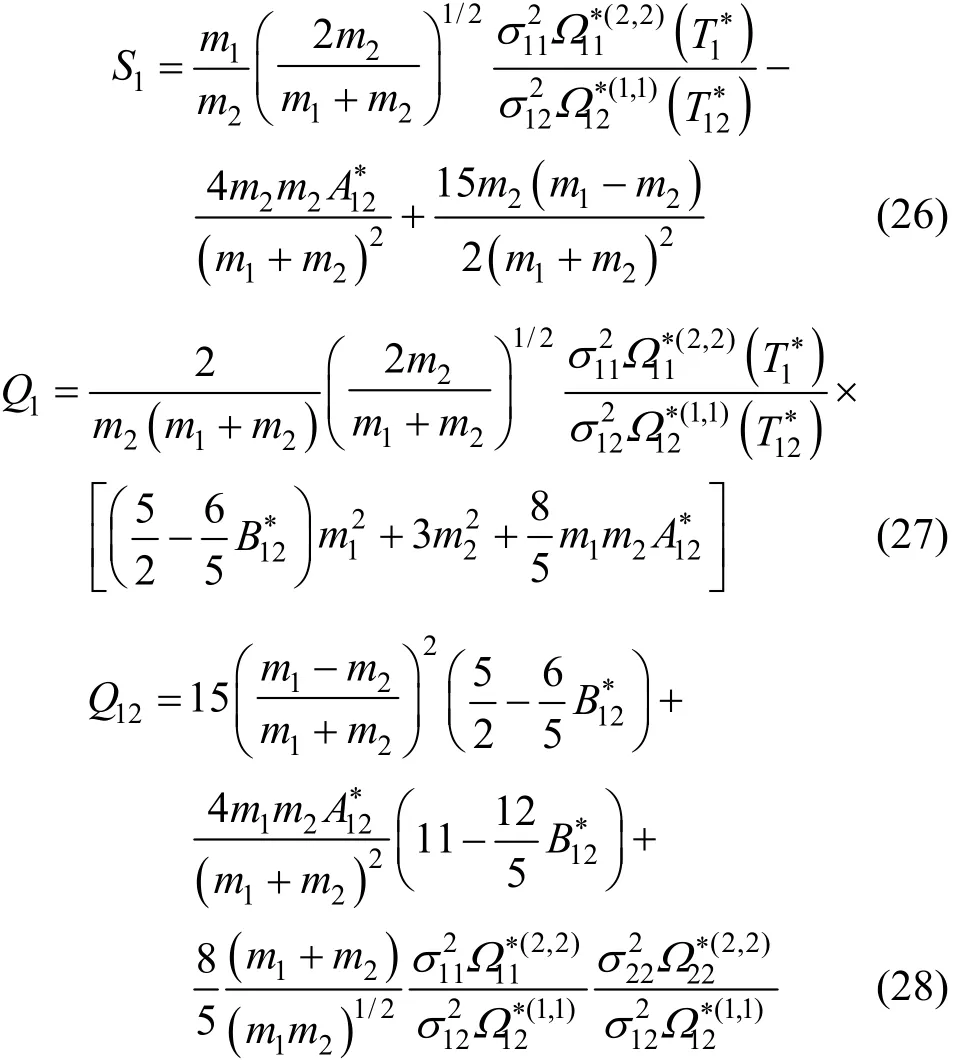
The expressions for S2and Q2are obtained from those of S1and Q1by interchanging subscripts 1 and 2. The sign convention for αTrequires that subscript 1 denotes the heavier component.
2.3.4 Thermal conductivity
The complexity of the thermal conductivity of poly-atomic molecular gases, in particular the dependence on the internal degrees of freedom and the inherent details of inelastic collisions, prevents the application of Chapman-Enskog theory to calculate this property, in which only binary elastic collisions between the molecules are considered and molecules are taken to be without internal degrees of freedom. Therefore, to calculate the thermal conductivity of the present mixtures we employ the method proposed by Schreiber et al. [31] for poly-atomic dilute gas mixtures. This scheme has been tested against the available experimental data for some non-polar mixtures [32]. Also we calculate the thermal conductivities of the studied mixtures employing Uribe et al.’s [33] method in order to compare the capability of these two methods in predicting the thermal conductivities of the binary CO2-Hydrocarbon mixtures. Uribe et al. [33] have estimated that their method will be able to predict the zero density thermal conductivity of binary mixtures, containing at least one polyatomic component, with a probable error in the order of 2%.
The thermal conductivity of a multicomponent polyatomic gas mixture at zero density can be expressed in the form analogous to that for a mixture consisting of monatomic species [31]:
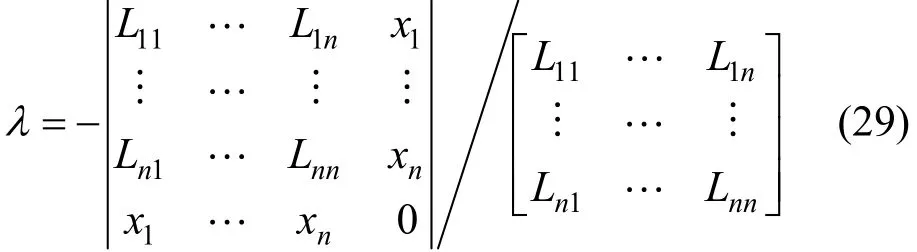
where χiis the mole fraction of species i and symbol λ, indicates the full formal first-order kinetic theory result obtained by means of expansion in Thijsse basis vectors [34]. The resulting expressions for the elements of the determinants, Lij, derived by Ross et al. [35] are complicated functions of the effective cross-sections and have little value for practical evaluation of thermal conductivity. It has been shown for pure polyatomic gases [36], atom-diatom mixtures [37], and atom-molecule mixtures [38] that accurate and relatively simple expressions can be obtained by means of the Thijsse approximation, which identifies the total energy as the dominant factor in determining thermal conductivity.
Schreiber et al. [31] applied the Thijsse approximation to poly-atomic gases and derived the expressions for the elements, Lij, in terms of measurable quantities rather than in terms of effective cross-sections. The problem was the need for knowledge of too many quantities, namely diffusion and relaxation of internal energy for different species, which were not readily available. They concluded that a further set of approximations had to be made, so they replaced all the quantities that enter the expressions for the elements, Lij, by their spherical limits. Following the application of Thijsse et al. [34] and spherical approximations to the full results, the relevant determinant elements, Lij, were given by [31]where λqis the thermal conductivity of pure molecular species q,qqλ′is the interaction thermal conductivity,is the ideal-gas isobaric heat capacity of q, R is the gas constant, and the quantities A∗and B∗are ratios of effective cross-sections given by Eqs. (7) and (8). In addition yqis the mass ratio of species q, given by

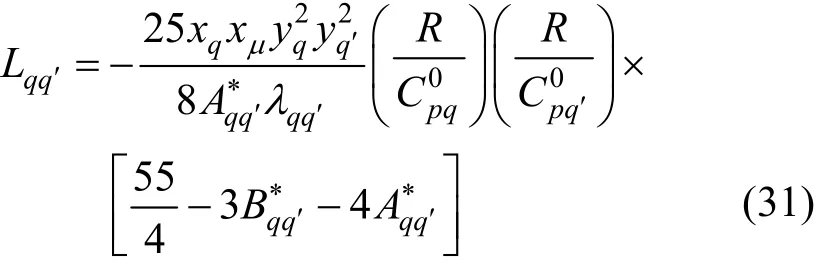
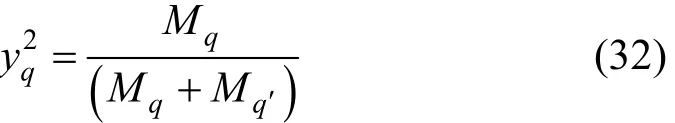
where Mqis the relative molecular mass of species q. The interaction thermal conductivity can be related to the more readily available viscosity,qqη′,

Evaluation of the thermal conductivity of a multicomponent polyatomic gas mixture thus requires the knowledge of thermal conductivity and the isobaric heat capacity of each of the pure species. This information is readily available for a large number of fluids as a function of temperature, either in terms of correlations or directly from experimental information. Furthermore, three binary interaction parameters, namely,qqη′, A∗and B∗, as a function of temperature, are also required. In the present work these quantities have been computed from the calculated interaction viscosity and collision integral ratios obtained from the inversion method.
3 RESULTS AND DISCUSSION
The interaction potential energies can be obtained via analyzing the bulk properties. The degree of success will depend on the accuracy of both the measurements and theory connecting the force to macroscopic properties, and on the sensitivity of this connection. The transport coefficients of dilute gases especially viscosity, which depends on binary interactions, satisfy the above condition. In this respect, the inversion procedure plays an important role for generating unlike effective interaction potentials from the viscosity data and their correlations of corresponding states. This, in turn, permits us to calculate collision integrals, and, consequently, the transport properties may be more accurate by correlations of the corresponding states.
The present study involves the application of iterative inversion procedure to evaluate interaction potential energy functions of the binary mixtures of CO2with some hydrocarbons, including C2H6, C3H8, n-C4H10and iso-C4H10. The resulting potentials are used to produce transport properties of these mixtures over wide temperature range in low density regime within experimental errors. The inverted pair potential energies along with Chapman-Enskog [13] version of the kinetic theory of gases and the method proposed by Schreiber et al. [31] are employed to calculate transport properties of the aforementioned mixtures.
To implement the full inversion procedure, the experimental data should be extended over as wide a temperature range as possible. In this respect, a correlation of corresponding states for the viscosity collision integrals in the temperature range ofproposed by Najafi et al. [39], is taken to calculate the reduced viscosity collision integrals. Due to the availability of accurate realistic inter-atomic potentials for noble gases, Najafi et al. derived a correlation function for, with only two potential parameters, ε and σ, based on the calculation method of O’Hara and Smith [40].
When accurate potential parameters of a gas are unknown, they can be regarded as adjustable parameters in order to give the best agreement between the calculated zero density viscosity from the Chapman-Enskog theory and the accurate experimental zero density viscosity values. Using this scheme, Najafi et al. have reported the potential parameters of some pure gases including the constituents of our studied mixtures [39]. Table 1 contains the potential parameters, ε/k and σ, for the pure species (CO2, C2H6, C3H8, n-C4H10and iso-C4H10) of the mixtures [39].

Table 1 Potential parameters for pure constituents of mixtures studied
It should be mentioned that we are confined to the calculation for 0.8T∗> , because low temperature viscosity collision integrals for molecular gases do not exist. Consequently, in order to proceed to the next iteration, it is necessary to extrapolate u(r) in the long-range region (low temperature), which enables us to integrate Eqs. (1)-(3) over the given range. Ourchosen extrapolation function is
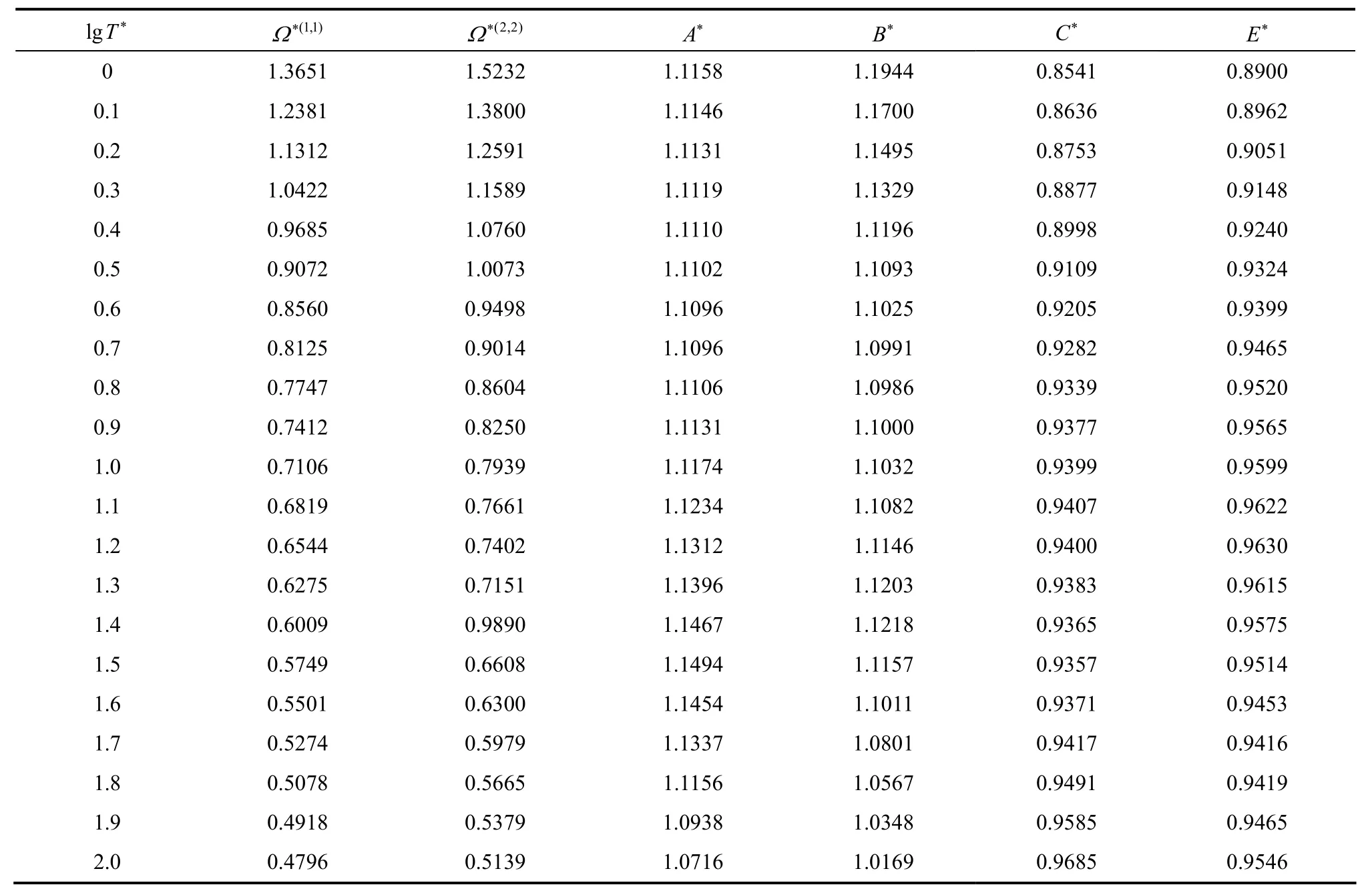
Table 2 The reduced collision integrals and their ratios for the mixtures studied

where C6is the dispersion coefficient and u is the reciprocal of the intermolecular distance, both in atomic units. The value of C6is estimated from the low-temperature viscosity data using Eq. (35). It is remarkable to mention that the inversion procedure is intensive to the nature of extrapolation function, since the potential will adjust itself during iteration steps.
Two-iterative inversion procedure, outlined previously, is applied to the calculated reduced viscosity collision integrals (from Najafi et al. correlation [39]) to generate isotropic and effective pair potential energies for the aforementioned mixtures. These potential energies are used to perform the integration over the whole range and, in turn, to evaluate the improved kinetic theory collision integrals. The results for the most commonly needed collision integrals and their ratios, obtained from Eqs. (7)-(11), are given in Table 2.
These ratios obtained from the inversion of viscosity collision integrals are expected to be of higher accuracy in comparison to those obtained from other correlations of corresponding states. Generally, calculations of other properties are considerably eased by the existence of numerical tables of collision integrals and their ratios.
The validity of any potential energy function is confirmed by its ability to reproduce thermophysical properties with acceptable accuracies. In this respect, transport properties of our four mixtures are generated from the present model potential energies. To calculate mixture transport properties we need to know binary potential parameters, σijand εij. Lack of parameters σijand εijin literature encourage us to obtain them from the like parameters, σii, εii, and σjj, εjj, using mixing rules.
Previously we have examined the effect of six different mixing rules on the calculated transport properties of some binary and ternary gas mixtures [41]. The results show that all the mixing rules are acceptable and the mixture transport properties are affected slightly using different mixing rules. However, in the case of viscosity, the results are to some extent in favor of fit MADAR-2 mixing rule [42], but this comes on the expense of two extra adjustable parameters. The Halgren-HHg mixing rule [43], which is not very successful in predicting viscosities, gives the best results for thermal conductivities. In sum, different mixing rules generally do not change the errors in the calculated properties more than ±1%. Therefore, in the present study we prefer to use the simple and famous combining rule, known as the Lorentz-Berthelot rule, in which the collision diameter is taken to be the arithmetic mean and the well depth to be the geometric mean of those for the pure species:
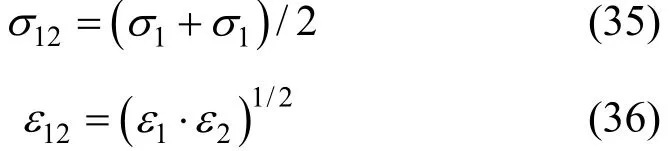
Maitland and Wakeham [44] have outlined that the experimental values of12σ agree reasonably with the prediction of Eq. (36).
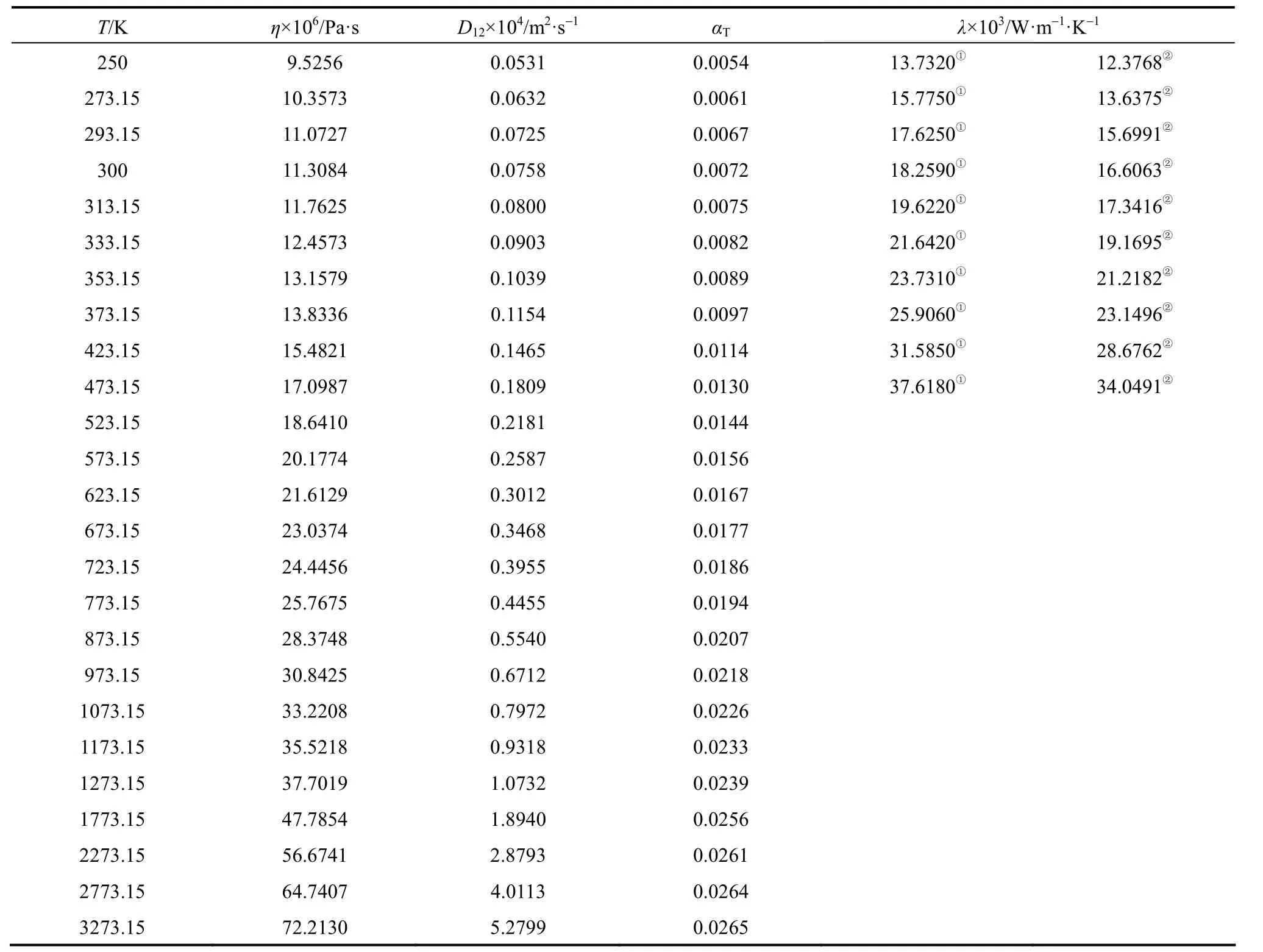
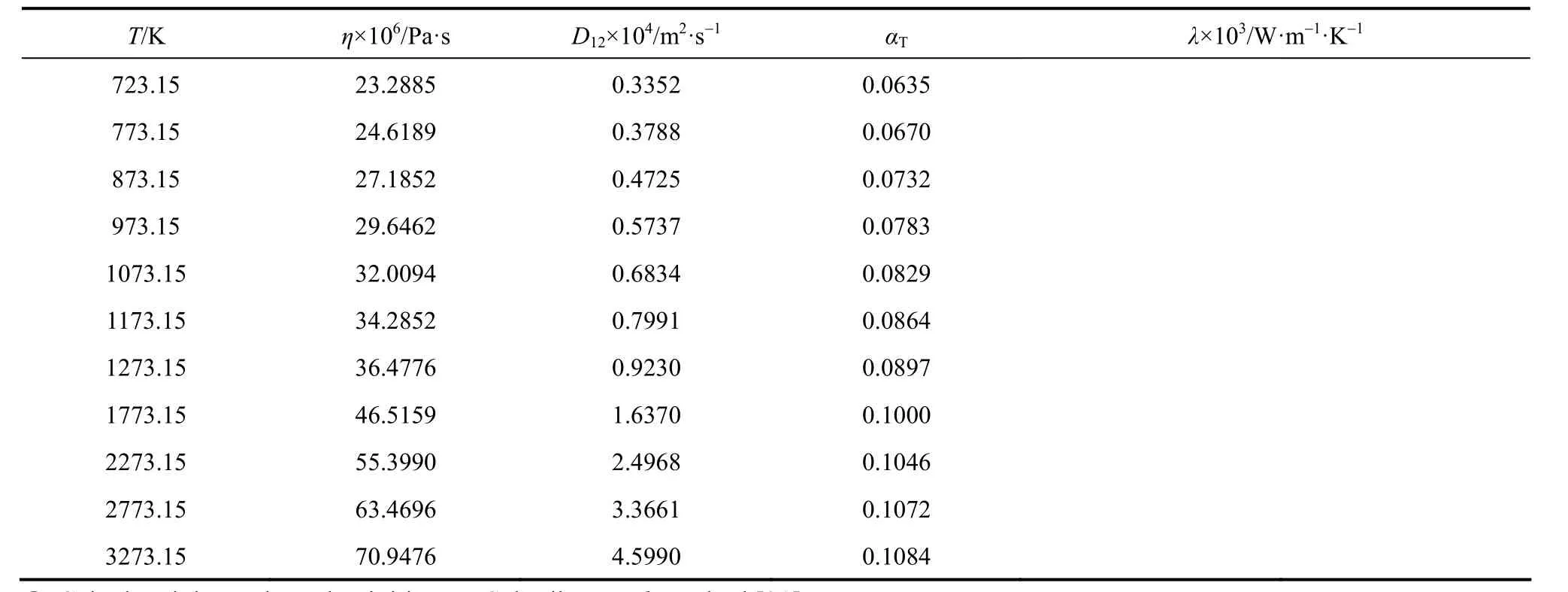
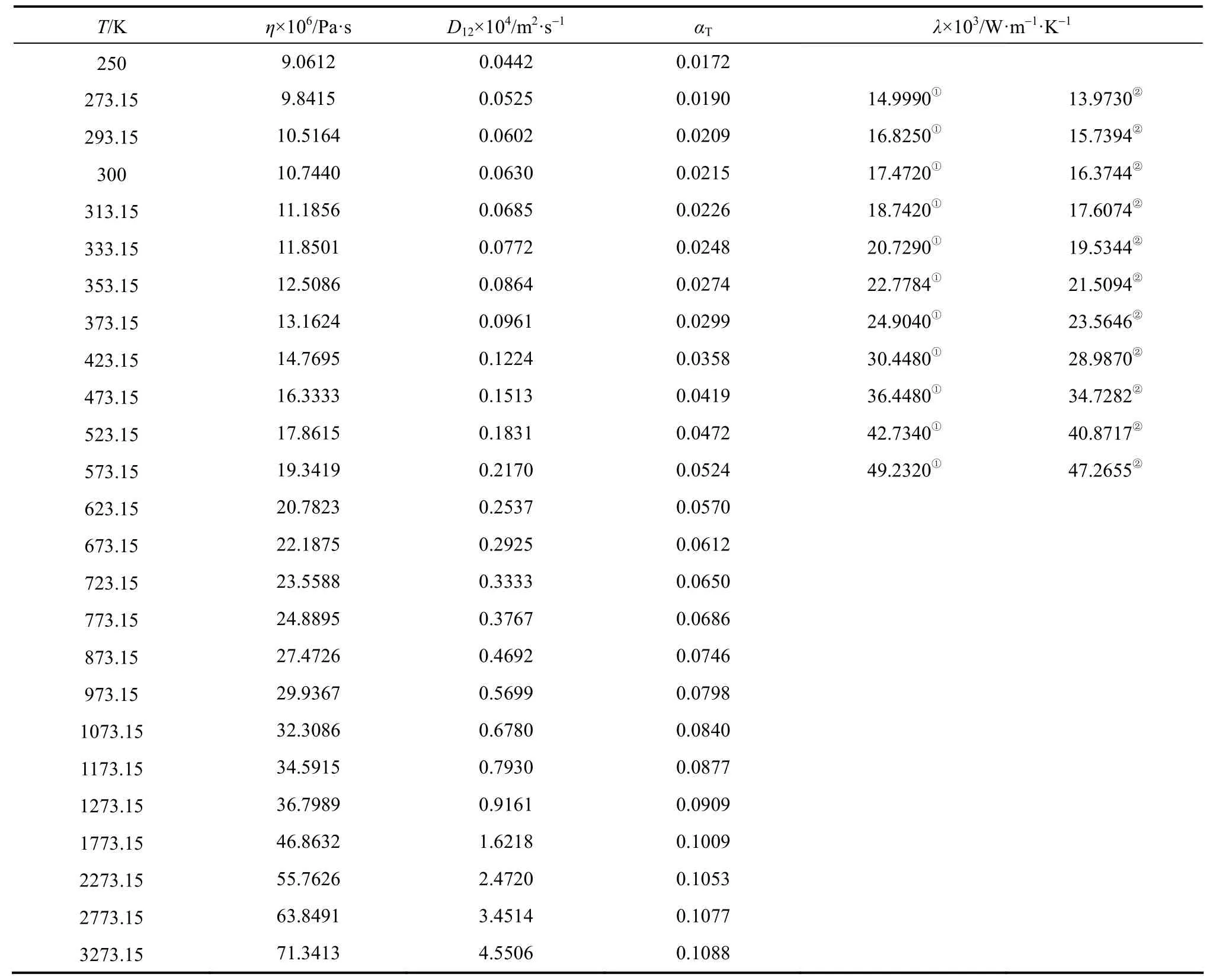
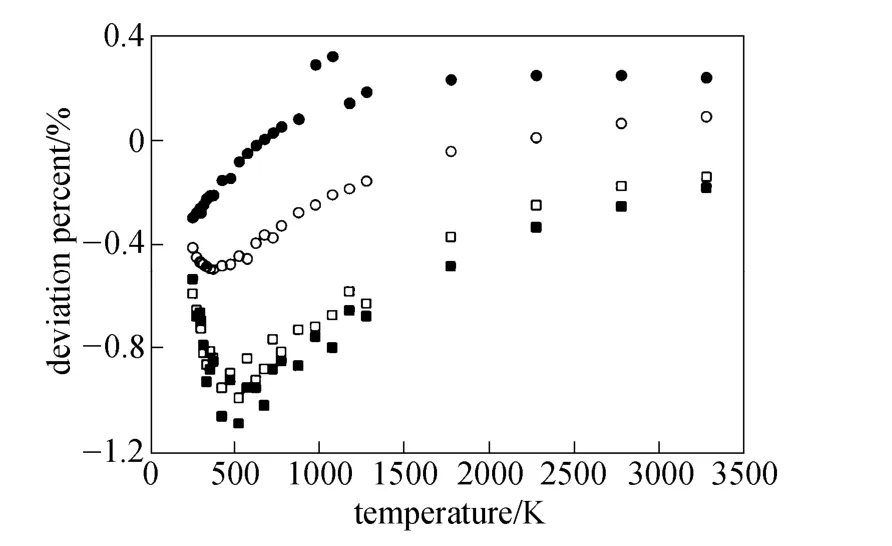
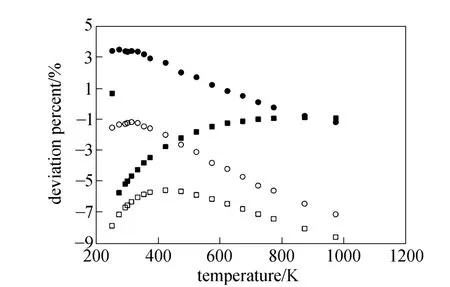
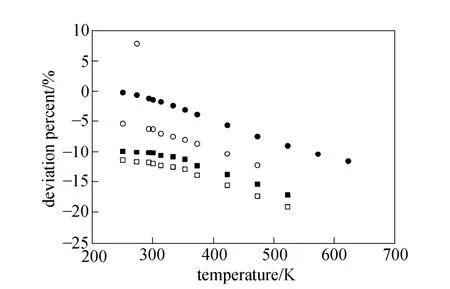
Equations (16)-(21), provided from the Chapman-Enskog version of the kinetic theory, together with the calculated collision integrals from the inverted potential energies are used to compute viscosities of the four equimolar mixtures. Tables 3-6 give the viscosity values in the temperature range 250 K where01η= μPa·s and T0=1 K . Parameters in the above equation are allowed to vary for studied systems using non-linear least squares method and listed in Table 7, with correlation coefficients (R) of the fitting contained. We compare our calculated viscosities with those obtained through Richenberg’s [45] and Davidson’s [46] methods. The former has been recommended by Poling et al. [47] as the most consistently accurate method among the other methods cited in the book. Fig. 2 illustrates the deviation plot for the calculated viscosities of the four binary equimolar mixtures from those estimated via Richenberg’s method [45]. The present results agree with this method within ±1%, which confirms the desirable harmony of the present work with this method in a broad temperature range. Average absolute deviations (AAD) from Richenberg viscosities are found to be 0.18%, 0.34%, 0.75% and 0.69% for binary mixtures of CO2-C2H6, CO2-C3H8,CO2-n-C4H10, and CO2-iso-C4H10, respectively. Fig. 3 represents the deviations from Davidson viscosities, which reveals a suitable accordance between the predicted viscosities and those given by this method. The AAD from Davidson viscosities are 0.69%, 0.35%, 0.53% and 0.34% for binary mixtures of CO2-C2H6, CO2-C3H8, CO2-n-C4H10, and CO2-iso-C4H10, respectively. These results show the reliability of our recommended potential energy models for the four mixtures and their capability for producing the viscosity coefficients with acceptable accuracies. Table 3 The predicted transport properties of equimolar CO2-C2H6mixture Table 4 The predicted transport properties of equimolar CO2-C3H8mixture Table 5 The predicted transport properties of equimolar CO2-n-C4H10mixture Table 5 (Continued) Table 6 The predicted transport properties of equimolar CO2-isoC4H10mixture Table 7 Least squares coefficients and correlation coefficients (R) for Eq. (37) Table 8 Least squares coefficients and correlation coefficients (R) for Eq. (38) Figure 2 Deviation plot for the calculated viscosity coefficients of four binary equimolar mixtures, compared with those obtained from Richenberg method [45] Figure 4 compares the calculated viscosity coefficients with those obtained using the NIST mixture property database [48]. It shows that the deviations do not exceed 6%, except for the case of (CO2-iso-C4H10) mixture. The corresponding AAD values are 2.09%, 3.12%, 2.63% and 6.68% for CO2-C2H6, CO2-C3H8, CO2-n-C4H10, and CO2-iso-C4H10mixtures, respectively. A consensus among researchers is that a method for obtaining reliable diffusion coefficients from the viscosity data is useful. The diffusion coefficients of the four CO2-hydrocarbon mixtures are calculated using the inverted pair potential energies, through their corresponding kinetic Eqs. 22-24. The numerical values of this property in different temperatures are given in Tables 3-6. For these systems, the values are correlated with the following equation Figure 3 Deviation plot for the calculated viscosity coefficients of four binary equimolar mixtures, compared with those obtained from Davidson method [46] Figure 4 Deviation plot for the calculated viscosity coefficients of four binary equimolar mixtures, compared with those obtained using the NIST mixture property database [48] Figure 5 Deviation plot for the thermal conductivities of four binary equimolar mixtures (calculated via Schreiber et al.’s method [31]), compared with those obtained using the NIST mixture property database [48] where D means diffusion, P0=1×105Pa, D0=1 cm2·s−1, and constants aD, bD, and cD, are tabulated in Table 8. The table also contains the correlation coefficients (R) of the fitting. Thermal diffusion factor, αT, is the most sensitive transport coefficient to the details of the intermolecular potential and the most difficult to measure with a high accuracy. This property describes how a gas mixture can be separated under the influence of a temperature gradient. As the value of this property increases, separation of the gas mixture becomes easier. This property is calculated for all studied binary mixtures with the help of Eqs. 25-28 and the collision integral ratios obtained from the inverted pair potential energies. Tables 3-6 represent the values of the thermal diffusion factors of the afore-cited mixtures in the temperature range. The thermal conductivity is computed using the methods of Schreiber et al. and Uribe et al. By employing Eqs. (29)-(33), which are based on the Schreiber et al.’s method [31], thermal conductivities of the four carbon dioxide-hydrocarbon binary mixtures are calculated and listed in Tables 3-6. Predicted interaction viscosities obtained from the inverted pair potential energies are employed to evaluate interaction thermal conductivities through Eq. (33). The restricted range of reported values for the thermal conductivities in comparison to other transport properties is due to the limited range of available pure species thermal conductivities and heat capacities at constant pressure, which are prerequisite for the calculation of thermal conductivities. Tables 3-6 also contain the results for the thermal conductivities obtained via Uribe et al.’s method [33]. Figure 6 Deviation plot for the thermal conductivities of four binary equimolar mixtures (calculated via Uribe et al.’smethod [33]), compared with those obtained using the NIST mixture property database [48] Figures 5 and 6 depict the deviation plots for the thermal conductivities of CO2-C2H6, CO2-C3H8, CO2-n-C4H10, and CO2-iso-C4H10binary mixtures from the NIST mixture property database [48] using different methods. Fig. 5 reveals that the AAD of the Schreiber et al. thermal conductivities are 4.52%, 7.98%, 12.01% and 13.7%, for CO2-C2H6, CO2-C3H8, CO2-n-C4H10, and CO2-iso-C4H10binary mixtures, respectively. It is clear that, as the size of the hydrocarbon increases, the deviations become greater. Calculated thermal conductivities using Uribe et al.’s method [33] present AAD values of 5.55% for CO2-C2H6, 4.02% for CO2-C3H8, 5.94% for CO2-n-C4H10and 7.52% for CO2-iso-C4H10binary mixture. The results reveal that except for CO2-C2H6mixture, Uribe et al.’s method outperforms Schreiber et al.’s method in prediction of thermal conductivity values. The present study as well as the previous work shows that inversion procedure is a powerful method for generating energy from the law of corresponding states of viscosity and a valuable supplement for obtaining transport properties, especially at high or low temperatures where direct measurements are practically difficult. In addition to the prediction of the viscosity with an acceptable accuracy, our inverted pair potential energies could be used to determine other transport properties, such as thermal conductivity with acceptable accuracies. Desirable agreement between the mixture thermal conductivities and the results from the NIST mixture property database provides a reliable test for the accuracy of the obtained potential energies. For the mixtures studied it seems that Uribe et al.’s method for thermal conductivity calculation stands over Schreiber et al.’s method. ACKNOWLEDGMENTS The work described in this paper was carried out with supports from the Shiraz University of Technology. REFERENCES 1 Welker, M., Steinebrunner, G., Solca, J., Huber, H., “Ab initio calculation of the intermolecular potential energy surface of (CO2)2and first applications in simulations of fluid CO2”, Chem. Phys., 213,253-261 (1996). 2 Zéberg-Mikkelsen, C.K., Quiñones-Cisneros, S.E., Stenby, E.H.,“Viscosity prediction of carbon dioxide-hydrocarbon mixtures using the friction theory”, Pet. Sci. Technol., 20 (1-2), 27-42 (2002). 3 Bastien, L.A.J., Price, P.N., Brown, N.J., “Intermolecular potential parameters and combining rules determined from viscosity data”, Int. J. Chem. Kinet., 42, 713-723 (2010). 4 Maitland, G.C., Rigby, M., Smith, E.B., Wakeham, W.A., Intermolecular Forces, Their Origin and Determination, Clarendon Press, Oxford (1987). 5 Clancy, P., Gough, D.W., Matthews, G.P., Smith, E.B., “Simplified methods for inversion of thermophysical data”, Mol. Phys., 30, 1397-1407 (1975). 6 Papari, M.M., Boushehri, A., “Semi-empirical calculation of the transport properties of eight binary gas mixtures at low density by the inversion method”, B. Chem. Soc. Jpn., 71, 2757-2767 (1998). 7 Papari, M.M., Mohammaed-Aghaie, D., Haghighi, B., Boushehri, A.,“Transport properties of argon-hydrogen gaseous mixture from an effective unlike interaction”, Fluid Phase Equilibr., 232, 122-135 (2005). 8 Papari, M.M., Mohammad-Aghaie, D., Moghadasi, J., Boushehri, A.,“Semi-empirically based assessment for predicting dilute gas transport properties of F2and Ar-F2fluids”, B. Chem. Soc. Jpn., 79, 67-74 (2006). 9 Moghadasi, J., Mohammad-Aghaie, D., Papari, M.M., “Predicting gas transport coefficients of alternative refrigerant mixtures”, Ind. Eng. Chem. Res., 45, 9211-9223 (2006). 10 Moghadasi, J., Mohammad-Aghaie, D., Papari, M.M., Faghihi, M.A.,“Predicting gas transport properties of light hydrocarbon mixtures as candidates for new refrigerants”, High Temp. High Press., 37, 299-316 (2008). 11 Moghadasi, J., Papari, M.M., Mohammad-Aghaie, D., Campo, A.,“Gas transport coefficients of light hydrocarbons, halogenated methane and ethane as candidates for new refrigerants”, B. Chem. Soc. Jpn., 81, 220-234 (2008). 12 Nikmanesh, S., Moghadasi, J., Papari, M.M., “Calculation of transport properties of CF4+ noble gas mixtures”, Chin. J. Chem. Eng., 17 (5), 814-821 (2009). 13 Hirschfelder, J.O., Curtis, C.F., Bird, B.R., Molecular Theory of Gases and Liquids, John-Wiley, New York (1964). 14 Chapman, S., “On the law of distribution of molecular velocities, and on the theory of viscosity and thermal conduction, in a non-uniform simple monatomic gas”, Philos. Trans. R. Soc. London Ser. A., 216, 279-348 (1916). 15 Enskog, D., Kinetische Theorie der Vorgänge in Mässig Verdünnten gasen, Ph. D Thesis, Sweden (1917). 16 Chapman, S., Cowling, T.G., The Mathematical Theory of Non Uniform Gases, Cambridge University Press, London (1970). 17 Karkheck, J., Stell, G., “Kinetic perturbation theory. Structure of collision integrals for the square-well gas”, J. Chem. Phys., 87, 2858-2866 (1983). 18 Tipton, E.L., Tompson, R.V., Loyalka, S.K., “Chapman-Enskog solutions to arbitrary order in sonine polynomials II: Viscosity in a binary, rigid-sphere, gas mixture”, Eur. J. Mech. B-Fluid, 28, 335-352 (2009). 19 Burnett, D., “The distribution of velocities in a slightly non-uniform gas”, P. Lond. Math. Soc., 39, 385-430 (1935). 20 Sone, Y., Kinetic Theory and Fluid Dynamics, Birkhauser Basel, Mumbai (2004). 21 Loyalka, S.K., Tipton, E.L., Tompson, R.V., “Chapman-Enskog solutions to arbitrary order in sonine polynomials I: Simple, rigid-sphere gas”, Physica A., 379, 417-435 (2007). 22 Lin, S.T., Hsu, H.W., “Transport collision integrals for gases using the Lennard-Jones (6, n) potentials”, J. Chem. Eng. Data, 14, 328-332 (1969). 23 Monchick, L., Mason, E.A., “Transport properties of polar gases”, J. Chem. Phys., 35, 1676-1697 (1961). 24 Herskowitz, I., Kuleshov, G.G., “Thermophysical data inversion: The limits of uncertainty”, In: Fifteenth Symposium on Thermophysical Properties, Colorado, USA (2003). 25 Maitland, G.C., Smith, E.B., “The intermolecular pair potential of argon”, Mol. Phys., 22, 861-868 (1971). 26 Gough, D.W., Maitland, G.C., Smith, E.B., “The pair potential energy function for krypton”, Mol. Phys., 27, 867-872 (1974). 27 Papari, M.M., “Transport properties of carbon dioxide from an isotropic and effective pair potential energy”, Chem. Phys., 288, 249-259 (2003). 28 Gough, D.W., Maitland, G.C., Smith, E.B., “The direct determination of intermolecular potential energy functions from gas viscosity measurements”, Mol. Phys., 24, 151-161 (1972). 29 Viehland, L.A., Mason, E.A., Morrison, W.F., Flannery, M.R., “Tables of transport collision integrals for (n, 6, 4) ion-neutral potentials”, Atom Data Nucl. Data, 16, 495-514 (1975). 30 Faissat, B., Knudsen, K., Stenby, E.H., Montel, F., “Fundamental statements about thermal diffusion for a multi-component mixture in a porous medium”, Fluid Phase Equilibr., 100, 209-222 (1994). 31 Schreiber, M., Vesovic, V., Wakeham, W.A., “Thermal conductivity of multicomponent poly-atomic dilute gas mixtures”, Int. J. Thermophys., 18, 925-938 (1997). 32 Vesovic, V., “Thermal conductivity of polyatomic dilute gas mixtures”, High Temp. High Press., 32, 163-170 (2000). 33 Uribe, F.J., Mason, E.A., Kestin, J., “Composition dependence of the thermal conductivity of low-density poly-atomic gas mixtures”, Int. J. Thermophys., 12, 43-51 (1991). 34 Thijsse, B.J., Hooft, G.W., Coombe, D.A., Knnap, H.F.P., Beenakker, J.J.M., “Some simplified expressions for the thermal conductivity in an external field”, Physica A., 98, 307-312 (1979). 35 Ross, M.J., Vesovic, V., Wakeham, W.A., “Alternative expressions for the thermal conductivity of dilute gas mixtures”, Physica A., 183, 519-536 (1992). 36 Millat, J., Vesovic, V., Wakeham, W.A., “On the validity of the simplified expression for the thermal conductivity of Thijsse et al.”, Physica A., 148, 153-164 (1988). 37 Vesovic, V., Wakeham, W.A., “Practical, accurate expressions for the thermal conductivity of atom-diatom gas mixtures”, Physica A., 201, 501-514 (1993). 38 Schreiber, M., Vesovic, V., Wakeham, W.A., “Thermal conductivity of atom-molecule dilute gas mixtures”, High Temp. High Press., 29, 653-658 (1997). 39 Najafi, B., Ghayeb, Y., Parsafar, G.A., “New correlation functions for viscosity calculation of gases over wide temperature and pressure ranges”, Int. J. Thermophys., 21, 1011-1031 (2000). 40 O’Hara, H., Smith, F.J., “Transport collision integrals for a dilute gas”, Comput. Phys. Commun., 2, 47-54 (1971). 41 Mohammad-Aghaie, D., Papari, M.M., Moghadasi, J., Haghighi, B.,“Assessment of the effect of mixing rules on transport properties of gas mixtures”, B. Chem. Soc. Jpn., 81, 1219-1229 (2008). 42 Al-Matar, A.K., Rockstraw, D.A., “A generating equation for mixing rules and two new mixing rules for interatomic potential energy parameters”, J. Comput. Chem., 25, 660-668 (2004). 43 Halgren, T.A., “The representation of van der Waals (vdW) interactions in molecular mechanics force fields: Potential form, combination rules, and vdW parameters”, J. Am. Chem. Soc., 114, 7827-7843 (1992). 44 Maitland, G.C., Wakeham, W.A., “Direct determination of intermolecular potentials from gaseous transport-coefficients alone. 1. Method”, Mol. Phys., 35, 1429-1442 (1978). 45 Richenberg, D., “New simplified methods for the estimation of the viscosities of gas mixtures at moderate pressures”, Natl. Eng. Lab Rept. Chem., 53, Scotland (1977). 46 Davidson, T.A., A Simple and Accurate Method for Calculating Viscosity of Gaseous Mixtures, U. S. Bureau of Mines, RI9456 (1993). 47 Poling, B.E., Prausnitz, J.M., O’Connell, J.P., The Properties of Gases and Liquids, McGraw-Hill, New York (2001). 48 Friend, D.G., NIST Mixture Properties Database Version 9.08 Users’Guide, National Institute of Standards and Technology, Boulder, USA (1992). FLUID DYNAMICS AND TRANSPORT PHENOMENA Chinese Journal of Chemical Engineering, 22(3) 274—286 (2014) 10.1016/S1004-9541(14)60018-5 2012-08-06, accepted 2013-04-14. *To whom correspondence should be addressed. E-mail: d_aghaie@sutech.ac.ir





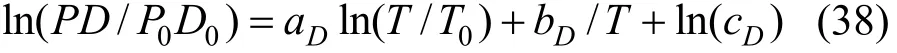

4 CONCLUSIONS
杂志排行
Chinese Journal of Chemical Engineering的其它文章
- A Contraction-expansion Helical Mixer in the Laminar Regime*
- Numerical Modeling and Analysis of Gas Entrainment for the Ventilated Cavity in Vertical Pipe*
- Hydrodynamics and Mass Transfer of Oily Micro-emulsions in An External Loop Airlift Reactor
- Effects of Shape and Quantity of Helical Baffle on the Shell-side Heat Transfer and Flow Performance of Heat Exchangers*
- Superparamagnetic Supported Catalyst H3PW12O40/γ-Fe2O3for Alkylation of Thiophene with Olefine*
- Preparation and Characterization of Sodium Sulfate/Silica Composite as a Shape-stabilized Phase Change Material by Sol-gel Method*
