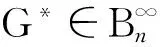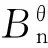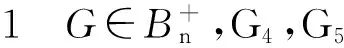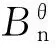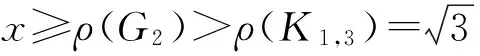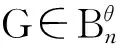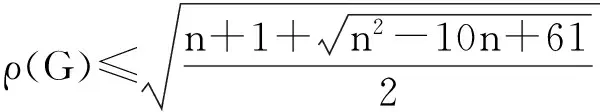不含三圈的双圈图的谱半径

何春阳

(1.青海师范大学 数学系，青海 西宁 810008； 2.盐城师范学院 数学科学学院，江苏 盐城 224002)

不含三圈的双圈图的谱半径

何春阳1，2

(1.青海师范大学 数学系，青海 西宁 810008； 2.盐城师范学院 数学科学学院，江苏 盐城 224002)

Nikiforov等人最近将图谱研究与极值图论相结合，提出了谱Turán型问题：给定一个图F，设G是一个不含子图与F同构的n阶图，那么图G的谱半径至多是多少？双圈图是边数等于顶点数加1的简单连通图。近期，部分学者对双圈图的谱半径进行了研究，确定了双圈图谱半径的第1～10大值和相应的极图。受此启发，研究了不含三圈的双圈图，确定不含三圈的双圈图的谱半径的上界，并刻画了相应的极图。

双圈图；谱半径；禁用三圈；谱Turán型问题

本文所考虑的图都是有限无向简单图，设G=(V,E)是一个n阶图，A(G)表示图G的邻接矩阵。因为A(G)是实对称的，所以它的特征根都是实数。称A(G)的最大特征根为图G的谱半径，记为ρ(G)。

经典极值图论的一个中心问题是Turán型问题：给定一个图F，设G是一个不含子图与图F同构的n阶图，那么图G的边数至多是多少？最近，Nikiforov研究了谱Turán型问题：给定一个图F，设G是一个不含子图与图F同构的n阶图，那么图G的谱半径至多是多少？当图F为n阶完全图Kr、路、圈等图时，他们分别确定了图G的最大谱半径和相应的极图，详见文献[1]。

对于一个给定的图的集合，确定该集合中图的谱半径的上界，并刻画达到该上界的图,这是Brualdi和Solheid在文[2]中提出的关于图的谱半径的一个问题。此后这个问题被广泛研究，并且获得了很多结论。边数等于顶点数加1的简单连通图称为双圈图。对于双圈图，何常香[3]确定了谱半径的前3大值和相应的极图，亓静[4]确定了谱半径的第4和第5大值以及相应的极图，王兴科、谭尚旺[5]进一步确定了谱半径的第6到第10大值和相应的极图。

受上述问题的启发，本文研究不含三圈的双圈图的谱半径，确定了不含三圈的双圈图的谱半径的上界，并刻画了相应的极图。

1 记号和引理

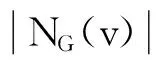
引理1.1[6]设u、v是n阶连通图G的任意两个顶点，s为某一正整数，若{v1,v2,…,vs}∈NG(v)NG(u)非空，且x=(x1,x2,…,xn)T是G的Perron向量，其中xi对应于顶点vi(1≤i≤n)。将G中的边vvi替换为uvi(1≤i≤s)，所得到的图记为G*，若xu≥xv，则ρ(G)<ρ(G*).

引理1.2[7]u是图G的一个顶点,C(u)是所有包含u的圈集合, 则图G的特征多项式满足

设Cp和Cq是两个顶点不相交的圈，v1是Cp的一个顶点，vl是Cq的一个顶点，B(p,l,q)表示把Cp和Cq通过长为l-1(l≥1)的路v1v2…vl连接而成的图(见图1)，l=1表示将v1和vl粘合成一点。设Pl+1、Pp+1和Pq+1是3个顶点不相交的路(l,p,q≥1)，P(l,p,q)表示分别将这3条路Pl+1、Pp+1和Pq+1的始点和终点粘合而得到的图(见图2)。

图1 B(p,l,q)Fig.1 B(p,l,q)

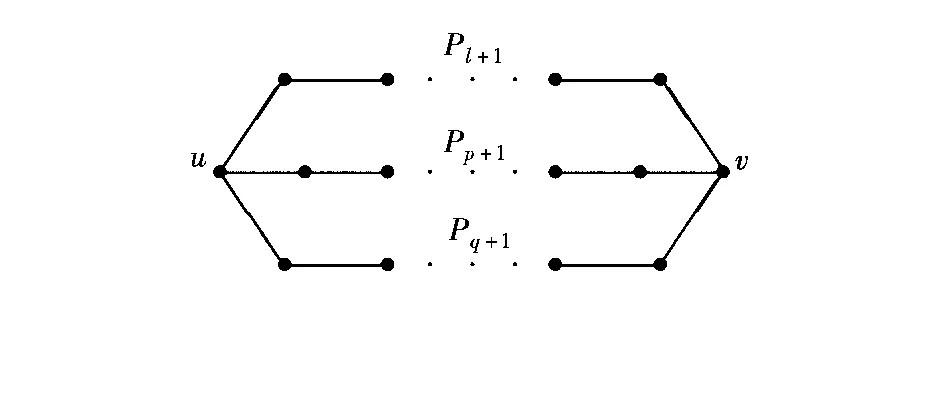
图2 P(l,p,q)Fig.2 P(l,p,q)

2 主要结果

x6-(n+1)x4+(4n-16)x2-4(n-7)=0

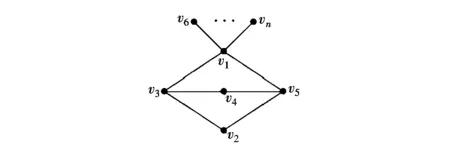
图3 G3Fig.3 G3

首先，我们证明l=1。如若不然，设l>1，v1v2…vl是连接Cp和Cq的路。不失一般性，设x1≥xl，vl+1为vl在圈Cq上的一个邻点。令

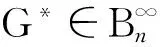
其次，我们证明G的所有树均接在B(p,1,q)的4度顶点v1上。如若不然，设B(p,1,q)的另一顶点vi上接有一棵树Ti。不妨设vi在圈Cp上，NG(vi)={vi-1,vi+1,z1,z2,…,zs}，其中vi-1、vi+1在圈Cp上。NG(v1)={vj-1,vj+1,w1,w2,…,wt}，其中vj-1、vj+1在圈Cp上。则s≥1,t≥2。如果x1≥xi，令

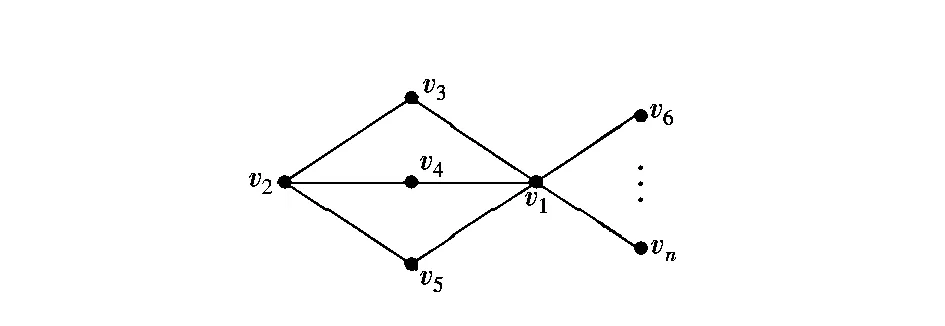
如果x1

综上可知,G是在B(4,1,4)的4度顶点上接出一些悬挂边所得到的图，即图3。对图G3的度最大的顶点应用引理1.2可得

(4n-16)x2-4(n-7)]

所以ρ(G3)为方程x6-(n+1)x4+(4n-16)x2-4(n-7)=0的最大根。

图4 G1Fig.4 G1

图5 G4Fig.5 G4

图6 G5Fig.6 G5

对图G5的顶点v1和v5应用引理1.1可得

ρ(G5)<ρ(G4)。注意到

G2=G4-v2v3+v6v3=G4-v6v5+v2v5

对图G4的顶点v2和v6应用引理1.1可得

图7 G2Fig.7 G2

对图G1和图G2的度最大的顶点应用引理1.2可得

(4n-20)x2-2n+12)

定理2.3 设n≥8，G∈Bn，则

ρ(G)≤ρ(G3)，注意到

G4=G3-v5v2+v7v2=G3-v7v3+v5v3

对图G3的顶点v5和v7应用引理1.1可得ρ(G3)<ρ(G4)。

[1] Nikiforov V. Some new results in extremal graph theory[M]. Cambridge:Cambridge University Press 2011:141-181.

[2]BrualdiRA,SolheidES.Onthespectralradiusofcomplementaryacyclicmatricesofzerosandones[J].SIAMJ.AlgebraDiscreteMethods, 1986,7:265-272.

[3]HeCX,LiuY,ShaoJY.OntheSpectralRadiiofBicyclicGraphs[J].JournalofMathematicalResearchandExposition, 2007,27(3):445-454.

[4] 亓静.n阶双圈图的邻接谱半径[J].海南师范学院学报：自然科学版,2006,19(4):289-300.

[5] 王兴科,谭尚旺.双圈图按谱半径的排序[J].数学学报：中文版,2010,53(3):469-476.

[6]WuBF,XiaoE,HongY.Thespectralradiusoftreesonkpendantvertices[J].LinearAlgebraAppl, 2005,395:343-349.

[7]ChangA,TianF,YuA.Onthespectralradiusofunicyclicgraphswithperfectmatchings[J].LinearAlgebraAppl, 2003,370:237-250.

(责任编辑：张英健)

On the Spentral Radii of Bicyclic Graphs: Forbidden 3-Cycle

HE Chunyang1，2

1.Department of Mathematics, Qinghai Normal University, Xining Qinghai 810008, China;2.School of Mathematical Sciences, Yancheng Teachers University, Yancheng Jiangsu 224002, China

Recently, Nikiforov et al., combining spectral graph theory with the extremal graph theory, proposed the spectral Turán problem : “Given a graphF, what is the maximum spectral radius of a graph of ordern, with no subgraph isomorphic toF?” When theFis complete graph, path, and cycle etc, they determine the maximum spectral radius of the graphGrespectively. A bicyclic graph is a connected graph in which the number of edges equals the number of vertices plus 1. Its spectra has been investigated widely. Inspired by the above problems, in this paper we investigate the spectral radius of triangle-free bicyclic graphs, determine the largest spectral radius together with the corresponding extremal graph among all triangle-free bicyclic graphs of order.n(n≥8)

bicyclic graph; spectral radius; forbidden 3-cycle; spectral Turán problem

2014-05-20

国家自然科学基金资助项目(11171290)

何春阳(1987-)，男，辽宁凌源人，硕士生，主要研究方向为图论。

O

A

1671-5322(2014)03-0018-04