基于冲突检查模型的机器人避障的最优路径

何改平

（1.西安外事学院 工学院，陕西 西安710077；2.西安电子科技大学 数学与统计学院，陕西 西安710071）

0 引 言

随着计算机、微电子技术的不断发展，智能机器人成为众多学者研究的热点.现有文献针对机器人的路径规划研究较多，主要分为全局和局部路径规划［1－7］，采用先进的模糊控制理论、神经元控制理论等进行路径的最优规划，算法相对复杂［8］.本文主要建立冲突检查模型，对机器人在限定区域内顺利避开障碍物的最优路径进行分析，结合MATLAB仿真计算工具，分情况进行实例计算验证了模型的正确性.

图1 不同形状障碍物平面图

1 模型假设

假设机器人在一个800m×800m场景图的原点O（0，0）处，而且它只能在该区域内活动.其内有12个使机器人不能与之发生碰撞的不同形状的障碍物，障碍物的数学描述如图1所示.

在平面场景图1中，机器人要到达障碍物外指定的目标点O（0，0），A（300，300），B（100，700），C（700，640）（目标点与障碍物之间的距离至少超过10m）.规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径.因为机器人不能折线转弯，只能通过圆弧与其相切直线或圆弧与其相切圆弧来完成转弯，所以机器人的行走路线是由直线和圆弧所构成的.而每个圆弧的半径最小为10m，且规定机器人与障碍物的最小距离为10m.若无法保证此规定，机器人会因与障碍物发生碰撞而无法完成行走.机器人直线行走最大速度和最大转弯速度分别为v0＝5m／s；v＝v（ρ）＝v0／（1＋exp（10－0.1ρ2）），其中，ρ为半径.如超过该速度，机器人将会侧翻无法行走.

（1）假设机器人可以用抽象点来说明.

（2）假设问题一中机器人经过障碍物时拐角处均是一个半径为10m圆弧.

（3）假设机器人行走过程当中均以最大速度行驶且不会出现故障.

（4）假设机器人行走速度突变时没有缓冲.

2 模型准备

2.1 冲突检查模型

冲突的检查过程，即查看路径距离障碍物的最短距离是否符合机器人距离障碍物的最短距离要求.由于路径由线段和弧线组成，现分别建立模型.

Step 1：检查路径中的所有线段是否满足距离要求，如果不满足，直接返回false.

Step 2：检查路径中的弧线是否满足距离要求，如果不满足，直接返回false.

Step 3：如果Step 1和Step 2都满足，返回true，说明该路径是一个有效的路径.

2.1.1 线段的检查 （1）线段与多边形的检查.①查看该线段的两个端点到多边形的各个边的距离是否满足安全距离要求，如果不满足直接返回false；②查看多边形的各个端点到该线段的距离是否有不满足的，如果有不满足的直接返回false；③如果①和②都满足返回true.

（2）线段与圆之间的检查.①从圆心向线段所在的直线做垂线，如果垂足落在线段上，看垂线段的长度和圆半径的差是否满足距离，如果不满足返回false；如果垂足落在线段外，计算线段上靠近垂足的点与圆心的距离，以及这段距离和圆半径的差是否满足要求，如不满足返回false；②如果①满足返回true.

2.1.2 弧线的检查 （1）弧线和多边形的检查.①查看弧线的端点和多边形的各个端点是否满足距离要求，如果不满足返回false；②从多边形的各个点向圆心做线段，如果该线段和弧线没有交点，忽略；如果该线段的长度与弧半径的差不满足距离要求返回false；③从弧心向多边形的各个边做垂线，如果垂线和弧线相交并且垂足落在边上，计算垂线段与弧半径的差是否满足距离要求，否则忽略.

（2）弧线与圆的检查.假设弧线L的半径为r1，圆O的半径为r2.①从弧心到圆心做线段L1，如果弧线L与线段L1相交，检查L1－r1－r2是否满足距离要求；②如果L与L1不相交，计算L的端点与圆O的圆心之间的距离S，查看s－r2是否满足要求.

2.2 几何模型

2.2.1 点到圆的切点距离 如图2（a）所示，设点的坐标为（a，b），如果切线斜率存在，则设为k，可得切线方程为y－b＝k（x－a），圆的方程为（x－m）2＋（y－n）2＝r2，根据圆心到切线的距离等于半径可得

其中，a，b，m，n已知，可求得斜率k，进而求得切线方程y＝k（x－a）＋b，然后将切线方程和圆的方程联立，即

解方程便可求出切点坐标（x1，x2），由两点距离公式求得点到圆的切点距离l.

2.2.2 切点到切点间圆弧的距离 用冲突检查模型准备一中的方法求出2个切点坐标，分别为A（x1，y1），B（x2，y2），若圆的半径为r，如图2所示，则弦长d和夹角θ分别为

图2 切点到切点间的距离示意图

再根据弧长公式可得弧长c

2.2.3 切点到切点之间线段的距离 （1）内公切线.如图2（B）所示，EF为内公切线，E，F为切点，设切线方程为y＝kx＋b，圆O的方程为（x－m1）2＋（y－n1）2＝r2，圆O′方程为（x－m2）2＋（y－n2）2＝r2，由圆心到切线的距离等于半径可得方程组

由方程组（7）即可解得k，b，进而得出切线方程，再与两个圆分别联立

求解方程组可解得切点D（x1，y1），E（x2，y2），根据两点距离公式得到两切点线段距离

（2）外公切线.如图2（C）所示，设圆心坐标分别为O（x1，y1）和O′（x2，y2），半径均为r，这样可以得到

那么切线方程为

由内切线算法，求出切点、切线方程，进而求得切点坐标和两切点之间的长度.

3 模型建立与求解

3.1 最短路径模型

对于任何一条机器人走的线路，其路线都是由线 －弧 －线组成，设X1，X2，…，X2n，X2n＋1分别为路径上的拐点，即直线和弧线的交点（切点）.其中奇数点和偶数点直接表示直线，偶数点和奇数点直接表示弧线，建立模型如下：

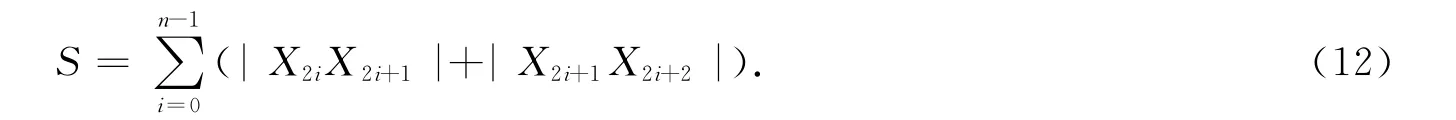
问题变成求一组能通过障碍物检验的X使得S最小.

（1）由图3得出O→A的两种路线，路径A和路径B.通过计算比较得到最短路径为路径A.设切线OX1的方程为y＝kx，利用圆心到切线距离等于半径可得

图3 O→A的两种路径示意图

其中，x＝80，y＝210，化简可得k1＝3.023 0，k2＝2.310 3（舍去）.联立切线方程和圆的方程

可得x＝70.506 0，y＝213.140 6.即切点 X1（70.596 0，213.140 6），同理得出切点 X2（76.606 4，219.406 6），现有两点 X1（70.596 0，213.140 6），X2（76.606 4，219.406 6）.根据

得c1＝rθ＝9.050 9，所以O→A的最短路径为

S1＝l1＋c1＋l2，得总长S1＝471.037 2.

（2）O→B的最短路径：从O到图形6左下角，到图形6的顶点，到图形7的右下角，到图形7的右上角，到图形8的左下角，到B.即

3.2 最短时间路径模型

由问题分析可知最短时间路径问题是在最短路径问题的基础上，考虑到速度因素，得到最短时间路径，故以拐弯半径为变量，设为ρ，从O到A由线段OX1，圆弧X1X2，线段X2A组成，设它们的长度分别为l1，c，l2，可得最短时间模型为

图4 O→B的最短路径示意图

图5 最短时间路径

（1）l1求解：设切线方程为y＝kx，圆的方程为（x－80）2＋（y－210）2＝ρ2，根据圆心到切线距离等于半径可得

经化简，据图5可得需要斜率稍大的切线，联立切线方程和圆的方程

由方程组可求得切点坐标为关于ρ的函数，即P1（x（ρ），y（ρ）），进而求得l1

（2）l2求解：设切线方程为y′－300＝k′（x′－300），圆的方程为（x′－80）2＋（y′－210）2＝ρ2，同样可求得另一个切点坐标P2（x′（ρ）、y′（ρ）），得到l2

（3）弧长c求解：由P1（x（ρ），y（ρ）），P2（x′（ρ），y′（ρ））的坐标及几何模型，可直接得到

将求得的l1，c，l2代入目标函数，解得ρ＝11.502 5时，时间最短为T＝94.564 9，且最短路径为O（0，

4 模型算法分析

文中建立的模型算法优点在于将起始点到目标点分解成多个线－弧－线模型，使得复杂问题简单化，易于实现；利用冲突检查模型结合解析几何模型优化后通过程序分别进行求解，精确度较高，便于实际检验及应用.缺点是重复计算量大，效率不高；在障碍物较多，且形状不规则时，模型需要进一步改进.针对模型中有大量重复计算的情况，可以利用MATLAB程序进行模块化编程.

机器人避障模型可以应用于电子地图路线查找，电缆及管线的铺设，交通运输等，它们都与最短路径有关，而这些问题用平常方法解决比较困难，所以可用该模型来帮助人们解决生活中的很多实际问题.

［1］李智也.移动机器人路径规划问题的解决方案 ［J］.计算机工程，2006，32（1）：189－192.

［2］金秀慧，伊连云，付莹莹，等.基于通用运动学模型的移动机器人避障路径规划［J］.机械工程师，2005，34（12）：34－35.

［3］董宇欣.移动机器人路径规划方法研究［J］.信息技术，2006（6）：108－111.

［4］王强，姚进，王进戈.基于遗传算法的移动机器人的一种路径规划方法［J］.哈尔滨工业大学学报，2004（7）：867－870.

［5］杨晶东，杨敬辉，蔡则苏.基于多目标优化的移动机器人避障算法［J］.上海交通大学学报，2012，46（2）：213－216.

［6］NUUKAEW Wuttinan，PHRUKSAPHANRAT.A fuzzy multiple objective decision making model for solving a multidepot distribution problem［C］／／Proceedings of the international Multi Conference of Engineers and Computer Scientists.Hong kong：IMECS，2010：17－19.

［7］KRUUSMAA M，WILLEMSON J.Covering the path space：A case base analysis for mobile robot path planning［J］.Knowledge－Based Systems，2003，16（5／6）：235－242.

［8］KIRBY Rachel，SIMMONS Reid，FORLIZZI Jodi.Companion：A constraint optimizing method for person acceptable navigation［C］／／The 18th IEEE International Symposium on robot and Human Interactive Communication（RO－MAN）Toyama，Japan：IEEE，2009：607－612.