大型水利工程建设项目招标设计博弈模型分析

王 梅， 王卓甫， 朱玉彩

(河海大学 工程管理研究所， 江苏 南京 211100)

大型水利工程建设项目招标设计博弈模型分析

王 梅， 王卓甫， 朱玉彩

(河海大学 工程管理研究所， 江苏 南京 211100)

我国是传统的水利大国，水利工程具有复杂性和不确定性，虽然已在初步设计阶段对工程进行了反复优化，但在招标设计阶段仍存在一定的优化空间。作为工程设计的重要阶段，招标设计的过程是业主与承包商相互博弈的过程，亦是业主对承包商进行激励的过程。本文在充分理解委托代理理论、激励理论以及博弈论思想的基础上，分析了招标设计的特点和承包商的需求，构建了业主与承包商的博弈模型。研究表明，设计一套合理的激励机制，不仅可以提高招标设计的质量，降低工程的交易费用，而且可以促进设计单位优化工程，提升工程的整体价值，具有一定的现实意义。

大型水利工程； 招标设计； 利益分配； 博弈模型

当前，我国仍处于水利工程建设的高峰期，水利工程建设投资规模不断扩大。2011年中央一号文件指出，到2020年全社会水利建设年平均投入比2010年增长一倍。2014年，国务院常务会议部署加快推进节水供水重大水利工程建设，截止2020年将分步建设纳入规划的172项重大水利工程[1]。在这一背景下，如何有效地加强水利工程投资控制是亟待有效解决的问题。根据我国现行法律、法规，水利工程设计包括，初步设计、招标设计及施工图设计。水利工程招标设计是指在可行性研究报告审查批准后，由工程项目法人组织开展，是在可行性研究报告阶段勘测、设计、试验、研究成果的基础上，为满足工程招标采购和工程实施与管理的需要，复核、完善、深化勘测设计成果的系统反映[2]。但是，考虑到大型水利工程建设项目的复杂性和不确定性，水利工程的初步设计虽然已进行了优化，但在招标设计过程中仍有较大的优化空间。同时，鉴于我国水利工程设计费的计费方式是以设计概算为基础的，设计方缺少优化工程的动力。显然，在招标设计阶段，业主的投资控制过程必然是业主与承包方相互博弈的过程，亦是业主对承包商进行激励的过程。

鉴于此，大量学者开展了研究。Ashley和Workman[3]在1986年提出激励的角色，目的是鼓励承包方优化工程目标。激励有效性的衡量标准是发包方感知的工程项目的变现和完成度。激励合约最基本的原则是：如果承包方能够有效地完成合同，那么给他获得更大利润的机会来实现其利润最大化的目标[4]。在此基础上，考虑到工程设计在工程建设中的特殊性，唐宏亮等[5]对建设工程中的建设方和设计方之间的利益冲突及其互动关系进行了博弈分析，指出需要建立一种有效的制度来规范各方的行为，而其中最重要的一点就是要符合激励相容。唐小弟等[6]指出需要设计合理有效的激励约束机制，以充分调动设计方的创造性和主动性，并且能激励设计人员精心设计，挖掘设计潜力。Kuprenas[7]对超过270个工程建设项目设计阶段的成本控制性能进行评价，通过对相关数据进行分析，认为优秀的设计团队能显著降低工程投资，并且与业主发生纠纷的事件很少。文献[3]～[6]虽然对设计阶段业主对承包方的激励展开了研究，但均是以整个设计阶段为研究对象，忽略了水利工程招标设计的特殊性，具有一定的局限性。文献[8]、[9]介绍了基于Partnering模式的博弈模型； 文献[10]通过对大型工程DB模式设计施工联动的过程分析，构建了施工单位和设计单位对设计方案更改数量的Stackelberg博弈模型，结果显示设计单位和施工单位能力、沟通和信任程度、利益共享和风险共担比例及联合体牵头人的干涉等都直接影响主体博弈行为；文献[11]建立了政府(投资)工程委托代理关系模型。上述文献分别从不同的角度探讨了工程的博弈模型，但是考虑到水利工程招标设计的特殊性，并不完全适用，仍有一定的不足。文献[12]介绍了不完全契约视角下PPP项目合作的剩余分配的博弈模型，对本文的研究具有一定的指导意义。

基于此，本文拟利用委托代理理论、激励理论以及博弈论，针对水利工程招标设计的特点、存在的问题，在充分分析业主与承包方的委托代理关系和承包方需求的基础上，构建水利工程招标设计的博弈模型。

1 招标设计的特点及需求要素分析

1.1 特点分析

工程招标设计可以推动工程设计的细化，既能提高工程招标过程中的报价或标底的可靠性，又可以降低工程的不确定性，减少施工阶段工程变更/索赔的发生。其特点详见表1。

表1 水利工程招标设计的特点

1.2 设计方需求要素分析

有效的激励约束机制必须针对设计方的需求要素，抓住设计方需求的主要矛盾。通过调研及文献总结得出设计方需求要素见表2。

表2 设计方需求要素

2 招标设计博弈模型的构建

发包方设计激励机制的根本目的主要包括两方面：(1)提升招标设计细化质量，确保合同的完备性，降低交易费用；(2)在保证质量和功能的前提下，激励设计方在招标设计过程中对初步设计进行优化，降低工程投资。

2.1 基本假设

假设1：初步设计已通过审查，并符合发包方的质量及功能要求。

假设2：参与博弈的发包方1与设计方2都是有限理性的“经济人”，可以根据自身的需求选择不同的策略。

假设3：设计方的选择：(1)选择优化或不优化，当设计方采取优化策略时，设计方会采用新工艺、新方法等对设计方案进行优化，反之，则设计方不考虑对设计方案进行优化；(2)选择努力或不努力，如果设计方采取了努力策略，那么其严格按照水利工程招标设计报告规程进行设计，确保各项数据的准确性，当设计方采取不努力策略时，设计方并未认真按照招标设计报告规程的要求对各项勘测数据认真复核。

假设4：发包方的战略选择：(1)是否采用分成合约的形式激励设计方进行设计优化；(2)是否对招标设计细化质量进行审查，当发包方采取审查策略时，可以设计一定的奖惩机制，对设计方进行奖励或惩罚，当发包方不对设计成果进行审查时，其也不会对设计方的工作态度和图纸质量进行监督评价，当发包方采取审查策略而设计方选择不努力策略时，会增加发包方的交易费用，此时设计方将受到惩罚。

假设5：设计方设计优化分成收益始终大于其为设计优化而付出的努力成本，并且当发包方采用设计优化收益分成策略时，设计方选择进行设计优化；反之，设计方不会对设计进行优化。

假设6：本模型对设计方的激励主要表现在物质报酬方面。

假设7：工程设计过程，设计方对某(子)项目优化，设计方需要对该项目重新设计，当设计优化成果/方案不能通过审查时，该风险由设计方承担；在工程设计优化方案通过审查的基础上，若该项目优化方案实施后出现风险，其主要表现为工程质量问题，则该风险由发包方承担，但发生工程变更，仍计算为设计方的差错率。

假设8：本模型只对发包方是否选择收益分成进行分析，当发包方选择收益分成时，发包方与设计方的具体博弈内容需要进一步分析。

2.2 博弈模型构建

(1)相关参数定义。假设发包方选择设计优化收益分成战略的概率为α，选择审查策略的概率为β，设计方选择努力的概率为θ(0≤θ,α,β≤1)；设计方所得设计费固定部分为I0，设计优化降低工程投资额为X，设计方设计优化收益分成所得为S；设计方进行设计优化付出成本为C1，努力工作付出的成本为C2；当发包方选择审查策略而设计方未努力工作时受到的惩罚为A；发包方对设计进行审查的费用为P1，当设计方未努力工作而给发包方造成的交易费用为P2。

(2)发包方与设计方博弈模型。

发包方与设计方的博弈模型如图1所示。

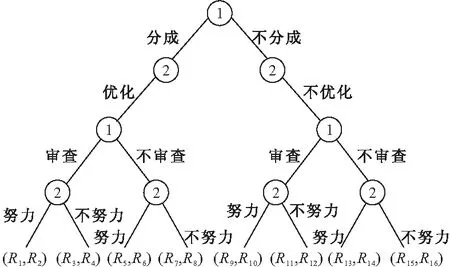
图1 发包方与设计方博弈模型

由此可得到发包方与设计方在不同策略组合下的收益如下。

R1=X-S-P1R2=I0+S-C1-C2

R3=X+A-S-P1-P2R4=I0+S-C2-A

R5=X-SR6=I0+S-C1-C2

R7=X-S-P2R8=I0+S-C1

R9= -P1R10=I0-C2

R11= -P1+A-P2R12=I0-A

R13=0R14=I0-C2

R15=-P2R16=I0

3 招标设计博弈模型分析

由上文可知，发包方的期望收益E1为：

E1={[R1θ+R3(1-θ)]β+[R5θ+R7(1-θ)](1-β)}α+{[R9θ+R11(1-θ)]β+[R13θ+R15(1-θ)](1-β)}(1-α)=Aβ-P1β-Aθβ+P2θ-P2+Xα-Sα

(1)

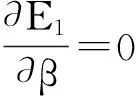
(2)

(3)

同理，可得到设计方的期望收益E2为：

E2={[R2θ+R4(1-θ)]β+[R6θ+R8(1-θ)](1-β)}α+{[R10θ+R12(1-θ)]β+[R14θ+R16(1-θ)](1-β)}(1-α)=I0+Aθβ-C2θ-Aβ+2Sα-2C1α+I0α-C2θα

(4)

(5)

在式(5)中，发包方进行审查的概率与设计方进行优化的程度成正比，与发包方采用设计优化分成策略的概率成正相关关系。这是因为当设计方对设计进行优化的程度越大时，优化后的方案与初步设计方案相比，其改变的程度就越大，进而可能会伴随着一定的风险。同时，设计方亦具有希望通过加大优化而获取更多收益的机会主义，故而，发包方只有加大审查的概率才能保证设计方为了获取更多的优化设计分成而恶意地“优化”。

工程设计优化博弈分为两个阶段：第1阶段，发包方与设计方就分配比例(或者分配比例的确定方法)达成一致意见，此阶段双方的博弈是合作性质的；第2阶段，在给定分配比例(或方法)的前提下，设计方确定对设计优化付出的最优的优化力度，此阶段存在明显的信息不对称，双方的博弈是非合作的。

3.1 优化成本分析

设计方进行招标设计的成本，概括起来可以分为两类，一类就是完成招标设计所付出的成本，称为生产性支付；另一类就是在招标设计过程中，设计方对设计进行优化，需要付出更多的智力、财力等，即优化设计创造性支付。优化设计创造性支付一般很难度量，与设计方的优化力度等密切相关。

3.2 设计方优化收益分析

基于发包方与设计方的委托代理关系，设计方的设计费用由固定酬金和激励奖金两部分组成，其中固定酬金由发包方与设计方协商确定。

激励奖金即优化设计收益分成，设计方由于付出更多的努力而使得设计方案优化，优化的产出用X表示，设计方的优化力度用p表示。设计方在优化设计过程中，受到不可抗力因素造成的设计方的损失用ε表示，根据Holmstrom和Milgrom[13]的研究，ε服从标准正态分布，即ε∈(0，1)。这里为方便起见，设计方的优化产出可线性表示为：

X=k1p+ε

(6)

式中，k1为常数。

那么，设计方参与设计工作的总收益由两部分构成，包括固定酬金和优化设计收益分成，则设计方的总收益可线性表示为：

Id=Ifix+nX

(7)

式中，Id表示设计方总收益，Ifix表示设计方固定酬金，n表示优化收益中设计方所得比例。用非线性函数表示设计方的收益也许更符合实际情况，但是根据Basu和Kalyanaram[14]的仿真研究，用线性函数表示设计方的优化力度与优化产出的关系是最佳的形式，而且线性函数表示所产生结果的差异较小。

设计方的优化设计创造性支付用C(p)表示，设计方为理性人，当p=0时，表示设计方没有受到任何激励或者设计方没有提高优化设计的积极性，而其优化设计创造性支付C(0)=0。

根据Raju和Srinivasan[15]的研究，优化产出与优化设计创造性支付呈正相关关系。为便于讨论，这里用线性公式表示优化产出。

X=k2C(p)

(8)

式中，k2为常数。

则设计方的所得利润(净收益)可表示为

Ed=Id-C(p)

(9)

那么，作为理性人的设计方，其所得总收益的期望为：

E(Ed)=E(Id)-C(p)=E[Ifix+n(k1p+ε)]-C(p)=Ifix+nk1p-C(p)

(10)

根据Holmstrom和Milgrom[13, 16]的研究，优化设计创造性支付为优化力度的非线性递增函数，为简化之便，设计方的优化设计创造性支付可表示为：

(11)

式中，a表示常数。

由式(10)和式(11)得

(12)

3.3 发包方收益分析

由于设计方的优化设计而使得投资降低，设计优化收益中扣除设计方所得部分，剩余看作是发包方的收益。这里可以表示为：

E0=(1-n)X

(13)

发包方也为理性人，发包方希望自身利益最大化，则发包方所得收益的期望为：

E(E0)=E[(1-n)X]=E[(1-n)(k1p+ε)]=(1-n)k1p

(14)

则发包方期望使得自身利益最大化，表示为

maxE0=(1-n)k1p

(15)

这里满足如下两个条件。

(1)参与约束。设计方参与优化设计的总收益不能低于预期的收益，设计方最低的预期收益用Imin表示，预期的最高收益用Imax。则参与约束可表示为：

(16)

(2)激励相容。设计方可以选择自己的优化力度而使得自身利益最大化，

所以，发包方可以采取适当的激励以促使设计方提高优化力度。则激励相容可表示为：

(17)

(18)

作为理性人，发包方不愿付出比设计方期望所获得的最低预期收益更多的费用，根据式(16)可以得出：

(19)

将式(18)带入式(19)得，发包方所愿意付出的最优固定酬金为：

(20)

通过上述分析，可以得到以下结论：

(1)由式(18)可以看出，设计方的优化力度是优化收益中设计方所得比例n的增函数，但是与固定酬金无关。结合式(8)，在给定分配比例的前提下，设计方自己决定对设计优化付出的最优的优化力度，而影响设计方进行设计优化力度的因素，还包括设计方优化设计的创造性支付。而如何设计收益分配机制，使得设计方免除对优化设计的创造性支付的顾虑，是激励机制有效运行的关键环节。

(2)由式(20)，当发包方提供的优化设计收益分配系数为0时，即n=0时，为非激励合同，设计方所得收益为发包方提供的固定酬金，此时，设计方并没有优化设计的动力。

(3)由式(20)，当发包方提供的优化设计收益分配系数为1时，即n=1，变换式(20)得：

(21)

根据激励合同，设计方的最低预期收益增大，设计方尽量提高优化力度以得到最大化的收益，但是设计方会在考虑优化成本的基础上适当选择努力水平。

4 结 论

招标设计是我国水利工程设计的重要阶段。在招标设计阶段，工程设计细化质量影响工程合同的完备性，进而影响到发包方的交易费用。此外，由于现行设计取费办法存在一定的不合理性，在招标设计过程中虽然存在一定的优化空间，但是设计方却缺少设计优化的动力。通过构建招标设计博弈模型并进行分析可知：(1)设计方的优化力度是优化收益中设计方所得比例的增函数，但是与固定酬金无关，如何设计收益分配机制，使得设计方免除对优化设计的创造性支付的顾虑，是激励机制有效运行的关键环节；(2)当发包方提供的优化设计收益分配系数为0时，即n=0时，为非激励合同，设计方所得收益为发包方提供的固定酬金，此时，设计方并没有优化设计的动力；(3)设计方尽量提高优化力度以得到最大化的收益，但是设计方会在考虑优化成本的基础上适当选择努力水平。考虑到大型水利工程建设项目招标设计的特殊性，本文在充分分析业主与承包方的委托代理关系和承包方需求的基础上，所构建的水利工程招标设计的博弈模型具有一定的现实意义。

[1] 胡亚利. 李克强主持召开国务院常务会部署节水供水重大工程建设等[EB/OL]. [2014-05-24]. http://www.mwr.gov.cn.

[2] DL/T 5212-2005，水电工程招标设计报告编制规程[S].

[3] George S. Contractual incentives [J]. Journal of Construction Engineering and Management, 1984, 110(1)：34-42.

[4] 赵宏良. 建筑工程的新型激励合同设计原理[J]. 技术经济与管理研究, 2005, (4)：56-57.

[5] 唐宏亮，陈秀丽. 建设工程中建设方和设计方的博弈分析[C]// 河南省建筑业行业优秀论文集. 北京：中国文史出版社，2006：792-797.

[6] 唐小弟, 魏 蓉. 项目业主的激励成本与设计方利益的博弈模型[J]. 中南林业科技大学学报(自然科学版), 2011, 31(6): 173-176.

[7] Kuprenas J A. Project management actions to improve design phase cost performance[J]. Journal of Management in Engineering, 2002,19(1)：25-32.

[8] 王雪青, 魏 喆. 工程管理 Partnering 模式中信任机制的博弈分析[J]. 天津大学学报(社会科学版), 2007, 9(1): 15-18.

[9] 宫立鸣. 工程管理 Partnering 模式下的合作博弈方法研究分析[J]. 中国城市经济, 2011, (23)：285.

[10]李 迁, 张劲文, 李 真. DB 模式下大型工程设计方案更改的 Stackelberg 博弈模型分析[J]. 系统工程, 2013, 31(6)：72-77.

[11]郁麒昌. 政府工程项目委托代理博弈模型[J]. 公路与汽运, 2007, (6)：151-153.

[12]安 慧, 郑寒露, 郑传军. 不完全契约视角下PPP项目合作剩余分配的博弈分析[J]. 土木工程与管理学报, 2014, 31(2)：73-77.

[13]Holmstrom B, Milgrom P. Aggregation and linearity in the provision of intertemporal incentives[J]. Journal of the Econometric Society, 1987, 55(2)：303-328.

[14]Basu A K, Kalyanaram G. On the relative performance of linear versus nonlinear compensation plans[J]. International Journal of Research in Marketing, 1990, 7(2)：171-178.

[15]Raju J S, Sinivasan V. Quota-based compensation plans for multiterritory heterogeneous salesforces[J]. Management Science, 1996, 42(10)：1454-1462.

[16]Holmstrom B, Milgrom P. Multitask principal-agent analyses: incentive contracts, asset ownership, and job design[J]. Journal of Law, Economics and Organization, 1991, 7(s1)：24-52.

Analysis on Bidding Game Model of Large-scale Water Conservancy Project

WANGMei,WANGZhuo-fu,ZHUYu-cai

(Institute of Engineering Management, Hohai University, Nanjing 211100, China)

China is one of the traditional hydraulic power country. Considering the complexity and uncertainty of water conservancy projects, although optimization has been done during the preliminary design stage over and over, there is still some room for optimization in bidding design stage. It is well known, as an important stage of engineering design, bidding design process is a process of game between the owner and the contractor. Also it is the process for the owner to motivate the contractor. Based on the principal-agent theory, incentive theory as well as the game theory, this paper analyzed these characteristics of bidding design and the demand of the contractor. Then game model between the owner and the contractor was constructed. Studies show that to design a set of reasonable incentive mechanism is very necessary. It not only could improve the quality of the bidding design which was helpful for lowering the transaction cost in the project, but also could promote the optimization level of engineering design which could enhance the overall value of the project. Therefore this study has a certain practical significance.

large-scale water conservancy project; bidding design; profit allocation; game model

2014-05-05

2014-08-22

王 梅(1991-)，女，安徽蚌埠人，硕士研究生，研究方向为工程管理(Email：dreamerwm@126.com)

中央高校基本科研业务费项目(2014B01314)；国家留学基金(201206710036)

F424.2

A

2095-0985(2014)04-0092-06