隧道火灾模型试验中参数的无量纲化研究

杨清海， 孙三祥， 李乐卓， 雷鹏帅

(兰州交通大学 环境与市政工程学院， 甘肃 兰州 730070)

隧道火灾模型试验中参数的无量纲化研究

杨清海， 孙三祥， 李乐卓， 雷鹏帅

(兰州交通大学 环境与市政工程学院， 甘肃 兰州 730070)

针对隧道火灾通风现象中众多参数复杂的相互作用特点，本文利用量纲分析的方法，对隧道火灾通风实验中火源热释放率大小与模型进行了无量纲化处理，对壁面导热过程、对流与辐射换热过程、壁面粗糙度的影响等相关参数，从量纲的角度进行了理论上的分析，比较了它们各自在隧道火灾的发展过程中起到的不同作用。最后确定了火源热释放率大小与模型是影响火源附近热力状态的决定性因素；与壁面导热、辐射过程相比，对流在火灾通风过程中起着决定性的控制作用。最后指出可以将各个参数所起不同作用的分析结果作为建立隧道火灾模型试验的理论参考，将无量纲关系式作为模型试验处理数据的依据。

隧道火灾； 模型试验； 无量纲化处理； 量纲分析

隧道火灾研究的重点在于确定火源周围温度、浓度及流场的分布，烟气扩散的规律和通风控制下流场、浓度场的相应变化。本文结合相似原理与量纲分析的方法，分析了隧道火灾模型试验中相关参数在火灾发展过程中起到的不同作用，并进行相应无量纲化处理，同时也对试验的开展进行了相应分析。

1 无量纲数确定方法

基于相似理论确定试验所需的无量纲数或者无因次准则数的方法主要有三种，即π定理法、微分方程法与量纲分析法。π定理法最直接，微分方程法最严谨可靠，量纲分析法用于对各因素的作用进行对比，找出决定性的参数，对问题进行简化。

2 隧道火灾模型试验相关准则数的确定

2.1 几何尺寸无量纲化

根据相似理论，几何相似是过程相似的基础。几何相似用数学式表达为

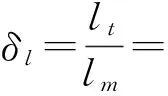
(1)

式中，lt为实际尺寸；lm为模型尺寸；δl为线性比例尺；δA为面积比例尺；δτ为体积比例尺。

2.2 火源无量纲化

π定理方法不易将火源涉及到的热释放率、对流换热，辐射换热等具有相同量纲的不同参数的作用区分开来。而且燃烧过程火焰变化极易受到影响，温度瞬变快[1]，难以用统一的微分方程来描述整个过程。

图1 控制体示意图

Thomas提出火灾的流动特征取决于浮力与惯性力即Fr数[2]。基于Thomas的结论，对图1控制体进行垂直方向上动量平衡的分析，其量纲表达式为：

(2)

式中，V为柱状控制体体积；m为流入流体质量；u为流入流体流速；ρ∞为周围冷空气密度；ρ为控制体内气体密度；A为控制体截面面积；τ为切应力；S为制体侧面面积；D为量纲比表示符号。

由于Fr数起的作用明显，对控制体动量平衡方程中的浮力项与流量动量项进行量纲的分析，即

(3)

式中，l为量纲分析时的特征长度，这里可以认为是控制体的当量直径。

由理想气体状态方程：

(4)

在定压情况下有：

(5)

式中，T∞为周围冷空气的热力学温度。

(6)

将(6)式作为量纲分析的特征速度。

分析控制体的能量平衡，量纲表达式为：

(7)

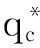
将(7)式中火源热释放率强度项与周围气体流动流量焓项相比，联立(6)式得：

(8)

式中：

Q*=mfrΔhc

(9)

式中，mfr为燃料的消耗速率；Δhc为燃料对应的化学燃烧热值。

(6)、(8)式中l可以认为是火源对应的火源尺寸。可以将火焰间歇性为50%时对应的尺寸作为火源尺寸，其与肉眼看到的相当[3]。

一般来说，隧道火灾的平均热释放率是10.5 MW。但同时，机械通风有些情况会加剧火灾的发展与蔓延。纵向通风时隧道内货车火灾热释放速率可达100 MW以上[4]。因此当通风对燃烧的影响比较大时，(8)式中的Q*用氧的消耗率来表示更加合理：

(10)

式中，mo2为氧的消耗速率；k为燃烧化学反应式中氧气与燃料的质量比。

(11)

因此得到关于时间的无量纲数：

(12)

式中，t为试验从火源开始燃烧到发展至稳定阶段所用的时间。Πt可以作为试验中火源涉及到的时间的无量纲数。

2.3 壁面条件无量纲化

壁面条件对隧道火灾过程的影响主要体现在两个方面：一是对通风气流组织的影响，二是对气流换热过程的影响，而换热过程又可分为导热、对流与辐射换热过程。

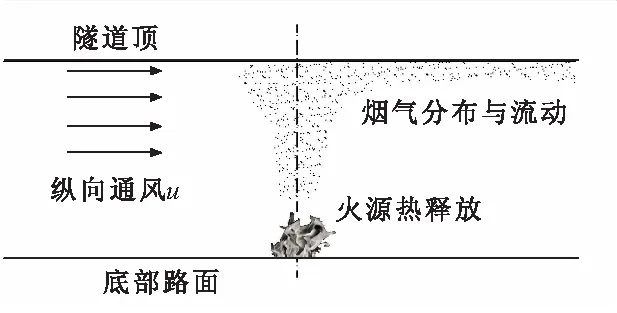
图2 隧道火灾通风示意图

2.3.1 壁面粗糙度对通风气流组织的影响及无量纲化处理

壁面粗糙度条件会改变气体流动状态与流动阻力，进而影响到通风气流的组织。黏性流体一维流动动量控制方程为：

(13)

将(13)式中惯性项与黏性项相比，惯性项与压力项相比，分别得雷诺数Re和欧拉数Eu：

(14)

式中，u为特征速度，取隧道平均速度；L为隧道横截面当量直径；μ为空气动力黏度；p为横截面的平均静压。

2.3.2 壁面传热过程分析与模型试验中的处理

隧道壁面的传热过程是一个非稳态导热过程，而且隧道的横截面并不是规则的几何结构。对壁面导热的精确计算只能通过有限差分法进行迭代求解。下面通过将隧道周围壁面作为半无限大物体，利用传热学相应原理进行非稳态导热过程的分析。设壁面温度在t=0时刻跃升为T=Tw并保持不变[6]。

半无限大物体中非稳态导热过程的控制方程为

(15)

式中，T为物体中温度变量；t为传热过程进行时长；T0为物体初始时刻温度；Tw为开始传热后的壁面温度。

温度场的分析解为：

(16)

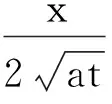
(17)

隧道火灾时，用于疏散的时间为45～60 min[7]。将ρconcrete=1930 kg/m3，kconcrete=0.79 w/(m·k)，t=3600 s，cpconcrete=1880 J/(kg·K)代入(16)式，得受影响的壁面厚度为：

(18)

(19)

可以认为在烟气的流动过程中，其传递的能量99%由周围的空气来接收，周围空气的流动对烟气流动过程的影响起决定性作用。

(20)

式中，σ为黑体辐射常数；εgas为气体的发射率；αgas为气体的吸收比；T为火源特征温度；T∞为隧道壁面温度；l为隧道当量直径。将上式作为辐射传热相关的无量纲数。

(21)

因此可以认为隧道火灾中辐射虽然对能量的传递占有一定的份额，但并不起决定性的作用，因此模型试验中选择控制无量纲数时，(20)式可以进行相应的松弛。考虑到通常只有火源附近壁面温度与烟气温度较高，相互之间辐射作用较强，在模型设计过程中应将这些部位作处理，使辐射热量不会流失在模型外周围空气中。

由此可以认为高温烟气流动过程中损失的热量绝大部分由卷吸的冷空气来承担，同时参考(18)式的结果在模型试验中可以用不需太厚、热扩散系数小的材料制作壁面，并在火源附近做隔热、不透光处理，以增加模型试验的准确性。

2.3.3 通风风速与临界风速的无量纲化处理

当通风风速达到临界风速时，由浮力驱动的烟气向上游流动动能与向下游的风的动能相抵消，即：

(22)

根据Thomas的研究及Oka的试验结果，火源附近主要由弗诺得数而不是雷诺数控制。将(22)中两项相比，根据结合(8)式的结果，风速无量纲化为：

(23)

式中，L为隧道横截面的当量直径。使用隧道当量直径而不是火源尺寸是考虑到两方面：(1)火焰产生的高温烟气在浮力作用下升至隧道顶层，之后向四周蔓延。(2)火灾规模、火源相对位置导致火焰的平均高度与隧道当量直径的相对关系的变化。火焰尺寸未达到隧道洞顶时，热力学分层不明显，羽流形成稳定[10]；火焰尺寸达到隧道洞顶时，热力学分层明显，不再形成浮力驱动的上升羽流。

3 无量纲数关系处理

首先由几何相似的原则建立隧道火灾试验所用的模型。由于Re和当量直径与特征速度的乘积成正比，如果保证模型与原型的Re相等，势必引起模型试验的速度特别大，由此可能会导致火源的燃烧机制不相同。且在火源附近弗诺得数起主要作用，因此可以放松Re的要求，保证模型处于阻力平方区即可。然后根据雷诺数Re、欧拉数Eu处理模型壁面所需要的粗糙度。通过以上的分析，将决定影响火源附近状态的无量纲数，Πh、Πt、Πv整理成函数关系：

(24)

在模型试验中通过多次改变Πt、Πh的值，并记录Πv的值，通过回归整理最终确定常数k、α、β的具体数值。

4 总 结

通过无量纲化与量纲分析，确定了隧道火灾热力过程中火源热释放率与对流过程在火灾通风中起着确定性的作用，因此热释放率、特征时间与风速的无量纲化参数，应成为指导隧道火灾模型试验开展的指导性控制无量纲数。同时，对决定性参数无量纲数之间关系的处理可以作为模型试验整理、分析数据的依据。

另外，由于隧道的长度尺寸往往比隧道的横截面尺寸多出两个左右的数量级，因此由几何相似建出的试验模型往往过于细长而失去可操作性。可以通过引入阻力隔栅增加沿程阻力，缩短隧道模型所需的长度。阻力隔栅等效的沿程长度可以通过Re、Eu的方法加以确定。

[1] 郑诗标. 公路隧道CFD建模火灾研究与实验验证[J]. 交通科技, 2014，(4)：118-120.

[2] 李颖臻,雷 波. 边界条件对隧道火灾模型试验临界风速的影响[J]. 西南交通大学学报, 2009, 44(2)：264-268.

[3] 范维澄，王清安，姜冯辉，等. 火灾学简明教程[M]. 合肥：中国科学技术大学出版社, 1995.

[4] Malhotra H J .Goods Vehicle Fire Test in a Tunnel[C]//Proceedings of the 2nd International Conference on Safety in Road and Rail Tunnels．Granada:Independent Technical Conferences Ltd,1995:237-244.

[5] 程远平,陈 亮,张孟君. 火灾过程中火源热释放速率模型及其试验测试方法[J].火灾科学, 2002, 11(2)：70-75.

[6] 杨世铭, 陶文铨. 传热学(第四版)[M]. 北京：高等教育出版社，2008.

[7] 洪丽娟，刘传聚. 隧道火灾研究现状综述[J]. 地下空间与工程学, 2005，1(1)：149-155.

[8] JTJ 026.1-1999，公路隧道通风照明设计规范[S].

[9] 陈贻来. 单个小汽车火灾热释放速率影响因素分析[J]. 消防科学与技术, 2010，29(5)：379-382.

[10]郭小平, 张启辉, 徐书林. 隧道纵向消防通风的对数理论[J].现代隧道技术, 2013, 50(2)：39-45.

Non-dimensionalization of Parameters in Tunnel Fire Model Test

YANGQing-hai,SUNSan-xiang,LILe-zhuo,LEIPeng-shuai

(School of Environmental and Municipal Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

Tunnel fire is characterised with complicate interactions among parameters of heat release rate and model, conduction and convection heat transfer, radiation and wall roughness. In this paper, the heat release rate and model were non-dimensionlized, the other parameters’ different roles in fire development were analysed with dimensional method. At last, heat release rate and model are thought as the crucial parameters to the thermodynamic process near the fire and convection plays a decisive role in the energy transfer during the ventilation process compared with heat conduction and radiation.At last, the conclusion shows that the different function roles of different parameters could be the taken as the theoretical reference and the nondimensional relation could be the guide of the data processing.

tunnel fire; model test; non-dimensionalization; dimensional analysis

2014-07-02

2014-09-23

杨清海(1989-)，男，河南开封人，硕士研究生，研究方向为隧道火灾与通风(Email:zhonguoqinghai@163.com)

U458.1； U298.4

A

2095-0985(2014)04-0103-04