多目标方法的天线相位中心计算分析

万涛，谢欢欢

（中国电子科技集团公司第二十研究所, 西安 710068）

0 引言

卫星导航系统在定位时对接收天线的相位精度要求很高，天线相位中心位置的确定和其稳定性对整个系统定位精度的影响至关重要。一些学者对天线相位中心的计算进行了研究[1-3]。当天线在主波束的要求区域内有共同的相位中心时，需要通过多个切面的远场相位数据来计算其相位中心[4]。本文通过截取天线主波束范围内的多个切面，将视在相位中心的计算转化为不同切面多目标规划的最优值问题，使用线性加权和法将该问题转化为单目标最优值问题[5-6]，最后利用差分进化算法[7]求解该区域的相位中心。通过对一个圆极化天线进行仿真计算分析，证明了该方法是切实可行的。

1 测量原理

图1中天线位于坐标原点上，其远区辐射场点p的电场分量在球坐标系下可表示为：

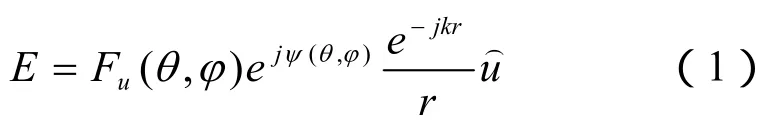
式中，Fu(θ,φ)是天线的幅度方向图是天线的相位方向图，λπ/2=k是波速。

图1 天线远场辐射示意图

天线的相位中心是指存在这样一个位置，使得其在某一频率下相位方向图),(φθΨ为常数，实际情况下是在主波束范围内相位波动很小，称这个参考位置为天线的相位中心。

在进行相位中心测量时，天线的相位中心一般情况下不可能架设的与转台旋转中心重合，这就需要采用专门的三轴调节结构根据每次测试的相位方向图调整架设相对位置，最终使得天线的相位中心与转台旋转中心重合，测量出真实的天线相位方向图。这种方法是非常复杂的测试行为，工作量巨大。

利用球面场多探头测试系统，结合优化算法，可以在一次测量的情况下计算出天线的相位中心以及相位方向图，显著提高了工作效率。该方法将转台旋转中心置于坐标原点，设转台旋转中心到天线相位中心的矢量为，则天线在远区辐射场点p的电场分量可表示为：

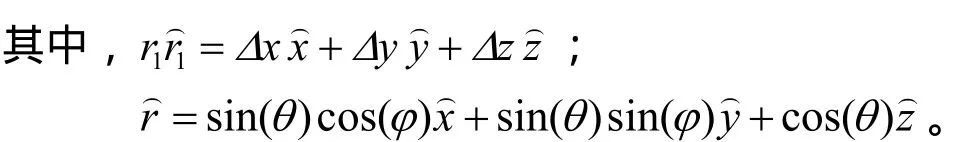
实测得到的天线相位方向图应该是：

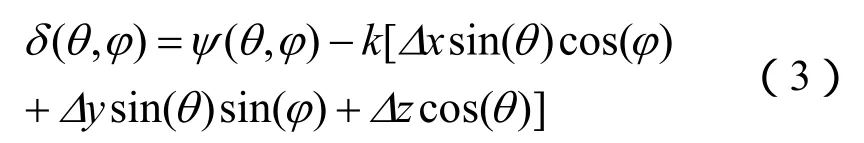
根据式（3）可求得真实的天线相位方向图Ψ(θ,φ)。天线相位中心测量就是要找到合适的相位中心位置(Δx,Δy,Δz)，使Ψ(θ,φ)波动最小。

2 多目标方法

天线相位中心是一个立体的空间位置，所以应在全空域内等φ角度地截取主波束一定范围内的p个切面相位方向图，来求解天线的相位中心，即截取的p个切面。则其相位中心求解可表示为：

fmin(Δx,Δy,Δz)表示所考查的空域内相位波动。

构造一组加权系数λi（i=1,2,…,p），使用线性加权和法将式（4）的多目标规划转化为单目标优化问题，其表达式为：

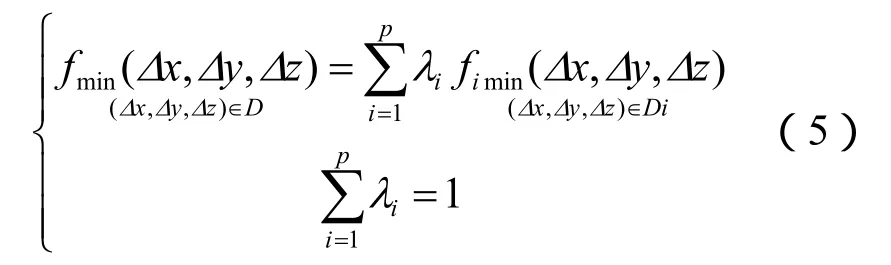
天线在主波束各切面的权重通常是一样的，因而可以取λi=i/p，i=1,2,…,p。使用差分进化算法求解式（5），即可得到该空域内相位波动最小的(Δx,Δy,Δz)值。

3 计算验证

使用HFSS软件对一个圆极化天线进行仿真及分析，用以验证计算方法的可行性。圆极化天线模型如图2所示，建模时天线相位中心故意没有与坐标原点重合。工作频率为 1.227GHz，计算其 3dBi波束宽度范围内的相位中心，并分析在该空域的相位中心稳定度。天线在φ=15o，30o，…，180o的增益和相位方向图仿真结果如图3所示。

图2 圆极化天线模型

图3 天线方向图计算结果

由图3(a)得出天线的3dBi波束宽度为±35o，因而需要寻找天线在±35o范围内的相位中心。图3(b)中天线在±35o范围内的相位不平坦，有15o左右的波动，这说明天线相位中心与这次测试转台的旋转中心不重合，存在偏差。根据测试的相位数据，使用文中提及的计算方法来计算天线相位中心偏移量 ， 计 算 得 到(Δx,Δy,Δz)=(-2.1mm, 3.8mm,22.2mm)。将天线位置移动(Δx,Δy,Δz)之后，得到天线的相位方向图如图 4所示，在波束 ± 35°范围内，天线的相位非常平坦。

图 4 移动(Δx,Δy,Δz)后天线的相位方向图

图5 ± 35°范围内天线移动前后相位方向图对比

将主波束±35o范围之内，天线移动前和移动后的相位方向图对比如图5所示。移动前，相位在8.6o到18.1o范围内变化，波动9.5o。移动后，相位在-15.4o到-14.5o范围内变化，波动0.9o，在其工作频率1.227 GHz上，其相位中心稳定度为0.3mm。

使用文献 4中两个正交主切面（取φ=90o和φ=180）进行平均的方法计算得到),,(zyxΔΔΔ=(-2.3mm, 3.5mm, 21.8mm)。在选取的切面上，文献4方法和文中的多目标规划方法计算的相位中心稳定度对比如表1所示。

表1 文中方法和文献4方法计算的相位中心稳定度对比

如表1所示，从空域所有切面来看，本文提出的多目标规划方法对天线视在相位中心位置找的更准，能获得更好的相位中心稳定度。

4 结论

本文提出一种基于多目标规划的天线相位中心计算方法。传统的计算方法通常只计算单个切面的相位中心，新方法可将空域内所用切面相位中心计算转化为基于多目标规划的最优值问题，并利用差分进化算法求解相位中心。结合HFSS仿真软件，对天线相位中心进行计算分析，验证了该方法的有效性。

[1] 毛乃宏, 俱新德等. 天线测量手册[M]. 北京：国防工业出版社, 1987: 117-121.

[2] 唐璞, 李欣, 王建, 聂在平. 计算天线相位中心的移动参考点法[J]. 电波科学学报, 2005, 20(6): 725-728.

[3] 陈曦,傅光,龚书喜,刘海风,阎亚丽. 阵列天线相位中心的测量方法研究[J]. 微波学报, 2011, 27(1): 36-39.

[4] 尚军平, 傅德民, 邓颖波. 天线相位中心的精确测量方法研究[J]. 西安电子科技大学学报（自然科学版）,2008,35(4): 673-677.

[5] 施光燕, 董加礼. 最优化方法[M]. 北京：高等教育出版社, 1999: 106-107.

[6] 薛嘉庆. 最优化原理与方法[M]. 北京：冶金工业出版社,1992: 306-311.

[7] S. Rainer, and K. Price. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces [J]. J of global optimization, 1997, 4:341-359.