非线性强陀螺效应磁悬浮转子的解耦控制

魏彤，沈繁呈

(1. 北京航空航天大学 惯性技术重点实验室，北京 100191；2. 新型惯性仪表与导航系统技术国防重点学科实验室，北京 100191)

控制力矩陀螺(Control Moment Gyro，CMG)是航天器进行姿态控制的关键执行机构[1]。与机械轴承相比，磁轴承具有无机械磨损、无需润滑、电磁力可控等优点，基于磁轴承支承高速转子的磁悬浮控制力矩陀螺(Magnetically Suspended Control Moment Gyro, MSCMG)具有高精度、高稳定性和长寿命的突出优点。然而该转子系统是一个多变量、非线性且强耦合的复杂系统，在电流和位移大幅变化的条件下，径向电磁力的非线性和陀螺效应耦合特性很强，影响系统的稳定性[2]，因此实现磁悬浮转子系统的解耦控制非常重要。

目前常用的解耦控制方法主要分为智能解耦算法与线性化解耦算法，前者主要包括神经网络解耦算法[3]、模糊解耦算法[4]、滑模解耦算法[5]等，但其需要较大的计算机资源配置，控制器设计复杂。线性化解耦方法主要包括微分几何方法[6]和逆系统方法[7]。微分几何方法虽然可以实现系统的动态解耦，但需将问题变换到几何域中讨论，且使用的数学工具复杂、抽象，系统模型受放射非线性形式的限制[8]。逆系统方法是近年来针对复杂非线性系统提出的一种常用的大范围线性化方法, 具有物理概念清晰、直观,数学分析简单明了、易于理解等优点，在线性化的过程中包含了原模型的所有项，因此克服了小范围线性化方法的缺点[9]。

文中针对MSCMG径向磁悬浮转子系统的强非线性、强陀螺效应耦合对系统稳定性的影响，提出了考虑功放环节的α逆系统结合滑模控制器的解耦控制方法，并对其进行仿真分析，从而验证该方法的解耦效果和鲁棒性。

1 非线性动力学建模

MSCMG径向磁悬浮转子提供2个平动和2个转动自由度。磁悬浮转子系统由位移传感器、控制器、功放、电磁铁和转子构成，模型如图1所示。图中只标出y方向的磁轴承，x方向与之类似，lm和ls分别为电磁铁中心和位移传感器到转子中心的水平距离；I0为Ay与Ax通道的偏置电流；usay和ucay分别为Ay通道传感器和控制器的输出电压；iay为Ay通道的控制电流；usax和ucax分别为Ax通道传感器和控制器的输出电压；iax为Ax通道的控制电流。

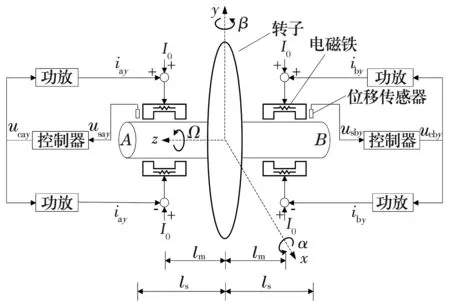
图1 MSCMG磁悬浮转子径向控制通道模型

磁悬浮转子系统的动力学模型可描述为[1]

(1)

式中：fx和fy为作用于转子质心上的外力在x和y方向上的分力；α和β为转子径向转动角位移；fax，fay，fbx和fby为转子Ax通道、Ay通道、Bx通道和By通道的电磁力；Ω为转子角速度；m为转子质量；Jx，Jy和Jz为转子在x，y和z轴方向的转动惯量，且Jx=Jy；x和y为转子质心平动位移;px为x方向的力矩；py为y方向的力矩。

电磁轴承各径向通道的电磁力为[1]

(2)

K=μ0A0N2/4，

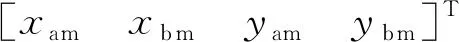
对于磁悬浮转子系统的功放环节，有

(3)

式中：u为线圈两端电压；R为线圈电阻；L为线圈电感,设a=-R/L，b=1/L，则(3)式可以表示为

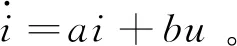
(4)

根据(1)式与(3)式可以定义状态变量X，输入变量U和输出变量Y分别为

X=[x1x2x3x4x5x6x7x8x9x10x11x12]T=

(5)

(6)

(7)

式中：u1，u2，u3，u4分别为磁悬浮转子系统4个通道的输入量。

则(1)式可表示为

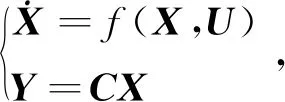
(8)

2 耦合性分析

从磁轴承坐标系到转子位置的广义坐标系的坐标变换可表示为[1]

(9)

将(9)式代入(1)式可得

(10)

式中：H=JzΩ为转子角动量，也是系统的陀螺效应耦合项。由(10)式可得径向各通道位移的二阶表达式为

(11)

由(11)式可知，当H≠0时，各通道的位移不仅取决于本通道电磁力，还受其他通道位移的影响，系统4个通道之间存在耦合，其中陀螺耦合项H随转速升高而增大，高速时成为主要耦合项。由于陀螺效应耦合项H的存在，高速磁悬浮转子在大范围偏离平衡点时，非线性强陀螺效应显著加强，一个通道的扰动会加剧其他通道的扰动，严重影响系统的稳定性。

3 α逆系统解耦模型

使用考虑功放环节的α逆系统进行解耦控制。根据(8)式可求出考虑系统功放环节的4输入4输出的状态方程，据此再建立α逆系统的解耦模型。使用α逆系统的先决条件是判断被控对象的可逆性。

首先要对输出变量Y=[xam,xbm,yam,ybm]T关于时间求导，直至输出变量显含输入变量U=[u1,u2,u3,u4]T为止。

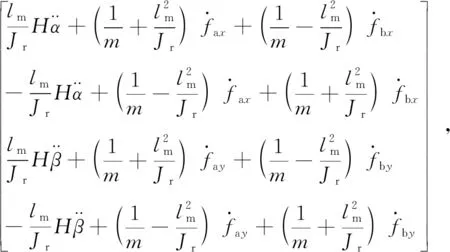
(12)

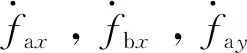
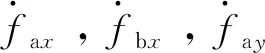
(13)

将(2)式和(12)式代入(13)式可得矩阵V的行列式为

(14)

显然(14)式的第1项不为零，而且在实际的系统中有x0>|x1+lmx2|和I0≠0，并且径向磁轴承绕组电流最大、最小值均小于I0。由此可以证明det(V)≠0始终成立。从而可以得到系统的相对阶之和为

q1+q2+q3+q4=12≤n，

式中：n为(8)式对应的系统中定义的状态变量的个数。根据逆系统理论，可判断(8)式对应的非线性系统是可逆的，即可以使用逆系统方法解耦。将该逆系统串联在原系统之前，就构成了伪线性系统。

以Ax通道为例，结合(12)式和(13)式可得系统的解析解为

， (15)

同理可求Bx，Ay和By通道的解析解u2，u3和u4。则1个具有陀螺效应耦合的非线性系统就解耦为4个简单的独立线性子系统。

4 滑模控制器设计

由于在系统建模时并没有考虑延迟和系统噪声等非线性因素，该因素形成的非线性残余耦合会影响系统的解耦效果与稳定性。滑模变结构控制适用于非线性对象，可以有效消除系统解耦后的残余耦合对系统稳定性的影响。

以Ax通道为例，假设系统输出为xam，输入为rax，考虑系统的残余耦合部分ηax，其伪线性子系统可以表示为

xam=rax+ηax。

(16)

Ax通道的滑模控制器结构示意图如图2所示，图中uax为逆系统的输入；iax为功放模型输出电流；eax为系统的误差量，且eax=rax-xam。

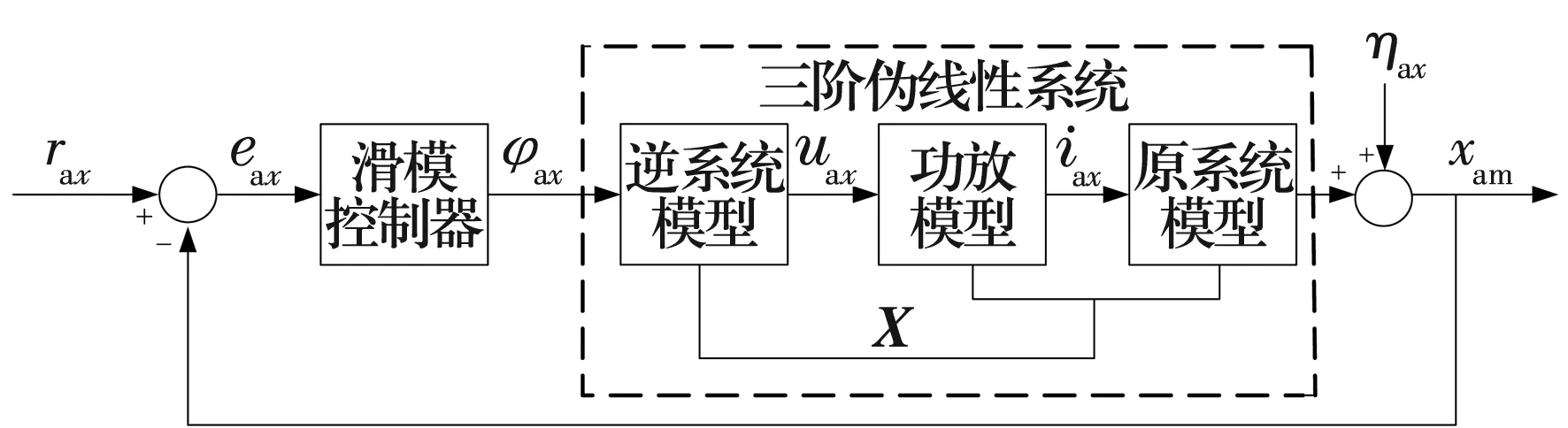
图2 系统控制框图

为了消除系统解耦后产生的残余耦合，对滑模控制器引入积分环节,设计含二阶误差导数的滑模流形面为

(17)

式中：c1，c2，c3，c4为切换函数参数，均取正数，c1一般取1[10]。当系统状态在滑模平面上滑动时，应有s=0。

对(17)式求导，并代入(16)式可得

(18)

当磁悬浮转子大范围偏离平衡点时，为使系统在短时间内可以无抖振地到达滑模态，设计指数趋近律为

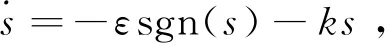
(19)

式中：ε指数为趋近律的第1个参数，取正数，决定抑制扰动及未建模动态的能力；k为趋近律的第2个参数，决定指数趋近时的速度。这2个参数保证转子受到各类非线性残余扰动而偏离滑模面时可快速返回，使系统保持良好的鲁棒稳定性。

结合(18)式和(19)式可得最终控制律为

ηax]。

(20)

由此可知，非线性滑模控制器可以消除系统解耦后的残余耦合对系统稳定性的影响，从而大幅度提高系统的解耦精确性。使用同样的方法可以设计出通道Bx，Ay和By的滑模控制器，控制系统如图3所示。

5 仿真验证

采用北京航空航天大学自主研制的单框架MSCMG的设计参数验证考虑功放环节的α逆系统结合滑模控制方法的解耦效果。为充分模拟实际磁悬浮转子的工况，在(2)式的各通道非线性动力学模型中加入模型非对称性误差ΔK，ΔI0和Δx0，使4个通道的模型不完全对称，其不对称度不超过5%，系统仿真参数见表1。

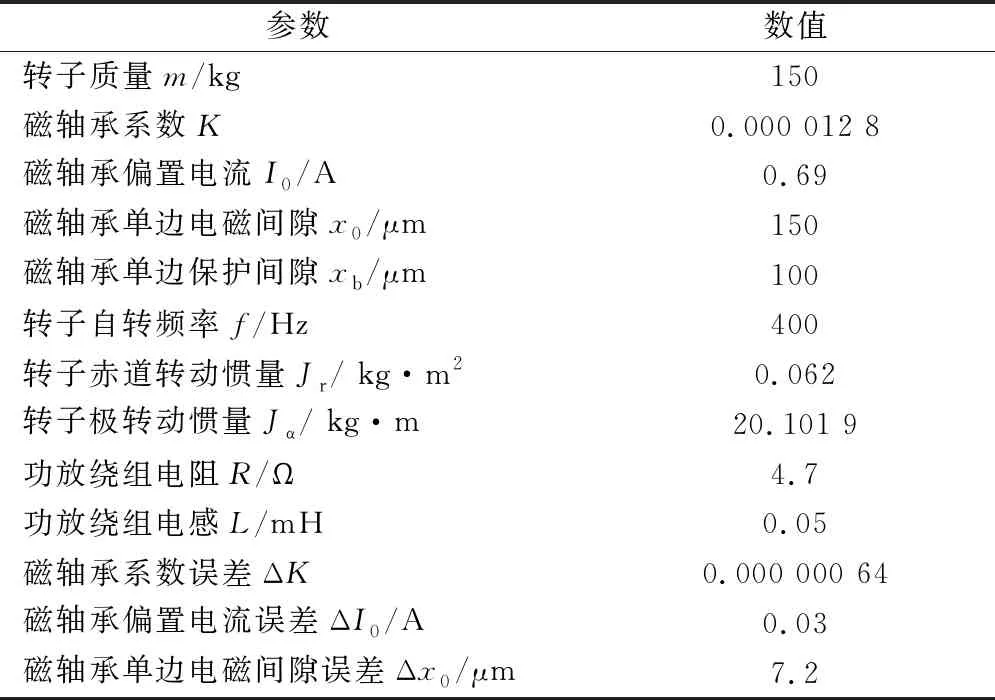
表1 磁轴承系统仿真参数

针对磁悬浮转子的强陀螺效应耦合对系统稳定性的影响，分别对基于小范围线性化的PID加交叉控制器及基于大范围线性化的考虑功放环节的α逆系统结合滑模控制器进行仿真试验。通过仿真整定，得到2种控制器的参数见表2。

表2 控制器参数

为了验证解耦效果，分别对2种控制器进行径向磁悬浮转子的解耦仿真试验，对比结果如图4所示。

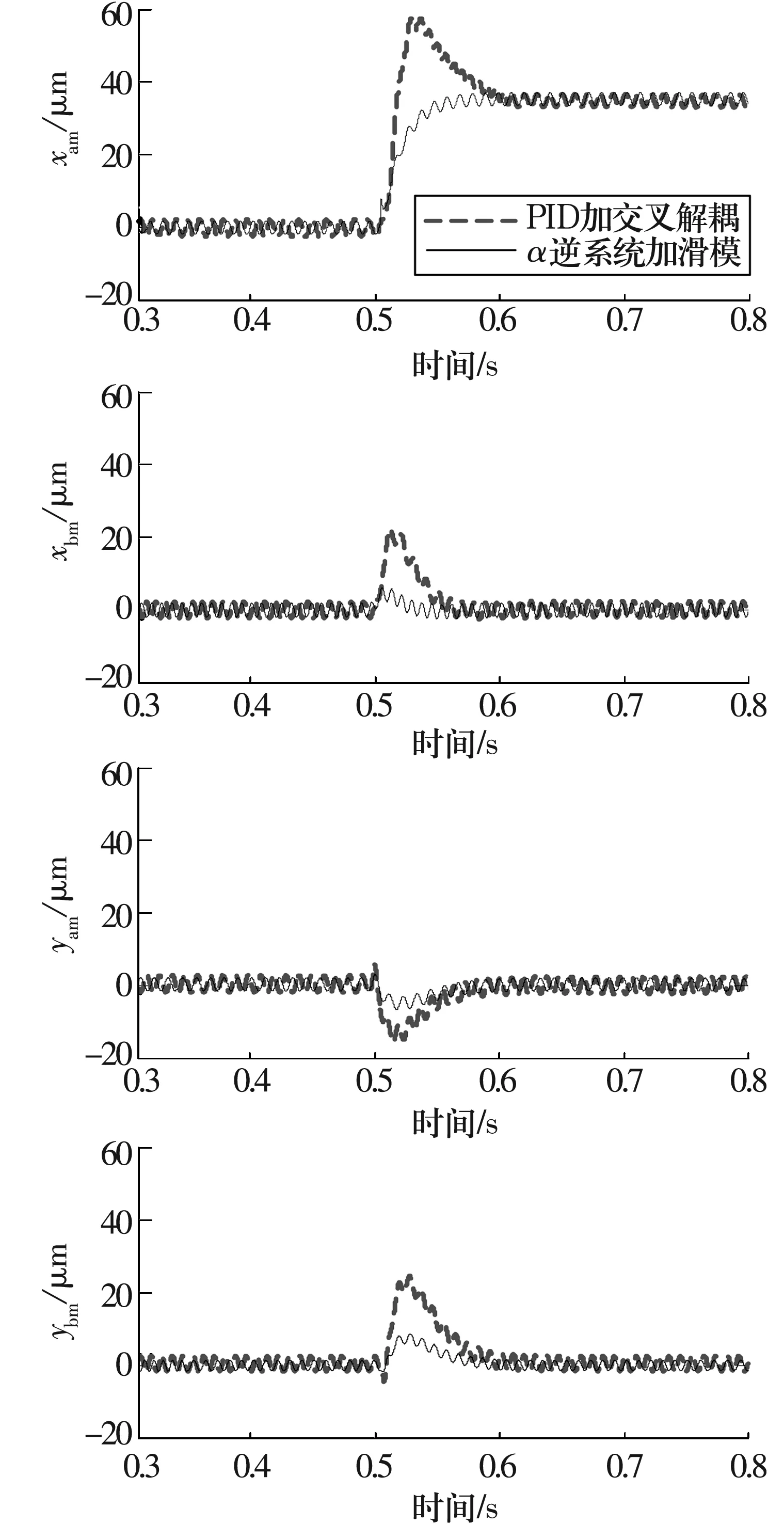
图4 PID加交叉控制与α逆系统结合滑模控制仿真结果对比

首先采用传统PID加交叉控制方法进行仿真，当t=0.5 s时，在Ax通道中加入40 μm的阶跃输入，此时Ax通道的阶跃位移对其他3个径向通道都产生了明显的扰动，Ay，Bx和By通道的偏移量分别约为20，18和22 μm，而且Ax通道有约17 μm的位移超调。这表明，陀螺效应耦合使得高速磁悬浮转子系统的动力学耦合非常强烈，当一个通道大范围偏离平衡点时，PID加交叉控制没有实现磁悬浮转子系统的解耦控制，而且系统的鲁棒性明显下降。

当采用考虑功放环节的α逆系统结合滑模控制的方法时，Ay，Bx和By通道的偏移量分别减小到了5，4和8 μm，而且Ax通道的超调量也减小到约3 μm。由于该控制方法针对完全对称系统设计，当在仿真系统中加入了模型非对称误差时，系统解耦后仍有小幅度的耦合误差。但是对比PID加交叉控制方法可知，考虑功放环节的α逆系统解耦方法具有良好的解耦效果，而且滑模控制器明显改善了系统残余耦合对稳定性的影响，从而大幅提高了系统解耦的精确性。

6 结束语

针对非线性强陀螺效应的磁悬浮控制力矩陀螺径向磁悬浮转子耦合性对系统稳定性的影响，提出了考虑功放环节的α逆系统结合滑模控制的方法，使多变量、非线性且强耦合的磁悬浮转子系统解耦为单输入单输出的伪线性子系统；进行了磁悬浮转子系统的解耦仿真试验，当系统存在5%的模型非对称性并且在Ax通道加入阶跃输入时，对比PID加交叉控制方法可知，Ax通道的位移超调量以及其他3个通道的位移跳动量均大幅减小，证明采用考虑功放环节的α逆系统结合滑模控制的方法能够实现磁悬浮转子系统良好的解耦控制。