小样本下轴承可靠性评估方法对比分析

2014-07-21高攀东陈晓阳沈雪瑾丛伟张小玲

轴承 2014年12期

高攀东，陈晓阳，沈雪瑾，丛伟，张小玲

(1.上海大学机电工程与自动化学院，上海 200072;2.苏州轴承厂有限公司，江苏苏州 215129)

随着轴承设计和制造水平的不断提高，对轴承可靠性的要求也越来越高。尤其是用于航空航天和军工等领域的轴承产品，一般具有长寿命、高可靠性的特点，由于研发和试验成本、试验周期、试验条件等各方面因素的限制，这些轴承无法进行大量试验，常进行小样本可靠性试验。

工程实践中，一般认为样本容量n<30为小样本[1]。但用在一些特殊场合的轴承产品，允许投入试验的样本量更少(n≤10)，这种情况下要选用合适的小样本数据分析方法。

目前，小样本参数估计常见方法主要有Bayes法[2]、Bootstrap法[3]、Bayes Bootstrap法[4]和Monte Carlo仿真法。自助法或随机加权法大多针对正态分布进行研究，Bayes法多用于信息融合。文献[5]提出了针对小样本定时截尾下的自助最大熵法，该方法主要进行区间估计。文献[6-7]提出了基于极大似然估计的修偏方法。文献[8]在Weibull分布小样本定时截尾情形下对最小二乘估计法、加权最小二乘估计法、极大似然估计法、基于极大似然估计法的修偏估计法和矩估计法研究后发现矩估计法优于其他方法，但其估计结果均有偏差。文献[9]在矩估计的基础上提出了中值无偏矩估计法(Median Unbiased Moment Estimation, MUME)，对矩估计法的评估结果进行一定的修偏，使之更适合于小样本数据的分析。文献[10]根据图解法原理提出了一种针对小样本数据的可靠性分析方法，即基于最小二乘法的中位秩法(The Least Square of Rank,LSR) ，该方法适用于样本量n≤20时的近似中位秩公式。文献[11]建议在样本量n≤25时采用最佳线性不变估计法(Best Linear Invariant Estimate,BLIE)，其适用于定数截尾。

下文主要针对轴承在小样本情况下(n≤10)的可靠性评估问题，将BLIE法、MUME法和LSR法进行比较分析，找到各自的适用范围，为轴承的可靠性试验数据处理寻找相对较好的分析方法，为实际应用提供理论指导。

1 Weibull分布可靠性评估

Weibull分布是寿命数据分析中应用最广泛的分布之一，大多数电子产品、机械产品等的寿命都服从Weibull分布，其分布函数为

(1)

式中：t为寿命；η为尺度参数，表示可靠度R=0.367 9时对应的寿命值，η=t0.367 9；β为形状参数，反映函数的离散程度，β值越大，函数分布越集中。由Weibull分布函数可知，其可靠度函数、概率密度函数和失效率函数分别为

(2)

(3)

(4)

根据一组小样本试验数据，估计出Weibull分布的2个参数β和η，将其代入(2)式即可算出Weibull型产品的可靠度R。Weibull分布的概率密度函数分布图如图1所示。

图1 形状参数β对分布函数的影响

由图1可知，形状参数β>1时，函数有一个峰值。根据轴承制造部门提供的数据[12]，β=1.32(ISO推荐β取1.1～1.5)；对于球轴承β=10/9，对于滚子轴承β=9/8[13]。文中的模拟参数都是基于β>1的情况。

2 小样本参数估计方法

2.1 BLIE法

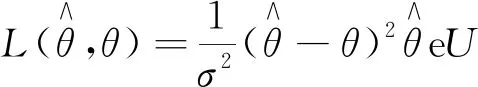
(5)

(6)

式中：n为样本容量；tin是在容量为n下的第i个试件的寿命值。

2.2 MUME法

对n个试件进行定时截尾试验，当试验进行到预先设定的截尾时间T时，得到一系列观察值t1,t2,…,tr，其中有r个数据是失效数据，而剩余的n-r个未失效数据均等于截止时间T。则根据矩估计法可得估计值为

(7)

(8)

(9)

(10)

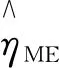
(11)

2.3 LSR法

该方法的本质是图解法，即将失效数据运用中位秩法求得失效率后，再利用最小二乘法对数据进行回归分析，从而得到小样本下的可靠性评估。其原理是将Weibull分布函数经过一系列的变换后，把ti～F(ti)的关系转变成xi～yi的关系。应用LSR进行Weibull可靠性分析过程与传统的应用Weibull概率纸处理数据的过程类似，其分析步骤如下：

(1)将失效时间ti(广义)按从小到大顺序排列；

(2)将数据进行预处理，令xi=lnti；

(5)数据点[ti，F(ti)]变为[xi,yi]，应用LSR法拟合该组数据；

(6)得出分布函数的2个参数估计值β和η。

文中采用文献[11]中的近似中位秩公式进行计算。

3 3种方法的对比分析

BLIE法是基于定数截尾提出的，而MUME法是基于定时截尾的，LSR法两种情况都适用。因此要统一三者的适用条件才能进行对比分析。

3.1 定数截尾与定时截尾

在一定的样本容量和分布母体下，使某一样本结构出现最大概率的截尾时间为某一区间上的任意值[8]。如果试验中的定时截尾时间在该区间内，则定时截尾与定数截尾是统一的。当试验选定失效数时，对应的定时截尾时间也就确定了，反之亦然。在该情况下的试验数据符合3种分析方法，下文Monte Carlo模拟仿真基于这一结论进行。

3.2 Monte Carlo模拟试验及结果对比分析

选取样本量n=4，6，8和10分别对3种方法进行Monte Carlo模拟试验，仿真选取形状参数和尺度参数为β=3，η=10 000。为了比较不同方法的优劣，采用高可靠度范围内的k个检测时刻的可靠度估计值与真值(可靠度值在[0.9,1]内)进行比较，记为

(12)

护士应叮嘱患者在术前6小时，禁食禁水，使胃肠道处于排空状态。在术前3小时，禁止患者服用抗凝药物，以免在术中出现血流不止现象，增加手术患者的风险。此外，还应对手术患者进行常规备皮准备，并详细向患者讲解心脏起搏器工作原理以及治疗方案，取得患者的理解的配合，提高手术治疗效果。

参数估计值β=3，η=10 000，样本量n=10时，不同失效数r下3种方法的评估结果对比如图2所示。

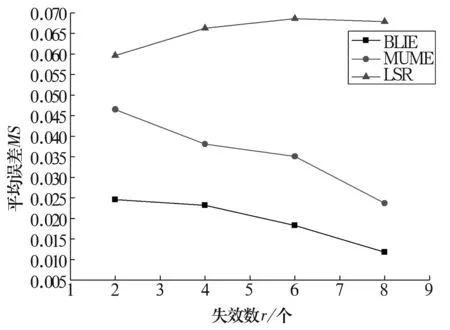
图2 评估结果随失效数r变化的情况对比

由图2可知，失效数相同时，BLIE法的估计结果最优，MUME法次之，LSR法最差。样本量相同时(n=10)，随失效数的增加，BLIE法和MUME法的评估结果越来越好，而LSR法的误差却有增大的趋势。以MS≤5%作为评价指标，BLIE法和MUME法的评估结果均合格，LSR法的评估结果不合格，因此，当样本量n≤10时，LSR法不适用。

当失效数r一定(r=4，即T=8 000 h)时，3种方法的评估效果随样本量变化的规律如图3所示。

图3 评估结果随样本量n变化的情况对比

由图3可知，当失效数r不变时，3种方法的平均误差均随样本量的增加而减小。以MS≤5%作为评价指标，BLIE法适用于n>6的情况，MUME法适用于n≥8的情况，当样本量n≤10时，LSR法仍不适用。LSR法是基于数据点进行曲线拟合，如果失效数或者样本量较少，则拟合效果差，导致评估结果差。

3.3 参数变化时的评估结果对比分析

为了说明分析规律的一般性，现将Monte Carlo模拟参数变为β=1.5，η=4 000。两种情况下的截尾时间分别为4 000 h和10 000 h，样本量n=8，失效数r=6，仿真及计算过程均同上，Weibull分布参数变化时的评估结果规律见表1。

表1 不同参数下3种方法的评估结果对比

由表1可知，当参数变化时，3种方法的评估结果及规律不变，BLIE法最好，MUME法次之，LSR法最差。随着参数的增大，3种方法的分析误差均随之增大，但仍是BLIE法的误差最小，MUME法次之，LSR法最大。

如果还以MS≤5%作为评价指标，在Weibull参数较小的情况下，3种方法适用的最小样本量更小。对于一批给定的轴承，先大致确定Weibull分布参数的取值范围，从而确定最小样本量。

3.4 极小样本情况下的对比

为了找到更适用于极小样本下的可靠性评估方法，取模拟参数(β，η)为(2, 4 000)，样本量n=5，仿真及计算过程同上，3种方法的评估结果见表2。

由表2可知，在极小样本下，3种方法的评估效果及规律仍同前文所述。由于参数变小，BLIE法在样本n=5时也满足MS≤5%，另外两种方法的误差仍然较大。

表2 极小样本下3种方法的评估结果对比

4 实例分析

已观测到5套陀螺电动机转子轴承的失效时间由小到大依次为1 313,2 288,2 472,2 506,3 382 h[15]。按前文所述的方法将数据处理成定时截尾数据，同时满足定数截尾。取定时截尾时间为3 000 h，即失效数r=4。分别用3种方法处理上述数据，并将完全样本数据用极大似然估计法处理，3种方法的估计结果与极大似然估计结果对比见表3，其中，极大似然的估计结果为β=4.168，η=2 637.18。