单片机和FPGA实现的多混沌吸引子切换系统

张建广，康守强，纪斌，宋立新，郑势，朱建良

1.哈尔滨理工大学电气与电子工程学院，哈尔滨 150080

2.中国移动通信集团黑龙江有限公司网络管理部，哈尔滨 150028

单片机和FPGA实现的多混沌吸引子切换系统

张建广1，康守强1，纪斌1，宋立新1，郑势2，朱建良1

1.哈尔滨理工大学电气与电子工程学院，哈尔滨 150080

2.中国移动通信集团黑龙江有限公司网络管理部，哈尔滨 150028

1 引言

混沌作为一种复杂的非线性现象，过去的几十年里在科学及工程应用等领域得到了极大的关注。目前国内外的相关文献已经报道了许多由模拟电路[1-3]或数字电路[4-8]产生的混沌系统，它们在不同的应用领域存在不同的优缺点。但模拟电路对元件固有参数及信号的再生误差很敏感，使得混沌通信中对混沌状态的控制和同步比较困难。

多混沌吸引子切换系统，因其系统随机性强，可产生更加时变、多样和复杂的混沌信号，提高其应用的效果。例如可提高混沌信息加密的安全性，且其抗破译能力强于一般的混沌系统[9]。研究多混沌吸引子切换系统具有重要的理论和实际应用价值[10-11]。

目前有文献报道实现了切换混沌系统，方法不尽相同。实现切换混沌系统可以利用变参数切换的方法、变结构切换方法。统一混沌系统是利用变参数切换的方法实现的，随着参数的改变，系统在Lü系统、广义Lorenz系统、广义Chen系统之间切换[12-13]。文献[10]采用系统选择器、模拟开关的手动切换，通过模拟电路能实现多个关联子系统的功能；文献[6]通过修改混沌系统中的非线性项，构造开关函数，使函数变量取不同值时非线性项不同，构成了开关混沌系统；文献[14]利用两相信号正负来决定系统的非线性项，结合模拟开关控制，实现多个子系统组成的自动切换的混沌系统。无论是变参数的切换、变结构的切换还是二者相结合，都可以依赖于时间的切换。文献[15]构建了一个切换四涡卷超混沌系统，系统以时间依赖切换来选择不同的混沌子系统，通过人为操作模拟电路中控制开关K选择线性不同的反馈项，实现子系统随时间切换的功能。

本文利用单片机控制FPGA实现了不同混沌系统吸引子的产生和快速分时切换，即采用数字电路，在一个电路系统中实现多个混沌系统，并可实现不同的混沌系统间及系统的不同变量之间的随机和快速分时切换，增加了混沌信号的多样性、时变性、选择性和灵活性。不同的混沌系统切换相比改变某个参数或变量的混沌子系统切换所形成的整体混沌信号具有差异性大的特点。因此，也增加了混沌信号的复杂性。

2 混沌数学模型及离散化

为了用FPGA构造混沌系统，首先利用快速数字差分算法将混沌系统的连续微分方程组转换为离散的差分方程组。采用快速的Euler算法，用离散化公式（1）对连续混沌方程进行离散化，将微分方程组转化为差分方程组：

2.1 Lorenz混沌系统

Lorenz混沌系统的微分方程描述为：

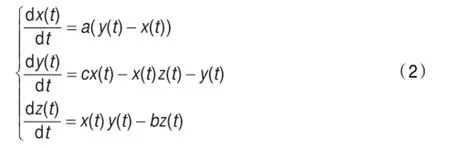
其中，a=10、b=8/3、c=28，初值为x(0)=1、y(0)=1、z(0)=1时，该系统为复杂的混沌系统。

由式（1）可知，Lorenz混沌系统对应的差分方程组为：

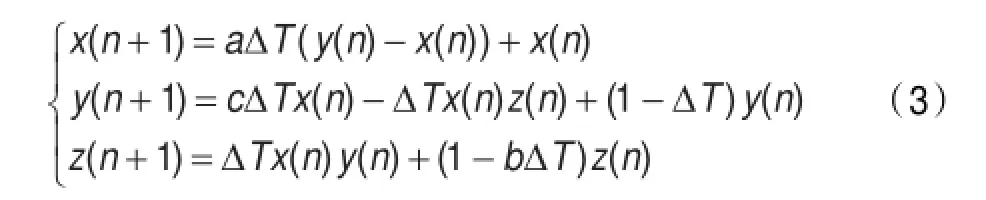
当ΔT取足够小时，式（2）和式（3）具有相同的动态特性。这里取ΔT=0.000 05[7]，则式（3）变为：

2.2 四维超混沌系统

2008年王忠林等人提出了一个四维的超混沌系统[16]，四维超混沌系统的微分方程描述为：

其中，a=10、b=2.5、c=4、e=0.25、g=2，初值x(0)=1、y(0)=1、z(0)=1、w(0)=1时，该系统为复杂的超混沌系统。

同理四维超混沌系统对应的差分方程组为：

3 离散混沌模型的仿真

利用MATLAB结合DSP Builder进行波形仿真，首先根据式（4）建立Lorenz混沌系统对应DSP Builder中的系统框图。如图1所示为Lorenz混沌系统对应的DSP Builder结构框图。

图1中PLL为锁相环，通过设置可以实现对输入时钟的分频或倍频。本文利用锁相环电路对输入时钟进行10分频，用于DAC模块的时钟输入。如图2所示是Lorenz混沌系统部分吸引子在DSP Builder中的仿真相图。

同理可根据式（6）建立四维混沌系统对应DSP Builder中的系统框图及对应的结构框图。该混沌系统部分吸引子在DSP Builder中的仿真相图如图3所示。上述仿真均说明各混沌系统的离散模型正确。

4 多混沌吸引子分时切换系统的设计

本系统以Lorenz混沌系统（记为s1，j）和四维超混沌系统（记为s2，j）作为分系统，分时切换输出：

式中，i=1,2，时间段t1，j对应Lorenz混沌分系统s1，j（j表示该系统的不同变量，j=1，2，3）；时间段t2，j对应四维超混沌分系统s2，j（j表示该系统的不同变量，j=4，5，6，7）。

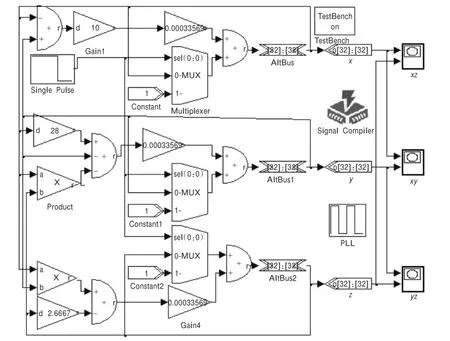
图1 DSP Builder中Lorenz混沌系统结构框图

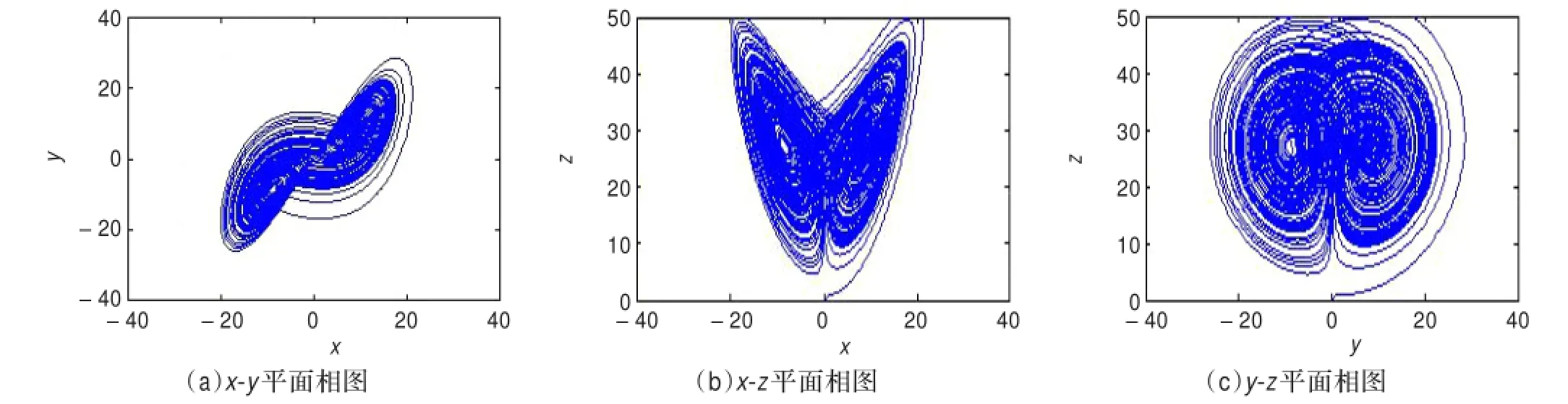
图2 离散化后的Lorenz混沌系统中的各吸引子相图

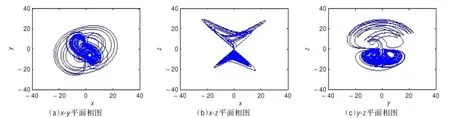
图3 离散化后的四维混沌系统各吸引子相图

因此，以这两个分系统构成的混沌分时切换系统可产生9个不同的输出，可连续地从一个分系统的任意一个变量切换到另外一个分系统的任意一个变量。根据实际需要可设置多路输出，以2路为例，系统的两路输出可产生不同变量之间的二维混沌吸引子。

4.1 硬件设计

本文中选择的FPGA是Cyclone系列，型号为EP3C25E144C8。该器件核电压为1.2 V，共有逻辑单元22 320个，用户I/O接口80个，存储位608 256个，132个9位的嵌入式乘法器，锁相环4个，全局时钟10个。采用JTAG接口或ASP接口模式下载，外接50 MHz晶振，片外接有16 Mb专用存储芯片。

单片机选择高速、低功耗和超强抗干扰的STC89LE52RC，指令代码完全兼容传统的8051单片机，12时钟/机器周期和6时钟/机器周期可以任意选择。为了实现不同混沌系统之间的切换，由单片机提供控制字，完成单片机与FPGA之间的通信。多混沌吸引子切换系统整体框图如图4所示。

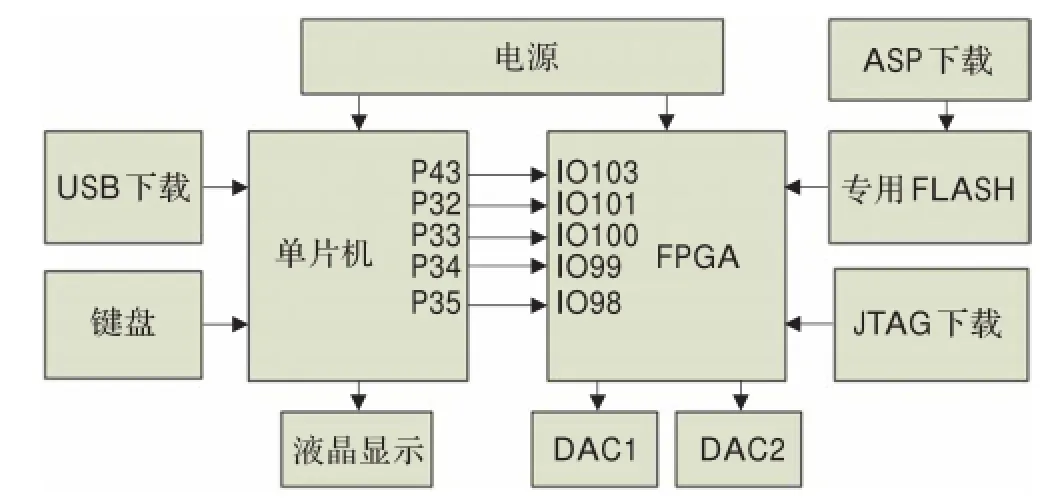
图4 多混沌吸引子切换系统框图

图4中，P34和P35是与FPGA固定相连的，其余三条则是根据需要来选择接通还是断开。FPGA利用JTAG和ASP可实现两种方式进行下载。DAC选择14位的DAC904E，两个DAC模块则分别与FPGA的14个通用IO口相连用于输出模拟的混沌吸引子。

单片机部分传递控制字是通过按键控制的。以P10～ P13作为键盘的行，以P14～P17作为键盘的列，实现键盘扫描，能够实现多混沌系统的分时切换。用PL2303芯片实现对电路的5 V供电和单片机的程序下载。将P00～P04与LCD5110液晶相连接，实现当前混沌系统信息的输出。

4.2 软件设计

用Modelsim进行功能仿真后，从得到的VHDL语言程序生成对应分混沌系统的Quartus II原理图输入模块，用于整体的Quartus II原理图输入设计。利用Quartus II软件进行原理图输入设计、分析、综合、适配和下载。通过高速数模转换芯片，就可以利用示波器观察模拟混沌信号。用Keil uVision4软件对单片机程序进行设计、编译和下载。单片机和FPGA的通信采用串行接口，接口信号线数量大幅度减少。通过键盘输入控制不同混沌系统信号的分时切换，采用液晶屏5110显示混沌系统信息。如图5所示为Quartus II中不同混沌系统之间的分时切换系统原理图输入设计。

图5中lorenz_GN模块和siwei_GN模块是分别经过DSP Builder生成的Lorenz混沌系统和四维混沌系统对应VHDL语言程序的原理图模块；shiftre模块是一个移位寄存器模块，用于串行接收单片机传送的控制字；mux21a模块为不同混沌系统之间的选择模块；CONTROL模块是用于通过判断控制字来决定输出选定混沌系统某一平面混沌吸引子相图。

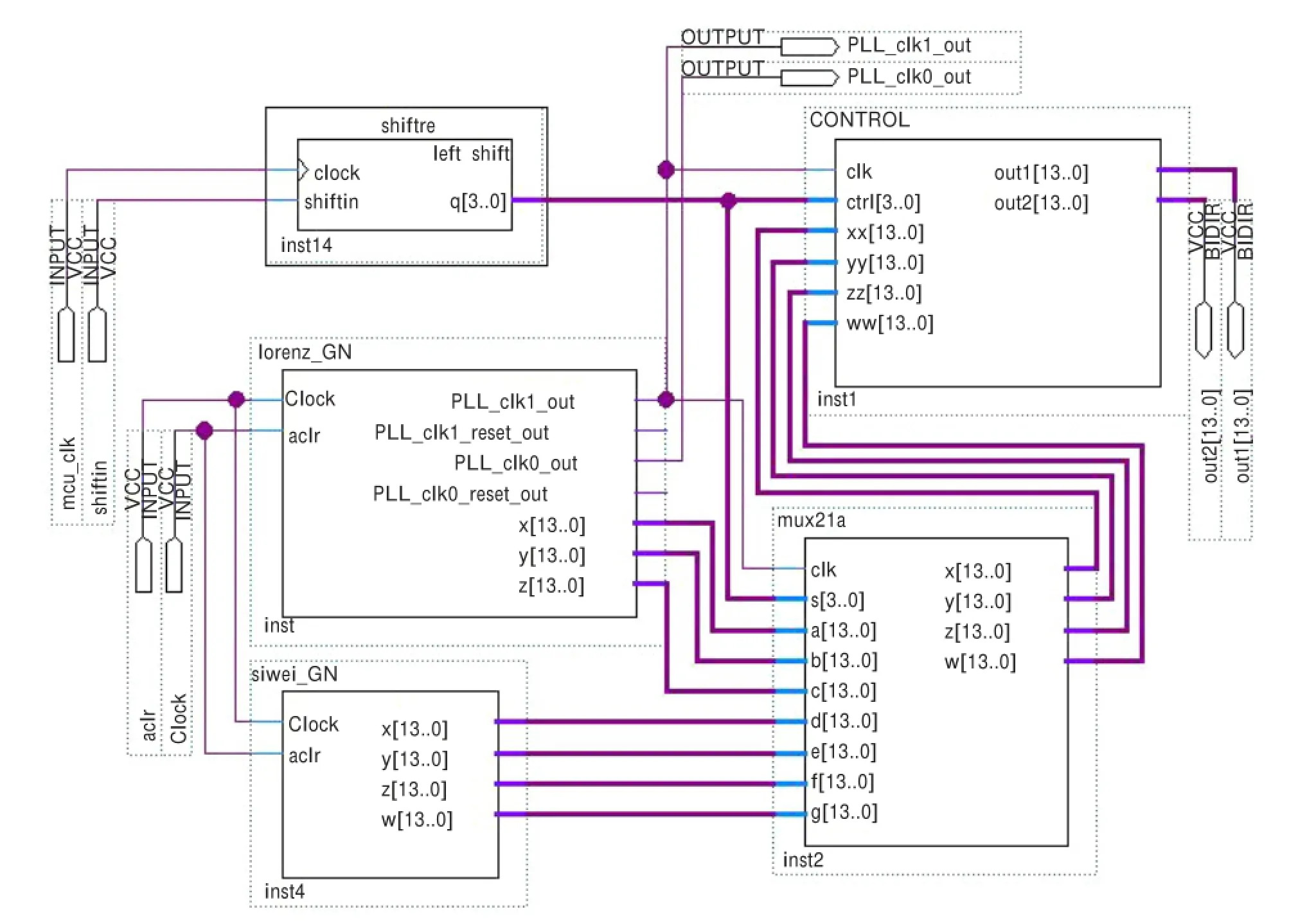
图5 不同混沌系统间分时切换的系统原理图输入设计

具体工作原理：shiftin输入端口在时钟输入mcu_clk的作用下将控制字移入移位寄存器。首先，mux21a模块根据控制字的不同选择输出某个混沌系统的吸引子相图。然后，再次输入控制字，移位寄存器将控制字传递给控制模块，由控制模块判断应该将选定混沌系统的某一平面混沌吸引子相图输出。其中PLL_clk1_out与PLL_clk0_out用于向DAC模块提供时钟。

5 实验结果与分析

如图6所示是通过单片机控制，在示波器上观察到的部分不同变量之间的二维混沌吸引子相图。

图6 示波器输出的三维、四维混沌吸引子相图

由图6可见，基于单片机和FPGA实现的多混沌吸引子切换系统产生的混沌吸引子清晰、饱满。进一步分析可知，本文设计的分时切换系统是通过单片机进行控制的，切换灵活，组合的方式变化多样。由于采用完全不同的混沌进行分时切换，在整段时间上所形成的混沌信号，相比于一个系统的改变（某个参数或变量的不同子系统之间切换）所形成的混沌信号更加复杂。因而使系统的预测重构难度增强，应用到切换混沌同步的保密通讯，可以进一步增强混沌保密通信的安全性能。

6 结论

本文的多混沌吸引子分时切换系统运用单片机技术结合FPGA技术，基于构造的多混沌分时切换表达式，通过巧妙的软件设计和简易的硬件电路，控制数字式混沌信号的产生，可以方便地在同一个混沌系统中对其相图进行分时切换，同时也可以在多个完全不同混沌系统之间进行分时快速切换。实验结果与仿真结果完全一致。事实上，本系统设计方法还可应用到其他混沌系统，可以扩展到更多混沌系统的切换。并且切换的方式也可以根据信源（欲加密信号）特点设置开关函数实现多个混沌变量的分时输出，在整个时间上获取具有时变性、多样性和复杂性特点的混沌信号，以实现信源的加密，增强加密效果和抗破译能力。

[1]刘扬正，姜长生.关联可切换超混沌系统的构建与特性分析[J].物理学报，2009，58（2）：771-778.

[2]孙友林，伍俊杰，陈君.两个超混沌系统自动切换电路的设计和仿真[J].现代电子技术，2011，34（22）：191-193.

[3]赵莉，唐文.基于Simulink的Dynamos混沌系统仿真[J].现代电子技术，2012，35（4）：7-8.

[4]周武杰，禹思敏.基于IEEE2754标准和现场可编程门阵列技术的混沌产生器设计与实现[J].物理学报，2008，57（8）：4738-4747.

[5]刘扬正，林长圣，李心朝.切换统一混沌系统族[J].物理学报，2011，60（4）：79-87.

[6]王忠林，黄娜.一个自动切换混沌系统的设计与FPGA实现[J].中国海洋大学学报：自然科学版，2010，40（4）：111-114.

[7]Wang Guangyi，Bao Xulei，Wang Zhonglin.Design and FPGA implementation of a new hyperchaotic system[J]. Chinese Physics B，2008，17（10）：3596-3602.

[8]王忠林.混沌吸引子及FPGA实现[J].计算机工程与应用，2008，44（36）：85-86.

[9]林彩霞，郝建红.基于混沌切换系统的语音加密[J].动力学与控制学报，2008，6（3）：254-259.

[10]刘扬正，姜长生，林长圣，等.四维切换超混沌系统[J].物理学报，2007，56（9）：5131-5132.

[11]杜睿山，尚福华，李阳.复合混沌映射在语音算法加密中的应用[J].计算机工程与应用，2009，45（7）：103-104.

[12]Ge Zhengming，Yang Kunwei.Chaotic ranges of a unified chaotic system and its chaos for five periodic switch cases[J].Chaos，Soliton and Fractals，2007，33（1）：246-269.

[13]刘扬正，林长圣，李心朝，等.Logistic-Unified混杂混沌系统[J].物理学报，2011，60（3）：101-106.

[14]张成亮，胡春华，王忠林.三系统自动切换混沌电路的设计与实现[J].山东大学学报：理学版，2012，547（8）：108-113.

[15]刘扬正，林长圣，王忠林.新的切换四涡卷超混沌系统及其电路实现[J].物理学报，2010，59（12）：8407-8413.

[16]王忠林，姚福安，李祥峰.基于FPGA的一个超混沌系统设计与电路实现[J].山东大学学报，2008，43（12）：93-96.

ZHANG Jianguang1,KANG Shouqiang1,JI Bin1,SONG Lixin1,ZHENG Shi2,ZHU Jianliang1

1.School of Electrical and Electronic Engineering,Harbin University of Science and Technology,Harbin 150080,China
2.Network Management Department,China Mobile Group Heilongjiang Co.,Ltd,Harbin 150028,China

In order to strengthen the encryption effects and the anti-crack ability,from the perspective of switching among multiple chaotic systems,this paper realizes a time-sharing switched system.The system can switch among multiple chaotic attractors rapidly at any time.The system uses discrete chaotic equation,defines the charts of multiple chaotic systems, combines with the DSP Builder in the MATLAB,then generates the VHDL language programs corresponding to system charts and the simulation files for Modelsim.According to the expressions of time-sharing switched systems,it improves the VHDL language programs and the programs for MCU.Eventually using the communication between MCU and FPGA, it implements a multiple chaotic attractors time-sharing switched system.By experimental verification,the system not only can achieve the switches between the same chaotic system,but also the switches between multiple chaotic systems.Thus the system can provide chaotic signals include more time-varying,diversity and complexity.

chaotic attractor;switched system;micro control unit;Field Programmable Gateway Array（FPGA）

为了增强加密效果和抗破译能力，从多个混沌系统切换的角度出发，实现了任意时刻、快速的多混沌吸引子的分时切换系统。该系统利用离散化的混沌方程，在MATLAB中结合DSP Builder构架出多混沌系统框图，继而生成系统框图对应的VHDL语言程序和用于Modelsim的仿真文件。根据构造的多混沌分时切换表达式，对VHDL语言程序进行完善及单片机程序的编写，利用单片机与FPGA的通信，实现了一种多混沌吸引子分时切换系统。通过实验验证，不仅可以实现同一混沌系统相平面之间的混沌吸引子切换，而且还可以实现多个混沌系统吸引子之间的快速分时切换。从而可为混沌加密提供更具有时变性、多样性和复杂性的混沌信号。

混沌吸引子；切换系统；微控制器；现场可编程门阵列

A

TN914

10.3778/j.issn.1002-8331.1310-0269

ZHANG Jianguang,KANG Shouqiang,JI Bin,et al.Implementation of chaotic attractors switched systems by using MCU and FPGA.Computer Engineering and Applications,2014,50（18）：70-74.

哈尔滨市科技创新人才专项基金（留学回国人员）（No.2013RFLXJ019）。

张建广（1990—），男，硕士研究生，研究领域为混沌信号产生与应用；康守强（1980—），通讯作者，男，博士，副教授，硕士生导师，研究领域为混沌信号产生与应用，振动信号处理与设备可靠性评估。E-mail：kangshouqiang@163.com

2013-10-22

2013-12-10

1002-8331（2014）18-0070-05