基于非合作博弈的改进型认知无线电功控算法
2014-07-19陈军肖明波
陈军,肖明波
杭州电子科技大学通信工程学院,杭州 310018
基于非合作博弈的改进型认知无线电功控算法
陈军,肖明波
杭州电子科技大学通信工程学院,杭州 310018
1 引言
当今,随着无线通信技术的快速发展,频谱资源的使用变得越来越紧张。一方面是由于无线频谱资源的稀缺,另一方面是由于现有的固定频谱分配方式导致无线频谱资源未能得到充分而高效的利用。为此,人们提出了一种新兴的无线智能技术——认知无线电(CR)技术[1-2]。
CR技术能够使认知用户(非授权用户)与主用户(授权用户)共享一段频谱带宽,从而实现对空闲频带的再次利用,提高频谱资源的利用率。一个基本的认知循环要经历三个过程[3]:(1)无线传输场景分析;(2)信道状态估计及其容量预测;(3)功率控制和频谱管理。其中CR功率控制的最终目标是确保认知用户在有效地共享主用户频谱资源时,其累积干扰不会对主用户造成有害影响。
作为数学应用的一个分支,博弈论主要是研究决策主体在给定的信息结构下,如何决策以最大化自己的效用,以及不同决策主体之间如何达到均衡的问题。近年来,博弈论被广泛应用到经济、计算机和通信等领域中。由于它在处理分布式最优化问题等方面具有一定的优势,所以它在解决功率控制问题上也受到众多学者的青睐。文献[4]提出了一种基于SINR平衡的分布式算法,它虽然能够保证用户服务质量,但其收敛SINR固定,造成系统资源的浪费,使系统的吞吐量下降。文献[5]提出了一个Koskie-Gajic算法,该算法能够通过降低SINR来降低用户的发射功率,但无法保证用户的目标信干噪比。David-Goodman等人首先将博弈论应用到CDMA无线网络功率控制中[6],提出了一个非合作功率控制博弈模型(NPG),并证明了其纳什均衡的存在。因为此均衡解并不一定最优;他们又提出了一种基于代价的非合作功率控制博弈模型(NPGP)[7],用户的收益得到帕累托改善,但在一定程度上会影响用户间的公平性。
基于此模型,后来的许多学者提出了许多针对认知无线电的功率控制算法。注意,与传统的CDMA网络不同的,认知无线电网络是一个干扰温度受限的网络,CR的功率控制问题不仅仅要考虑认知用户效用收益的问题,且还需考虑认知用户对主用户累积的干扰问题和认知用户信干噪比(SINR)的最小需求问题。文献[8]提出的算法没有考虑认知用户的SINR需求,也忽略了对主用户的保护。文献[9]的算法只考虑了认知用户对主用户的累积干扰,忽略了认知用户的SINR需求。文献[10-11]的算法虽然考虑到了认知用户的SINR需求,但没有讨论对主用户的保护问题。
本文根据CR系统中不同类型用户服务质量(QoS)要求的特点,提出了一种改进的非合作功率控制博弈算法,该算法不仅考虑了认知用户最小SINR需求、认知用户间的干扰及主用户对认知用户的干扰,同时还考虑了认知用户对主用户产生的累积干扰。
2 系统模型
研究一个与3G蜂窝网络共存的复合型CR网络系统模型,如图1所示。其中,M个主用户(PU)使用授权频段和3G蜂窝网的一个主基站(BSp)进行通信;一个没有授权频谱的单蜂窝认知网络系统位于3G蜂窝网内,N个认知用户(CU)以“衬底”的方式与PU共享频谱资源,并使用CDMA体制把数据传送到次级基站(BSs)。
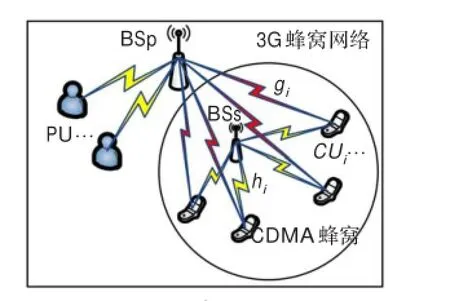
图1 系统模型
考虑上行链路的方案,设第i个认知用户(CUi)的发射功率为pi,到BSs的链路增益为hi(i=1,2,…,N),则CUi在BSs处的接收功率为pihi;CUi到BSp的链路增益为gi。di和Di分别是CUi到BSs和BSp的距离。则CUi在BSs处的接收信干噪比(SINR)为:


设表示CUi的SINR阈值,一旦系统允许其发送信息,就要保证其在BSs处的SINR大于目标SINR阈值:

这个约束条件对CR网络而言是十分必要的。因为如果CU服务质量得不到保证,那么CU发送信号不仅会浪费能量,还会对PU及其他CU造成不必要的干扰。另外,为了使CU在与PU共享频谱带宽时不对PU造成有害干扰,各CU发射功率还应满足下式:


3 基于非合作博弈的功率控制
3.1 功率控制博弈模型的定义
在认知无线电中,一个完整的博弈模型包括三个基本要素:(1)参与者,他们是参与博弈的决策主体方,在整个博弈的过程中以最大化自己的利益为目标;(2)策略空间,参与者可选择的所有策略组成的空间集合;(3)收益函数,参与者最关心的实际利益,通常用效用函数Ui(pi,P-i)来表示,即当CUi的发射功率为pi,其他CU选择的功率为P-i时,CUi所获得的效用。
博弈的最终目标是找到一个最佳的策略组合,使每个参与者的策略都是对其他参与者策略的最优反应,即达到纳什均衡NE。结合式(3)和式(5)的约束条件,并考虑到认知用户的发射功率是受限的,CR网络系统中CUi与PU共享频谱带宽时的功率控制博弈问题可定义为,对于i∈N:


3.2 效用函数和代价函数的设计
3.2.1 效用函数的设计
考虑到效用函数需满足非负性、凸性且存在极值的要求,本文采用了以下反正切函数来作为CUi的效用函数,其表达式为:
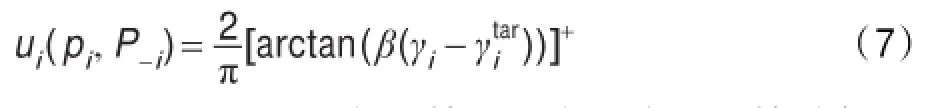
其中[X]+=max(X,0),常系数2/π是对效用函数进行的归一化处理,β是效用函数的陡峭系数,可用来实现CU在发射功率和SINR之间的折中。当β较小时,曲线坡度较平坦,较大的SINR才能满足CU的QoS需求;反之,当β较大时,曲线坡度较陡,CU的SINR只需稍微大于目标SINR,其QoS就能够得到满足。应该指出,虽然这里选择了反正切函数来作为本文的效用函数,但本文算法也适用于其他类似的效用函数[12]。
3.2.2 代价函数的设计
在NPG模型中,在用户发射功率不变的情况下,无论哪个CU单独增加其发射功率都会使其他CU的效用降低;效用降低的CU也通过增加自己的发射功率来提高自己的效用,最终每个CU的均衡功率都将增大,这样一来对PU的干扰也将随之增大,可能影响PU的正常工作。为了解决这个问题,文献[7]引入了用户发射功率的线性函数作为其代价函数。这在一定程度上使每个CU的收益得到帕累托改善,但却失去了频谱共享的公平性。为了改善认知系统的公平性,本文在代价函数中引入链路状态信息,根据CU的链路质量调节其代价大小;同时还根据认知用户发送消息时对PU造成干扰的程度,来调节其代价大小。基于以上分析,本文引入了如下的代价函数:

3.3 IPC-NG算法的设计
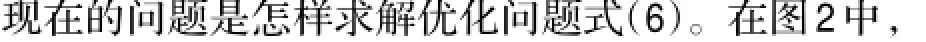


图2 认知用户i的效用和代价函数图

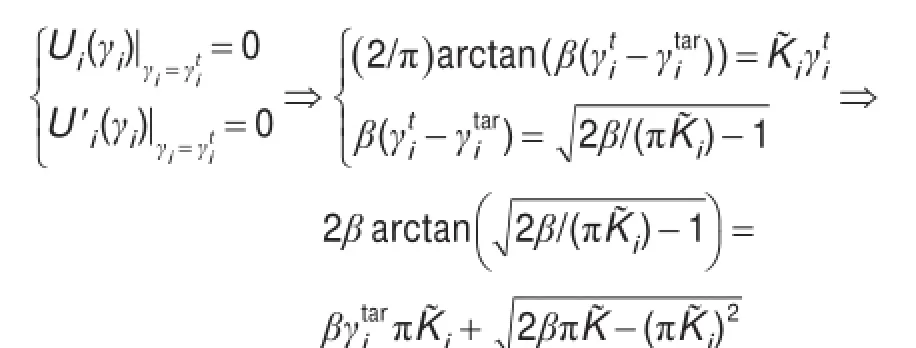
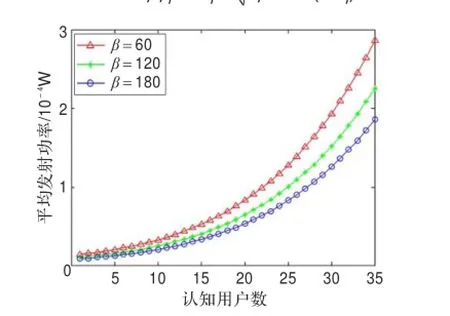
图3 陡峭系数对平均发射功率的影响

3.4 IPC-NG算法纳什均衡的存在性和收敛性
定义1如果Ui(pi,P-i)≥Ui(p′i,P-i),∀i∈N,pi∈Pi,则功率矢量P=(p1,p2,…,pN)为非合作功率控制博弈G={N,A,ui(p)}的纳什均衡。
定理1IPC-NG算法存在纳什均衡。
证明根据纳什均衡的不动点原理[13],要证明该算法存在纳什均衡,只需证明算法满足以下两个条件:(1)CU的发射功率集合是欧几里德空间RN上非空的、闭的、且有界的凸集;(2)Ui(pi,P-i)在功率集合上是连续的、拟凹的。显然,该算法是满足第一个条件的,且Ui(·)在pi上是连续的,下面只需证明Ui(·)在pi上是拟凹的。由于式(10)右边第二项与pi无关,故易知:

将认知系统中各认知用户的功率记为P=[P1,P2,…,PN]T,根据文献[15]有:
引理1如果P≥0,使用功率控制算法P(k+1)=R(P(k))后,系统收敛的充要条件是:
(1)正定性,即R(P)≥0;
(2)单调性,如果P′≥P,则R(P′)≥R(P);
(3)可扩展性,∀ξ>1,有ξR(P)>R(ξP)。
对于任何的功率控制算法,当应用到一个实际系统中时,如果满足以上引理的三个条件,就能够证明无论是在同步还是在异步的情况下,都可以收敛到唯一的固定点。
定理2IPC-NG算法是收敛的。
证明因为pi∈[0,pi,max],同时pi=γiIi/Ghi是关于发射功率的单调递增函数,所以R(P)满足引理1的前两个条件(即正定性和单调性)。至于可扩展性,∀ξ>1,有:
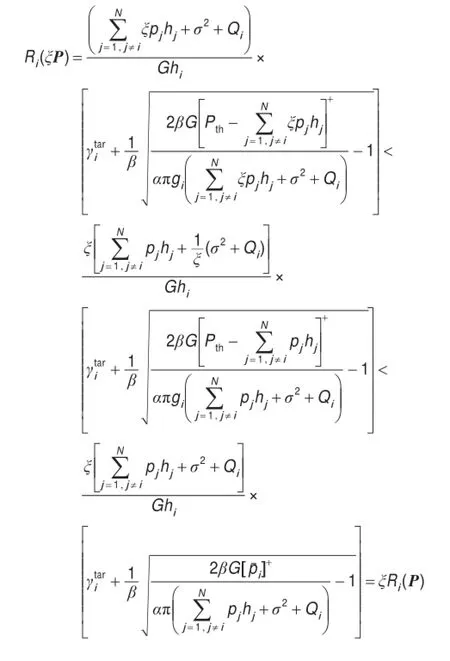
故IPC-NG算法满足引理1的三个条件。证毕。
4 仿真结果及性能分析
本章用数值仿真的方法来评估提出算法的性能。仿真参数的设置如下:认知用户数N=[1,35],主用户数M=2,认知用户到BSs的距离区间d=[320,1 000],认知用户到BSp的距离区间D=[200,1 050],数据传输速率R=1×104bit/s,频谱带宽W=5×106bit/s,干扰温度门限Pth=1.5×10-14W,背景噪声功率为σ2=5×10-15W,目标信干噪比γtiar=5。忽略快衰落及阴影效应的影响,使用的信道增益模型为:,其中ζ为衰减因子,通常取2~6,A为常数增益,在本仿真中分别取为3.6和0.007 5。另外为简单起见,将主用户j对认知用户i的干扰定义为主用户j到认知网络次级基站距离的函数,即Qi=θH-0.3,其中H=700,900,为主用户到次级基站的距离,θ为常数。
首先,仿真了在不同β的情况下,随着认知用户数的增加,认知用户平均发射功率和平均SINR的变化图。然后,仿真了在不同α的情况下认知用户平均发射功率和平均SINR的变化图。其次,验证了IPC-NG算法的收敛性及收敛速度。再次,在平均发射功率、SINR两方面,对IPC-NG算法、冯-罗(Feng-Luo)算法、SINR平衡算法、Koskie-Gajic算法进行了对比分析;最后,在系统吞吐量方面对它们进行了对比分析;另外又对IPC-NG算法、Feng-Luo算法、NPGCsigmoid算法[3]和NPGCJsyn算法[16]的净效用进行了对比分析。
由图3、4可知,随着β的减小,认知用户的平均发射功率增加,平均SINR增大。因为β越大,效用函数曲线坡度越陡,认知用户只需较小的发射功率,使认知用户的SINR稍微大于目标SINR,其QoS就能够得到满足;相反,β越小,认知用户SINR要求较高,于是以增大发射功率来换取SINR的提高。所以,β可用来实现认知用户在发射功率和SINR之间的折中。

图4 陡峭系数对平均SINR的影响
由图5、6可知,当代价系数增大时,认知用户平均发射功率降低,平均SINR减小,即认知用户以牺牲少量的SINR为代价,换来发射功率的降低,而发射功率的降低能使认知用户的电池寿命延长,同时也减少认知用户对主用户及其他认知用户的干扰。
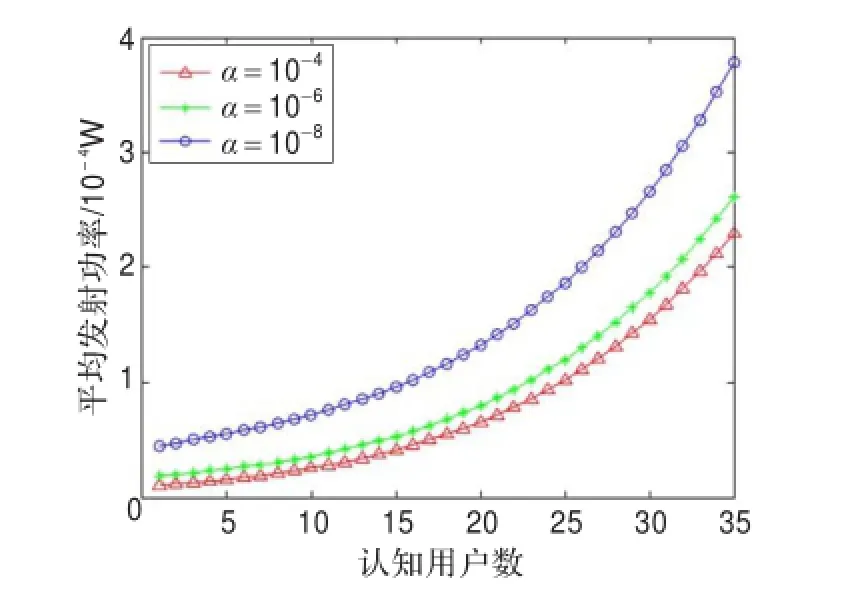
图5 代价系数对平均发射功率的影响
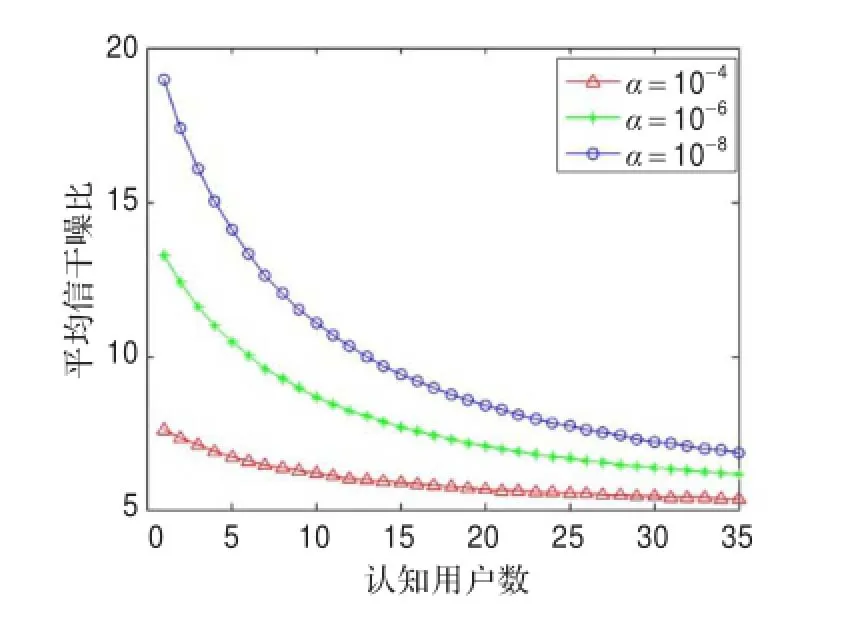
图6 代价系数对平均SINR的影响
为简单起见,对5个固定认知用户的收敛速度进行了仿真分析,图7给出了这5个认知用户发射功率经过45次功率迭代后得到的结果。由图可知,利用IPC-NG算法,经过7次功率迭代后各认知用户的发射功率趋于一个稳定的常数值,所以本文算法收敛速度快且具有较好的收敛性。

图7 认知用户发射功率迭代过程
从图8、图9可以看出,与SINR平衡算法、Koskie-Gajic算法相比,IPC-NG算法可牺牲较小的发射功率,换来较高的认知用户QoS改善(以SINR度量);而与Feng-Luo算法相比,IPC-NG算法在认知用户发射功率和QoS方面都得到了较大的改善。由图9可知,在小区容量范围内,SINR平衡算法的信干噪比一直保持在目标值上,虽然这有利于系统的公平性,却会使系统资源的利用率下降,造成资源浪费;而Koskie-Gajic算法过分强调对认知用户发射功率的控制而忽视认知用户本身的QoS需求,无法保证认知用户的SINR,不适用于对服务质量要求比较严格的系统;虽然IPC-NG算法的SINR随着认知用户数的增加有所减少,但都能保证认知用户的QoS要求。
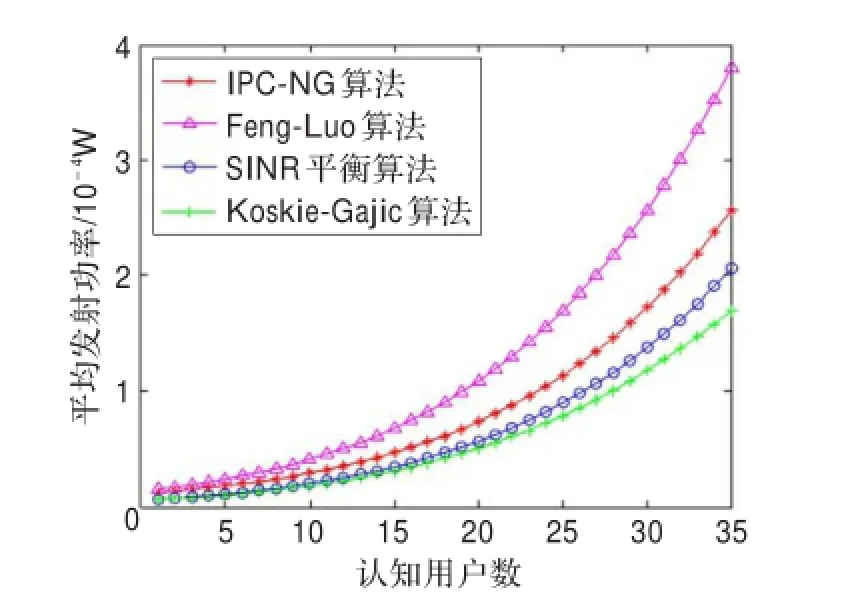
图8 平均发射功率比较
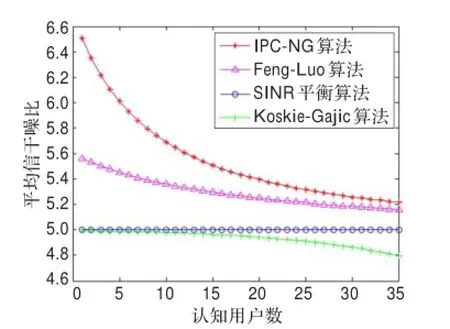
图9 平均SINR比较
由图9、图10可知,IPC-NG算法不仅考虑到了每个CU的QoS需求,同时也兼顾了认知系统的吞吐量,且可以通过调整系统参数来控制认知用户的发射功率,从而降低认知用户间的干扰,提高认知系统的性能。

图10 吞吐量的比较
图11对比仿真分析了由IPC-NG算法、Feng-Luo算法、NPGCsigmoid算法和NPGCJsyn算法得到的分布在次级基站周围的7个不同认知用户的均衡效用。由图可知,与其他3个算法相比,IPC-NG算法对认知用户均衡效用的提高最为明显。随着认知用户与次级基站间的距离逐渐增大,4个算法得到的认知用户的均衡效用不断减少,且由它们得到的均衡效用的差距也逐渐减小,但IPC-NG算法相比于另外3个算法的均衡效用仍具有很大的优势。
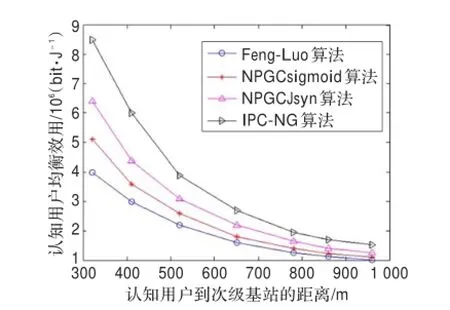
图11 净效用比较
5 结论
本文根据认知无线电网络的特点,在原来NPG模型的基础上引入了新的效用函数和代价函数,提出了一种改进的非合作博弈认知无线电功率控制算法,此算法将认知用户和主用户区别开来,在认知用户与主用户共享频谱带宽时,既考虑了认知用户的最小信干噪比需求,又考虑到了认知用户对主用户产生的累积干扰。最后的仿真结果表明,本文所提出的改进算法不仅可以避免对主用户产生有害影响,同时还保证了每个认知用户的QoS需求,提高了认知系统的吞吐量和净效用。本文仅考虑了单信道单小区的3G蜂窝系统,下一步工作是将此算法推广到多信道多蜂窝的认知无线电系统和Ad Hoc网络中。
[1]Mitola J.Cognitive radio:making software radios more personal[J].IEEE Personal Communication,1999,6(4):13-18.
[2]Jondral F K.Cognitive radio:a communications engineering view[J].IEEE Wireless Communications,2007,14(4):28-33.
[3]王霞,朱琦.一种改进的认知无线电博弈功控算法[J].信号处理,2009,25(5):825-831.
[4]Foschini G J,Miljanic Z.A simple distributed autonomous power control algorithm and its convergence[J].IEEE Transactions on Vehicular Technology,1993,42(4):641-646.
[5]Koskie S,Gajic Z.A nash game algorithm for SINR-based power control in 3G wireless CDMA networks[J].IEEE/ ACM Transactions on Networking,2005,13(5):1017-1026.
[6]Goodman D,Mandayam N.Power control for wireless data[J].IEEE Personal Communication,2000,7(2):48-54.
[7]Saraydar C,MandayamNB,Goodman DJ.Efficient power control via pricing in wireless data networks[J]. IEEE Trans on Communication,2002,50(2):291-303.
[8]Liu Lixia.Power control algorithm based on new-style utility function in cognitive system[C]//Computer Application and System Modeling(ICCASM),2010.
[9]Wu Shuang,Xu Wang,Liu Jian.A power control game via new pricing with dynamic coefficient in cognitive radio[C]// Communications and Mobile Computing(CMC),2011.
[10]Cheng Shilun,Zhen Yang.Energy-efficient power control gameforcognitiveradiosystems[J].IEEEComputer Society,2007,1(30):526-530.
[11]冯冀,罗新民,罗俊平.认知无线电中基于非合作博弈的功率控制算法[J].电子技术应用,2008(4):110-114.
[12]Xiao M,Shroff N B,Chong E K P.A utility-based power control scheme in wireless cellular systems[J].IEEE/ACM Transactions on Networking,2003,11(2):210-221.
[13]Fienberg D,Tirol J.Game theory[M].Cambridge,MA:MIT Press,1991:23-26.
[14]Roberts A W,Varberg D E.Convex functions[M].New York:Academic Press,1973.
[15]Yates R D.A framework for uplink power control in cellular radio systems[J].IEEE Journal on Selected Areas in Communications,1995,13(7):1341-1347.
[16]康钰,朱琦,酆广增.认知无线电系统中一种改进的功率控制博弈算法[J].电路与系统学报,2010,15(2).
CHEN Jun,XIAO Mingbo
School of Communication Engineering,Hangzhou Dianzi University,Hangzhou 310018,China
In cognitive radio network,where Cognitive Users(CUs)share spectrum bandwidth with the Primary Users(PUs),it is necessary for cognitive users to perform power control to guarantee their QoS and avoid affecting PUs.In this paper,an improved power control algorithm based on non-cooperative game(IPC-NG)is proposed,with cost functions based on link gains and interference temperature.It is proved that the Nash equilibrium exists uniquely for the new net utility function through mathematical derivation and theoretical analyses.In the meantime,the convergence rate of the algorithm is analysed.Simulation results show that the algorithm not only avoids the influence for PU and guarantees the QoS of CUs,but also increases the system throughput and net utility.
cognitive radio;non-cooperative game;power control;utility function;price function
在认知无线电网络中,当认知用户(CU)与主用户(PU)共享频谱带宽时,需要对认知用户的发射功率进行控制,以确保认知用户在满足自己的QoS且不影响主用户的前提下与主用户共享频谱带宽。利用博弈论的方法,设计了一种基于链路增益和干扰温度的代价函数,并据此提出了一种改进型非合作博弈功率控制算法(IPC-NG)。通过数学理论推导分析,证明了新的净效用函数存在纳什均衡且均衡点唯一,同时还分析了该算法的收敛速度。仿真结果表明,该算法不仅避免了对主用户的影响,也保证了每个CU的QoS需求,同时还提高了认知系统的吞吐量和净效用。
认知无线电;非合作博弈论;功率控制;效用函数;代价函数
A
TN914.53
10.3778/j.issn.1002-8331.1210-0194
CHEN Jun,XIAO Mingbo.Improved power control algorithm based on non-cooperative game in cognitive radio. Computer Engineering and Applications,2014,50(18):220-225.
国家自然科学基金(No.30900328);杭州电子科技大学启动基金项目(No.KYS085612006)。
陈军(1986—),男,在读研究生,主要研究方向:认知无线电资源分配;肖明波(1971—),男,教授,博士生导师,主要研究方向:无线通信网络、数字版权保护、数据挖掘与融合等。E-mail:junchen6@126.com
2012-10-18
2012-12-04
1002-8331(2014)18-0220-06
CNKI网络优先出版:2013-01-11,http://www.cnki.net/kcms/detail/11.2127.TP.20130111.0953.016.html
