房地产价格波动集聚性和杠杆效应的实证研究＊

王 敏，杨黎明，余 劲

（西北农林科技大学 经济管理学院，陕西 杨凌712100）

金融资产的波动一直是经济研究人员和投资者关注的焦点。在金融资产市场上，由于投资者心理预期和信息的不对称等因素影响，资产价格的波动常常表现为非均衡状态，主要特征为分布呈尖峰厚尾性、波动时变性和聚集性、长期记忆性、波动溢出效应以及杠杆效应。波动聚集性指随机扰动项在一定的时间内波动幅度较大，而在一定的时间内波动幅度较小，波动具有正的相关性。这在金融资产价格波动中表现为，较大幅度的波动后面伴随着较大幅度的波动，而在较小的波动后面紧接着较小幅度的波动。波动聚集性出现的原因一般认为有两种解释：第一种解释认为该现象源于外部冲击对价格波动的持续性影响，在市场有效的情况下，高频数据表现的ARCH效应就是信息以集聚方式到达的反映；第二种解释就是Stock所提出的时间扭曲观，即波动聚集性的产生是因为经济事件的发生时间与日历时间不一致。资本市场的冲击是非对称的，利空消息和利好消息对资产价格波动会产生不同的影响，这种非对称性允许波动率对市场下跌的反应比对市场上升的反应更加迅速，即存在“杠杆效应”。一般而言，在资产市场上，投资者对负的价格变化比对正的价格变化更加敏感，资产的向下运动通常伴随着比之程度更强的向上运动。作为重要的金融资产，房地产市场也具有金融资产的各种特征。近几年全国各个地区房价大幅度上涨，虽然政府出台了许多调控措施，中央银行也频繁动用货币政策手段，但成效始终不大，其中一个重要的原因在于对房地产价格尤其是一线和二线城市的房地产价格波动的集聚性和杠杆效应缺乏正确的判断，对于利空消息和利好消息将对房地产价格产生的影响没有作出合理的预测。基于此，本文拟采用2001年第一季度至2012年第三季度的相关数据，通过构建TARCH模型，分析我国一线和二线城市房地产价格的波动集聚性和杠杆效应①。

一、文献综述

由于房地产市场非常庞杂，具有强烈的地域性，交易也不如股票那样频繁，而且具有投资和消费的双重属性，因此房地产价格波动集聚性和杠杆效应的分析并不多见，目前相关研究主要是集中在欧美等发达国家。Dolde等［1］利用GARCH模型研究了房地产价格的波动，发现美国旧金山的房地产市场存在波动时变性；Guirguis等［2］的研究则发现西班牙的房地产投资收益具有波动聚集性；Szu－Yin Kathy Hung等［3］利用 GARCH 均值模型检验了房地产投资信托的动量收益的波动性，发现动量收益具有不对称波动；Kim Hiang Liow等［4］利用GARCH协整模型研究了亚太地区房地产市场的波动聚集性；Miles［5］的研究表明，美国超过一半以上的州的房地产价格增长率具有波动集聚性，而且房地产价格波动存在非对称效应。

国内对房地产价格波动的研究多采用向量自回归模型，侧重于探讨影响房地产价格波动的各个因素，例如吴燕华等［6］建立VAR模型研究了货币供应量和利率变化冲击对房地产价格的动态影响；刘轶等［7］运用VAR模型对北京、上海、广州和深圳的房地产价格和热钱流入量进行了实证检验，发现两者之间存在长期均衡关系；时鹏等［8］利用VAR模型对陕西房价、地价和M2进行了检验；车欣薇等［9］对香港、北京、上海和深圳四个金融中心城市与银行信贷进行实证分析，发现各金融中心城市房地产价格与银行信贷间存在长期的均衡关系。国内对房地产价格波动的聚集性和杠杆效应的关注和分析是从最近几年开始的，如刘洪玉等［10］研究了房价波动过程，结果显示，北京、广州和深圳的房价具有较显著的波动群聚特征，但TARCH等模型的特征不显著；徐轲等［11］对中国住房均价及四大直辖市数据进行实证研究，结果表明，无论长期还是短期我国的房地产价格均存在波动集聚性，除重庆外的其他3个直辖市也存在集聚性；孟卫东等［12］对沪深地产指数收益率的波动进行了估计，结果表明沪深地产指数收益率的波动不存在杠杆效应，投资者投机目的较强。

在研究价格波动方面，ARCH类模型无论从理论研究的深度还是从实证运用的广泛性来说都是独一无二的。该模型在金融资产研究领域的应用非常广泛，尤其是在股票领域。如Tae Hyup Roh［13］对股票价格指数的波动进行预测表明，混合的NN－EGARCH模型能够产生杠杆效应；Yue Xu等［14］通过GARCH模型分析后认为，中国金融日收益具有显著的集聚性，并检验了上海股票市场的杠杆效应；Xing Jingli［15］利用 ARIMAEARCH－M（1，1）和 ARIMA－TARCH－M（1，1）模型对我国股票市场的波动性进行研究发现，上海和深圳的股票市场价格具有波动聚集性、非对称性以及尖峰厚尾的特征；陈浪南等［16］分析了利好消息和利空消息对股票市场的非对称影响，发现中国股票市场在10%显著水平上存在杠杆效应；李卢霞［17］认为中国股市存在着明显的杠杆效应，并表现出较明显的向均值复归的特征。

研究表明，ARCH类模型在国内外股票市场的相关研究中的应用已比较成熟，在研究金融资产波动方面具有无可比拟的优势，然而目前国内研究的侧重点仍然更多地关注各因素对房地产市场的冲击程度，对各个区域房地产价格波动的集聚性和杠杆效应的研究才刚刚起步；同时，应用ARCH类模型对房地产价格波动的分析主要集中在波动集聚性上，对其波动的杠杆效应分析较为缺乏；此外，在房地产价格的波动集聚性分析中，现有文献也大都侧重于分析全国和北京、广州、深圳这几个大城市的房价波动上，对于70个大中城市房地产价格波动集聚性的分析也基本上处于空白，也偏离了目前我国房地产价格波动监测集中在70个大中城市的事实。据此，本文将采用TARCH模型，将其应用到我国一线和二线城市房地产价格波动的研究中，分析房地产价格波动集聚性和杠杆效应。

二、模型构建与变量选择

（一）模型构建

自回归条件异方差模型（autoregressive conditional heteroskedasticity model，ARCH 模型）最早由恩格尔在1982年提出。ARCH类模型赋予条件方差以自回归结构，集中反映方差变化特点，允许波动的冲击持续各期。这种持续性能够反映金融资产收益中比较明显的变化是否具有规律性，并且说明这种变化前后依存的内在传导是否来自某一特定类型的非线性结构，较好地解释了在外部冲击下资产收益的聚集倾向，因而适用于大量文献涉及的资产收益的非正态性和不稳定性分布。这也使得该模型广泛应用于经济学各个领域，尤其是用在金融时间序列分析中。作为ARCH族模型中的一员，TARCH模型在条件方差中加入了名义变量，能够区分利空消息和利好消息对波动的影响，能够较好地验证杠杆效应的存在，因此，本文在ARCH模型的基础上构建了TARCH模型，以分析房地产价格在波动过程中的集聚性和杠杆效应。

1．基本模型。ARCH模型的主要思想是：扰动项μt的条件方差依赖于它的前期值μt－1的大小，考虑k变量回归模型：

如果μt的均值为零，对yt取基于（t－1）时刻的信息的期望，即Et－1（yt），有如下的关系：

由于yt的均值近似等于式（1）的估计值，所以式（2）也称为均值方程。

假设在时刻 （t－1）所有信息已知的条件下，扰动项μt的条件分布是：

也就是，μt服从以0为均值，（α0＋α1μt2－1）为方差的条件正态分布。

式（3）中的μt的方差依赖于前期的平方扰动项，称之为 ARCH（1）过程：由此，上述式（1）和式（3）构成了一个ARCH（P）过程。

由于ARCH模型在运用中常常会产生变量多重共线性等问题，为此，Bollerslev把ARCH模型扩展为广义ARCH模型，即GARCH模型，滞后结构更加灵活。在这个模型中要考虑两个不同的设定：一个是条件均值，另一个是条件方差。标准的GARCH（p，q）模型公式如下：

其中，方程（4）为条件均值方程，反映了序列yt的产生过程，方程（5）对条件方差σ2t的取值作出了约束，σ2t的大小取决于ε和σ2的历史值，因此该方程也被称为条件方差方程。ARCH模型和GARCH模型只能反映金融时间序列的尖峰厚尾和波动聚集现象，不能反映非对称性。

2．TARCH模型。在ARCH类模型中，常用的检验非对称信息的模型主要有两种：TARCH和EGARCH模型。EGARCH模型主要强调非对称的杠杆影响是指数的而非二次的，而本文的目的在于探讨一线和二线城市房地产价格波动中是否存在杠杆效应及杠杆效应的影响程度，因此，为了实证结果的可比性，本文拟选用门限ARCH模型，即TARCH（Threshold ARCH）模型。TARCH模型由Zakoïan等提出的，该模型是在扩展的ARCH模型的基础上加上非对称因素，其条件方差为：

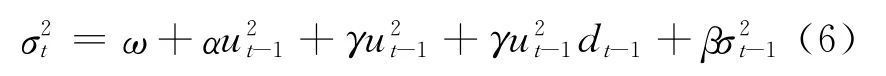
式中：dt－1为虚拟变量。当ut－1＜0时，dt－1＝1；否则，dt－1＝0，只要γ≠0，就存在非对称效应。

在式（6）中，条件方差方程中的γu2t－1dt－1项为非对称效应项，或者TARCH项。条件方差方程表明，σ2t依赖于前期的残差平方μ2t－1和条件方差σ2t－1的大小。好消息（ut＞0）和坏消息（ut＜0）对条件方差有不同的影响：好消息有一个σ的冲击，即ut－1＞0时，dt－1＝0，式（6）中的非对称项不存在，所以好消息只有一个α倍的冲击；而坏消息则有一个（α＋γ）倍的冲击，这是因为当ut－1＜0时，dt－1＝1，式（6）中的非对称效应出现，所以坏消息会带来一个（α＋γ）倍的冲击。如果γ≠0，则信息是非对称的，如果γ＞0，说明存在杠杆效应，非对称效应的主要效果是使得波动加大；如果γ＜0，则非对称效应的作用是使得波动减小。

（二）变量选择及ARCH效应检验

本文选取了2001年第一季度至2012年第三季度房地产价格的相关数据分析利好和利空消息对一线、二线城市房地产价格波动的影响。相关样本数据主要来源于中国人民银行、中国经济景气月报、国家统计局等。在模型中，利率用ir来表示，住宅销售价格指数用hp来表示。在分析中，我们依据房地产市场的特征，将70个大中城市划分为一、二、三线城市，一线城市有北京、上海、广州和深圳四个城市，二线城市随机抽取了青岛、长沙、大连、郑州、成都和西安六个城市。

在进行分析之前，对原始数据进行了处理。本文利用Census X12季节调整法对房地产价格指数进行了季节调整，以消除其中的季节因素。然后，本文通过利用ADF单位根检验以及AIC和SC准则，确定各个模型变量在滞后一阶时是平稳的，因此，在后面的模型分析中采用一阶滞后。最后，本文采用拉格朗日乘数（LM）检验法对残差进行ARCH效应的LM检验，得到了在滞后阶数p＝1时的ARCH LM检验结果，见表1。

表1 ARCH效应LM检验结果

由表1中的结果来看，无论是一线城市还是所选取的二线城市，其P值均在5%的显著性水平上拒绝原假设，说明模型的残差序列存在ARCH效应。

三、集聚性和杠杆效应的结果分析

（一）一线城市房地产价格波动的集聚性和杠杆效应

自2001年以来，北京、上海、广州、深圳四个一线城市房地产价格一直以较高幅度上涨，屡屡传出房地产泡沫崩盘或房市失控的消息，同时，这也一直是房地产开发商、投机者等进行投资和开发的首选地，从而一线城市成为政府调控房地产市场的重中之重。为了分析在利空和利好消息冲击下一线城市房地产价格波动集聚性和杠杆效应，本文构建了一线城市房地产价格波动的TARCH模型，通过模型分析，得出如下结果，见表2。

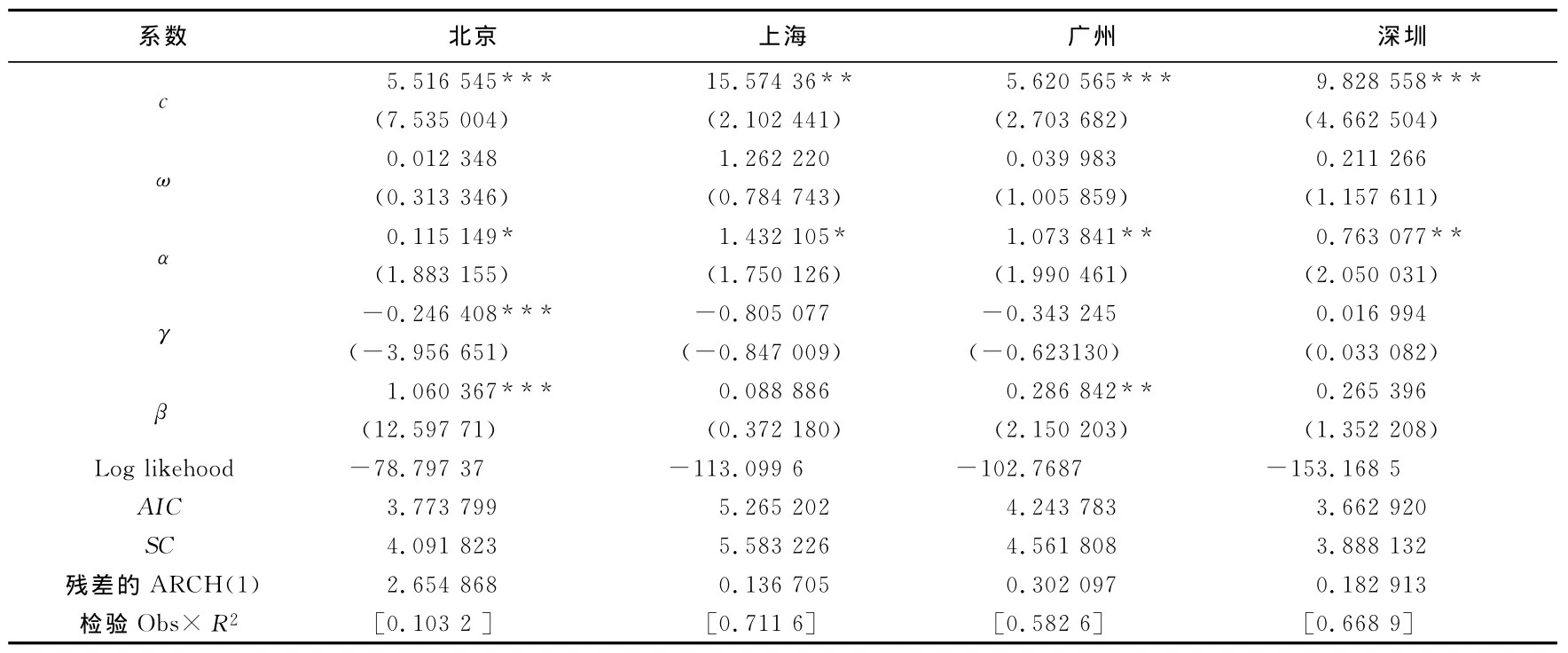
表2 一线城市房地产价格波动的TARCH模型结果

波动集聚性产生的原因有两种解释，一种是将波动与宏观经济形势联系在一起，认为信息产生过程的序列相关性导致了波动的集簇性，如果消息集中到达，那么收益就可能显示出聚集性。Bolleslev等［18］把名义利率、股票红利分配、货币供给、石油价格、商业周期和信息模式等作为波动聚集的根源；另一种是认为如果市场交易主体偏好不同，并且需要花费时间来消化信息冲击（information shock），从而消除预期差异，那么市场的动态变化趋向于波动聚集［19］。根据表2的结果可知，四个一线城市中，北京和上海的α项在10%的水平上显著，广州和深圳的α项均在5%的水平上显著，这说明一线城市的房地产价格波动表现出较强烈的ARCH效应，具有显著的波动集聚性。这可能的解释是四个一线城市最近十年里在经济快速发展的同时房价的上涨幅度随之增加，同时，在这两个城市中对房地产的需求更多地表现为投资需求，需求弹性较大，房地产泡沫较之其他地区更为严重，此外，北京、上海、深圳和广州作为中国最为重要的金融中心，对整个宏观经济的稳定具有非常重要的作用，因而是政府进行宏观调控的重点区域，这些都导致了一线城市的房地产价格波动表现出了显著的波动集聚性。

针对γ的分析可知，在四个一线城市中上海、广州和深圳的γ项在1%、5%以及10%的水平上都不显著，表明这三个城市的房地产价格波动没有显示出强烈的TARCH效应，不具有显著的杠杆效应。这也表明，对于这三个城市来说，有效信息对房地产市场正冲击和负冲击对房地产价格波动的影响是一样的，也就可以预期利好消息和利空消息对房地产价格波动性的影响是没有差别的，因此，无论利率是上升还是下降，都不会对这三个城市的房地产价格产生大的影响和效用，因而，利率政策对这三个城市是失效的。这也意味着，这三个城市是投机者在房地产市场上进行投机活动的首选之地，投机现象比较严重，而且投资者的交易行为存在着明显的“羊群效应”，从众心理和盲目投资的现象比较明显，这与一线城市最近几年居民房地产投资热情高涨，房价虚高，房地产泡沫严重的现象相一致。此外，利率的非市场化导致利率对市场变化的反应度不够，同时利率政策制定过程中受到诸多人为主观因素的影响，不能及时准确地根据市场情况进行调整，也是利率调节失效和房地产价格波动不具有非对称性的重要原因。

然而，北京市的房地产价格波动在1%的水平上显著，表现出了非常明显的杠杆效应，当出现利好消息时，该冲击会给北京房地产市场带来一个α＝0．115 149倍的冲击，而当出现利空消息时，该冲击会给北京房地产市场带来α＋γ＝－0．131 259倍的冲击，所以利空消息比利好能够带来更大的波动和冲击。由于TARCH项的系数γ是负的，因此所带来的冲击是减少北京房地产价格的波动。而且，由于ARCH项、TARCH项和GARCH项三者之和为0．929 108，接近于1，进一步表明利空消息和利好消息对北京房地产价格所产生的冲击是较为持久的。北京房地产价格波动具有杠杆效应而另外三个一线城市没有，这可能的原因在于虽然北京的房地产市场也存在房价虚高和投机现象，货币政策调节同样也存在失效现象，但北京作为首都和全国的行政中心，针对房地产市场而进行的宏观调控和行政调控手段比其他任何一个城市都更多更严厉，因而效果也更为显著和有效，杠杆效应也就更为显著。

对模型进一步进行条件异方差的ARCHLM检验发现，四个一线城市在1%、5%和10%的水平上不显著，不能拒绝原假设，意味着模型的残差序列不再存在ARCH效应，说明利用TARCH（1）模型消除了条件异方差。

（二）二线城市房地产价格波动的集聚性和杠杆效应

近几年随着经济的发展，更多的二线城市开始崛起，并对经济发展发挥了助推器的作用，带动了三线城市和周边区域的发展。二线城市的城市环境、产业功能配套以及开发的综合成本相对较低，因此逐渐变成了投资的最佳临界点，这让二线城市越来越具有吸引力。随着二线城市房地产市场逐渐趋于成熟，以及受到一线城市房地产价格高速上涨的影响，加之房地产投资者的投资活动从一线城市开始转向二线城市，种种原因导致二线城市的房地产价格上涨，二线城市也逐渐成为调控中的重点关注对象。鉴于此，本文在分析了一线城市的房地产价格波动之后，从二线城市中选取了青岛、长沙、大连、郑州、成都和西安六个城市，进一步分析二线城市房地产价格波动的非对称效应，模型结果见表3。

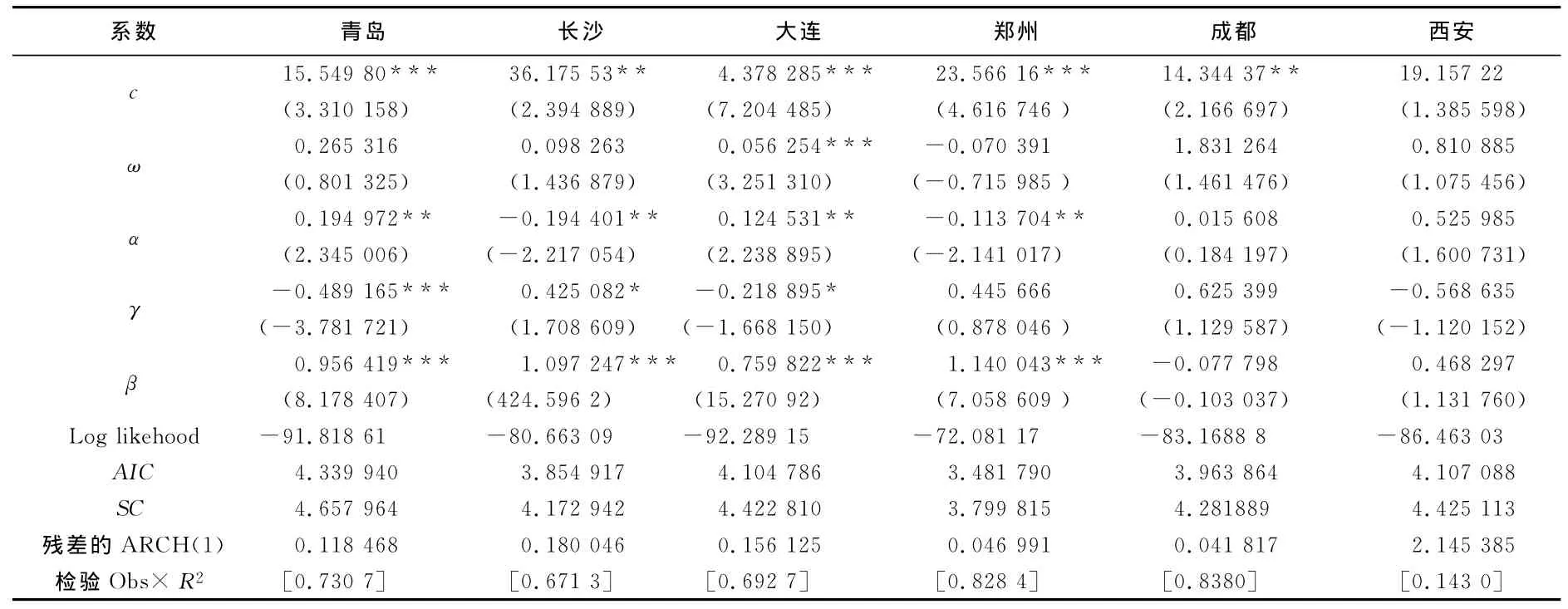
表3 二线城市房地产价格波动的TARCH模型结果

由表3可知，青岛、长沙、大连和郑州四个城市的α项在5%的水平上显著，表明这四个城市存在显著的ARCH效应，房地产价格波动具有集聚性，然而成都和西安的α项在1%、5%或者10%的水平上都不显著，房地产价格没有显著的波动集聚性，集聚效应不显著。这可能的解释在于，成都和西安地处内陆，交通远远没有其他几个城市方便，经济发展不足，市场经济相对于其他四个城市来说还存在很大的差距，同时，这两个城市的房地产市场发育程度也不足，居民购房大多是用于自己居住而非进行投资或者投机，刚性需求大，投机现象并不严重，因此，成都和西安虽然也是宏观调控的重要区域，但是房地产价格的波动没有显著的集聚性。由于成都和西安两个城市的房地产价格波动没有集聚性，因此我们在下文的非对称性分析中就不再讨论成都和西安。

通过对γ项的分析可知，青岛房地产价格波动的γ项在1%的水平上显著，表现出强烈的TARCH效应，房地产价格波动存在杠杆效应，利率调节在青岛的房地产市场上具有一定的效用。当出现利好消息时，该冲击会给青岛房地产市场带来一个α＝0．194 972倍的冲击，而当出现利空消息时该冲击会给杭州房地产市场带来α＋γ＝－0．294 193倍的冲击，所以利空消息比利好消息能带来更大的波动和冲击。由于TARCH项的系数γ是负的，因此所带来的冲击是减少青岛房地产价格的波动，ARCH 项、TARCH 项和GARCH项三者之和为0．662 226，表明利空消息和利好消息对青岛房地产价格波动所产生的冲击较持久。同样的，长沙和大连房地产价格波动的γ项在10%的水平上显著，存在杠杆效应，意味着利率调节在这两个城市同样具有一定的效果。当出现利好消息时，该冲击分别会给长沙和大连的房地产市场带来－0．194 401倍和0．124 531倍的冲击，而当出现利空消息时，则分别会会给长沙和大连的房地产市场带来0．230 681倍和－0．094 364的冲击，对于长沙房地产价格波动，利好消息产生的冲击更大，而对大连的房地产价格波动利空消息比利好消息产生更大的冲击。长沙的TARCH项系数为正，因此所带来的冲击是增加长沙的房地产价格波动，而大连的TARCH项的系数是负的，因此所带来的冲击是减少大连房地产价格的波动。由于ARCH项、TARCH项和GARCH项三者之和分别为1．327 928和0．665 458，大于或者接近于1，表明消息变动对长沙和大连的房地产价格产生的冲击是持久的。这可能的解释是，青岛、长沙和的大连都处于经济较为发达的地区，房地产市场发育比较成熟，是政府宏观调控的重点区域，而且这几个城市的投机现象和房地产泡沫也没有一线城市严重，刚性需求和投资需求较为平衡，因此，青岛、长沙和大连的房地产价格波动表现出非对称效应。

然而，郑州的γ项在显著水平上不显著，没有表现出强烈的TARCH效应，说明郑州房地产价格波动没有显著的杠杆效应，利率调节在郑州的房地产市场上市失效的。这可能的原因在于，郑州近年来房价虽然上涨幅度较大，房地产发展速度较快，但是整体经济发展水平还不够，房地产市场发育相较于东部的二线城市还远未达到成熟和完善，市场机制的作用还未得到充分发挥，对利率等货币政策的敏感度还不够；其次，郑州虽然也是政府进行宏观调控的对象，但是由于社会经济落后于一线城市以及东部沿海二线城市等导致两地的调控力度不够；最后，利率的非市场化也是导致郑州房地产价格波动没有显著杠杆效应的重要原因。

同样地，最后对模型进一步进行条件异方差的ARCH－LM检验发现，所选取的六个二线城市在1%、5%和10%的水平上均不显著，不能拒绝原假设，意味着这六个城市模型的残差序列不再存在ARCH效应，利用TARCH（1）模型消除了条件异方差。

四、结 论

通过以上分析，实证研究结论如下：第一，一线城市的房地产价格具有显著的波动集聚性，这与一线城市房价波动剧烈、投机现象严重等事实相吻合；第二，东中部的二线城市房地产价格具有显著的波动集聚性，但地处西部内陆的二线城市则波动集聚性不显著，这与整体经济发展水平、房地产市场成熟度、市场投机程度和房屋刚性需求有很大的关系；第三，除北京外的其他三个一线城市的房地产价格波动不具有显著的杠杆效应，利空消息和利好消息对房地产价格波动的影响是没有差别的；第四，东部沿海地区和长三角地区的二线城市具有显著的杠杆效应，利空消息和利好消息对其房地产市场的冲击较为持久，但是二线城市中的其他地区则不具有杠杆效应，消费者对利空消息和利好消息的敏感度较弱；第五，市场投机、房地产泡沫、利率非市场化、刚性需求等因素是影响一线和二线城市房地产价格波动杠杆效应的重要因素。

因此，实行差别化的组合的货币政策，尽早实行利率市场化，是实现房地产市场调控的较佳选择，单一的利率政策调控已不能够达到促进房地产市场稳定发展的目的。同时，也要采取措施抑制市场投机活动，鼓励和支持住房刚性需求，将经济手段与行政手段相结合，才能够保证我国房地产市场的健康发展。

注释：

① 一线、二线和三线城市的概念最早起源于房地产市场，政治地位 、经济实力、城市规模 、区域辐射力是划分一线、二线、三线城市的主要标准。一线城市包括北京、上海、深圳和广州四个城市，二线城市主要包括计划单列市、副省级城市、省会城市和经济发达底蕴深厚的城市。一线城市和二线城市都属于大中城市，房地产价格普遍较高，而且房地产销售量和成交量都非常大，因此，在房地产市场上具有较多的同质性。

［1］Dolde W，Tirtiroglue D W．Temporal and Spatial Information Diffusion in Real Estate Price Changes and Variances［J］．Real Estate Eco n，1997，25（4）：539－565．

［2］Guirguis H，Gianniko S，Garcia G．Price and volatility spillovers between large and small cities：A study of the Spanish market［J］．Journal of Real Estate Portfolio Management，2007，13：311－316．

［3］Kathy Szu－Yin Hung，Glascock John L．Volatilities and momentum returns in real estate investment trusts［J］．Real Estate Finance Economics，2010，41，：126－149．

［4］Kim Hiang Liow，Wei Chen．Is There volatility convergence in asia－pacific securitized real estate Markets？［J］．Real Estate Finance Economics，2011，47（2）：370－390．

［5］Miles W．Volatility clustering in U．S．home price［J］．The Journal of Real Estate Research，2008，30（1）：73－90．

［6］吴燕华，杨 刚．我国货币政策对房地产价格调控的动态影响分析［J］．现代财经，2011（10）：70－76．

［7］刘 轶，史运昌．热钱对房地产价格的影响：基于京、沪、穗、深圳数据的实证研究［J］．广东金融学院学报，2009（6）：42－50．

［8］时 鹏，余 劲．货币供应量、地价与房价关系的再检验：以陕西为例［J］．西北农林科技大学学报：社会科学版，2012（6）：124－129．

［9］车欣薇，郭 琨，李 斌，等．中国金融中心城市房地产价格与银行信贷的关系［J］．系统工程理论与实践，2011（4）：663－671．

［10］刘洪玉，杨振鹏．基于GARCH与 Markov转换模型度量房价波动风险［J］．清华大学学报：自然科学版，2012（2）：199－204．

［11］徐 轲，马永开，邓长荣．中国住房价格波动聚集性研究及短期预测［J］．管理学报，2010（6）：943－948．

［12］孟卫东，宋丽伟，阳 军．基于GARCH 模型的沪深地产股波动性分析及预测［J］．统计与决策，2010（12）：68－71．

［13］Tae Hyup Roh．Forecasting the volatility of stock rrice Index［M］．Springer Berlin Pressed，2006：424－435．

［14］Xu Yue，Pang Sulin．Correlation Analysis of Yield and Volatility Based on GARCH Family Models［M］∥Modeling Risk Management for Resources and Environment in China，Computational Risk Management，2011：527－537．

［15］Xing Jingli．The research on stock market volatility in china based on the model of ARIMA－EARCH－M（1，1）and ARIMA－TARCH－M （1，1）［C］．Education and Management International Symposium，2011：521－527．

［16］陈浪南，黄杰鲲．中国股票市场波动非对称性的实证研究［J］．金融研究，2002（5）：67－73．

［17］李卢霞．中国股票市场行业波动非对称性的实证研究［J］．经济经纬，2008（3）：13．

［18］Bolleslev，Chou and Kroner．ARCH modeling in finance：A review of the theory and empirical evidence［J］．Journal of Econometrics，1992，52：5－59．

［19］陈工孟，芮 萌．中国股票市场的股票收益与波动关系研究［J］．系统工程理论与实践，2003（10）：12－22．