球对称梯度折射率介质中光线传输轨迹的计算

石市委，王佩红，杨群，张苗，刘泉，孙兆奇

（安徽大学物理与材料科学学院，安徽合肥230039）

球对称梯度折射率介质中光线传输轨迹的计算

石市委，王佩红，杨群，张苗，刘泉，孙兆奇

（安徽大学物理与材料科学学院，安徽合肥230039）

通过将二阶的光线微分方程降阶为一阶微分方程组，并用四阶的Runge-Kutta方法对微分方程组进行迭代求解，从而求出球梯度折射率介质中的光线传输轨迹.该方法精确度高，适用于任意梯度分布的球梯度介质中的光线传输轨迹的计算.

梯度折射率；光线方程；光线轨迹

梯度折射率光学介质因其具有均匀折射率光学介质不能比拟的优异性能，近几十年来受到广泛关注[1].在折射率梯度分布的介质中，光线的传输轨迹不再是直线，而是按照光线微分方程的约束沿曲线轨迹传输[2].光线微分方程是二阶的矢量微分方程，通常只有极少数的几种梯度折射率分布曲线才有此方程的解析解，如Maxwell鱼眼透镜模型、Lunerburg透镜模型等[1-3].对于任意梯度的折射率分布介质，很难通过求解解析解的方法获得，通常是通过将微分方程降阶为两个一阶的微分方程组，然后通过严格的数值计算来求解[4].此过程在光学设计中被称为光线追迹，该过程的具体实施是较为复杂的.在通常的光学教材中，往往只是给出非常简单的过程框架，学生很难通过这些框架自行推导出整个迭代计算的过程.为弥补教材中的不足，本文将这种计算过程具体化，以球梯度介质为计算对象，使用四阶的Runge-Kutta（R-K）方法对微分方程组进行迭代求解，从而计算球梯度折射率介质中的光线传输轨迹.该方法精确度高，适用于对任意梯度分布的球梯度介质进行光线传输轨迹的计算，对本科生和研究生在光学课程学习或梯度折射率器件的研究时进行简单的梯度折射率器件性能的计算也有帮助.

1 光线追迹迭代公式的推导

光线在梯度折射率介质中传输必须依照光线微分方程进行，光线方程为[1]：

这是一个二阶微分方程，式中r⇀为描述光线轨迹的位置矢量，s为光线路程，n为光线所到达位置的折射率值.对球对称梯度折射率介质，n可表示为r的函数，即n(r).目前已知的球对称梯度折射率介质模型中，仅有Maxwell鱼眼模型和Luneburg介质模型有上述光线方程的解析解，其他的球对称梯度折射率分布模型均不具备解析解，必须通过对光线方程进行数值计算求解才能得到光线的传输轨迹.在对光线方程的数值计算过程中，通常的做法是将其降阶为一阶的微分方程，然后通过迭代计算进行求解.

(i)光线方程的降阶

光线方程可等价写成如下形式：

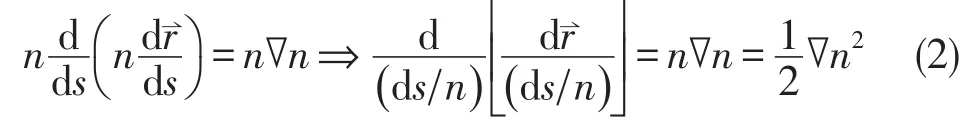
引入光学光线矢量T⇀，以及参量t和D⇀，它们被定义为：

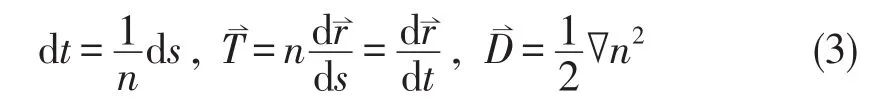
利用这些参量可将（2）式改写为

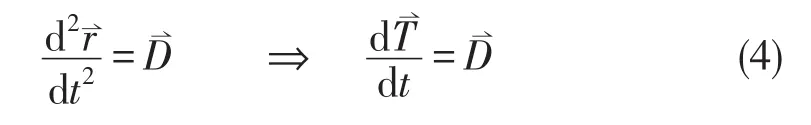
由几何光学理论可知，在球对称梯度分布介质中，光线的传输轨迹分布在一个确定的平面内，如图1所示.

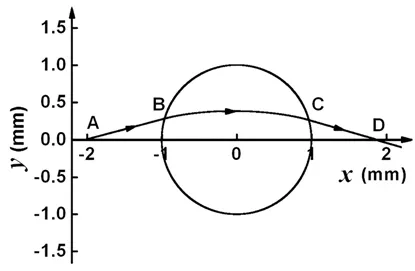
图1 光线在球对称梯度分布介质中的传输

因此，在球对称梯度分布介质中传输的光线可以定义在一个二维平面内，这里取x-o-y平面，则上述矢量均存在两个分量，它们可以用二元数组表示，即：

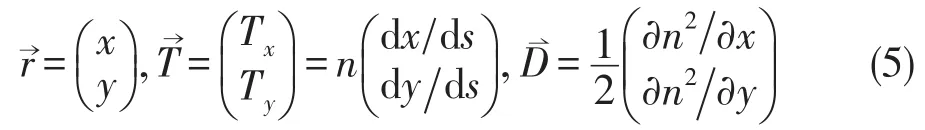
经前述过程，二阶的光线微分方程被转化为一阶的微分方程组[1]：

(ii)光线追迹的迭代关系式

前面得到的式（6）为存在迭代关系的一阶微分方程组，需联合求解.考虑到计算精度，采用Runge-Kutta（R-K）方法对式（6）进行展开.四阶的标准R-K方法形式为[5]：

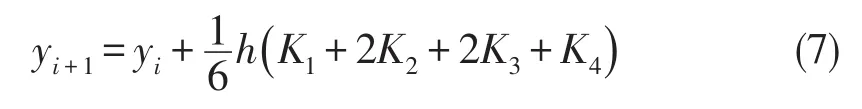
其中h为步长，各系数K1、K2、K3及K4为：

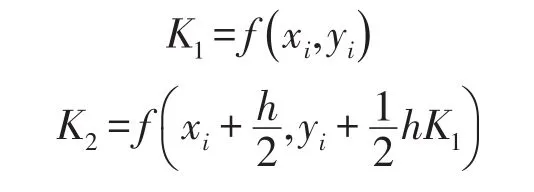
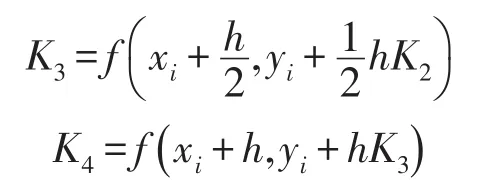
将式(6)写为如下形式：

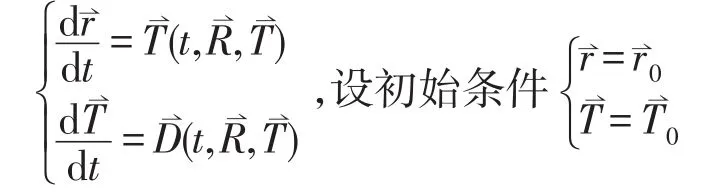
代入R-K方法的标准形式中，则有：

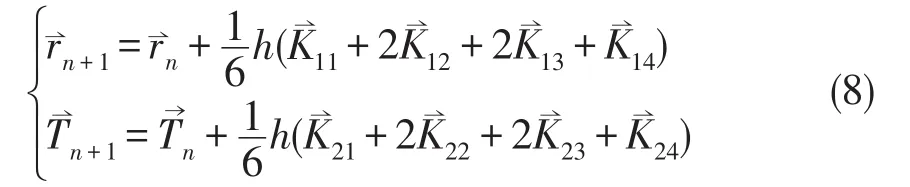
为了能与式（7）明显的对应起来，步长仍用h表示，这里h=Δt.其中各系数K的表达式如下，

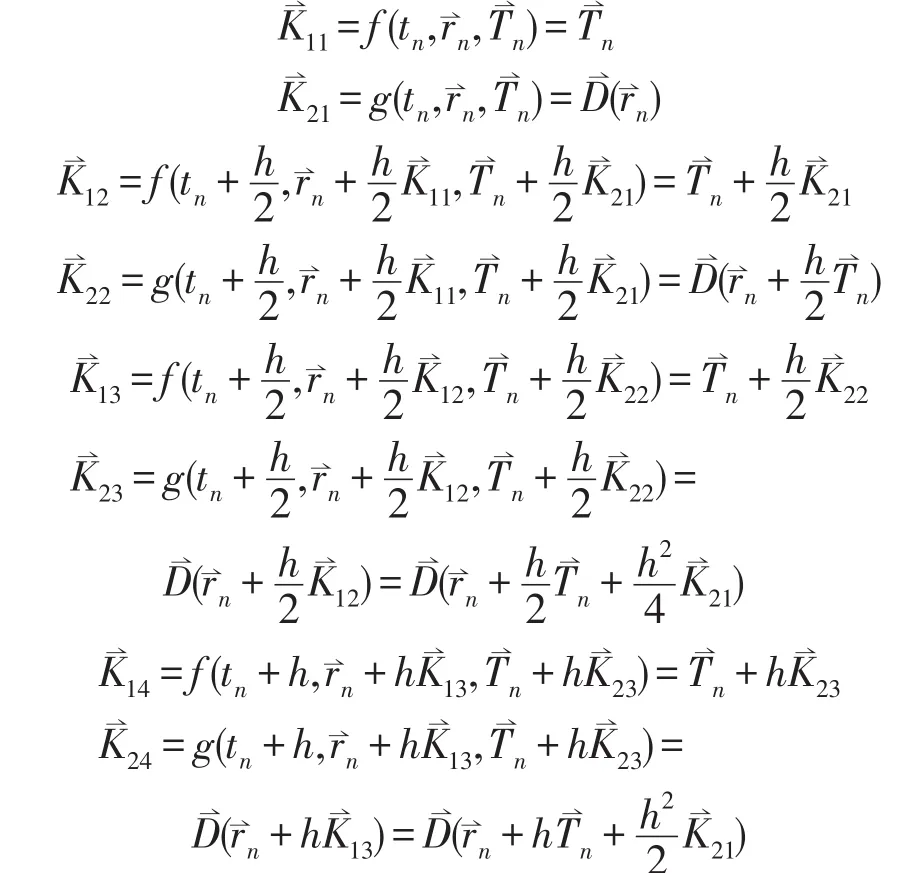
将以上K11，K12，K13，K14的结果代入式(8)中去，可以得到

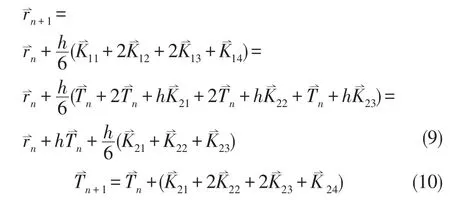
以上各式中的矢量可在直角坐标系中分解为分量形式，即：

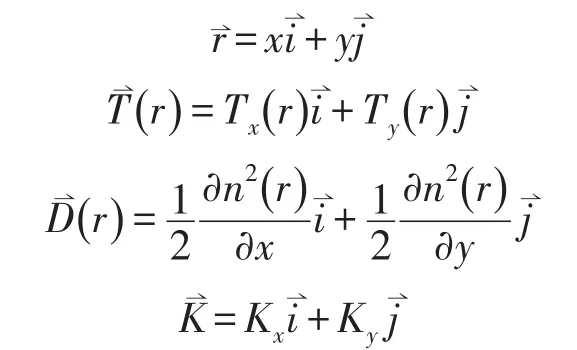
从(9)、(10)两式可以看出，如果已知光线在第n点处的坐标和光线方向，可以计算出、、和值，将其代入到(9)、(10)两式中，即可得到光线传播到的下一点的坐标和光线方向，重复此步骤，直到光线走出球梯度介质所在的范围.前述迭代方程组可使用C语言、Fortran语言或MATLAB软件编程进行迭代计算，从而计算出光线传输轨迹.

2 采用Luneburg透镜模型验证迭代公式的准确性

采用Luneburg透镜模型来检验前面所得到的光线追迹迭代公式的正确性和准确性.光线在Luneburg透镜模型中的传输轨迹存在解析解.因此，将由数值计算的结果同解析计算结果进行比较，可以知道前述光线追迹迭代公式的正确性和准确性.

Luneburg透镜模型的折射率分布公式为[1]：

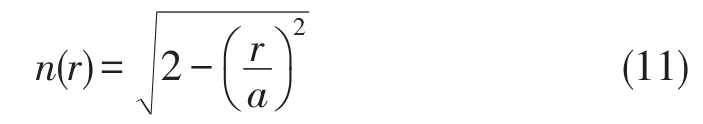
采用前面给出的数值计算过程所得到的计算结果如图2所示.高度不同的几条平行光线平行主轴入射，在球内光线弯曲，然后相交与球面上的一点，此点同时也是球面与主轴的焦点.这个结果与Luneburg透镜的光学特性是吻合的.对具体数值进行分析，各光线与主轴的交点理论上应该是(1,0)点，实际的数值计算结果见表1.这里各条光线与主轴的交点位置与理论值相差只有10-6数量级，说明该计算方法完全满足一般光学设计的要求.

图2 Luneburg透镜模型的光线追迹结果

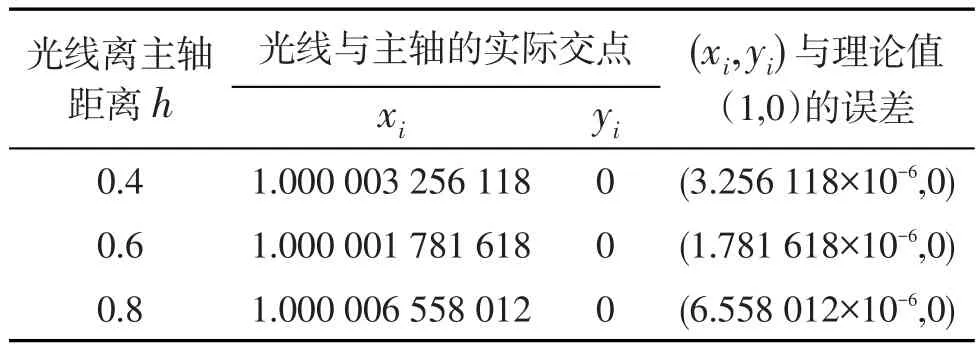
表1 对Luneburg透镜的光线追迹计算结果(单位：mm)

3 结论

给出一种在球对称梯度折射率介质中进行光线追迹的具体方法，并采用Luneburg透镜模型验证了该计算方法的正确性和准确性.该方法准确度高，且便于光学教学时使用.

[1]乔亚天.梯度折射率光学[M].北京:科学出版社,1991.

[2]刘德森.变折射率介质理论及其技术实践[M].成都:西南师范大学出版社,2005.

[3]Gomez-Reino C,PerezM V,Bao C.Gradient-index Optics:Fundamentals and Applications[M].Springer-Verlag Berlin and Heidelberg GmbH&Co.K,2002:98-121.

[4]易佑民,章于川,夏茹,等.梯度折射率微球回归反射材料的研究[J].光子学报,2003(32):425-428.

[5]吕同富,康兆敏,方秀男.数值计算方法[M].北京:清华大学出版社,2008:278-283.

【编校：许洁】

The Ray Tracing in Medium w ith Spherical Symmetry Gradient Refractive Index

SHIShiwei,WANGPeihong,YANGQun,ZHANGMiao,LIUQuan,SUN Zhaoqi
(SchoolofPhysics&Material Science,AnhuiUniversity,Hefei,Anhui230039,China)

By reducing the ray differential equation to lower order equations and using the fourth-order Runge-Kutta method,a ray tracingmethod was obtained for calculating the light trace inmedium with spherical symmetry gradient refractive index.Thismethod hashigh precision and can be used for ray tracing in any spherical symmetry gradient refractive index distribution.

gradient refractive index;ray differentialequation;ray tracing

O439

A

1671-5365(2014)12-0030-03

2014-08-13修回：2014-09-19

国家自然科学基金(51272001,51472003);安徽大学本科教育质量提升计划项目(xjtszy1401);安徽省教学研究项目(2012jyxm089);安徽大学校级本科教学工程教研项目(JYXM201330,XJJYXM14029,JYXM201234,JYXM201328,JYXM201204)

石市委（1978-），男，副教授，博士，研究方向为光电功能材料

时间：2014-09-23 14:11

http://www.cnki.net/kcms/detail/51.1630.Z.20140923.1411.001.html