CAT(0)空间中渐进非扩张映象的强收敛定理

董建，唐金芳

(宜宾学院数学学院，四川宜宾644007)

CAT(0)空间中渐进非扩张映象的强收敛定理

董建，唐金芳

(宜宾学院数学学院，四川宜宾644007)

在CAT(0)空间中对三个渐进非扩张映像构造了迭代算法，在适当的条件下证明了该算法强收敛于它们的公共不动点，所得结果推广了最近一些学者的研究结论.

CAT(0)空间；渐进非扩张映像；强收敛定理；公共不动点

设X是CAT(0)空间,用(1-t)x⊕ty表示连接x和y的测地线段中的唯一的点z,使得

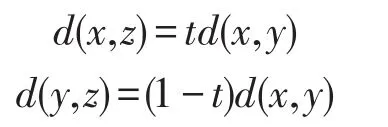
其中t∈[0,1].

Kirk[1]首先在CAT(0)空间中研究了不动点理论,证明了定义在完备的CAT(0)空间中的有界闭凸子集上的非扩张映像总是存在不动点的.从此以后, CAT(0)空间中各种映像的不动点理论的研究得到了迅速发展[2-7].

设E是Banach空间,K是E的非空闭凸子集, T:K→K是映像.Mann迭代序列定义如下:

其中n∈N,{} an是(0,1)中的序列.

进一步,Ishikawa迭代序列定义如下:

其中n∈N,{an}和{bn}都是(0,1)中的序列.

2007年,Agarwal等[8]在Banach空间E中证明如下的迭代序列的收敛性:

其中K是E的非空闭凸子集，n∈N,{an}和{bn}都是(0,1)中的序列.

2012年,Sahin A等[9]在CAT(0)空间中得到了如下的结论：设K是完备的CAT(0)空间X的非空闭凸子集,T:K→K是{} un渐进拟非扩张映像,满足T的不动点集F(T)≠φ且.定义序列{} xn如下:

其中n∈N,{an}和{bn}都是(0,1)中的序列.如果或者,其中,那么序列{xn}强收敛到T的一个不动点.

受上述文献的启发,本文在CAT(0)空间中对三个渐进非扩张映像构造迭代算法,在适当的条件下证明了该算法强收敛于这三个渐进非扩张映像的公共不动点.

1 预备知识

设(X,d)是度量空间,K是X的非空闭凸子集.称映像T:K→K是非扩张的,如果对任意的x,y∈K有

称映像T:K→K是具系数{} un的渐进非扩张映像,如果存在[0,+∞)中的序列{un}满足使得对任意的x,y∈K,任意的n∈N有

称映像T:K→K是L-Lipschitzian的,如果存在常数L＞0使得对任意的x,y∈K都有

称映像T:K→K是一致L-Lipschitzian的,如果存在常数L＞0使得对任意的n∈N,任意的x,y∈K都有

显然,渐进非扩张映像一定是一致L-Lipschitzian映像.

称映像T:K→K满足条件(I),如果T的不动点集F(T)≠φ并且存在一个单调不减的函数f:[0,∞)→[0,∞)满足f(0)=0,f(r)＞0,∀r∈(0,∞),使得对任意的x∈K有

引理1.1[10]设X是CAT(0)空间,对任意的t∈[0,1],任意的x,y,z∈X,下列不等式成立:

引理1.2[11]设X是CAT(0)空间,任取x∈X,序列{tn}⊂[b,c]满足b,c∈(0,1)及0＜b(1-c)≤.如果X中的序列{xn}和{yn}满足

引理1.3[12]设{an},{bn}和{} cn都是非负实数序列,满足如果,那么极限存在.

2 主要结果

定理2.1设K是完备的CAT(0)空间X的非空闭凸子集,T,S,R是三个分别具系数{ln},{kn},{un}的渐进非扩张映像,映像S满足条件(I).对任意的x1∈X,定义序列{xn}如下:

其中{αn},{βn},{γn}都是[b,c]中的序列，满足b,c∈(0,1)及0＜b(1-c)≤.如果

并且

那么序列{} xn强收敛到Γ中的一点.

事实上,对任意的p∈Γ,有

和

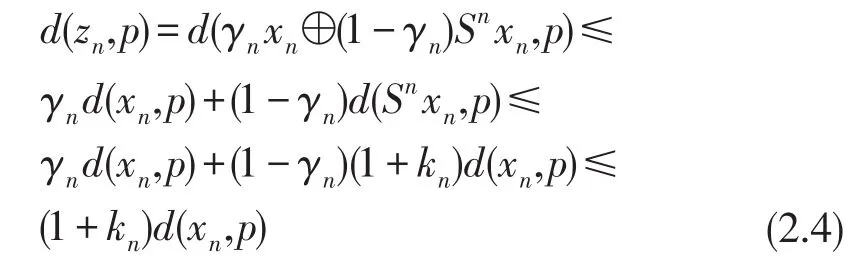
记bn=ln+kn+un+knun，由(2.1)(2.3)(2.4)得

如果c=0,那么定理2.1的结论显然成立.下面考虑c≠0的情况.

事实上,对任意的p∈Γ,由(2.3)(2.4)得

两边取上极限得

和

注意到R是{} un渐进非扩张映像,由(2.7)得

两边取上极限得

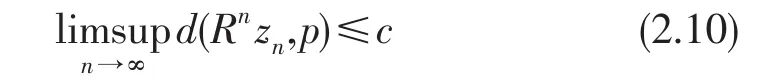
由(2.1)和(2.6)得

由引理1.2和(2.8)(2.10)(2.11)得

由(2.5)得

两边取下极限得

由(2.9)和(2.13)得

这表明

注意到S是{} kn渐进非扩张映像,所以

两边取上极限得

由引理1.2和(2.6)(2.14)(2.15)得

由(2.5)得

两边取下极限,由(2.12)得

由(2.8)和(2.17)得

这表明

注意到T是{} ln渐进非扩张映像,所以

两边取上极限得

由引理1.2和(2.6)(2.18)(2.19)得

由(2.1)有

由(2.12)和(2.20)得

注意到

由(2.16)(2.21)得

第三步,证明序列{} xn是K中的Cauchy序列.

因为f:[0,∞)→[0,∞)是单调不减函数，且满足f(0)=0,f(r)＞0,∀r∈(0,∞)，所以

于是

从而对任意的ε＞0,存在自然数n0,当n＞n0时,有

此时,必存在p1∈Γ,当n＞n0时,有

当n＞n0时,对任意的自然数m,由(2.23) (2.26)有

这表明序列{xn}是K中的Cauchy序列.由于K是完备的CAT(0)空间X的非空闭凸子集,所以序列{xn}一定收敛于K中的一点,不妨设

其中q∈K.

第四步,证明q∈Γ.

事实上,对任意的ε＞0,由(2.27)知存在自然数n1,当n＞n1时,有

由(2.25)知存在自然数n2,当n＞n2时,有

注意到

由(2.28)(2.29)知对任意的ε＞0,当n＞max{n1,n2}时,有d(Sq,q)＜ε.由ε的任意性知d(Sq,q)=0,即 q∈F(S).用相同的方法可证q∈F(T)和q∈F(R).故q∈Γ.

这就完成了定理2.1的证明.

[1]Kirk W A.Geodesic geometry and fixed point theory II[C].InternationalConference on Fixed Point Theory and Applications,Yokohama Publications,Yokohama,Japan,2004:113-142.

[2]Shahzad N,Markin J.Invariantapproximations for commutingmappings in CAT(0)and hyper convex spaces[J].Journal ofMathematicalAnalysisand Applications,2008,337(2):1457-1464.

[3]Leustean L.A quadratic rate of asymptotic regularity for CAT(0) spaces[J].Journal of Mathematical Analysis and Applications, 2007,325(1):386-399.

[4]Shahzad N.Fixed point results formultimaps in CAT(0)spaces[J]. Topology and Its Applications,2009,156(5):997-1001.

[5]Tang JF,Chang SS,Lee HW Jet al.Iterative algorithm andΔ-convergence theorems for total asymptotically nonexpansive mappings in CAT(0)spaces[J].Abstract and Applied Analysis,2012, Article ID 965751.doi:10.1155/2012/965751.

[6]Khan A R,KhamsiM A,Fukhar-ud-din H.Strong convergence of a general iteration scheme in CAT(0)spaces[J].Nonlinear Anal.2011,74(3):783-791.

[7]Tang JF.The strong convergence theorem of asymptotically quasinonexpansive non-self mappings in CAT(0)spaces[J].Journal of Yibin University,2013,13(6):1-3.

[8]Agarwal R P,O’Regan D,Sahu D R.Iterative construction of fixed points of nearly asymptotically nonexpansivemappings[J].NonlinearConvex Anal,2007,8(1):61-79.

[9]Sahin A,BasarirM.On the strong convergence ofamodified S-iteration process for asymptotically quasi-nonexpansivemappings in a CAT(0)space[J].Fixed point theory applications,2013.doi: 10.1186/1687-1812-2013-12.

[10]Dhompongsa S,Panyanak B.OnΔ-convergence theorems in CAT(0)spaces[J].ComputMath Appl,2008(56):2572-2579.

[11]Nanjaras B,Panyanak B.Demiclosed principle for asymptotically nonexpansive mappings in CAT(0)spaces[J].Fixed Point Theory and Applications,vol.2010,Article ID 268780,14 pages,2010.

[12]Nammanee K,Noor M A,Suantai S.Convergence criteria ofmodified Noor iterations with errors for asymptotically nonexpansive mappings[J].Journal of Mathematical Analysis and Applications, 2006,314(1):320-334.

【编校：许洁】

The Strong Convergence Theorem of Asym ptotically Nonexpansive Mappings In CAT(0)Spaces

DONG Jian,TANG Jinfang
(SchoolofMathematics,Yibin University,Yibin,Sichuan 644007,China)

The algorithm for solving the common fixed point problem of three asymptotically nonexpansivemappingswas studied in CAT(0)spaces.Under suitable conditions the strong convergence theorem to approximating a common fixed pointof three asymptotically nonexpansivemappingswas proved.The results extend and improve the corresponding resultsannounced by some others.

CAT(0)spaces;asymptotically nonexpansivemappings;strong convergent theorem;common fixed point

O177.5

A

1671-5365(2014)12-0007-04

2014-05-26修回：2014-06-24

四川省教育厅项目(14ZA0271)；宜宾学院科研项目(2013YY06)

董建(1962-)，男，副教授，本科，研究方向为非线性分析和微分方程

时间：2014-06-27 14:20

http://www.cnki.net/kcms/detail/51.1630.Z.20140627.1420.001.htm l