关于一类新的弱奇性W endroff型积分不等式的注记
2014-07-20吴宇唐敏曾德宇
吴宇,唐敏,曾德宇
(1.宜宾学院数学研究所,四川宜宾644007;2.西南民族大学预科教育学院,四川成都610041;3.宜宾市第一中学校,四川宜宾644000;4.四川大学电子信息学院,四川成都610041)
关于一类新的弱奇性W endroff型积分不等式的注记
吴宇1,唐敏2,曾德宇3,4
(1.宜宾学院数学研究所,四川宜宾644007;2.西南民族大学预科教育学院,四川成都610041;3.宜宾市第一中学校,四川宜宾644000;4.四川大学电子信息学院,四川成都610041)
讨论了一类新的弱奇性Wendroff型积分不等式解的估计,所得结果推广了已有的相关结果,并将结果应用到研究微分方程解的有界性中.
弱奇异积分不等式;解的估计;两个变量;非线性
奇异积分不等式对常微、偏微及泛函微分方程问题的研究有重要的作用.大批学者的研究取得了一系列较好的成果[1-5].2008年Cheung[6]研究了一类含有两个变量的弱奇性Wendroff型积分不等式

2010年Wang[7]研究了较广的一类弱奇性Wendroff型积分不等式

2013年吴宇等[8]研究了一类新的弱奇性Wendroff型积分不等式

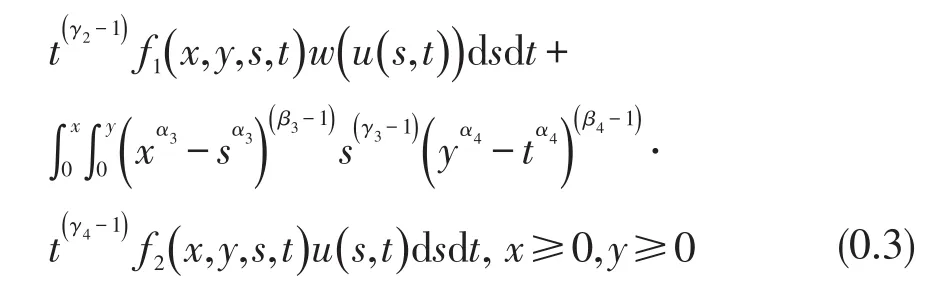
2013年曾德宇等[9]研究了较广的一类弱奇性Wendroff型积分不等式

基于文[8]、[9]的工作,考虑更广的一类新的弱奇性Wendroff型积分不等式
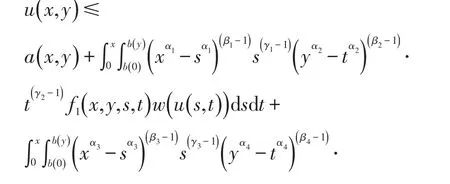

解的估计.本文给出的解的估计更具一般性.
1 预备知识
为方便论述,首先引入引理.
引理[3]若α,β,γ,p为正常数,则

符号说明:R=(-∞,+∞),R+=(0,+∞),C(X,Y)表示从X到Y的连续函数的集合,D1z(x,y)和D2z(x,y)表示分别对x和y的一阶偏导数.
2 主要结果
考虑不等式(0.5)且假设下列条件成立:
定理1若u(x,y)∈C(R2+,R)且满足弱奇性不等式
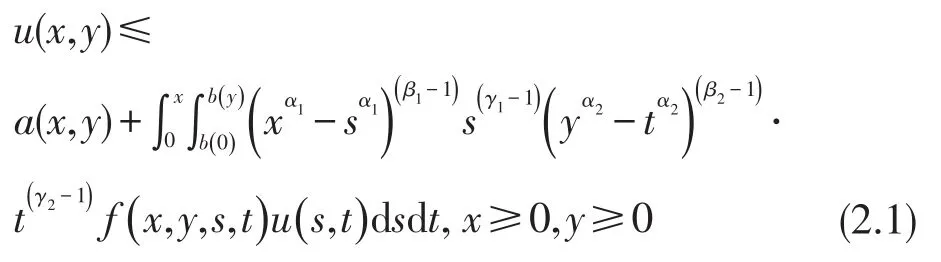
其中非负参数αi,βi,γi(i=1,2)满足条件(H),函数a(x,y)、f(x,y,s,t)、b(y)满足条件(L),则
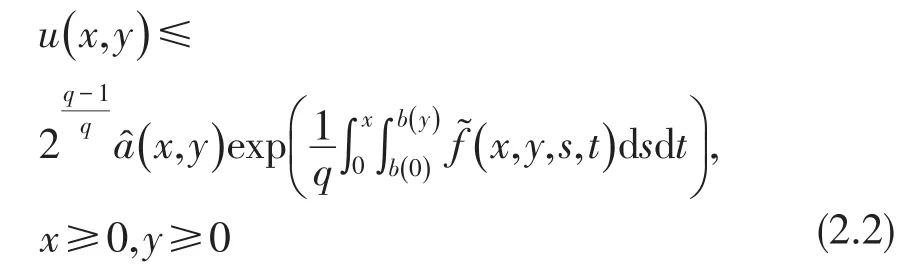
其中

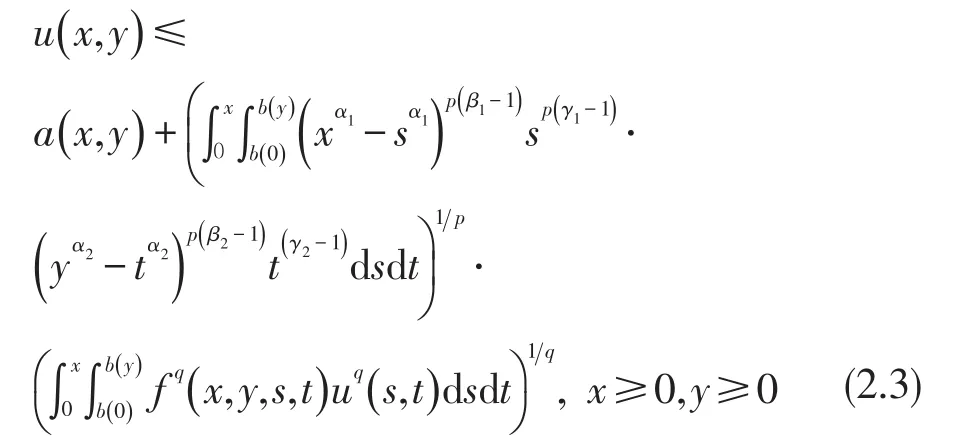
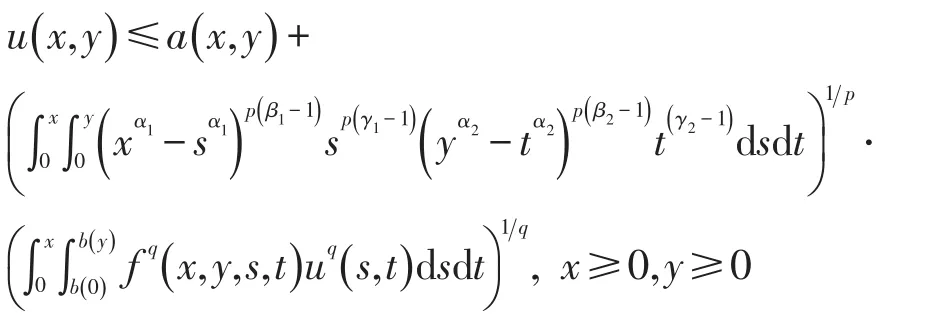
令

由本文引理得

(2.3)式可化为:
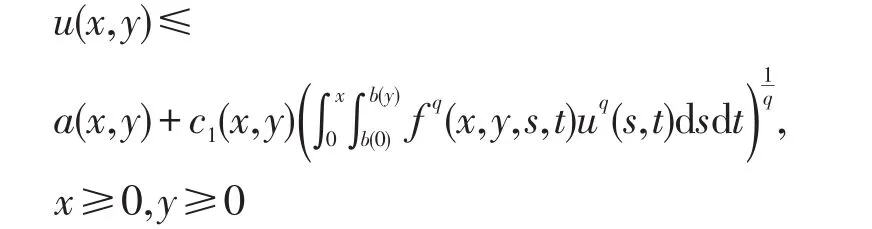
将上式两边q次方,应用文[2]中不等式“若n为正整数,而r(≥1),A1,…,An是非负数,则(A1+…+ An)r≤nr-1(+…+)”,可得

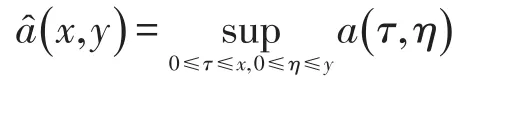
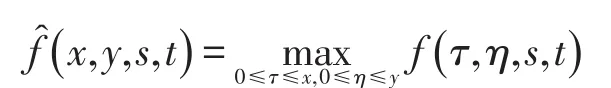


令

有uq(x,y)≤z(x,y),即u(x,y)≤z1q(x,y),由定理1中的定义可得且有
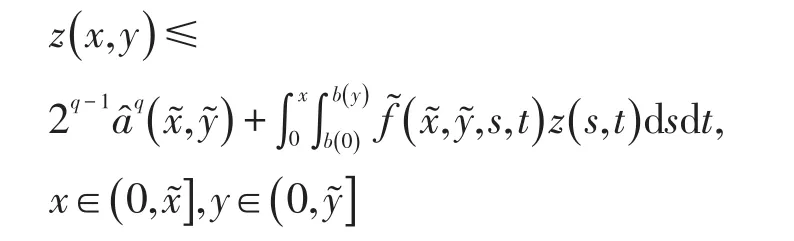
对z(x,y)关于x求偏导得
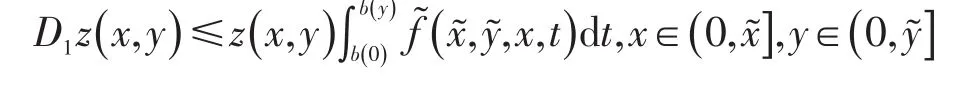
有

上式两边从0到x积分,得
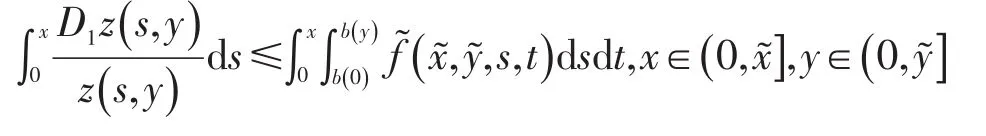
有
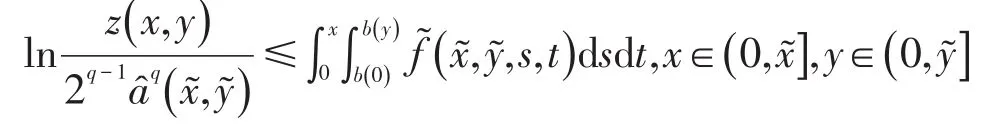
所以

由u(x,y)≤z1q(x,y)有

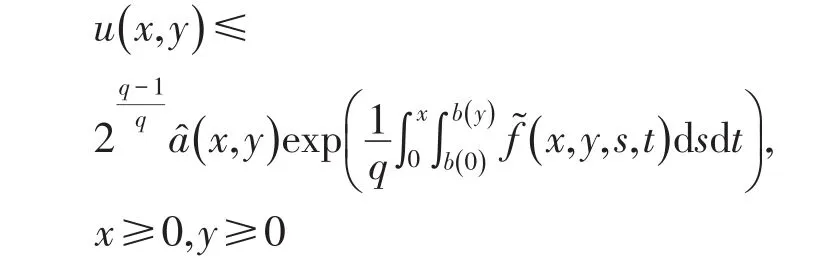
定理得证.
定理2如果u(x,y)∈C(R2,R)且满足弱奇异积分不等式(0.5),其中非负参数αi,βi,γi(i=1,2,3,4)满足条件(H),函数a(x,y)、b(y)、fi(x,y,t,s)(i= 1,2)、w(u)满足条件(L),则

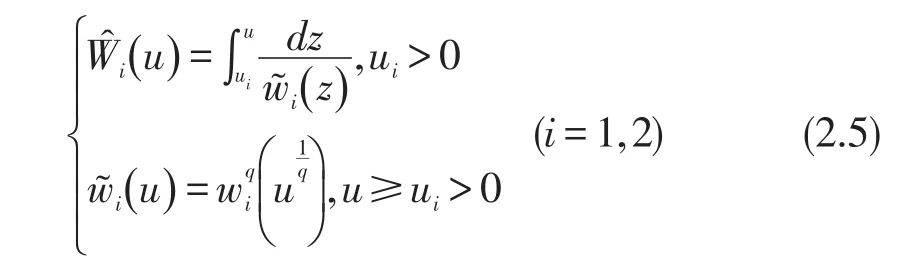
X,Y∈R+且为满足下式的最大值
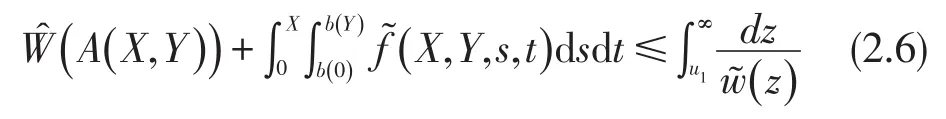



其中x≥0,y≥0.令

由本文定理1有
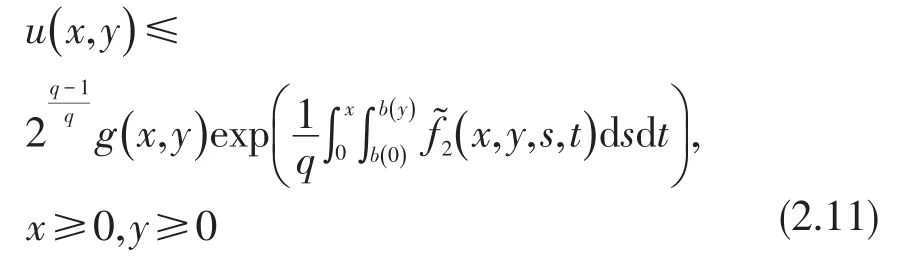
由b(x,y)的定义有u(x,y)≤g(x,y) b(x,y),即有


由0≤b(y)≤y,得
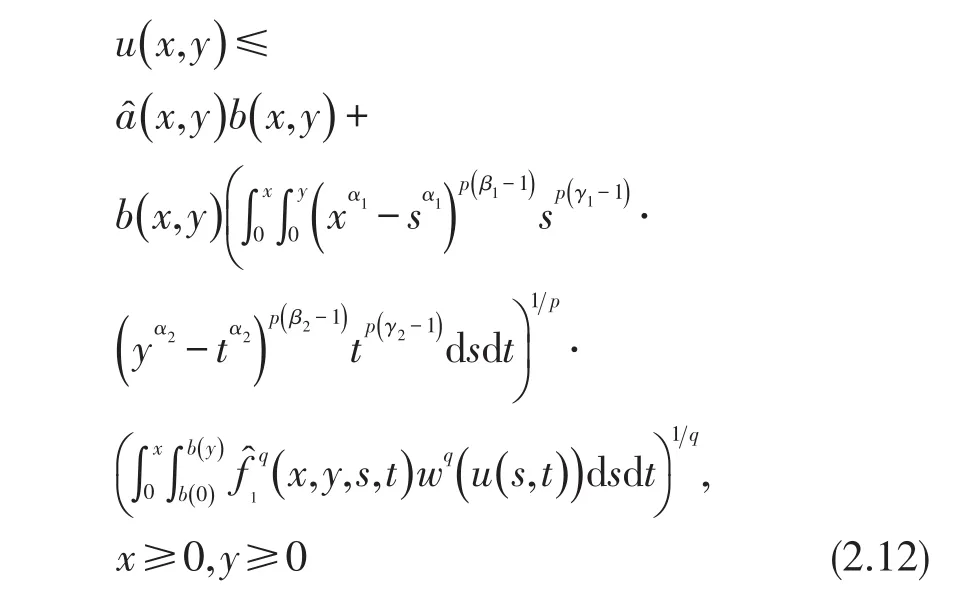
令

由本文引理得
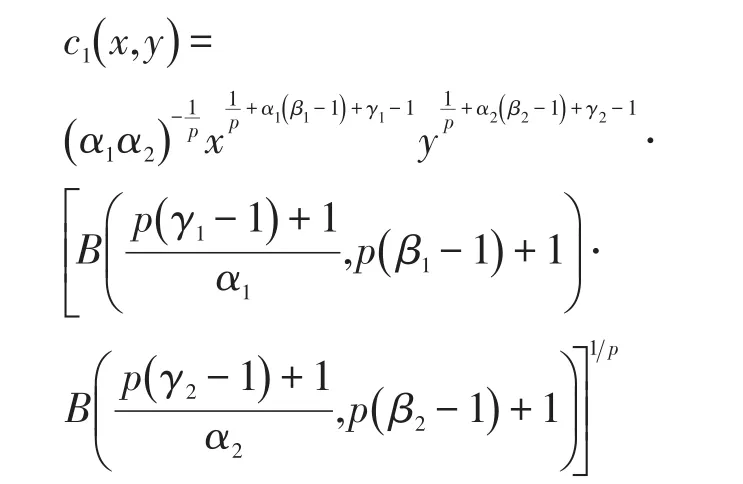
其中x≥0,y≥0.由(2.12)式有
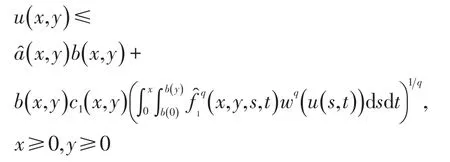
将上式两边q次方,应用文[2]中不等式“若n为正整数,而r(≥1),A1,…,An是非负数,则(A1+…+An)r≤nr-1(+…+”,可得
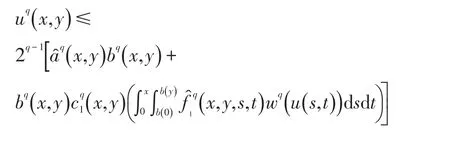



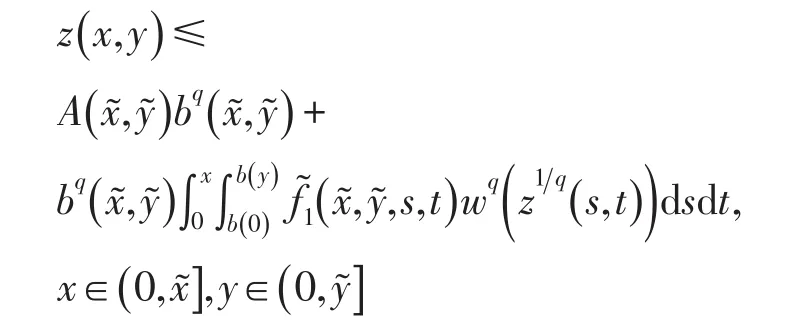
对z(x,y)关于x求偏导及利用0≤b(y)≤y单调不减及(u)的定义,w(u)关于u单调不减可得

所以

上式两边从0到x积分,得
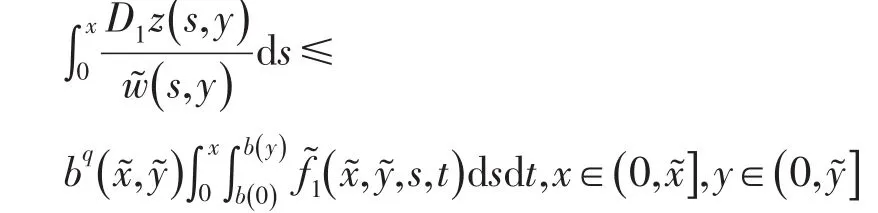

所以

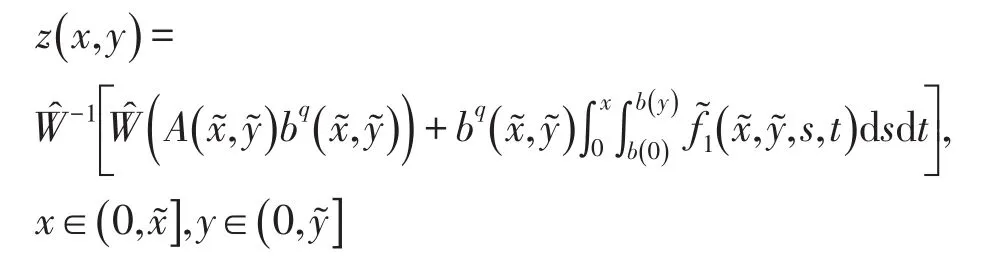
可得


其中x∈(0,X],y∈(0,Y].定理得证.
注:当b(y)≡y,f2(x,y,s,t)≡0时,才是文[9]所研究的情形.
3 在弱奇性微分方程中的应用
考虑

令α1=α2=1,β1=β2=,γ1=γ2=,由且p>1,可得1<p<2;
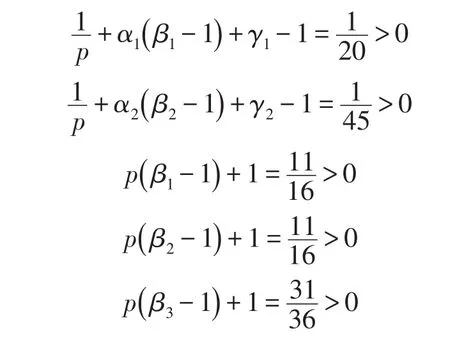

于是
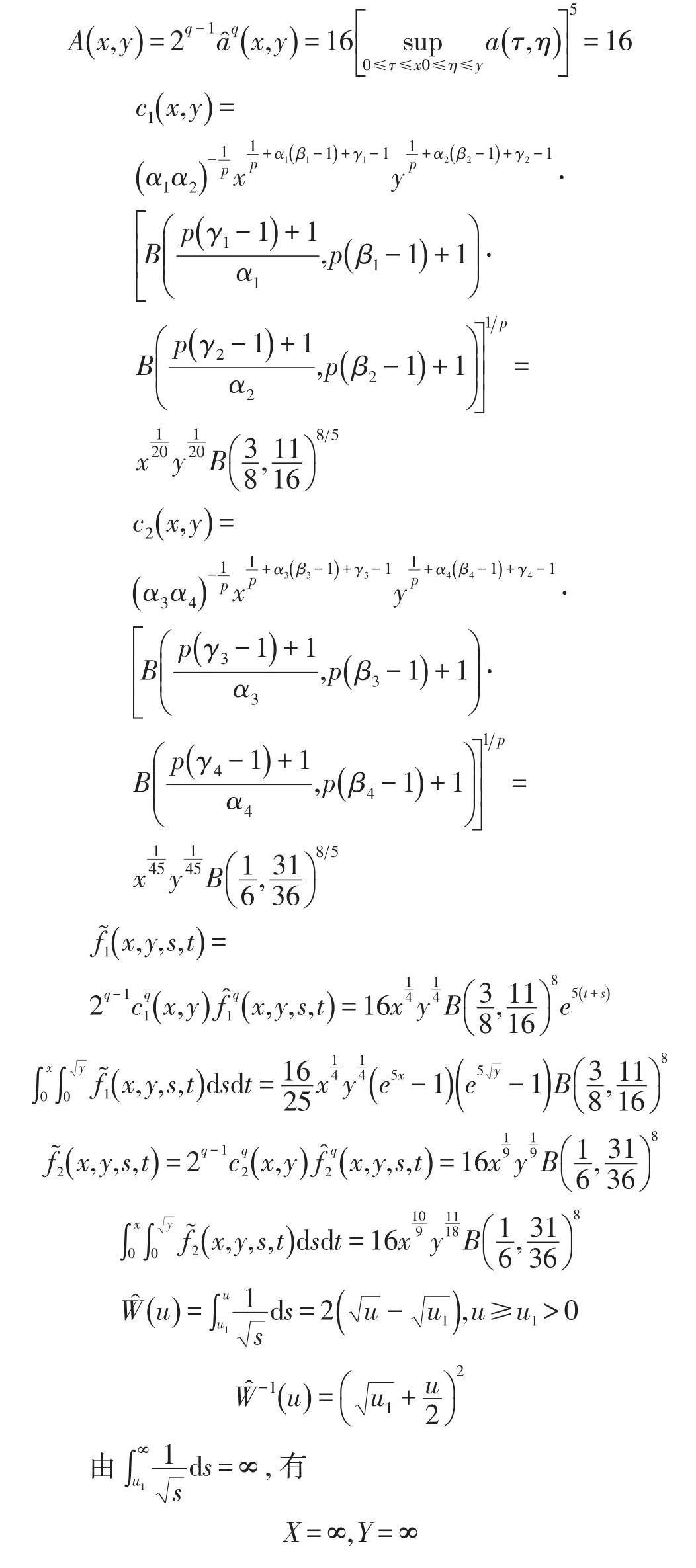

由本文定理2可得

其中x≥0,y≥0.表明不等式(3.1)中当x≥0,y≥0时,u(x,y)是有界的.
[1]Henry D.Geometric Theory of Semilinear Parabolic Equations[M]. New York:Springer-Verlag,Berlin,Heidelberg,1981.
[2]Medved M.A new approach to an analysisofHenry type integral inequalities and their Bihariversion[J].JMath Anal Appl,1997,214 (2):349-366.
[3]马庆华,杨恩浩.弱奇性Volterra积分不等式解的估计[J].应用数学学报,2002,25(3):505-515.
[4]吴宇,邓圣福.一类弱奇性Volterra积分不等式的推广[J].四川大学学报:自然科学版,2004,41(3):473-478.
[5]吴宇.一类新的弱奇性Volterra积分不等式[J].应用数学学报, 2008,31(4):584-591.
[6]CheungW S,Ma Q H,Tseng S.Some new nonlinearweakly singular integral inequalities ofWendroff typewith applicayions[J],Journal of Inequalities and Applicayions,2008,Article ID 909156,13 pages.
[7]Wang H,Zheng K,Som nonlinearweakly singular integral inequalities with two variables and applications[J].Journal of Inequalities and Applications,2010:12,Article ID 345701.
[8]吴宇,唐敏,周察金.一类新的弱奇性Wendroff型积分不等式解的估计[J].应用数学学报,2013,36(1):97-107.
[9]曾德宇,唐敏,吴宇.关于一类弱奇性Wendroff型积分不等式的注记[J].宜宾学院学报,2013,13(12):1-4.
【编校:许洁】
Estimateson Solutionsof a New W eakly SingularW endroff Integral Inequalities
WUYu1,TANGMin2,ZENGDeyu3,4
(1.Institute ofMathematical Science,Yibin University,Yibin,Sichuan 644007,China;2.School ofPreparatory Education, SouthwestUniversity forNationalities,Chengdu,Sichuan 610041,China;3.The First High School ofYibin,Yibin,Sichuan 644000,China;4.CollegeofElectronicsand Information Engineering,Sichuan University,Chengdu,Sichuan 610041,China)
Estimate on solutions of a new weakly singularWendroff integral inequalitieswere discussed,which generalized some known weakly singular inequalities for functions in two variables.Application example in the roundedness of the solution ofdifferentialequationwasalsogiven.
weakly singular integral inequality;estimateon solutions;two variables;nonlinear
O178
A
1671-5365(2014)12-0001-06
2014-04-10修回:2014-04-23
四川省教育厅重点项目(10ZA173);宜宾学院自然科学重点项目(2012S10)
吴宇(1958-),女,教授,理学学士,研究方向为积分方程与不等式
时间:2014-05-16 11:32
http://www.cnki.net/kcms/detail/51.1630.Z.20140516.1132.008.htm l
