改进的二维最小卡方散度图像分割方法
2014-07-19王晨樊养余熊磊
王晨,樊养余,熊磊
1.西北工业大学电子信息学院,西安 710072
2.空军工程大学航空航天工程学院,西安 710038
改进的二维最小卡方散度图像分割方法
王晨1,2,樊养余1,熊磊2
1.西北工业大学电子信息学院,西安 710072
2.空军工程大学航空航天工程学院,西安 710038
1 引言
图像分割作为图像分析和图像理解的基础,其性能关系到图像处理任务的成败,因此是图像处理领域研究的重要内容之一[1-3]。然而由于自然界的复杂性,目前还没有一种较为通用的图像分割技术。针对不同应用背景,相关研究人员先后提出了种类繁多的图像分割方法。在这些方法中,基于图像直方图信息的阈值化方法由于它的简洁有效性得到了众多研究人员的青睐[4]。在图像阈值化方法中,最为经典的方法如Otsu提出的最大类间方差法[5]、最小误差阈值化[6]、基于图像熵的方法[7-9]等。由于熵方法有着坚实的物理学背景,因此在图像处理领域得到了成功的关注。在熵方法中有一类称为交叉熵的方法是该类方法的一个强力分支,在图像阈值化分割中得到了成功的应用[10-12]。
但是,交叉熵阈值法因存在对数运算,导致其计算量较大,不便于许多实时场合的广泛应用。本文引入卡方散度来度量两个概率分布的差异程度,提出了新的基于卡方散度的图像阈值化分割准则。实验结果表明,基于卡方散度的图像阈值化分割准则是可行的,且计算所需时间量比交叉熵值法有了明显的减少。因此,在实时性要求较高的场合比较适宜。另外,基于卡方散度的阈值化分割方法在处理受到噪声干扰的图像时,可以比交叉熵法获得更好的分割结果。
2 基于卡方散度的分割方法
交叉熵[10],又称为相对熵或有向散度,用来度量两概率向量之间差异性。卡方散度[13]也可以用来度量两个概率分布的差异性程度。因此,本文将卡方散度用于图像阈值化问题。
2.1 卡方散度

在交叉熵的求取过程中含有对数运算,其计算量大,不利于实时性要求高的场合。本文利用卡方散度来度量两个概率分布间的差异程度[12-13]:

文献[12]说明了简单的基于卡方散度的图像分割会出现较多错分部分,丢失一部分图像原有的有用信息。因此本文提出一种基于改进的卡方散度的图像分割方法。
2.2 基于对称卡方散度的阈值化原理
设I是大小为M×N,灰度级为L的数字图像,I={f(x,y)|x∈{1,2,…,M},y∈{1,2,…,N},f(x,y)表示图像坐标(x,y)处的像素值。图像的归一化直方图可表示为H={h0,h1,….,hL-1},且0≤hi≤1。
图像进行阈值分割时,假设t是分割阈值,t把图像分割为两部分,其中灰度级{0,1,…,t}的像素值表示背景,{t+1,t+2,…,L-1}表示目标。
对于卡方散度而言,一般χ2(P|Q)不具有对称性,因此定义它的对称版本为:

在式(3)的基础上,本文构造了一种更为有效的图像阈值化方法。为了叙述方便,首先令:

把式(4)、(5)代入式(3),可以得到关于图像阈值化前后背景与目标的散度,即

定义阈值化前后图像总的散度为:

要获得最佳阈值,可对式(7)求极小值,即

其中t*表示最佳阈值。求出t*后,可用下式对原图像进行阈值化:
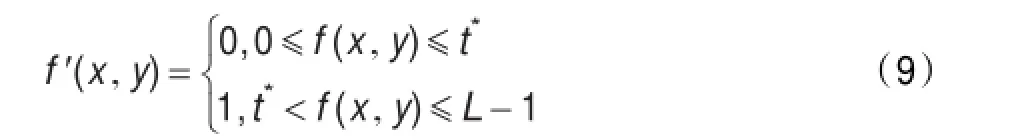
其中,f(x,y)、f′(x,y)分别表示原始图像、阈值图像坐标(x,y)处的像素值。
2.3 计算复杂性分析
假设计算机每次执行加法(减法)运算一次所需时间(单位:s)为t1,执行一次乘法或除法运算所需时间(单位:s)为t2,且t1<t2。文献[14]中详细分析了原始卡方散度与交叉熵的计算复杂性。因此,本文计算其对称卡方散度J(P|Q)所用的时间(单位:s)为4nt2+2(n-1)t1+t1。
所以,交叉熵比对称卡方散度的计算多花费时间(单位:s)为:(4kn+2n-1)t1+(k2n+4kn)t2。
3 改进的二维卡方散度分割方法
3.1 二维直方图的构建
假设一幅图像大小为M×N,灰度级为L,用f(x,y)表示原始图像,g(x,y)表示原始图像的均值滤波结果。设l(i,j)表示f(x,y)中灰度级为i且g(x,y)中灰度级为j的像素对个数,那么定义二元组(i,j)在图像和其邻域滤波图像中出现的联合概率:

其中,i=0,1,…,L-1;j=0,1,…,L-1。以上就是在二维直方图构建中出现最多的一种构建方法,即均值二维直方图[15],它是一个L×L的矩阵,如图1(a)所示。其中区域1和2代表目标和背景,区域3和4表示边缘点及噪声。
由于图像的均值滤波属于一种平滑处理,即低通滤波方式,一般被用来处理高斯噪声。均值滤波在平滑图像得到邻域平均灰度的同时,使图像变得模糊,而且滤波效果不佳,尤其对椒盐噪声滤波效果不如中值滤波。中值滤波法[1]则是一种非线性平滑技术,它是通过从图像中的某个采样窗口取出n个数据进行排序,然后用排序后的中值取代要处理的数据来实现抑制图像噪声的目的。这种方法在滤除噪声点的同时能够较好地保存图像的细节和边缘。
中值滤波和均值滤波通常被分别用来处理脉冲噪声和高斯噪声,当图像同时存在高斯噪声和脉冲噪声时,单独用哪种滤波方法都不会达到好的去噪效果。因此,本文选择文献[16]中采用的改进中值滤波方法对图像进行滤波,然后再利用滤波图像和原始图像构建新的二维直方图。
令w(x,y)表示新的原始图像滤波结果,又令g(x,y)= |f(x,y)-w(x,y)|,本文构建了如图1(b)所示的新的中值二维直方图。这种构建方法不仅使区域1,区域2尽可能地包含了所有目标点和背景点,同时也避免了常用的均值二维直方图及其区域划分方法中区域1和区域2可能存在边缘点和噪声点导致分割结果不准确的问题。

图1 二维直方图的构建方式
从图1(b)可看出,对于中值二维直方图,由于图像中目标和背景内像素点的邻域灰度绝对差较小,所占比例很大,因此,概率分布高峰主要集中在区域1和区域2。而位于区域3和区域4的边缘点和噪声点的灰度绝对差较大,在图像中所占比例较小。
3.2 阈值选择
利用新的二维直立图和对称卡方散度设计改进的二维最小卡方散度阈值选择方法。
令原始图像F离散概率分布为:
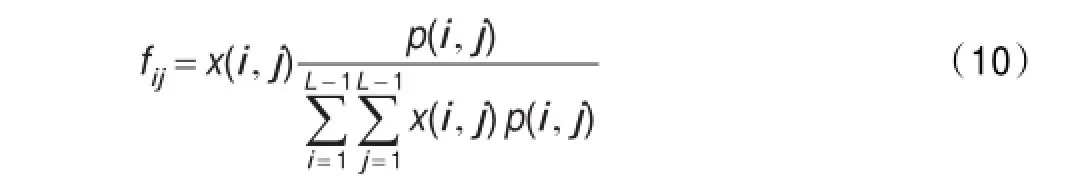
分割后图像G的离散概率分布为:
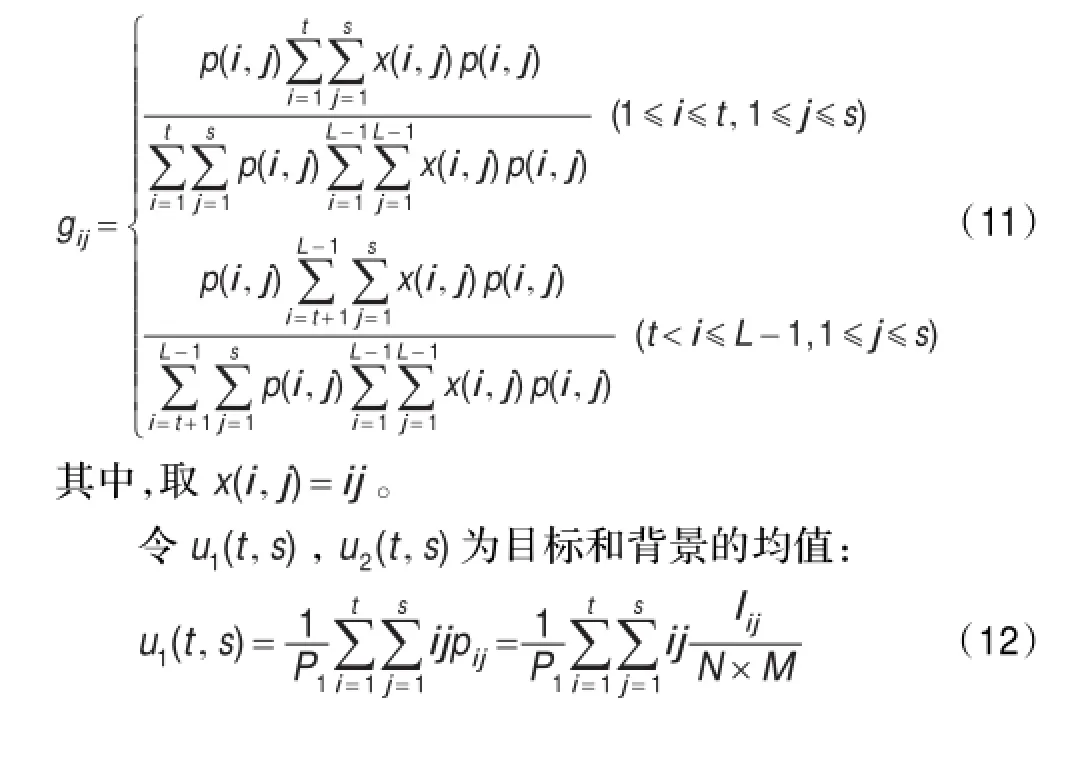


为了提高抗噪性效果,本文采用了关键阈值分割,即在进行分割时阈值向量中起决定作用的那个分量,依据式(20),就是阈值向量的差。然后用此阈值对邻域图像,即滤波后的图像进行分割:

4 仿真实验与分析
实验选取文献[5]中的Otsu法和文献[10]中Li和Lee提出的最小交叉熵法结合传统均值二维直方图,构成二维的Otsu和二维最小交叉熵方法,并用这两种方法与本文的方法进行对比实验。实验用计算机是Pentium®CPU2.66 GHz,2 GB内存,编程工具是Matlab7.0。
形象生动的比喻手法能将事物写得更具体,给人留下深刻的印象。如《台湾的蝴蝶谷》中“有的山谷里有几种蝴蝶,上下翻飞,五彩缤纷,就像谁在空中撒了一把把五颜六色的花瓣,随风飘来,又随风飘去。”“一把把五颜六色的花瓣”指的是山谷里“上下翻飞,五彩缤纷”的几种蝴蝶,写出了蝴蝶飘飘悠悠的柔美姿态,加上多种多样的绚丽色彩,这美丽的画面就像电影一样呈现在学生的眼前。
4.1 性能评估
对于图像分割方法性能的评估,目前没有一种绝对有效的客观标准。为了对各方法分割性能作定量分析,本文选用文献[10]中使用的误分类误差(Misclassification Error,ME)作为客观评价标准。定义如下:

其中,Bo、Fo分别表示图像的真实背景及前景,BT、FT分别表示分割图像的背景及前景,|·|表示集合·的势。
为了测试各方法性能,首先在一幅合成图像上对各方法进行对比。图2(a)列出的是该合成图像的原始图像,该图像前景由汉字“国”字构成,其像素灰度级为60,背景灰度级为200,图像大小为170×170。图2(b)为原始图像的真实分割图。图2(c)~(e)列出了原始图像分别叠加了密度为0.1的椒盐噪声和均值为0,方差为0.01的高斯噪声以及同时含有以上两种噪声的噪声图像。图2(f)~(h)为几种二维分割方法对图2(c)处理的结果。图2(i)~(k)是对图2(d)处理的结果,图2(l)~(n)是对图2(e)处理的结果。

图2 合成噪声图像的二维直方图法阈值结果
从图2的实验结果可以看出,用本文方法得到的结果清晰地把目标“国”字分离出来了,且残留的噪声点也较少。可见本文方法分割结果是几种二维方法中最好的。
表1列出的是图2中不同分割方法对几种噪声图像进行分割时获得的最佳阈值、误分类误差及运行时间。

表1 噪声图像二维分割结果
由式(24)可知,ME值越小,算法的分割性能应该越好。从图2和表1的结果可看出,不管对于单一噪声还是混合噪声,本文的方法都可以获得比其他方法明显更小的分割误差。又由于卡方散度本身计算过程相对简单,因此本文方法也是以上各组实验中用时最少的一种。

图3 混合噪声图像分割的ME与时间
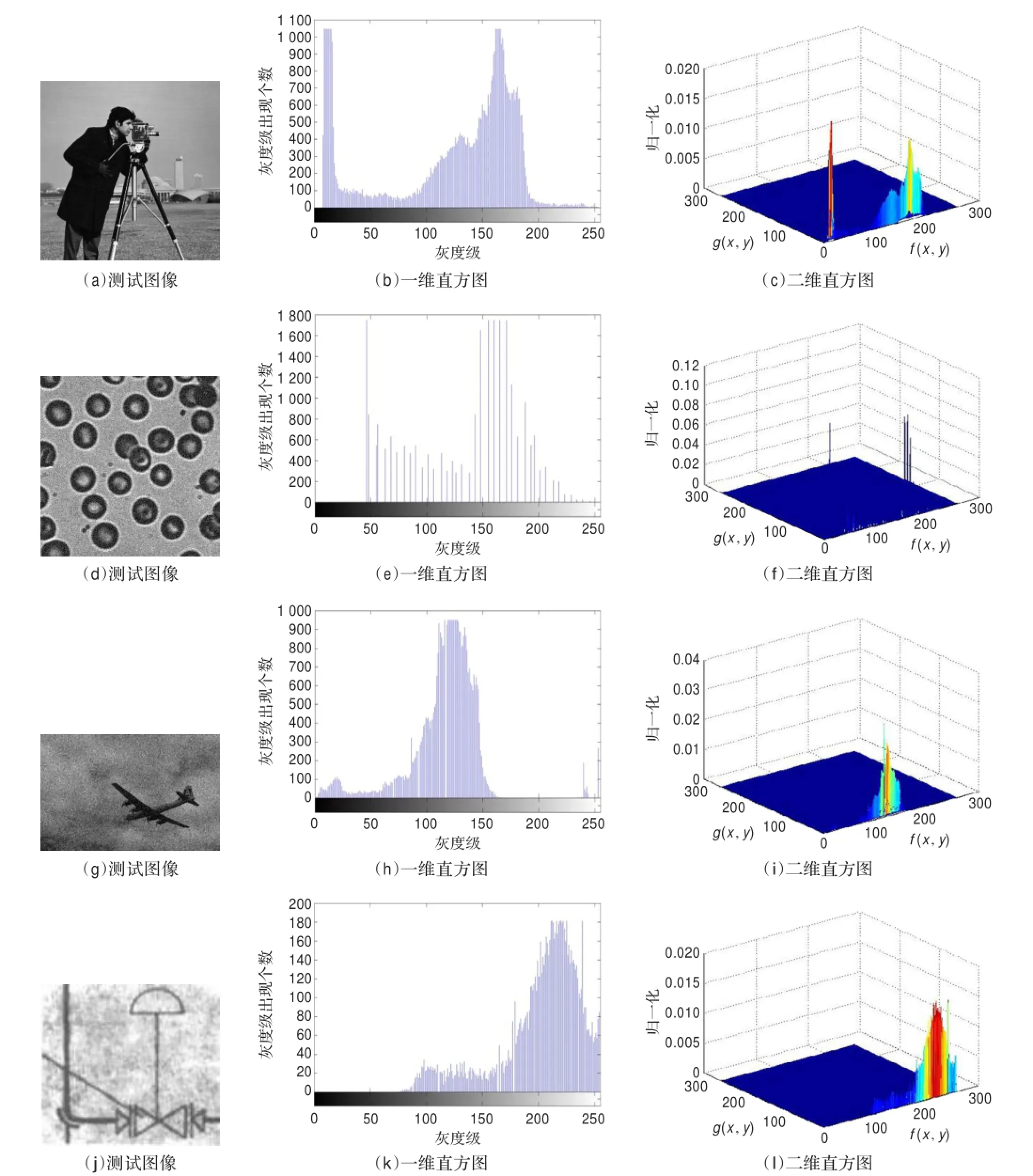
图4 测试图像与其直方图
由图3可知,在处理混合噪声图像时,本文的方法不管在误分类误差还是运行时间上都明显优于二维Otsu法和交叉熵法。
4.2 真实图像上的实验
为了验证本文方法在真实图像上的有效性,在大量对比实验的基础上,本文选取四幅具有不同直方图特点的图像。图4列出了这些原始测试图像及其相应的一维直方图和二维直方图。不同二维方法的图像分割结果如图5所示。
表2和表3列出了几种方法对这四幅不同类型测试图像进行分割时的运行时间和获得的分类误差。

图5 不同二维方法的图像分割结果
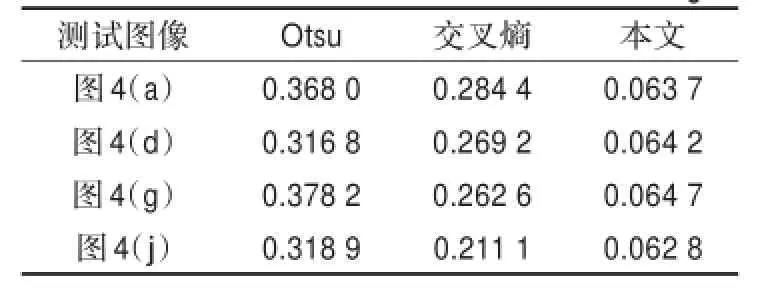
表2 测试图像分割算法的处理时间s

表3 测试图像分割结果的误分类误差(ME)
由以上结果来看,对不同直方图特点的测试图像,基于改进卡方散度在运行时间和分割误差方面都比Otsu和交叉熵阈值法都有所改善。
5 结束语
本文提出了一种改进的卡方散度图像阈值化分割方法。在该方法中,通过对称卡方散度公式并利用新的二维直方图设计了一种适合图像阈值化问题的准则函数,最后用关键阈值对滤波图像进行阈值分割。与现有的阈值化方法相比,在合成图像的仿真实验中,得到的误分类误差指标说明了提出方法的优越性,本文方法能够得到更好的分割结果。在真实图像上的实验也表明方法对纷繁复杂的图像进行阈值化时具有更好的适应性。值得提出的是,本文方法还大大提高了算法的处理所需时间。然而作为交叉熵的外延处理方法,并没有研究它在处理图像系统时的非广延性。因此,对算法的进一步优化也是下一步需要做的工作。
[1]Gonzalez R C,Woods R E.数字图像处理[M].阮秋琦,阮宇智,译.2版.北京:电子工业出版社,2003.
[2]Weszka J S.A survey of threshold selection techniques[J]. Computer Graphics and Image Processing,1978,7(2):259-265.
[3]Sahoo P K,Soltani S,Wong A K C,et al.A survey of thresholding techniques[J].Computer Vision,Graphics,and Image Processing,1988,41(2):233-260.
[4]Sezgin M,Sanakur B.Survey over image thresholding techniques and quantitative performance evaluation[J].Journal of Electronic Imaging,2004,13(1):146-165.
[5]Otsu N.A threshold seclection method from gray-level histograms[J].IEEE Transactions on Systems,Man and Cybernetics,1979,9(1):62-66.
[6]Kittler J,Illingworth J.Minimum error thresholding[J].Pattern Recognition,1986,19(1):41-47.
[7]Pun T.A new method for grey-level picture thresholding using the entropy of the histogram[J].Signal Processing,1980,2(3):223-237.
[8]Kapur J N,Sahoo P K,Wong A K C.A new method for gray-level picture thresholding using the entropy of the histogram[J].Computer Vision,Graphics and Image Processing,1985,29(3):273-285.
[9]Wong A K C,Sahoo P K.A gray-level threshold selection method based on maximum entropy principle[J].IEEE Transactions on Systems,Man,and Cybernetics,1989,19(4):866-871.
[10]Li C H,Lee C K.Minimum cross entropy thresholding[J]. Pattern Recognition,1993,26(4):617-625.
[11]Li C H,Tam P K S.An iterative algorithm for minimum cross entropy thresholding[J].Pattern Recognition Letters,1998,19(8):771-776.
[12]Brink A D,Pendock N E.Minimum cross-entropy threshold selection[J].Pattern Recognition,1996,29(1):179-188.
[13]Pearson K.On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling[J].Phil Mag,1900,50:157-172.
[14]乔韡韡,吴成茂.基于卡方散度阈值方法的图像分割研究与实现[J].计算机应用与软件,2008,25(10):78-81.
[15]唐英干,邸秋艳,赵立兴,等.基于二维最小Tsallis交叉熵的图像阈值分割方法[J].物理学报,2009,58(1):10-14.
[16]张恒,雷志辉,丁晓华.一种改进的中值滤波算法[J].中国图象图形学报,2004,9(4):409-411.
WANG Chen1,2,FAN Yangyu1,XIONG Lei2
1.School of Electronics&Information,Northwestern Polytechnical University,Xi’an 710072,China
2.School of Aeronautics and Astronautics Engineering,Air Force Engineering University,Xi’an 710038,China
Traditional cross-entropy thresholding method is sensitive to noise and with much longer computation time.In order to improve the performance of this algorithm,a novel image thresholding segmentation criteria based on 2-D minimum chi-square divergence is proposed.A novel 2-D histogram based on improved median filter is structured.The difference between the segmented image and the original one is measured by the symmetric chi-square divergence.The neighborhood image is segmented with the key threshold to obtain better segmentation effects.Experimental results demonstrate that the proposed method’s computing time is much less,and its segmentation effect and anti-noise are better than 2-D minimum cross entropy and 2-D Otsu.
image segmentation;thresholding method;cross entropy;chi-square divergence;key threshold
传统的交叉熵阈值法具有抗噪性能差,计算时间长等问题。为了改进算法的性能,提出了一种二维最小卡方散度图像阈值化分割新准则,构建了基于改进中值滤波的新型二维直方图。利用对称卡方散度描述分割前后图像之间的差异程度。使用关键阈值对滤波图像进行分割,达到最佳的分割效果。实验结果表明,与二维Otsu和二维最小交叉熵法相比,提出的方法不仅大大缩短了分割时间,而且分割性能与抗噪性能更强。
图像分割;阈值法;交叉熵;卡方散度;关键阈值
A
TP391
10.3778/j.issn.1002-8331.1310-0221
WANG Chen,FAN Yangyu,XIONG Lei.Improved image segmentation based on 2-D minimum chi-square-divergence.Computer Engineering and Applications,2014,50(18):8-13.
国家自然科学基金(No.61379104)。
王晨(1977—),女,博士研究生,讲师,主要研究领域:图像分割、特征检测;樊养余(1960—),男,博士(后),教授,博导,主要研究领域:数字图像处理、信号处理、虚拟现实技术;熊磊(1976—),男,博士,副教授,主要研究领域:数字图像处理、模式识别。E-mail:wwangchen77@163.com
2013-10-21
2014-03-10
1002-8331(2014)18-0008-06
CNKI网络优先出版:2014-04-01,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1310-0221.html
