某类解析函数子类的Fekete-Szegö不等式

郭栋，李宗涛，许庆兵

（1.滁州职业技术学院基础部，安徽滁州239000；2.广州民航职业技术学院基础部，广东广州510403）

某类解析函数子类的Fekete-Szegö不等式

郭栋1，李宗涛2，许庆兵1

（1.滁州职业技术学院基础部，安徽滁州239000；2.广州民航职业技术学院基础部，广东广州510403）

利用正实部函数的Fekete-Szegö不等式，对D(λ，α，β)函数类上的系数泛函作了精确估计，在此基础上得到了利用Hadamard卷积定义的新函数类上的Fekete-Szegö不等式。

单叶函数；D(λ，α，β)函数；Fekete-Szegö不等式；Hadamard卷积

1 引言及预备知识

令H表示形如

设f(z)和g(z)都在U内解析。若存在U内满足|ω(z)|≤|z|的解析函数ω(z)，使得f(z)≡g(ω(z))，则称f(z)从属于g(z)，记作f(z)≺g(z)。

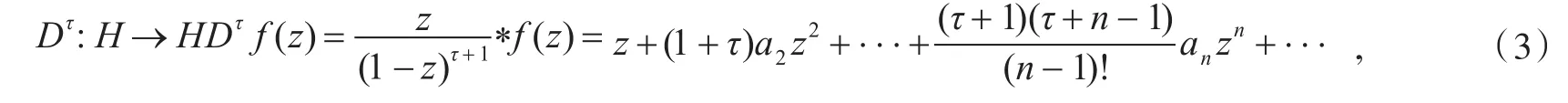
算子Dτ首先由Ruscheweyh研究，也称Ruscheweyh导数。Fekete和Szego¨［5］于1933年证明了如下结果。

定理A设f(z)∈S，f(z)由（1）式给出，则且对每个μ等号都成立。

文献［6-8］研究了H中一些子类的Fekete-Szegö问题。本文研究D(λ，α，β)函数类上的Fekete-Szegö问题，本文中定理1推广了文献［3］中定理［2］的结果，并给出Hadamard卷积在其上的应用。

为了导出文中主要结果，我们需要引用如下引理。

引理1[9]如果内具有正实部的解析函数，则对任意的实数ν，有

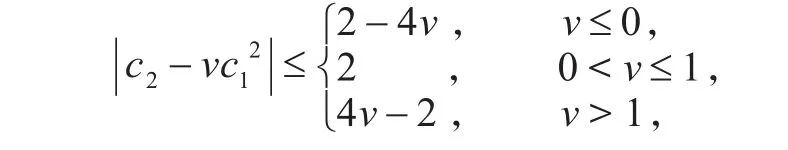
引理中的估计是精确的，ν≤0和ν＞1时，其极值函数为

0＜ν≤1时，其极值函数为

引理2[10]如果内具有正实部的解析函数，则对任意的复数ν，有。等号在函数或者时成立。

2 主要结果及证明

将f(z)，p(z)的幂级数展开式代入（2）式，比较恒等式两边z和z2的系数，可得

定理1的结果是精确的，对所有的μ等号都成立。当μ≤δ1或μ≥δ2时，若λ＞0，对应的极值函数为

若λ=0，对应的极值函数为

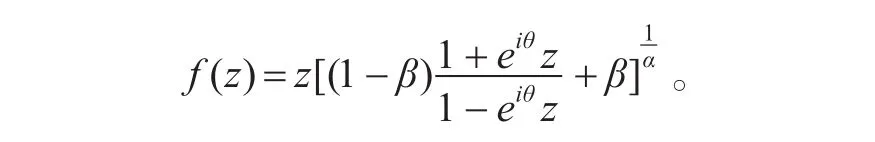
当δ1＜μ＜δ2时，若λ＞0，对应的极值函数为

若λ=0时，对应的极值函数为

注：令α=1时，定理1就是文献［3］中的定理2。

由（5）式及引理2可得下面的定理。

定理2设f(z)∈H由（1）式给出，f(z)∈D(λ，α，β)，μ为复数，则有

且对所有的μ等号都能成立。

定理3设f(z)∈H由（1）式给出，时，则有

其中，δ1=，且对所有的μ等号都能成立。

类似于定理1的证明过程可证定理3。

由（5）式及引理2可得定理4。

定理4设f(z)∈H由（1）式给出，，μ为复数，则有

且对所有的μ等号都能成立。

推论1设f(z)∈H由（1）式给出，Dτf(z)∈D(λ，α，β)，则

（References）

［1］谭立云，张玉林.Bazilevic函数族的一个从属关系及相应极值问题［J］.延安大学学报：自然科学版，1994（4）：7-14.

［3］何维明.某类解析函数的Fekete-Szegö不等式［J］.长沙交通学院学报，1994，10（3）：13-17.

［4］张小平，何建军.一类解析函数的从属关系及其应用［J］.江西科学，2012，30（4）：429-431.

［5］FEKETE M，SZEGÖ G.Eine Bermerkung uberungerade schlichte functionen［J］.J London Math Soc，1933（8）：85-89.

［6］郭栋，李宗涛，杨家稳.一类解析函数类的Fekete-Szego¨问题［J］.华南师范大学学报：自然科学版，2012，44（4）：32-34.

［7］周从会.γ-星函数类的Fekete-Szegö不等式［J］.安徽理工大学学报：自然科学版，2010（2）：75-78.

［8］崔志峰，刘名生.用卷积定义的解析函数子类的Fekete-Szegö不等式［J］.数学杂志，2011，31（5）：954-961.

［9］MA W，MINDA D.A unified treatment of some special classes of univalent functions［C］//Li Z，Ren F，Yang L，et al.Pro⁃ceedings of the conference on complex analysis.Beijing：International Press Inc，1994：157-169.

［10］RAVICHANDRAN V，BOLCAL M，POLATOGLU Y，et al.Certain subclasses of starlike and convex functions of complex orde［rJ］.Hacettepe Journal of Mathematics and Statistics，2005，34：9-15.

（责任编辑：强士端）

Fekete-Szegö Inequalities for Certain Subclasses of Analytic Functions

GUO Dong1，LI Zongtao2,XU Qingbing1
（1.Foundations Department，Chuzhou Vocational and Technical College，Chuzhou 239000，Anhui，China；
2.Foundations Department，Guangzhou Civil Aviation College，Guangzhou 510403，Guangdong，China）

The coefficient of fonctionelleon the class ofD(λ，α，β)functions was accurate⁃ ly estimated，usingFekete-Szegöinequality for the class of real component functions.On this basis，Fekete-Szegöinequalities for the classes of functions defined by Hadamard convolution were obtained.

univalent function；D(λ，α，β)function；Fekete-Szegöinequality；Hadamard convolu⁃tion

O174.51

A

1673-0143（2014）02-0027-04

2013-11-18

安徽省高校自然科学基金项目（KJ2012Z300）

郭栋（1976—），男，讲师，硕士，研究方向：复分析及其应用。