Global Potential Energy Surface for the H+CH4↔H2+CH3Reaction using Neural Networks

Xin Xu,Jun Chen,Dong H.Zhang

State Key Laboratory of Molecular Reaction Dynamics and Center for Theoretical Computational Chemistry,Dalian Institute of Chemical Physics,Chinese Academy of Sciences,Dalian 116023,China

Global Potential Energy Surface for the H+CH4↔H2+CH3Reaction using Neural Networks

Xin Xu†,Jun Chen†,Dong H.Zhang∗

State Key Laboratory of Molecular Reaction Dynamics and Center for Theoretical Computational Chemistry,Dalian Institute of Chemical Physics,Chinese Academy of Sciences,Dalian 116023,China

A global potential energy surface(PES)for the H+CH4↔H2+CH3reaction has been constructed using the neural networks method based on 47783 high level ab initio geometry points.Extensive quasi-classical trajectories and quantum scattering calculations were carried out to check the convergence of the PES.This PES,fully converged with respect to the fitting procedure and the number of ab initio points,has a very small fitting error,and is much faster on evaluation than the modi fi ed Shepard interpolating PES,representing the best available PES for this benchmark polyatomic system.

Potential energy surface,Neural networks,Ab inito,CH5

I.INTRODUCTION

Due to an important role in CH4/O2combustion chemistry[1],H+CH4↔H2+CH3reaction has been extensively studied experimentally and theoretically[2-21].On the other hand,because five of the six atoms involved are hydrogens,the reaction is an ideal system for high quality ab initio calculations of potential energy surface and quantum dynamics studies,and has become a benchmark for developing and testing various theoretical methods for accurate studies of polyatomic chemical reactions[22-37].

Over past decades,substantial efforts have been devoted to constructing accurate potential energy surface (PES)for the title reaction on which dynamics studies can be carried out[38].In 1995,Jordan and Gilbert developed a PES in term of the valence-bond molecular mechanics(VM-MM)type functions[39],which treated the four hydrogen atoms in methane identically [22].The surface,known as the JG PES,together with its various improved versions[23,24],has been widely used to test dynamics methods since then[40-46].

In 2004 Manthe and coworkers constructed the f i rst ab initio based PES by using the Shepard interpolation approach[13,28],on which thermal rate constants for the H+CH4→H2+CH3reaction were calculated with an unprecedented accuracy.However,because the PES only spanned the space region near the transition state, it could not be employed for detailed dynamics calculations.Following that,Bowman and co-workers successively constructed three versions of global PES for this system,namely ZBB1[29],ZBB2 and ZBB3[30], using the permutationally invariant polynomial(PIP) method,based on more than 2×104high level ab initio energies calculated at the RCCSD(T)/aug-cc-pVTZ level of theory[47,48].These surfaces are substantially more accurate than all the preceding surfaces and have produced many interesting dynamics results[29,30].

In 2011 we constructed a version of PES using the modified Shepard interpolation method based on 29999 data points(including energies,f i rst and second order derivatives)obtained from high level ab initio calculations[49].This PES,namely ZFWCZ,was found to be slightly more accurate than ZBB3 PES.Dynamics calculations produced satisfactory agreements between ZFWCZ and ZBB3 surfaces.However,due to the large number of permutation symmetry in the system,the evaluation of PES is very time consuming, making it inapplicable for extensive dynamics calculations.Recently,Welsch and Manthe extended the code of ZFWCZ surface to graphics processing units(GPU) [50].This made the modified Shepard interpolation faster by a factor of 1000 or more.They also presented a revised PES namely ZFWCZ-WM by incorporating more points into the interpolation data set,and recomputing all the energies,gradients and Hessians with RHF-RCCSD(T)method using scaled cc-PVTZ basis set.

In this work,we report a new global potential energy surface for this benchmark system using neural network fitting method based on high level ab initio calculations.Neural networks(NN)are general fitting methods that can be used to fit any shape of function in principle[51].NN method has been applied to fit many high-dimensional PESs for isolated molecules based mainly on density functional theory(DFT)calculations or relatively low level ab initio methods,aswell as for molecule-surface systems based on DFT calculations over the past two decades[52-59].(Two recent comprehensive reviews in literature[60,61]and a new book[62]detailedly describe the development and application of NN method to PES f i tting.)Recently we successfully constructed two very accurate global PESs for OH3and HOCO,using this method[63,64], based on high level ab initio calculations.This not only provided accurate PESs for these two prototypical four atom reactions,but also illustrated clearly that NN is a powerful method to construct accurate ab initio PES for polyatomic systems.As a further improvement,Jiang and Guo proposed the permutation invariant polynomial neural network(PIP-NN)approach,and successfully applied to some 3-atom and 4-atom systems such as H+H2,Cl+H2and OH3,including the symmetric property with respect to the permutation of identical atoms[65-67].

Because there are five hydrogen atoms in CH5system,making it challenging to employ PIP-NN f i tting, we used a smoothed exchange scheme to adapt the permutation symmetry approximately.It is found that the new PES was f i tted more accurately than the previous surfaces,and is much faster on evaluating than the Shepard interpolated PES.Extensive quantum dynamics calculations revealed that this PES is converged respect to the f i tting process as well as the number of ab initio points.

II.METHODS

The feed forward NN with one or two hidden layers was employed to f i t a PES from a large set of molecular conf i gurations.The NN with two hidden layers, denoted as I-J-K-1,has I nodes in the input layer, which equals to the number of bond lengths employed here as input coordinates for a molecular conf i guration, and one nodes in the output layer corresponding to the potential energy value of the input conf i guration.The output of jthneuron in the f i rst hidden layer is

and consequently the fi nal output is given by

where xi(i=1,···,I)are the bond lengths for a molecular con fi guration,the weights wjl,iconnect the ithneuron of(l-1)thlayer and the jthneuron of lthlayer,and the biases bljdetermine the threshold of the jthneuron of lthlayer,f1and f2are transfer functions taken as hyperbolic tangent functions.Similarly,the NN with only one hidden layer was denoted as I-J-1,and has the similar formulation as NN with two hidden layer, just without the output of the second hidden layer.

In this study of the CH5system,the hydrogen atoms are permutated in advance to make the C-H bond lengths form an ascending order.The 15 bond lengths are used for the input layer.The root mean square error (RMSE)which is used to indicate the f i tting quality,is def i ned as

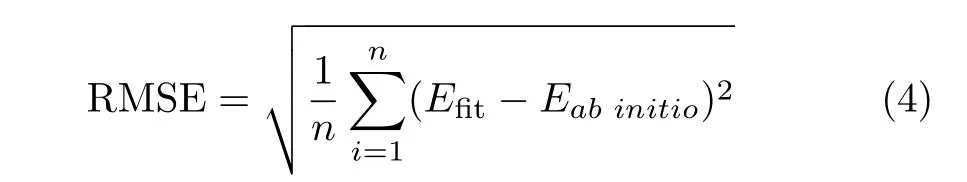
here n is the total number of data points.The neural network parameters,including weights and biases,are optimized using the Levenberg-Marquardt method[68] to reduce the RMSE value.All the data points are divided into training set(90%)and validation set(10%), and the“early-stopping”method[69]is employed to avoid over fitting.

As the case in OH3system,the PES is not exactly continuous at a con fi guration with two or three equal CH bond lengths because the NN functions are not symmetric with respect to the permutation of H atoms,thus may cause problems in quasi-classical trajectory(QCT) calculations.To make the surface suitable for QCT calculations,an average scheme is applied to smooth the PES.In this work,we use 15 inter-atomic distances R to describe the geometry of CH5.For a speci fic geometry,there are 5!=120 di ff erent but equivalent presentations because there are fi ve hydrogen atoms in the system.Firstly,we sort these fi ve hydrogen atoms to have RC-H1≤RC-H2≤RC-H3≤RC-H4≤RC-H5,and defi ne this presentation as R1:

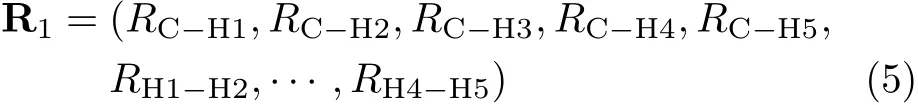
Then the other 119 presentations are generated by permutation of all hydrogen atoms,and def i ned as R2to R120:

Thus,there are 120 neural network outputs noted as V1to V120corresponding to all the arrangements of five H atoms.If the PES was f i tted perfectly,these 120 outputs should be equivalent to each other.But in fact, due to the f i tting error and the non-symmetry propertyof the functional form,these outputs have some differences.We use rito refer to the f i rst 5 terms of each vector Ri:

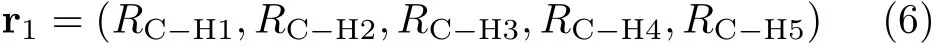
and def i ne a weighting factor wifor each presentation as:

For the f i rst presentation,which has an increasing order of 5 C-H bond distances,the weighting factor w1is the largest,equals to 1.0.For the remaining presentations, the weights are larger if the 5 C-H bond distances are closer to the increasing order.Finally,the PES can be smoothed by multiplying all of these 120 outputs with the corresponding weighting factor wi,and sum them up as:

In order to obtain a global PES covering all the important regions,a complete data set should be selected using a good point selection scheme.Here we use an iterative fitting and adding scheme,originally proposed by Behler[61],and successfully applied to our previous works in construction of OH3and HOCO PESs[63,64]. Firstly,we sample a small set of data points for ab initio calculations,and do NN fittings to these points for several times.Then extensive QCT calculations are carried out to sample the complete geometry space on one of the NN fittings.If a point on a trajectory(a)is located far from the existing points set,or(b)has the fitted energies vary to each other signi ficantly,then this point should be added to the data set and used for further ab initio calculations as well as fitting procedures. This step is repeated iteratively until a converged PES is formed.

III.RESULTS

Ab initio calculations were performed using the F12a amended spin unrestricted coupled cluster method with singles,doubles and perturbative triples based on restricted open shell Hartree-Fock orbitals,together with the augmented correlation-consistent polarized valence triple zeta basis set of Dunning(ROHF-UCCSD(T)-F12a/aug-cc-PVTZ)[70].All the ab initio calculations were carried out with the MOLPRO 2012.1 package [71].

For the existing PESs of CH5system,the ZBB3 PES was f i tted with the permutation invariant polynomialsto 20728 ab initio geometries,and the ZFWCZ PES was constructed using the modi fi ed Shepard interpolation method with 29999 ab initio points.In this work, we fi rst incorporated all the geometries from these two sets,and deleted the duplicated ones using the distance selecting method proposed by Ra ff[54],resulting a total number of～2×104data as the fi rst set of fitting points.Then iteratively,we carried out ab initio calculations for selected geometries,and performed NN fitting of the energies,and ran QCT calculations on one of the fittings to add more data points,as we performed in our previous work[63,64].Eventually a total number of 47783 points were selected to get a converged fitting set.

TABLE I Potential energies and Harmonic frequencies of two transition states obtained from ab initio calculations and the present PES evaluations.

Table I compares the barrier heights as well as harmonic frequencies of the two transition state geometries for abstract reaction and H atoms exchange reaction, calculated by ab initio method and evaluated on PES. The calculated barrier heights(without zero point energy)are 0.636 eV for abstract reaction,and 1.607 eV for H atoms exchange reaction.These two values are well produced by the fitted PES,with error smaller than 0.001 eV.The harmonic frequencies calculated on the fitted PES also agree well with ab initio ones,except that the imaginary frequency of exchange barrier has some discrepancy.

Figure 1 shows the spacial distribution of 47783 ab initio points used in our PES fittings.These data points are evenly distributed over all the spaces.Similar to the OH3PES,we divided the data points into (i):the CH4+H asymptotic part,(ii):the CH5interaction part,and(iii):the CH3+H2asymptotic part,as shown in Fig.1.We used 16835 points for CH4+H part, 20762 points for interaction part and 10186 points for CH3+H2part,respectively.Then we fitted these threeparts and checked the convergence properties separatively to accelerate the NN f i tting procedure and improve the f i tting accuracy.Finally the global PES was obtained by summing the three parts with a weighting factor:

FIG.1 The spacial distribution of ab initio data points as a function of RC-H4and RC-H5,with the dividing lines for the H+CH4,H2+CH3,and CH5interaction parts.

with the switch functions def i ned as

in which logsig is a logistic sigmoid function with the form:

It is straightforward to fit the CH4+H and CH3+H2asymptotic parts accurately by using a NN structure of 15-80-1,to achieve RMSE of 1.96 and 3.18 meV,respectively.Because of the large number of data points and the complexity of the PES in interaction part,the fitting error of this part is～6 meV,slightly larger than the asymptotic parts,with a rather complex NN structure of 15-80-80-1.As in the construction of HOCO PES[64],we also found the use of NN ensembles[72] can make the overall convergence better.We only used the ensembles to construct the CH5interaction part,because the two asymptotic parts have already been fitted accurately.

FIG.2 The maximum,minimum,and average RMSE values of NN ensembles as a function of number of f i ttings contained in an ensemble.

FIG.3 The reaction probabilities of the H+CH4→H2+CH3reaction on NN-1,NN-2,NN-3,and NN-4 PESs obtained by averaging on 4 different sets of f i ttings.

We fitted the interaction part of CH5repeatedly for many times,selected 15 fittings with least RMSEs,and labeled them as Va,Vb,···,Vo.The best fitting has an RMSE value of 5.4 meV and the worst is 6.7 meV,and the mean value of these 15 RMSEs is 6.1 meV.Following that,we selected N number of fittings out of these 15 fittings to form an NN ensemble PES from which we can obtain an averaged PES.For example, for N=5,we can get=3003 di ff erent averaged surfaces.For all the 3003 PES,the minimum RMSE is 3.5 meV,the maximum is 4.0 meV,and the mean value is 3.7 meV.Figure 2 shows the minimum,maximum, and mean RMSEs as a function of the number of fittings in an assembled PES,N.As can be seen the RMSEs decrease steadily with the increase of N,in particular for the fi rst few N,indicating the ensemble method works very well to reduce the fitting error.Considering the calculation e ff ort for QCT calculations will increase linearly using the PES assembled with more fittings,and the overall RMSE decrease slower when N is big,we took N=5 to form an NN ensemble PES in this study.

FIG.4 The reactionprobabilities forthe H+CH4→H2+CH3reaction on the NN-4 PES and NN-5 PES f i tted with 90%of all data points.

Figure 3 compares the total reaction probabilities for the reaction H+CH4→H2+CH3,on these 4 NN ensemble PESs with N=5,in the ground rovibrational state of CH4and the total angular momentum J=0,obtained from the time dependent wave packet method[36,49]. We used Vato Veto form the fi rst ensemble Vabcde, and denoted it as NN-1.Similarly,another two PESs namely NN-2 and NN-3 are generated with averaging Vfghijand Vklmno.In addition,we denoted a PES generated by averaging Vcfklnas NN-4,which has the smallest RMSE value of 3.5 meV among all the 3003 ensembles formed by 5 f i ttings.As can be seen,the reaction probabilities agree to each other very well,indicating the f i tting error of about 4 meV is sufficient small for quantum dynamics calculations,and the f i tting process is well converged for the given data set.By taking the NN-4 PES as the f i nal one for the interaction part and combining it with the two asymptotic parts,we obtained a global PES for CH5with the overall RMSE of 3.0 meV for geometries with ab initio energies less than 1.36 eV respect to H+CH4,and 5.1 meV for energy between 1.36 and 2.72 eV.

To check the convergence of the PES respecting to the number of ab initio points,we randomly deleted 10% points from the set of 47783 geometries,repeated the aforementioned f i tting process to obtain another PES, denoted as NN-5.The dividing scheme and NN ensemble approach were also applied in this PES.Quantum dynamics calculations were carried out on the NN-5 PES to yield total reaction probabilities shown in Fig.4, in comparison with those from NN-4 PES.As seen,the reaction probabilities for the title reaction on these two PESs are almost identical,indicating that the PES is also well converged to the number of ab initio points.

Because the NN functions are not symmetric with respect to the permutation of five hydrogen atoms,we employed a smooth scheme to make the PES suitable for QCT calculations,as described above.In Fig.5,we compare the reaction probability of NN-4 with the unsmoothed version of this PES,namely NN-4u.As seen the smoothed and unsmoothed PESs produced essentially identical quantum dynamics results,as found in OH3system[63].Although the smooth procedure has little e ff ect on quantum dynamics,it can have very important e ff ects on QCT calculations.Unlike the OH3system,the smooth scheme used in NN-4 is computationally demanding because of the high symmetry of fi ve equivalent hydrogen atoms.PIP-NN fitting would be an ideal solution to this problem,but it is very challenging due to the high symmetry for the CH5system. More e ff orts should be put to apply PIP-NN method to this benchmark system.

FIG.5Thereaction probabilitiesfor theH+CH4→H2+CH3reaction on the smoothed NN-4 PES and unsmoothed NN-4u PES.

FIG.6Thereaction probabilitiesfor theH+CH4→H2+CH3reaction on ZBB3,ZFWCZ and the present NN PES.

Figure 6 compares the reaction probabilities for the title reaction on the ZBB3,ZFWCZ,and the present NN PES.As can be seen,the reaction probabilities agree to each other very well in low energy region,in particular on the reaction threshold.The result obtained from this work is close to the ZFWCZ one at the low collision energy below 0.9 eV,while turns to be closer to that from ZBB3 PES at the collision energy of higher than 1.1 eV.Because the NN-4 PES is well converged with respect to ab initio data points and fitting process by extensive quantum dynamics calculations,we believe that the present PES produces the most reliable result.

IV.CONCLUSION

A global PES for the CH5system based on NN fitting to 47783 ab initio energies calculated at UCCSD(T)-F12a/AVTZ level of theory is presented.Using the segmental fitting method[63]and the NN ensembles[72], the overall fitting error can be within 4 meV.The new PES is much faster on evaluating and more accurate on fitting compared with the earlier ZFWCZ PES,representing the best available PES for the CH5system.

Because the NN functions employed in this study are not symmetric with respect to the permutation of H atoms,the energy is not exactly continuous at a confi guration with two or more equal C-H bond lengths, which also occurred in the construction of OH3PES [63].This problem was fi xed by introducing a new averaging scheme,which is generic and can be applied to the F+CH4or Cl+CH4systems,without losing the accuracy of PES fitting.It is better to include the fitting symmetry into the coordinates,just as the PIP-NN method proposed by Jiang and Guo[65,66].However it is not easy to fit the PES of such high symmetry systems like CH5.More work should be done to extend this approach to high dimensional PES with more equivalent atoms,such as CH5and Cl+CH4systems.

V.ACKNOWLEDGEMENTS

This work was supported by the National Natural Science Foundation of China(No.90921014),the Chinese Academy of Sciences,and the Ministry of Science and Technology of China(No.2013CB834601).

[1]J.Warnatz,Rate Coefficients in the C/H/O System, New York:Springer-Verlag,(1955).

[2]M.R.Berlie and D.J.L.Roy,Can.J.Chem.32,650 (1954).

[3]R.Wolfgang,Annu.Rev.Phys.Chem.16,15(1965).

[4]C.C.Chou and F.S.Rowland,J.Phys.Chem.75, 1283(1971).

[5]P.Gray,A.A.Herod,and A.Jones,Chem.Rev.71, 247(1971).

[6]L.M.Raf f,J.Chem.Phys.60,2220(1974).

[7]J.C.Biordi,C.P.Lazzara,and J.F.Papp,Combust. Flame 26,57(1976).

[8]R.K.Boyd,Chem.Rev.77,93(1977).

[9]G.C.Schatz,A.F.Wagner,and T.H.Dunning,J. Phys.Chem.88,221(1984).

[10]M.G.Bryukov,I.R.Slagle,and V.D.Knyazev,J. Phys.Chem.A 105,3107(2001).

[11]F.Fern´andez-Alonso and R.N.Zare,Annu.Rev.Phys. Chem.53,67(2002).

[12]J.P.Camden,H.A.Bechtel,and R.N.Zare,Angew. Chem.Int.Ed.42,5227(2003).

[13]T.Wu,H.J.Werner,and U.Manthe,Science 306,2227 (2004).

[14]J.P.Camden,H.A.Bechtel,B.Ankeny,J.Davida, M.R.Martin,R.N.Zare,W.F.Hu,G.Lendvay,D. Troya,and G.C.Schatz,J.Am.Chem.Soc.127,11898 (2005).

[15]J.P.Camden,H.A.Bechtel,D.J.Brown,and R.N. Zare,J.Chem.Phys.123,134301(2005).

[16]J.P.Camden,H.A.Bechtel,D.J.Ankeny Brown,and R.N.Zare,J.Chem.Phys.124,034311(2006).

[17]Z.Xie and J.M.Bowman,Chem.Phys.Lett.429,355 (2006).

[18]J.P.Camden,W.Hu,H.A.Bechtel,D.J.A.Brown, M.R.Martin,R.N.Zare,G.Lendvay,D.Troya,and G.C.Schatz,J.Phys.Chem.A 110,677(2006).

[19]W.Hu,G.Lendvay,D.Troya,G.C.Schatz,J.P.Camden,H.A.Bechtel,D.J.A.Brown,M.R.Martin,and R.N.Zare,J.Phys.Chem.A 110,3017(2006).

[20]W.Q.Zhang,Y.Zhou,G.R.Wu,Y.P.Lu,H.L.Pan, B.N.Fu,Q.A.Shuai,L.Liu,S.Liu,L.L.Zhang,B. Jiang,D.X.Dai,S.Y.Lee,Z.Xie,B.J.Braams,J.M. Bowman,M.A.Collins,D.H.Zhang,and X.M.Yang, Proc.Natl.Acad.Sci.USA 107,12782(2010).

[21]J.Espinosa-Garc´ıa and J.C.Corchado,Comput. Theor.Chem.1006,123(2013).

[22]M.J.T.Jordan and R.G.Gilbert,J.Chem.Phys.102, 5669(1995).

[23]J.Espinosa-Garc´ıa and J.C.Corchado,J.Chem.Phys. 100,16561(1996).

[24]H.G.Yu,Chem.Phys.Lett.332,538(2000).

[25]J.P.Layfield,M.D.Owens,and D.Troya,J.Chem. Phys.128,194302(2008).

[26]J.C.Corchado,J.L.Bravo,and J.Espinosa-Garc´ıa,J. Chem.Phys.130,184314(2009).

[27]J.Espinosa-Garc´ıa,M.Monge-Palacios,and J.C.Corchado,Adv.Phys.Chem.2012,1(2012).

[28]T.Wu,H.J.Werner,and U.Manthe,J.Chem.Phys. 124,164307(2006).

[29]X.B.Zhang,B.J.Braams,and J.M.Bowman,J. Chem.Phys.124,021104(2006).

[30]Z.Xie,J.M.Bowman,and X.B.Zhang,J.Chem.Phys. 125,133120(2006).

[31]Y.Zhou,C.Wang,and D.H.Zhang,J.Chem.Phys. 135,024313(2011).

[32]R.Liu,H.Xiong,and M.Yang,J.Chem.Phys.137, 174113(2012).

[33]R.Welsch,F.Huarte-Larra˜naga,and U.Manthe,J. Chem.Phys.136,064117(2012).

[34]R.Welsch and U.Manthe,J.Chem.Phys.137,244106 (2012).

[35]R.Wodraszka and U.Manthe,J.Phys.Chem.A 117, 7246(2013).

[36]S.Liu,J.Chen,Z.Zhang,and D.H.Zhang,J.Chem. Phys.138,011101(2013).

[37]Y.Li,Y.V.Suleimanov,J.Li,W.H.Green,and H. Guo,J.Chem.Phys.138,094307(2013).

[38]T.V.Albu,J.Espinosa-Garc´ıa,and D.G.Truhlar, Chem.Rev.107,5101(2007).

[39]T.Joseph,R.Steckler,and D.G.Truhlar,J.Chem. Phys.87,7036(1987).

[40]M.L.Wang,Y.Li,J.Z.H.Zhang,and D.H.Zhang, J.Chem.Phys.113,1802(2000).

[41]F.Huarte-Larra˜naga and U.Manthe,J.Chem.Phys. 113,5115(2000)

[42]F.Huarte-Larra˜naga and U.Manthe,J.Phys.Chem. A 105,2522(2001).

[43]M.Yang,D.H.Zhang,and S.Y.Lee,J.Chem.Phys. 117,9539(2002).

[44]G.Schiffel and U.Manthe,J.Chem.Phys.132,084103 (2010).

[45]G.Schiffel and U.Manthe,J.Chem.Phys.132,191101 (2010).

[46]G.Schiffel and U.Manthe,J.Chem.Phys.133,174124 (2010).

[47]B.J.Braams and J.M.Bowman,Int.Rev.Phys.Chem.28,577(2009).

[48]J.M.Bowman,G.Czako,and B.N.Fu,Phys.Chem. Chem.Phys.13,8094(2011).

[49]Y.Zhou,B.N.Fu,C.R.Wang,M.A.Collins,and D. H.Zhang,J.Chem.Phys.134,064323(2011)

[50]R.Welsch and U.Manthe,J.Chem.Phys.138,164118 (2013).

[51]K.Hornik,M.Stinchcombe,and H.White,Neural Networks 2,359(1989).

[52]T.B.Blank,S.D.Brown,A.W.Calhoun,and D.J. Doren,J.Chem.Phys.103,4129(1995).

[53]D.F.R.Brown,M.N.Gibbs,and D.C.Clary,J.Chem. Phys.105,7597(1996).

[54]L.M.Raf f,M.Malshe,M.Hagan,D.I.Doughan,M. G.Rockley,and R.Komanduri,J.Chem.Phys.122, 084104(2005).

[55]S.Manzhos,X.Wang,R.Dawes,and T.Jr.Carrington, J.Phys.Chem.A 110,5295(2006).

[56]J.Behler and M.Parrinello,Phys.Rev.Lett.98, 146401(2007).

[57]M.G.Darley,C.M.Handley,and P.L.A.Popelier,J. Chem.Theory Comput.4,1435(2008).

[58]H.M.Le,S.Huynh,and L.M.Raf f,J.Chem.Phys. 131,014107/1(2009).

[59]K.V.J.Jose,N.Artrith,and J.Behler,J.Chem.Phys. 136,194111(2012).

[60]C.M.Handley and P.L.A.Popelier,J.Phys.Chem. A 114,3371(2010).

[61]J.Behler,Phys.Chem.Chem.Phys.13,17930(2011).

[62]R.Lionel,K.Ranga,and H.Martin,Neural Networks in Chemical Reaction Dynamics,New York:Oxford University Press,(2012).

[63]J.Chen,X.Xu,X.Xu,and D.H.Zhang,J.Chem. Phys.138,154301(2013).

[64]J.Chen,X.Xu,X.Xu,and D.H.Zhang,J.Chem. Phys.138,221104(2013).

[65]B.Jiang and H.Guo,J.Chem.Phys.139,054112 (2013).

[66]J.Li,B.Jiang,and H.Guo,J.Chem.Phys.139,204103 (2013).

[67]J.Li,J.Chen,D.H.Zhang,and H.Guo,J.Chem. Phys.140,044327(2014).

[68]M.T.Hagan and M.B.Menhaj,IEEE Trans.Neural Netw.5,989(1994).

[69]W.S.Sarle,Proceedings of the 27th Symposium on the Interface of Computing Science and Statistics,Pittsburgh:Interface Foundation of North America,352 (2005).

[70]G.Knizia,T.B.Adler,and H.J.Werner,J.Chem. Phys.130,054104(2009).

[71]H.J.Werner,P.J.Knowles,G.Knizia,F.R.Manby, M.Sch¨utz,P.Celani,T.Korona,R.Lindh,A. Mitrushenkov,G.Rauhut,K.R.Shamasundar,T.B. Adler,R.D.Amos,A.Bernhardsson,A.Berning,D. L.Cooper,M.J.O.Deegan,A.J.Dobbyn,F.Eckert,E.Goll,C.Hampel,A.Hesselmann,G.Hetzer,T. Hrenar,G.Jansen,C.K¨oppl,Y.Liu,A.W.Lloyd,R. A.Mata,A.J.May,S.J.McNicholas,W.Meyer,M. E.Mura,A.Nicklass,D.P.O’Neill,P.Palmieri,D. Peng,K.Pf l¨uger,R.Pitzer,M.Reiher,T.Shiozaki,H. Stoll,A.J.Stone,R.Tarroni,T.Thorsteinsson,and M.Wang,MOLPRO,Version 2012.1,A Package of Ab initio Programs,www.polpro.net,(2012).

[72]D.K.Agraf i otis,W.Cede˜no,and V.S.Lobanov,J. Chem.Inf.Comput.Sci.42,903(2002).

ceived on March 8,2014;Accepted on April 11,2014)

†These authors contributed equally to this work.

∗Author to whom correspondence should be addressed.E-mail：zhangdh@dicp.ac.cn