Molecular Dynamic Simulation of Melting Points of Trans-1,4,5,8-tetranitro-1,4,5,8-tetraazadacalin(TNAD)with Some Propellants
2014-07-19XiaohongLiXuehaiJu
Xiao-hong Li,Xue-hai Ju
a.College of Physics and Engineering,Henan University of Science and Technology,Luoyang 471003, China
b.Department of Chemistry,Nanjing University of Science and Technology,Nanjing 210094,China
Molecular Dynamic Simulation of Melting Points of Trans-1,4,5,8-tetranitro-1,4,5,8-tetraazadacalin(TNAD)with Some Propellants
Xiao-hong Lia,b∗,Xue-hai Jub∗
a.College of Physics and Engineering,Henan University of Science and Technology,Luoyang 471003, China
b.Department of Chemistry,Nanjing University of Science and Technology,Nanjing 210094,China
Molecular dynamic simulation was employed to predict the melting points Tmof TNAD/HMX,TNAD/RDX,TNAD/DINA,andTNAD/DNPsystems(tans-1,4,5,8-tetranitro-1,4,5,8-tetraazadacalin(TNAD),dinitropiperazine(DNP),cyclotetramethylenetetranitroamine(HMX),cyclotrimethylenetrinitramine(RDX),and N-nitrodihydroxyethylaminedinitrate(DINA)).Tmwas determined from the inf l exion point on the curve of mean specific volume vs.temperature.The result shows that the Tmvalues of TNAD/HMX, TNAD/RDX,and TNAD/DINA systems are 500,536,and 488 K,respectively.The TNAD/DNP system has no obvious Tmvalue,which shows the system is insoluble.Using Tm,the solubility of the four systems was analyzed.The radial distribution functions of the four systems were analyzed and the main intermolecular forces between TNAD and other energetic components are short-range interactions.The better the solubility is,the stronger the intermolecular interaction is.In addition,the force field energy at different temperature was also analyzed to predict Tmof the four systems.
Melting point,Molecular dynamic simulation,Radial distribution function, Force field energy,Trans-1,4,5,8-tetranitro-1,4,5,8-tetraazadacalin(TNAD)
I.INTRODUCTION
Nowadays,the search for a kind of new energetic materials with suitable physical properties,performance and sensitivity to meet the future energetic and defense demands has become one of the utmost important regions for chemists and chemical industries.It is also important to f i nd out the physical and thermodynamic properties of these new energetic compounds.The synthesis of energetic compounds is dangerous or not practical,and the measurement for energetic compounds is expensive and time consuming or sometimes even impossible.Theoretical method is a very efficient method for energetic compounds.The calculated properties can help us decide whether it is worth the effort to attempt a new and complex synthesis[1].Some new methods have been recently developed to predict phase transition of different classes of energetic compounds[2-6].
Melting point Tmof a substance is one of the fundamental physical properties in chemical identification, purification and calculation of other important physicochemical properties such as vapor pressure and aqueous solubility.Group additivity methods can be used to predict the melting points of a pure energetic compound by summing the number frequency of each group multiplied by its contribution[7].For a binary system, melting points are not appropriately estimated by the group contribution method[8,9].In addition,research shows that group additivity methods are of questionable accuracy and not reliable procedures to predict melting points[10,11].
Over the last ten years,the molecular dynamics(MD) simulation has been applied to investigate and predict Tm(or glass transition temperature)of amorphous models.Li et al.used MD simulation to compute the glass transition temperature of glycerol-water binary cryoprotectant[12].Tatsumi et al.computed Tmof UO2by MD simulation and the melting point increased with pressure applied to the system[13].
Trans-1,4,5,8-tetranitro-1,4,5,8-tetraazadacalin (TNAD),with the molecular structure of TNAD shown in Fig.1,is an energetic compound containing two nitrous rings,which can be used as a main ingredient in cast explosives and propellants[14-16]. It is characterized as a promising high energy density material(HEDM)with low shock sensitivity and good thermal stability.Recently,Yan et al. studied the compatibility of TNAD with some commonly used energetic materials such as cyclotetramethylenetetranitroamine(HMX),cyclotrimethylenetrinitramine(RDX),dinitropiperazine(DNP),and N-nitrodihydroxyethylaminedinitrate(DINA)by using

FIG.1 The molecular structure of TNAD.
differential scanning calorimetry(DSC)method[17].
Tothebestofourknowledge,thereisstill no report on the prediction of Tmfor the blending amorphous cells of TNAD with energetic components.In the present study,MD calculations were performed to investigate Tmof binary blending system TNAD/HMX,TNAD/RDX,TNAD/DNP, TNAD/DINA.The changes in Tmwere investigated. Using the simulated Tm,the solubilities of the four blending systems were analyzed.Furthermore,radial distribution function and force field energy were also investigated.
II.MODEL CONSTRUCTION AND SIMULATION DETAILS
When a solution is cooled and turned into its glassy state,the heat capacity CP,density,specific volume, radial distribution function,and the formation probability of the H-bonds will show an abrupt change at the melting point.In theory,MD simulation can be used to evaluate the above parameters.For example,Cpcan be expressed as a function of the kinetic and potential energy(k,v),temperature T,pressure P,and volume V of the system during molecular simulation[18],
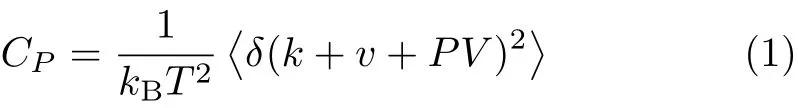
where kBis Boltzmann’s constant.The notation δ(k+v+PV)means(k+v+PV)-〈k+v+PV i,namely energy function,where〈k+v+PV i denotes the equilibrium ensemble average value of quantity(k+v+PV).
Using amorphous cell module of the software Materials Studio[19],four blending amorphous cells were constructed.Each amorphous cell consists of about 1700 atoms.TNAD/HMX cell consists of 28 TNAD molecules and 30 HMX molecules.TNAD/RDX cell has 28 TNAD molecules and 40 RDX molecules,22 TNAD molecules and 40 DNP molecules for TNAD/DNP cell,28 TNAD molecules and 36 DINA molecules for TNAD/DINA cell.The mass ratios of TNAD to HMX, RDX,DNO,and DINA are all 1:1.The initial densities are obtained according to the additivity of volume ratio for TNAD/HMX,TNAD/RDX,TNAD/DNP,and TNAD/DINA blends.Because of conf i gurational diversity,for each pure amorphous cell and each blending amorphous cell,10 different amorphous cells were constructed as the object of the next investigation.
The geometric optimization was performed on the constructed amorphous cells by using Smart Minimization method and COMPASS(condensed-phase optimized molecular potential for atomistic simulation studies)forcefield[20].Using Smart Minimization method, the constructed amorphous molecular models were optimized.In order to make the system cross the potential barrier between the local minima of the potential energy surface,annealing treatment was performed for the amorphous molecular models by the isothermal-isobaric molecular dynamic simulations(NPT-MD)method. The temperature range for the molecular simulation was set from 300 K to 600 K,then from 600 K to 300 K with an interval of 25 K.This process can eliminate the local unreasonable structure produced in constructing amorphous molecular models and provide the more reasonable equilibrium structure for the further MD simulation.
At the stage of cooling from 600 K to 300 K,the NPTMD simulation is performed in the normal pressure and temperature(NPT)with Andersen thermostat method [21]and Berendsen barostat method[22]to control the system pressures and temperatures for the constructed amorphous molecular models.MD simulation cooled to 25 K at each stage,the f i nal equilibrium structure of MD simulation before one phase was taken as the initial structure of the next MD simulation.A f i xed time step of 1 fs was used in all MD simulations.The electrostatic interactions were calculated using the smooth particle mesh Ewald algorithm[23].The average value of the pressure in all simulations was constrained to 1 atm.At each temperature,systems were f i rst relaxed for 50 ps by NVT MD simulation,followed by a production run of 200 ps NPT-MD simulation.The data from the production run were collected.
III.RESULTS AND DISCUSSION
A.Validation of the COMPASS force field
Before carrying out the calculations,we applied twodifferentforcefields,CVFFandCOMPASS (condensed-phase optimized molecular potential for atomistic simulation studies),to the TNAD crystal as a test.The calculated lattice parameters are given in Table I together with the experimental data[24].Obviously,COMPASS forcefield well reproduces the lattice constants of TNAD crystal,which shows that the simulated parameters by COMPASS forcefield are reliable.
B.The melting point of TNAD
In the process of melting phase transition,many physical properties have changed drastically.Up todate,for melting phase transition,no perfect theory can give the correct explanation that is consistent with experiments completely[25].Obviously,volume changes as the temperature changes in melting phase transition. Tmis the temperature at which the volume comes to critical point as it changes from solid to liquid state.So Tmis determined by the inf l ection point on the curve of volume vs.temperature.

TABLE I Comparison of lattice parameter for TNAD crystal with experimental results.

FIG.2 Specific volume of NPT dynamic vs.temperature T for RDX and TNAD.
In order to validate the correctness of the method, Tmof TNAD is predicted by the curve of mean specific volume and temperature,which is obtained by NPTMD simulation from 300 K to 600 K.Two straight lines were obtained by least square f i tting and the intersection of two lines is Tm(Fig.2).From Fig.2,Tmvalue obtained by MD simulation is 510 K for TNAD and the experimental Tmof TNAD is 507 K[26].Obviously,Tmvalue obtained by MD simulation is closer to the experimental Tm,showing that the method to obtain Tmby MD simulation is reliable.
C.Equilibrium criterion
In order to obtain the properties of the constructed systems,the simulation time must be long enough and simulation system must be in equilibrium state.Equilibrium criterion is that the standard deviation of temperature is less than 15 K and energy f l uctuates along a constant value.Figure 3 shows that the prof i les of temperature-simulation time and energy-simulation time of the TNAD/HMX system at 300 K by 200 ps NPT MD simulation.Obviously,the simulation system has achieved an equilibrium state.

FIG.3 Prof i les of temperature-simulation time and energysimulation time of the TNAD/HMX system at 300 K.
D.The melting points of constructed systems
Inthiswork,themeltingpointtemperatures ofTNAD/HMX,TNAD/RDX,TNAD/DNP,and TNAD/DINA blends were predicted by the curve of mean specific volume vs.temperature,which was obtained by NPT-MD simulation from 300 K to 600 K. Two straight lines were obtained by least square f i tting and the intersection of two lines was Tm(Fig.4).From Fig.4,the Tmvalues obtained by MD simulation are 500 K for TNAD/HMX blend,536 K for TNAD/RDX blend,and 488 K for TNAD/DINA blend.But for TNAD/DNP blend,it is noted that there is no obvious inf l ection point,which means that the system has no obvious melting point.
The Tmof the blend can be also used to judge whether the blends are soluble or not[17].When the blends are soluble completely,the system only has one Tmvalue, which is between the Tmvalues of two pure components. If the blends are insoluble completely,the system has no obvious Tmvalue.If the blends are soluble incompletely,the Tmvalues of different components close to each other because of the mutual dif f usion.The better the solubility is,the closer Tmvalue is.
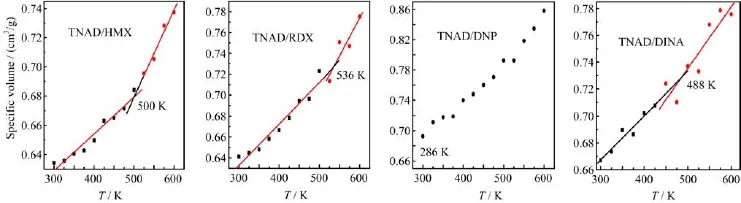
FIG.4 Specific volume of NPT dynamic vs.temperature T for different conf i guration of TNAD/HMX,TNAD/RDX, TNAD/DNP and TNAD/DINA blends.
From Fig.4,it is noted that TNAD/DNP blend has no obvious Tmbecause of the insolubility between TNAD and DNP.For TNAD/DINA and TNAD/RDX blends, the experimental Tmvalues are 493 and 515 K respectively[17],while the Tmvalues obtained by MD simulation are 488 and 536 K respectively,showing that the results by MD simulation are in agreement with the experimental results[17].
It is noted that the Tmof TNAD/DINA blend is higher than that of pure DINA(326 K)[27],but lower than that of pure TNAD(507 K)[26].For TNAD/RDX blend,the Tmof pure TNAD and RDX are 507 K[26]and 479 K[28]respectively,while the Tmof TNAD/RDX blend is 515 K,which is higher than those of pure TAND and RDX.For TNAD/HMX,the introduction of HMX makes the Tmof TNAD/HMX blend come to 500 K,which is lower than those of TNAD (507 K)[26]and HMX(551 K)[27].
E.Radial distribution function
Radial distribution function(RDF)is a characteristic quantity that can ref l ect the microstructure of the materials.It is the probability that,given an atom at the origin of an arbitrary reference frame,there will be an atom with its center located in a spherical shell of inf i nitesimal thickness at a distance r from the reference atom[29].Obviously,the concept embraces the idea that the atom at the origin and the atom at r may be of difference chemical species,A and B.The function of gAB(r)is often used to denote RDF and can be calculated by the average of static relationship of every given pair of particles AB.It is also used to distinguish between amorphous and crystalline structures of the polymers.The def i nition of gAB(r)is as follows:
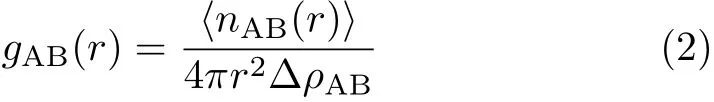
Figure5displaystheRDFsofTNAD/HMX, TNAD/RDX,TNAD/DNP,and TNAD/DINA systems for comparison.In this work,the RDF of TNAD/HMX, TNAD/RDX,TNAD/DNP,and TNAD/DINA systems are analyzed at 298 K.From Fig.5,the higher g(r) appears in the range from 0.3 nm to 1.0 nm,so the main intermolecular forces between TNAD and other energetic components are short-range interactions.In addition,gAB(r)is often used to judge the solubility of blends.If the gAB(r)of the blend is much higher than the gAB(r)of the pure energetic component,the solubility is better.On the contrary, the phase separation may happen[30-32].In this work,r is the distance between the centers of two pure components in blending system,which corresponds to the intermolecular distance of 1.8-2.3˚A.From Fig.5(a),it is noted that the gAB(r)graphs of TNADTNAD and DINA-DINA are closer and they are much lower than that of TNAD-DINA,which shows that TNAD and DINA have the stronger interaction.Consequently,they are soluble.Similar analysis can be made for the gAB(r)graph of TNAD/DINA.For Fig.5(d), the gAB(r)graphs of TNAD-TNAD and DNP-DNP separate clearly and gAB(r)graph of TNAD-DNP is slightly higher than that of DNP-DNP,which shows that TNAD and DNP have not the strong interaction and they are insoluble.By comparison of the gAB(r)graph of the four systems,the order of solubility is TNAD/DINA≈TNAD/RDX>TNAD/HMX>TNAD/DNP,which is consistent with the experimental results[17].
F.Force field energy
According to the principle of molecular mechanics, the total energy in force field is the sum of valence energy,non-bond energy and cross-term interaction energy.Valence energy consists of bond energy,angle energy,and dihedral torsion energy etc.Non-bond energy consists of van der Waals energy and Coulomb interaction energy.Fried et al.thought that there existed the inf l ection points around Tmvalue in the graphs of van der Waals energy versus temperature, dihedral torsion energy versus temperature,non-bond energy versus temperature etc.[33].In order to studythe effect of the force field energy on melting point,the force field energies at different temperatures were analyzed.For TNAD/HMX,TNAD/RDX,TNAD/DNP, and TNAD/DINA,Figs.6-9 plot the graphs of temperature and force field energy such as bond energy, angle energy,dihedral torsion energy,and non-bond energy,respectively.

FIG.5 Intermolecular RDF for TNAD/DINA(a),TNAD/HMX(b),TNAD/RDX(c),and TNAD/DNP(d).
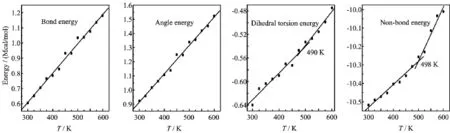
FIG.6 Plots of energy components versus temperature for TNAD/HMX system.
From Figs.6-9,it is noted that the bond energy and angle energy increase with the increment of the temperature for the four systems,which shows that the bond energy and angle energy have no effect on the melting point whatever the four systems are in solid state or liquid state.For the four systems,the angle energy of TNAD/DINA system is the largest,while the angle energy of TNAD/DNP system is the smallest.The angle energy of TNAD/HMX system is larger than that of TNAD/RDX system.
At the same temperature,the dihedral torsion energy of TNAD/RDX system is the largest but that of TNAD/DNP system is the smallest.This is because the attachment of nitro group to DNP makes the steric effect of RDX larger,which results in the increment of dihedral torsion energy of TNAD/RDX system. In addition,it is noted that there exist the inf l ection points in the graph of the dihedral torsion energy versus temperature and non-bond energy versus temperature for TNAD/RDX,TNAD/HMX,and TNAD/DINA systems.The dihedral torsion energy and non-bond energyincrease sharply with the increment of the temperature above Tm,while they increase slowly with the increment of the temperature below Tm.For TNAD/DNP system,there are not obvious inf l ection points in the graph of the dihedral torsion energy versus temperature and non-bond energy versus temperature,which shows that TNAD/DNP system has no obvious Tmand TNAD and DNP are insoluble.
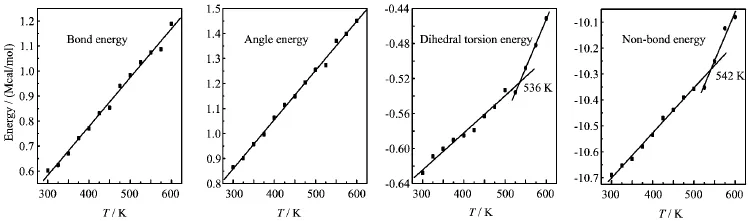
FIG.7 Plots of energy components versus temperature T for TNAD/RDX system.
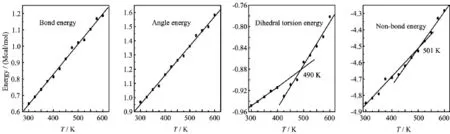
FIG.8 Plots of energy components versus temperature T for TNAD/DINA system.

FIG.9 Plots of energy components versus temperature T for TNAD/DNP system.
Table II lists the melting point temperature obtained by temperature versus specific volume,torsion energy, and non-bond energy,respectively.Obviously,Tmobtained by various methods are very close,which further proves the reliability of the method.
IV.CONCLUSION
In this work,MD method has been used to investigate the melting points Tmof TNAD/HMX,TNAD/RDX, TNAD/DINA,and TNAD/DNP systems.Tmwere sim-ulated by the inf l ection points in the graph of specific volume versus temperature,torsion energy versus temperature,non-bond energy vs.temperature,respectively.The results show that:(i)The Tmvalues obtained by MD simulation are 500 K for TNAD/HMX blend,536 K for TNAD/RDX blend,and 488 K for TNAD/DINA blend.TNAD/DNP system has no obvious Tm.Using Tm,the solubility of the four systems are analyzed.(ii)The main interaction way between TNAD and other energetic components is short-range interaction.The RDF can be used to predict the insolubility of blends.The better the solubility is,the stronger the intermolecular interaction is.(iii)The bond energy and angle energy increase linearly with the increment of the temperature for the four systems.(iv)On the curve of dihedral torsion energy versus temperature and nonbond energy versus temperature,there exist the inf l ection points around Tmfor TNAD/HMX,TNAD/RDX, and TNAD/DINA systems.
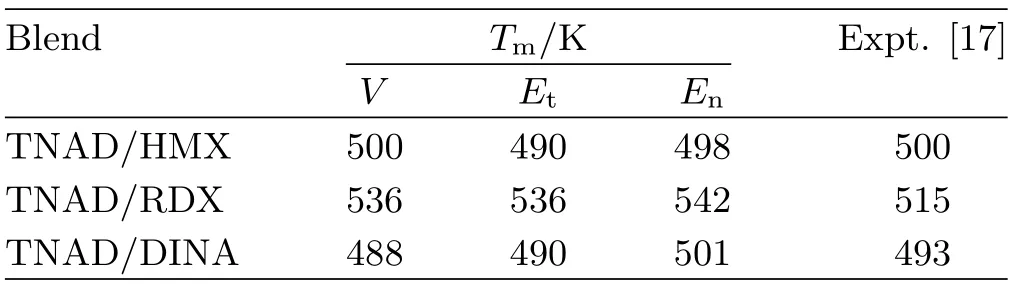
TABLE II The melting point temperature Tmobtained by specific volume V,torsion energy Et,and non-bond energy En,respectively.
V.ACKNOWLEDGMENTS
This work was supported by the National Natural Science Foundation of China(No.U1304111),the Laboratory of Science and Technology on Combustion and Explosion(No.9140C3501021101),China Postdoctoral Science Foundation(No.2013M531361),and Jiangsu Planned Projects for Postdoctoral Research Funds(No.1201015B).
[1]J.P.Agrawal,High Energy Materials:Propellants,Explosives and Pyrotechnics,Weinheim:Wiley-VCH Verlag GmbH&Co.KGaA,102(2010).
[2]M.H.Keshavarz,Important Aspects of Sensitivity of Energetic Compounds:A Simple Novel Approach to Predict Electric Spark Sensitivity,T.J.Janssen,Ed., Explosive Materials:Classification,Composition and Properties,New York:Nova Science Publishers,128 (2010).
[3]M.H.Keshavarz,J.Hazard.Mater.151,499(2008).
[4]M.H.Keshavarz and M.H.Yousef i,J.Hazard.Mater. 152,929(2008).
[5]M.Jaidann,S.Roy,H.Abou-Rachid,and L.Lussier, J.Hazard.Mater.176,165(2010).
[6]M.H.Keshavarz,J.Hazard.Mater.177,648(2010).
[7]Q.Wang,P.Ma,and S.Neng,Chin.J.Chem.Eng.17, 468(2009).
[8]R.C.Reid,J.M.Prausnitz,and B.E.Poling,The Properties of Gases and Liquids,4th Ed.,New York: McGraw-Hill,58(1987).
[9]P.Simamora and S.H.Yalkowsky,Ind.Eng.Chem. Res.33,1405(1994).
[10]E.Poling,J.M.Prausnitz,and J.P.O’Connell,The Properties of Gases and Liquids,5th Ed.,New York: McGraw-Hill,125(2001).
[11]M.H.Keshavarz,J.Hazard.Mater.171,786(2009).
[12]D.X.Li,B.L.Liu,Y.S.Liu,and C.L.Chen,Cryobiology 56,114(2008).
[13]A.Tatsumi,I.Kazuya,I.Yaohiro,T.Yuichi,K.Motoyasu,and Y.Eugene,J.Nuclear Mater.389,149(2009).
[14]C.S.Chang,and T.G.Den,Chemistry 55,89(1997).
[15]H.Ritter and L.Hans-Heinrich,Preparation of trans-1,4,5,8-tetranitro-1,4,5,8-tetraazadecalin by Reaction of Tetraazadecalin with Dinitrogen Pentoxide,Patent DE 19501377 A1,German,(1996).
[16]M.S.Liu,H.J.Tsai,and T.G.Den,Huoyao Jishu 8, 1(1992).
[17]Q.L.Yan,X.J.Li,L.Y.Zhang,J.Z.Li,H.L.Li,and Z.R.Liu,J.Hazard.Mater.160,529(2008).
[18]A.R.Leach,Molecular Modeling-Principles and Applications,2nd Edn.,England:Person Education Limited, 103(2001).
[19]Materials Studio 4.0,Accelrys,Inc.:San Diego,CA, (2006).
[20]H.Sun,J.Phys.Chem.B 102,7338(1998).
[21]H.C.Andersen,J.Chem.Phys.72,2384(1980).
[22]H.J.C.Berendsen,J.P.M.Postma,W.F.Gunsteren, A.Dinola,and J.R.Haak,J.Chem.Phys.81,3684 (1984).
[23]U.Essmann,L.Perera,M.L.Berkowitz,T.Darden, H.Lee,and L.G.Pedersen,J.Chem.Phys.103,8577 (1995).
[24]Q.L.Yan,X.B.Shi,Z.W.Song,H.L.Li,and X.J. Li,Chem.Propel.Poly.Mater.6,30(2008).
[25]P W.Anderson,Science 267,1615(1995).
[26]C.A.Ridgecrest,Trans-1,4,5,8-tetranitro-1,4,5,8-tetraazadecalin,USPatent4443602,C06B25/00, (1982).
[27]J.Z.Li,X.Z.Fan,X.P.Fan,F.Q.Zhao,and R.Z. Hu,J.Therm.Anal.Cal.85,779(2006).
[28]http://webbook.nist.gov/chemistry/
[29]S.SheetalJawalkar,V.S.N.Kothapalli Raju,B.S. Halligudi,S.Malladi,and M.T.Aminabhavi,J.Phys. Chem.B 111,2431(2007).
[30]T.C.Clancy and M.Putz,Macromolecules 33,9452 (2000).
[31]E.D.Akten and W.L.Mattice,Macromolecules 34, 3389(2001).
[32]P.Gestoso and J.Brisson,Polymer 44,2321(2003).
[33]J.R.Fried and P.Ren,Comput.Theor.Poly.Sci.9, 111(1999).
ceived on March 7,2014;Accepted on June 8,2014)
∗Authors to whom correspondence should be addressed.E-mail:lorna639@126.com,xhju@njust.edu.cn,Tel.:+86-379-65626265
杂志排行
CHINESE JOURNAL OF CHEMICAL PHYSICS的其它文章
- Hydrothermal Synthesis and Efficient Visible Light Photocatalytic Properties of InVO4Hierarchical Microspheres and InVO4Nanowires
- Uniform B-C-N Ternary Monolayer from Non-Metal Filled g-C3N4Sheet
- Insights into Elastic and Thermodynamics Properties of Binary Intermetallics in Ni-Al Alloys under Extreme Condition:Full-Electronic Quasi-Harmonic Study
- Negative Differential Resistance of Au-MgB2-Au Nanoscale Junctions
- Effect of Surfactant-Induced Modifications on CuCoMn Catalysts for Higher Alcohol Synthesis
- Composite Cathode based on Mn-doped Perovskite Niobate-Titanate for Efficient Steam Electrolysis
