柴油机冷却水套的优化设计方法*
2014-07-19刘福水闵祥芬李向荣郭良平
刘福水,闵祥芬,樊 丰,李向荣,郭良平
(1.北京理工大学机械与车辆学院,北京 100081; 2.中国人民解放军驻5460厂军代室,石家庄 050081)
前言
随着柴油机强化程度的不断提升,对冷却系统的性能也提出了更高的要求。冷却不足、冷却过度或冷却不均匀都会对柴油机的可靠性和使用寿命造成一定的影响,导致其工作性能下降,严重时甚至不能正常工作[1-3]。
冷却水套内冷却水的三维流动直接影响柴油机的冷却效率、高温零件的热负荷、整机的热量分配和能量利用[4-5]。尤其对高强化多缸柴油机,各缸的冷却均匀性也与上述性能息息相关。因此,在柴油机冷却系统的设计过程中,冷却水套的结构设计是非常重要的环节。
目前,计算流体力学(CFD)已经成为柴油机冷却水套性能研究的重要手段[6-7]。然而,单纯地应用CFD分析的方法对冷却水套进行结构优化,具有优化方向不够明确、工作量大和设计周期长的不足。
本文中将先进的三维计算手段和经典的理论分析方法相结合,提出了一种对水套进行结构优化的有效方法。
采用CFD商用软件STAR-CCM+,对某型六缸柴油机冷却水套进行数值计算,给出了水套缸盖底平面的冷却水速度分布情况,并对各缸冷却水流量均匀性进行了比较分析。针对各缸缸盖冷却水流量分配不均匀的现象进行了理论分析,根据冷却水流量分配和压力损失的关系,引入了流阻图的概念。采用流阻分析的方法,通过改变各缸的上水孔尺寸达到流阻平衡,进而调整各缸盖冷却水的流量分配。基于此方法,对冷却水套进行结构改进,通过改变不同的总进口流量验证了该方法的有效性。
1 冷却水套几何模型的建立
几何形状的准确描述是模拟计算的重要前提。由于柴油机冷却系统结构十分复杂,很难保证建立的计算模型和实体模型完全一致,而且实体模型越复杂,计算所需的时间越长。因此,本文中在保证对数值模拟计算结果不产生很大影响的前提下,对实际的实体结构进行一些简化处理,如不考虑某些过渡圆角、倒角等细节,但对模型的关键位置(如缸盖水套鼻梁区)不作任何简化。
研究对象为开发过程中的某型六缸柴油机冷却水套。图1为该柴油机冷却水套几何模型。
该柴油机采用缸体水套串联式、缸盖水套并联式的冷却水分配形式。即冷却水先从自由端第1缸入水口进入,大部分冷却水依次流入各缸体水套(缸体水套之间由两侧的连通孔连接),同时一部分冷却水通过缸盖上水孔独立进入各气缸缸盖水套,流经缸盖水套后全部汇入回水总管,回水总管出水口也位于自由端。
2 冷却水套计算模型的建立
2.1 计算网格模型
将三维的CAD模型导入到Hypermesh软件中进行面网格划分,选择基本网格尺寸为5mm,并对缸盖鼻梁区、缸体上部等关键流动区域的网格加密。然后将stl格式的面网格模型导入STAR-CCM+中自动生成多面体网格。多面体网格不但可以使计算网格数量大大减少,而且具有计算精度高、收敛速度快等优点。本文中冷却水套模型划分网格总数约为88万。
2.2 计算初始和边界条件
冷却液为纯净水,温度353K下对应的动力黏度为3.551×10-4Pa·s。在数值计算中认为冷却水的流动状态是三维不可压的黏性湍流流动。采用稳态计算模式,利用分离式求解器进行计算,湍流模型选用标准k-ε湍流模型。计算过程中,须求解连续性方程、动量方程、能量守恒方程和湍流模型方程。
入口边界质量流量取7.0kg/s。出口采用压力边界,根据以往的试验数据,表压为0.13MPa。
在计算中采用固定温度边界条件,假定缸盖和缸体平均壁面温度分别为393和373K。由于k-ε模型只适用于离开壁面一定距离的湍流区域,因此对于壁面附近的区域,采用Norris和Reynolds方程低雷诺数模型。
恰当地选择计算初始条件可以加快收敛速度。本次计算中初始值假定:表压为0.13MPa;温度为300K;湍动能为0.01m2/s2;湍动能尺度为1mm;速度为u=v=w=0。
3 CFD计算结果及分析
3.1 速度场分布
由于柴油机缸盖底部,进气门座、排气门座与喷油器之间的鼻梁区热负荷很高,因此应保证缸盖鼻梁区冷却水有良好的流动。由于排气侧的燃气温度较高,因而对排气门附近冷却水流速要求更高。Ricardo公司推荐气缸盖排气门鼻梁区流速为1.0~1.5m/s,进气门鼻梁区的流速为 0.5 ~1.0m/s[8]。
图2为缸盖底平面水流速度分布图。由图可见:排气门鼻梁区比进气门鼻梁区冷却水速度高;缸盖底平面的平均流速为0.95m/s,虽高于工程限值0.5m/s,但局部区域的速度分布还存在一定的差异,尤其第6缸鼻梁区附近冷却水速度偏低。
3.2 缸盖冷却水流量均匀性
针对各缸缸盖底平面速度分布不均匀的现象,对各缸缸盖分配的冷却水流量进行了统计。
定义各缸流量最大不均匀度为
式中:ηi为各缸流量占总流量的比例(i=1,2,…,6)为平均百分比。
图3为各缸盖冷却水流量占总流量的比例。由图可见:各缸盖冷却水流量分配十分不均匀;从第1缸到第6缸,各缸盖分配的冷却水流量逐渐递减,第1缸盖冷却水流量占总流量的25%,第6缸盖仅占12.8%,最大不均匀度达50%。说明大量的冷却水没有在缸体水套内充分流动就通过缸盖水套流出,造成第4、5、6缸冷却水流动性极差。
3.3 压力场分布
图4为冷却水套的压力场分布图。由图可见,总体压力损失为76.5kPa,且压力损失主要发生在缸体和缸盖之间,这主要是由于缸盖上水孔截面突变导致节流作用造成的。
表1为各缸缸盖的压力损失值。由表可见,采用进出口在同一端的方式,容易造成冷却水流经各缸缸盖的流动阻力不平衡,进而造成冷却水流量分配不均匀。因此,在对水套进行结构改进时,要尽量保证冷却水流经各缸缸盖的流动阻力平衡。

表1 各缸缸盖压力损失 kPa
4 冷却水套的结构改进依据
4.1 各缸盖冷却水流量和压力损失的关系
图5为由计算数据拟合形成的各缸缸盖冷却水流量和压力损失的关系曲线。
由图可见,在各缸缸盖上水孔尺寸一样的情况下,各缸盖冷却水流量基本和压力损失的开方成正比,即
式中:Qi为各缸缸盖分配的冷却水流量,kg/s,入口总流量Q=∑Qi;Δpi为各缸缸盖入口和出口间的压力损失,kPa。
式(2)与式(3)节流式流量计的流量公式[9]形式相吻合,验证了计算结果的可靠性。
式中:q为流量;K为流量系数,是与工作介质的黏性和流道几何结构有关的常数;p1、p2为入口截面和出口截面的压力;z1、z2为入口截面和出口截面的高度。
4.2 等效流阻方法的引入
由式(2)可知,若将流经每缸缸体水套、上水孔、缸盖水套和回水管的冷却水流量看作电流,压力损失的开方看作电压,则每一部分可看作电阻,且阻值只和结构有关,即
得到水套内冷却水流动的等效流阻图,如图6所示。
图中:R缸体、R上水孔、R缸盖和 R回水管分别代表缸体、上水孔、缸盖和回水管的流阻。并假设6个缸的缸体、上水孔、缸盖和回水管的流阻都对应相等。
对图6中总入口和总出口之间的6个回路可建立压力损失、流量和流阻的相关方程。
对于任意第i(i=1,2,…6)个回路,均满足如下回路方程:
其中:
根据原模型的模拟计算结果,得到各缸缸盖分配的冷却水流量占总流量的比例,如图3所示。具体数值如下:Q1=0.250Q;Q2=0.186Q;Q3=0.162Q;Q4=0.143Q;Q5=0.131Q;Q6=0.128Q。
对于每个回路,总入口和总出口之间的压力损失Δp是相同的。将上述结果分别代入到回路方程中,可以建立方程组。每两个方程联立求解,均可得到如下关系式:
解算后,取平均值,得
4.3 优化目标和求解过程
若想使各缸的流量分配均匀一致,则必须满足:
在工程中,在达到优化目标的前提下,对冷却水套的结构改动越少越好。因此,本次优化过程,保持第6缸上水孔尺寸不变,则第6缸的流阻也保持不变,即
将优化目标对应的各缸流量比例代入到回路方程中,依次解算则可以得到优化目标对应的各缸流阻值。
优化目标对应的各缸流阻如下:
即第1~6缸的相对流阻依次为 1.822、1.505、1.261、1.100、1.021、1.000。
由此可知,改变上水孔或者缸盖的流阻值均可以达到优化目标,但由于缸盖结构复杂,加工时间长,改变缸盖尺寸会造成人力物力的大量浪费,因此本次结构优化只考虑改变上水孔的尺寸。
为了得到上水孔尺寸变化对流阻变化的影响规律,选取图7所示的模型进行CFD计算。设置进口流量为1.167kg/s,出口压力0.13MPa,得到的计算数据列于表2,并拟合出相对流阻和上水孔直径的关系曲线,见图8。
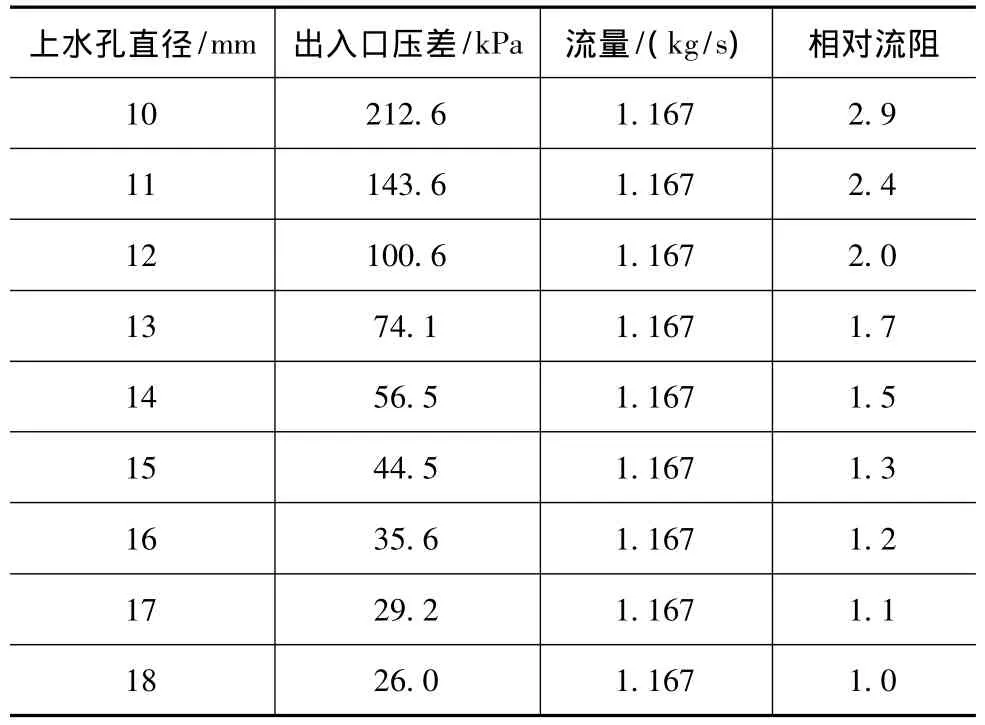
表2 计算数据
由此可以得到优化目标对应的各缸缸盖上水孔直径,如表3所示。

表3 各缸缸盖上水孔直径
5 计算结果分析及改进效果验证
根据表3提供的数据,各缸选用不同直径的上水孔。由于是在原模型的基础上进行结构改进,为了更准确地体现结构改进对冷却性能提高的效果,采用与原模型相同的初始条件和边界条件,启用相同的计算模型。
5.1 改进前后各缸盖冷却均匀性对比
图9为改进前后各缸盖分配的流量占总流量比例的对比图。
由图可见,采用改变各缸的上水孔尺寸达到流阻平衡的方法,对冷却水套进行结构改进后各缸盖冷却水流量最大不均匀度由50%降低到4.6%,各缸盖冷却水流量分配不均匀性得到大幅改善。
5.2 速度场分布
图10为改进前后缸盖底平面速度场分布对比图。由计算结果可知,缸盖底平面的平均流速达到1.01m/s,相对改进前均有一定的提升,且各缸冷却水流速相对更均匀。
图11为改进前后缸盖鼻梁区冷却水平均速度分布对比图。由图可见,与各缸缸盖分配的流量分布相似,改进后各缸鼻梁区冷却水速度分布变得基本均匀。
5.3 压力场分布
图12为改进后的水套整体压力场分布。
由计算结果可知,总体压力损失为99.9kPa。虽然相比改进前有所增大,但现有的水泵仍然可以提供这么大的扬程,因此可通过牺牲一定的压力损失,以达到冷却更均匀的效果。
5.4 不同入口流量下各缸的冷却均匀性验证
改变不同的入口总流量(1.167、2.333、3.500、4.667、5.833和7.000kg/s),分别进行数值计算。图13为不同的总入口流量下,各缸冷却水流量占总流量的比例分布图。由图可见,不同入口流量下的各缸冷却水流量占的比例相差不大,进一步验证了流阻分析方法的有效性。
6 结论
将先进的三维计算手段和经典的理论分析方法相结合,提出了一种对水套进行结构优化的有效方法,可为柴油机冷却水套的优化设计提供方向性指导,得到如下结果:
(1)采用进出口在同一端的方式,容易造成各缸缸盖冷却水流量分配不均匀,必须通过结构优化来保证各缸冷却均匀性;
(2)根据流量和压差的关系,引入了流阻图的概念,采用流阻分析的方法,理论上可以灵活地调整各缸盖的流量分配,从而实现各缸冷却水均匀分布;
(3)采用流阻分析的方法,通过改变上水孔尺寸实现了各缸盖流量分配的均匀性,并通过改变不同的总进口流量验证了该方法的有效性。
[1]蒋德明.高等内燃机原理[M].西安:西安交通大学出版社,2002.
[2]周龙保,刘巽俊,高宗英.内燃机学[M].北京:机械工业出版社,2005.
[3]雷基林,申立中,陈志娥,等.卧式柴油机冷却水套结构优化与流动特性分析[J].农业机械学报,2012,42(11):20.
[4]白敏丽,吕继祖,丁铁心.六缸柴油机冷却系统流动与传热的数值模拟研究[J].内燃机学报,2004,22(6).
[5]Kruger M,Poulsen K M,Mendes A S,et al.Numerical Analysis of Flow at Water Jacket of an Internal Combustion Engine[C].SAE Paper 2008-01-0393.
[6]Siders J A,Tiuey D G.Optimizing Cooling System Performance U-sing Computer Simulation[C].SAE Paper 971802.
[7]Liu Xunjun,Chen Qun,Li Jun,et al.Automotive Diesel Engine Water Jacket CFD Analysis[J].Transactions of CSICE,2003,21(2):125-129.
[8]Ricardo Consulting Engineers Ltd.Ricardo VECTIS CFD Fundamental Theory[M].UK:[s.n.],2005.
[9]罗惕乾.流体力学[M].北京.机械工业出版社,2007.
