混合动力轿车传动系的扭转振动与噪声分析*

邹 良，唐小林，于海生，，张 彤，张建武

(1.上海交通大学机械与动力工程学院，上海 200240; 2.上海华普汽车有限公司，上海 201501)

前言

混合动力车辆(HEV)的动力复合装置一直是各研究机构和厂商的研发重点。行星传动高效可靠、承载力强，在HEV传动系中得到了广泛应用，形成了与激励电机集成的混合动力合成箱技术。相比简单轮系，复合行星轮系结构更复杂、承载更高、传动比更大，随之产生的振动和噪声问题也更严重。建立传动系扭转振动力学模型，揭示其扭振特性，改善噪声、振动和声振粗糙度(Noise、Vibration、Harshness，NVH)，是车辆工程的重要研究课题之一。

文献［1］中的研究表明，当横向支撑刚度与啮合刚度之比大于10时，齿轮系统的纯扭模型相比复杂模型误差较小，实用性较强。文献［2］中对斜齿轮副的耦合振动研究表明，斜齿轮扭转共振和径向共振造成的齿轮动载荷尤为突出，而轴向共振造成的动载荷相对较小。

国内外对简单轮系和多轴斜齿轮副的动力学特性已有很多研究［3－7］，但对复合行星轮系，尤其是结合HEV传动系多输入多输出的实际情况研究较少。本文中以某HEV动力合成箱为研究对象，考虑齿轮副啮合刚度，分析整个传动系的扭转特性，将理论分析与噪声测试结果进行对比，以期为传动系的优化提供参考。

1 动力传动系统描述

某HEV传动系由发动机、扭转减振器、大电机、小电机、复合行星排、二级减速轮、差速器、半轴和车轮等组成，结构如图1所示。

复合行星排前排轮系包括小太阳轮、短行星轮、行星架和齿圈，后排轮系包括大太阳轮、长行星轮以及与前排共用的短行星轮、行星架和齿圈。其轴视图如图2所示。

相比拉维娜结构，该动力合成箱能增大后排轮系杠杆效能，明显降低电机峰值功率要求，进而降低电机的加工制造难度，节约成本［8］。

根据行星排与各动力源的连接方式，可计算得到发动机转速ne和齿圈输出轴转速nr分别为

式中:nls为大太阳轮转速;nss为小太阳轮转速;i1为齿圈与小太阳轮齿数比;i2为齿圈与大太阳轮齿数比。

根据式(1)和式(2)可知，发动机转速与车速相对独立。在车辆行驶过程中，可通过调节大小电机的转速和转矩实现无级变速，同时使发动机始终工作在最优的工作区间。

2 扭转振动模型的建立

2.1 齿轮副啮合刚度的计算

斜齿轮啮合的载荷分布是非均匀的，其弹性变形的计算非常复杂。文献［9］中对大量有限元结果进行回归分析，得到了在轮齿某点作用集中载荷下其他任一点的变形拟合公式。但该方法只用于外齿轮啮合刚度的求解。本文中采用简化公式［10］和石川公式［11－12］计算啮合刚度进行对比研究。通过MATLAB编程计算，得到各齿轮副平均啮合刚度，如表 1 所示。表中 kair、kaib、kais、kbil、krm、kmd分别为短行星轮与齿圈、短行星轮与太阳轮、短行星轮与小太阳轮、长行星轮与大太阳轮、齿圈与减速器齿轮、减速器与差速器的啮合刚度。

表1 齿轮副平均啮合刚度 N·m－1

2.2 齿轮副动力学模型

在不考虑支承轴承和箱体等的弹性变形时，一般圆柱齿轮可等效为扭振动力学模型［13］，见图3。

由图3可推得齿轮副的扭振方程为

式中:J1和J2分别为齿轮1和齿轮2的转动惯量;θ1和θ2分别为齿轮1和齿轮2的角位移;R1和R2分别为齿轮1和齿轮2的基圆半径;T1和T2分别为作用在两个齿轮上的转矩;c为啮合阻尼;k为啮合刚度。

根据其扭振方程，为方便与其他轴系部件连接，齿轮副可等效为两种带有虚拟齿轮的轴系模型，如图4所示。

2.3 复合行星排动力学模型

在不考虑行星架对行星轮支承刚度的情况下，复合行星排的扭振动力学模型［14］如图5所示。设广义坐标 q=［θc，θss，θls，θr，θai，…，θbi］T，规定以逆时针方向转动为正，则无阻尼自由振动时动能与势能之差可表示为

式中:θai、θbi、θc、θss、θls和 θr分别为短行星轮、长行星轮、行星架、小太阳轮、大太阳轮和齿圈的角位移;Jai、Jbi、Jc、Jss、Jls和 Jr分别为短行星轮、长行星轮、行星架、小太阳轮、长行星轮和齿圈的转动惯量;J'c=和 mbi分别为短行星轮和长行星轮的质量;Rai、Rbi、Rss、Rls和 Rr分别为短行星轮、长行星轮、小太阳轮、大太阳轮和齿圈的基圆半径。

根据Lagrange方程从式(4)导出复合行星排的动力学方程组为

式中:M'和K'分别为质量矩阵和刚度矩阵，有

2.4 传动系统整体动力学模型

将齿轮副轴系模型和复合行星排模型整合到传动系中，得到该HEV传动系扭振动力学模型，如图6所示，其中各部件参数如表2所示。

根据图6可推导出各部分的自由扭转振动方程。发动机、减振器和行星架部分扭振方程为

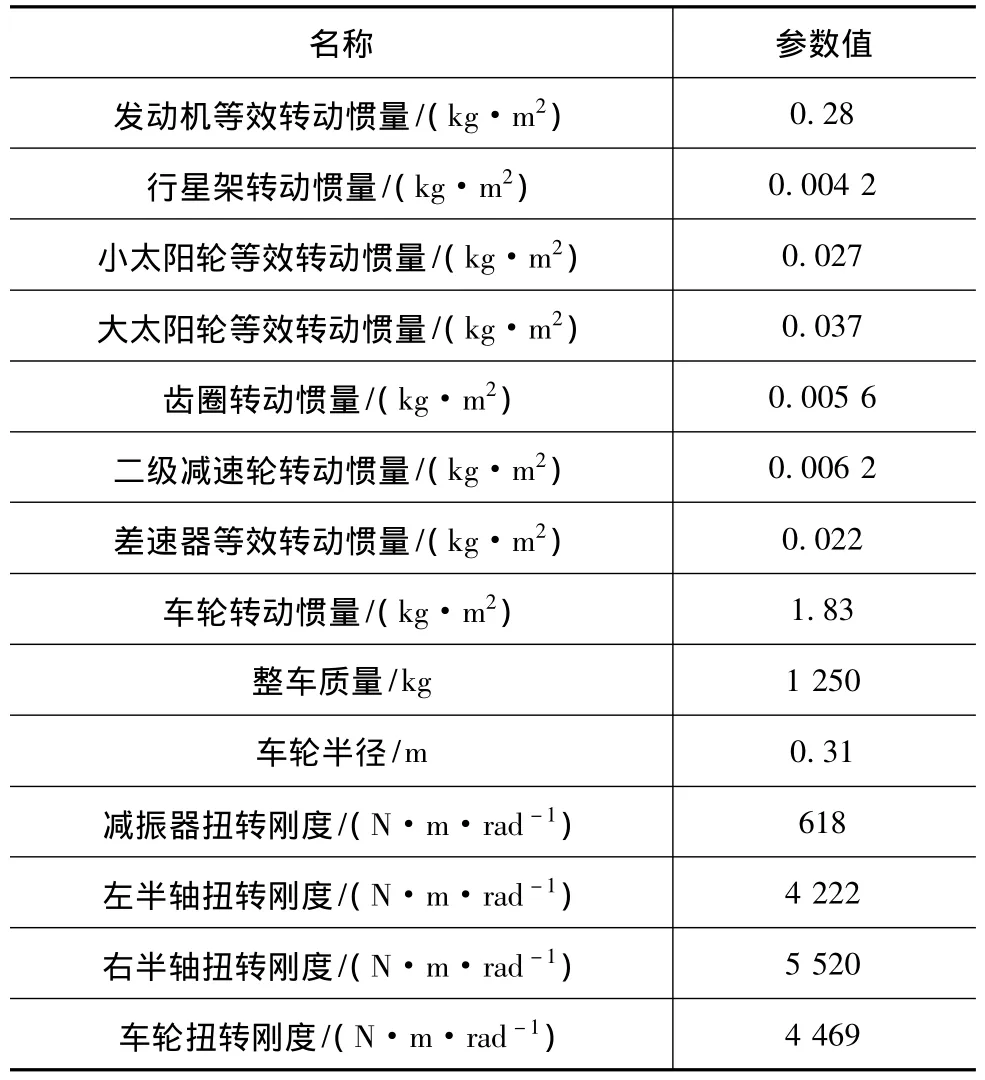
表2 传动系各部件参数

其中:ktc=ktkc/(kt+kc)

式中:kt为减振器刚度;kc为行星架轴扭转刚度;θe为发动机角位移;Je为发动机转动惯量。

齿圈、二级减速轮和差速器的扭振方程为

式中:θm和θd为二级减速轮和差速器的角位移;Jm为二级减速轮转动惯量;krm、kmd为啮合刚度;Rm1、Rm2和Rd为二级减速大、小齿轮和差速器齿轮的基圆半径。

差速器、半轴和车轮部分的扭振方程为

式中:θlt、θrt为左、右车轮角位移;Jd为差速器转动惯量;kla、kra为半轴扭转刚度。

为建立整车与传动系扭振的扭振方程，将整车质量等效到车轮上，通过车轮扭转刚度与传动系连接。故左、右车轮与整车的扭振方程为

式中:Jlt、Jrt分别为左、右车轮转动惯量;ktire为车轮扭转刚度。

整车等效扭振动力学方程为

将式(5)～式(13)整合成系统特征方程为

式中:M为质量矩阵;K为刚度矩阵。

3 传动系扭振特性分析

3.1 固有频率分析

求解式(14)可得传动系的固有频率和模态振型。为提高传动效率和能量利用率，纯电动模式会锁止行星架，混合动力模式会锁止小太阳轮。两种模式在不同刚度计算方法下系统前几阶扭振频率如表3所示。

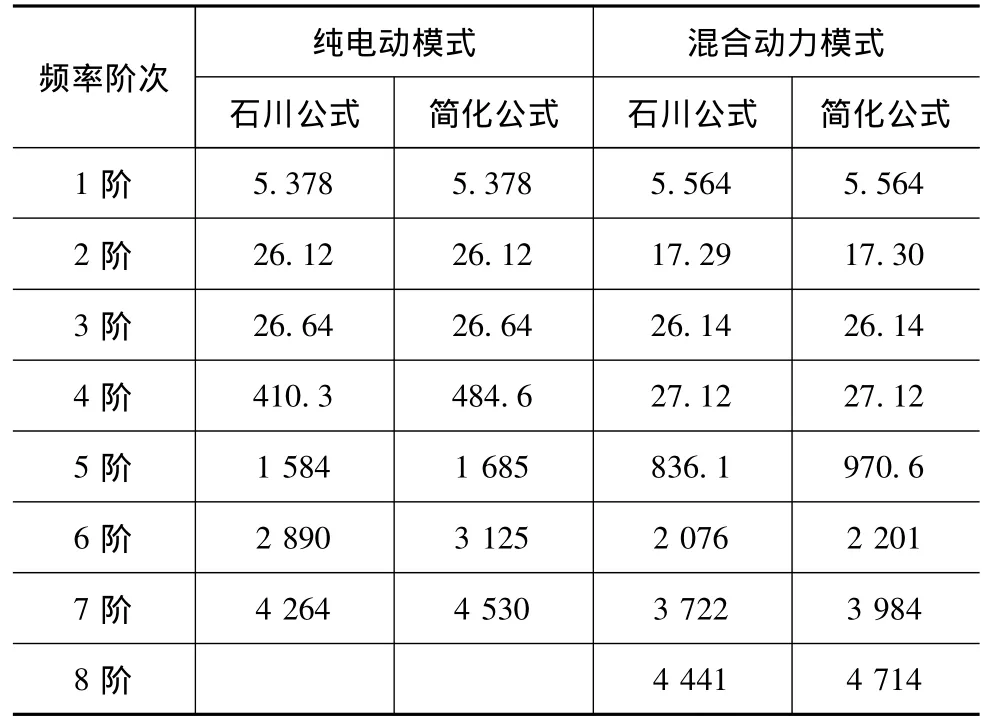
表3 扭转振动固有频率 Hz

3.2 振型分析

将模态振型归一化，去除传动比的影响并整合到同一参考系，得到纯电动模式下传动系各阶模态振型如图7和图8所示，混合动力模式下传动系各阶模态振型如图9和图10所示。

图7和图8中，节点1～14依次代表大太阳轮、3个长行星轮、3个短行星轮、小太阳轮、齿圈、二级减速轮、差速器、左驱动轮、右驱动轮和整车。可以发现，纯电动模式下，1～3阶频率下整车和驱动轮振动明显;4阶频率下大太阳轮的振幅较大，小太阳轮振动也较明显，长短行星轮之间有相对振动;5阶、6阶频率下差速器振幅较大，齿圈和二级减速轮的振幅也较大。

图9和图10中，节点1～15依次为发动机、行星架、大太阳轮、3个长行星轮、3个短行星轮、齿圈、二级减速轮、差速器、左驱动轮、右驱动轮和整车。可以发现，1～4阶频率下整车、驱动轮和发动机的振动明显;5阶、6阶频率下差速器的振幅较大，二级减速轮和行星架的振幅也较大;7阶频率下行星轮振幅较大，差速器和二级减速轮振幅较小。

4 噪声测试与声源辨识

为确定噪声源，对动力合成箱在纯电动和混合动力模式下进行噪声测试。纯电动模式负载电机拉升变化，加速踏板行程30%工况的噪声阶次频谱图如图11所示。混合动力模式下起动工况的噪声阶次频谱图如图12所示。

图11和图12中168阶次对应二级减速轮与齿圈啮合副，298、598阶次对应小太阳轮与短行星轮、大太阳轮与长行星轮、长行星轮与短行星轮、齿圈与短行星轮等啮合副。从图中可识别出，纯电动模式下行星排齿轮啮合是主要噪声源;混合动力模式下发动机噪声较大，行星排齿轮啮合噪声相对较小，但齿圈与二级减速轮啮合噪声仍较强。

噪声测试频率结果如表4和表5所示。

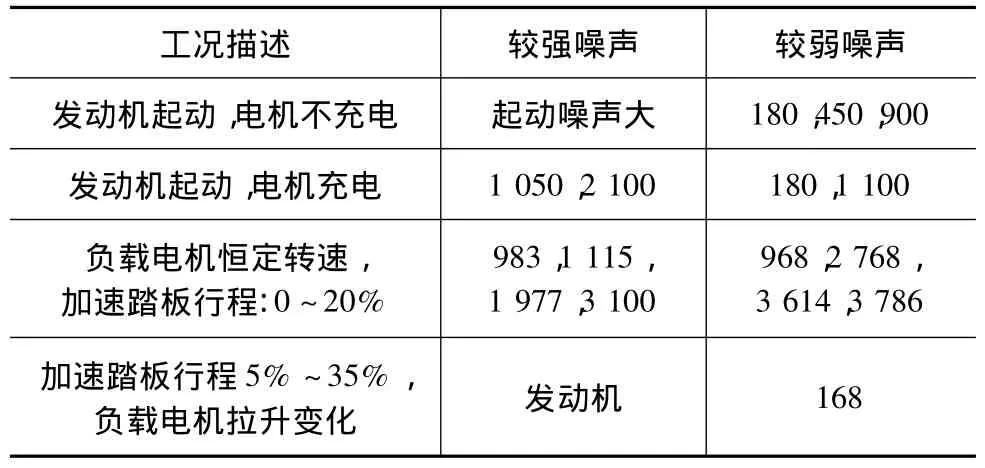
表4 混合动力模式的噪声测试结果 Hz

表5 纯电动模式的噪声测试结果 Hz

由理论分析与测试结果对比可得:纯电动模式下，表3中第4阶频率是太阳轮和行星轮的扭转振动，体现为表5中432～438Hz附近的噪声;表3中第5阶和第6阶频率是差速器、齿圈和二级减速轮的扭转振动，体现为表5中1 630～1 850Hz和3110Hz附近的噪声。混合动力模式下，表3中第5阶和第6阶频率是差速器、二级减速轮和行星架的扭转振动，体现为表4中983和2 100Hz附近的噪声;表3中第7阶频率是长、短行星轮的相对扭转振动，体现为表4中3 786Hz附近的噪声。

5 结论

(1)纯电动模式下，前3阶频率是整车、驱动轮的扭转振动，4～7阶频率为齿轮副的耦合振动;混合动力模式下，前4阶频率下整车、驱动轮和发动机的振幅明显，5～8阶频率下齿轮副耦合振动的同时伴随不同程度的行星架扭转振动。

(2)纯电动模式下，行星排齿轮啮合噪声是主要噪声;混合动力模式下，发动机噪声明显，行星排齿轮啮合噪声相对较小，但齿圈与二级减速轮啮合噪声仍较强。

(3)扭振频率与部分噪声频率相吻合，表明扭转振动对传动系的噪声有重要影响。应采取减小传动误差或增加隔振装置等措施减振降噪，改善行驶平顺性和乘坐舒适性。

［1］Kahraman A.Natural Modes of Planetary Gear Trains［J］.Journal of Sound and Vibration，1994，173(1):125 －130.

［2］陈学东.斜齿圆柱齿轮传动的固有振型特征［J］.武汉工业大学学报，1998，20(1):75 －79.

［3］Eritenel Tugan，Parker R G.Modal Properties of Three-dimensional Helical Planetary Gears［J］.Journal of Sound and Vibration，2009，325(1 －2):398 －406.

［4］Guo Y，Parker R G.Purely Rotational Model and Vibration Modes of Compound Planetary Gears［J］.Mechanism and Machine Theory，2010，45(3):365 －377.

［5］Guo Y，Parker R G.Sensitivity of General Compound Planetary Gear Natural Frequencies and Vibration Modes to Model Parameters［J］.Journal of Vibration and Acoustics，2010，132(1):1 －13.

［6］蔡仲昌，刘辉，项昌乐，等.车辆行星传动系统扭转振动固有特性及灵敏度分析［J］.中国机械工程，2011，22(1):96 －101.

［7］Kubur M，Kahraman A，Zini D M，et al.Dynamic Analysis of a Multi-shaft Helical Gear Transmission by Finite Elements:Model and Experiment［J］.Journal of Vibration and Acoustics，2004，126(3):398－406.

［8］上海华普国润汽车有限公司，浙江吉利控股集团有限公司.双行星排四轴混合动力传动装置:中国，200910194470.5［P］.2011－03－30.

［9］Simon V.Load and Stress Distributions in Spur and Helical Gears［J］.ASME Journal of Mechanisms，Transmissions，and Automation in Design，1988，110:197 －202.

［10］ISO 9085:2002(E)，Calculation of Load Capacity of Spur and Helical Gears-Application for Industrial Gears［S］.2002:47 －50.

［11］日本机械学会.齿轮强度设计资料［M］.李茹贞，赵清慧，译.北京:机械工业出版社，1984.

［12］江荣贵，胡青春.斜齿圆柱齿轮啮合刚度的一种简化计算［J］.机械，2005，32(12):18 －19.

［13］李润芳，王建军.齿轮系统动力学［M］.北京:科学出版社，1997.

［14］Ahmet Kahraman.Free Torsional Vibration Characteristics of Compound Planetary Gear Sets［J］.Mechanism and Machine Theory，2001，36(8):953 －971.