高速车削加工颤振稳定域建模与验证

曹自洋，薛晓红，谢鸥，殷振

(苏州科技学院机械工程学院，江苏苏州215009)

高速车削过程中常常发生切削颤振的动态不稳定现象，其产生源于刀具和工件之间的相互振动，由于上次切削所形成的振纹与当前次切削的振动位移之间的相位差导致刀具切削厚度的不同而引起自激振动，它会导致切屑厚度随着时间变化而变化［1－2］。如果在高速车削中不能够有效地抑制颤振，那么在此工况下加工出的零件会有粗糙的加工面，同时增大刀具的磨损且在切削系统内产生很大的动态载荷。切削系统引发的加工颤振会明显降低切削效率与零件的加工质量，降低刀具、机床的使用寿命，已经成为阻碍该技术发挥其优势的主要瓶颈之一［3－5］。

目前，研究者已经展开了对车削加工颤振的基础研究，试图对颤振进行预测和抑制。BUDAK等［6］通过跨尺度建模对车削的颤振稳定性进行了理论研究。CHEN等［7］通过数值分析研究了无尾架车床的可再生加工颤振，在分析过程中考虑了工件的变形。HAJIKOLAEL等［8］建立了单自由度的车削颤振系统，在建模过程中考虑了车刀后刀面的磨损。KASHYZADEH［9］分别建立了车削系统机床－刀具子系统和刀具－工件子系统的分析模型，对考虑摩擦阻尼的车削加工进行了颤振分析，并通过控制主轴振动来减小振动。上述研究在对车削加工过程建立系统分析模型时，存在研究范围不够宽、软件仿真时的模型过于简单和考虑切削力因素不全面等问题，因而适用性较差，且与实际车削加工过程的差距较大。

此研究针对高速车削加工稳定性问题进行建模和分析，对车削加工过程进行颤振稳定域建模并绘出稳定性叶瓣图，预测车削加工过程的稳定性极限切削宽度，并通过时域仿真得到实际切削点的切削力和刀具法向位移，也通过仿真实验对建立的颤振解析模型进行验证。

1 车削颤振系统动力学建模

车削加工的系统动力学模型如图1所示。由于车削加工的轴向切削力很小，对加工的影响不明显，所以在模型中忽略了轴向力的作用。

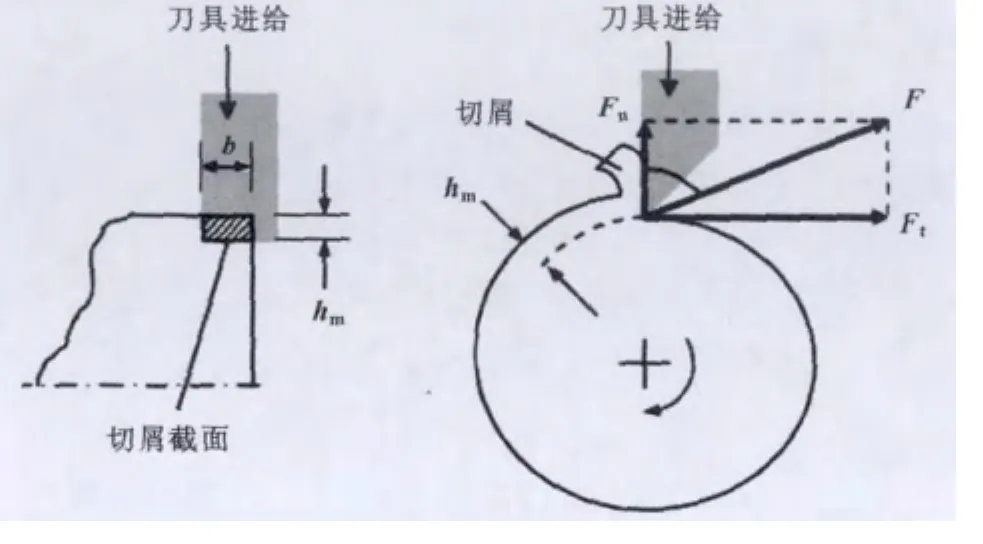
图1 车削加工动力学模型

车削加工过程中的切削力可以表示为切削力系数与切屑面积的乘积:

其中:Fn、Ft分别为总切削力在法向和切向的分量;kn、kt分别为法向和切向的切削力系数;b为切削宽度;h为随时间变化的动态切屑厚度。

再生型颤振主要是由动态切屑厚度的再生效应所致，由于加工表面法向的振动对切屑厚度的影响最大，所以在加工过程中重点考虑加工面法向的振动，可再生的瞬时动态切屑厚度h可表示为:

其中:hm是名义切屑厚度;T是工件旋转一周所需要的时间;y(t－T)是上一次切削的刀具振动量;y(t)是当前次切削的刀具振动量。

从公式 (3)可以看出，动态切屑厚度h取决于名义切削厚度hm和刀具在加工面法向的振动量。如果y(t)＞y(t－T)，那么刀具振动量是逐渐递增的，会导致显著的不稳定切削;如果y(t)=y(t－T)，那么加工过程中的振动量就保持恒定;如果y(t)＜y(t－T)，那么加工过程的振动逐渐衰减，能够获得稳定的切削加工。

把公式 (3)代入公式 (1)，可得到:

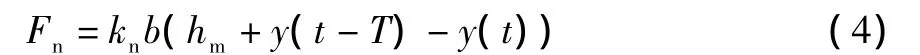
方程 (4)包含了两部分内容，其中定值knbhm并不影响加工系统的稳定性，在分析过程中可以忽略，重点需要分析的是变值knb(y(t－T)－y(t))对加工过程的影响。通过把变值部分的切削力设定为单位力，可以得到:

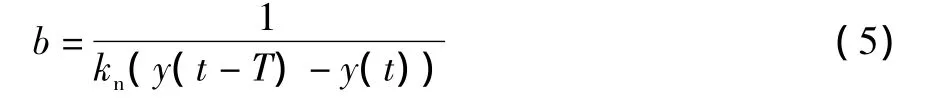
为了找到能够获得稳定加工的极限切削宽度的表达式，在复平面表示出矢量y(t)和y(t－T)，如图2所示。

图2 车刀振动位移的复平面矢量图

其中:ReFRF代表刀具频率响应函数的实部。

从上述分析可以得出，在已知系统动力学参数的情况下，只要得到车削系统的频率响应函数，就可以求出与转速对应的极限切削宽度。

2 车削稳定域加工极限预测

高速车削加工过程的动态特性即车削系统的频率响应函数是分析颤振稳定性的先决条件，现在通常采用结构动态测试或有限元分析两种途径来辨识系统的频响函数。为了符合实际切削加工过程，文中采用模态实验的分析方法，使用冲击力锤激发系统振动，进行结构动态测试，获得车削系统的传递函数，并利用极限切削宽度条件，判别实际加工条件下的切削稳定性。车削实验系统设定的两个方向的系统刚度分别为k1=2.6×107N/m，k2=3.3×107N/m;两个方向的阻尼比分别为ζ1=0.03，ζ2=0.02;实验中设定的名义切屑厚度hm=0.1 mm。通过模态实验的方法获得车削系统的频率响应函数如图3所示。

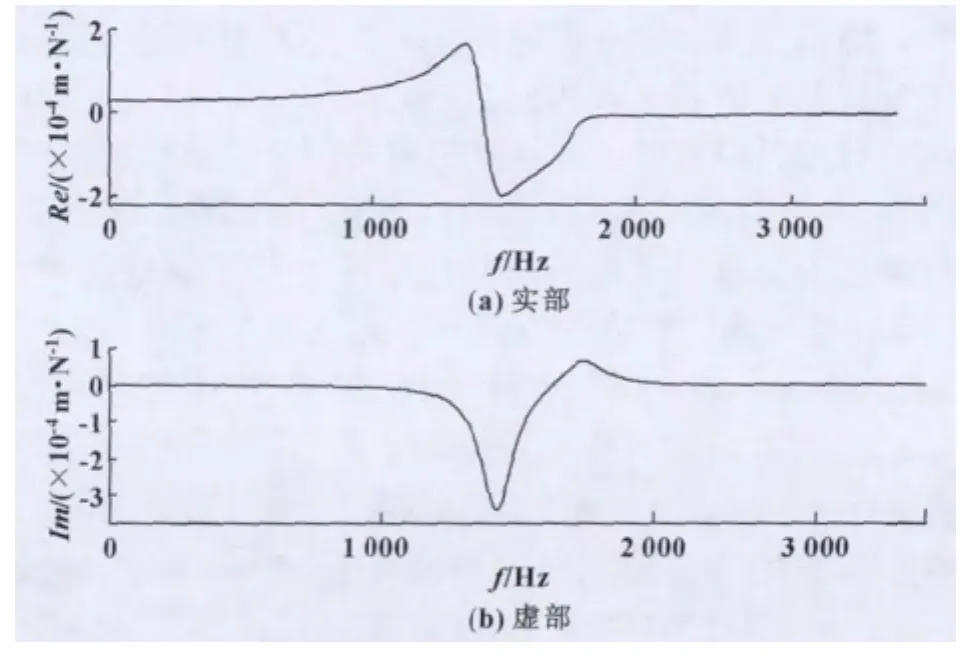
图3 车削实验系统频率响应函数

在切削加工稳定区与非稳定区相交的地方，也就是极限切削发生的位置，此时y=y(t－T)。因为y(t－T)－y(t)代表的是瞬时切屑厚度的变动部分，所以它是一个标量，在图2所示的复平面里面它应该是水平方向的。把y(t－T)－y(t)在复平面的表达代入方程 (5)，就得到极限切削宽度blim的表达式:

在得到系统频率响应函数的基础上，结合公式 (6)，采用 MATLAB软件分析得到叶瓣数N从0到3的车削加工稳定性叶瓣图，如图4所示。其中n为主轴转速，blim为每一个主轴转速下对应的极限切削宽度的大小。

从图4可知:车削加工颤振稳定域由一系列稳定性叶瓣构成，以相邻曲线两两相交的交点隔开，各稳定性叶瓣的波峰从右至左依次降低，波谷保持恒定值。在图线的下方是切削加工稳定区，图线上方为切削加工颤振区。车削加工颤振稳定域叶瓣图直观地给出了稳定切削的加工区间，工艺编制人员可以利用叶瓣图，选择最优的加工参数，避开不稳定切削区域，提高加工效率;或改变原有的切削参数组合，将切削点从不稳定区域转移到稳定区，以避免切削颤振的发生。

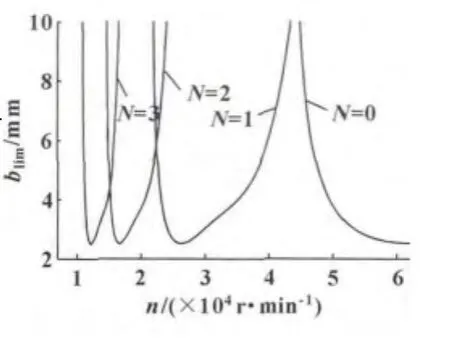
图4 车削加工颤振稳定域叶瓣图

3 时域仿真验证

稳定性叶瓣图能够直观地看出切削加工过程颤振稳定域的全貌，但是对于实际切削点的加工状况，使用稳定性叶瓣图就无法反映，因为它无法表达加工过程的局部状况。为此采用时域仿真的方法找出切削过程中指定加工参数所对应的切削力和刀具法向位移的大小，同时对建立的颤振稳定域进行实验验证。

在图4所示的车削工况中，找出两个有代表性的加工点进行时域仿真。从图4可以看出:实验点1(n=20 000 r/min，b=2 mm)处于加工稳定区，实验点2(n=20 000 r/min，b=4 mm)处于颤振区。对这两组工艺参数对应的工况进行时域仿真，得到点1和点2的切削力、刀具法向位移如图5、图6所示。

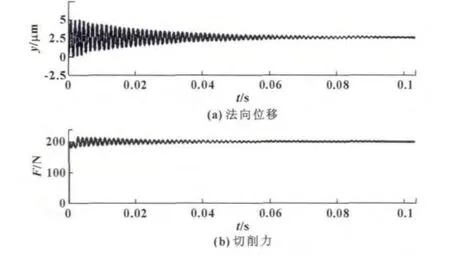
图5 时域仿真得到的切削力和刀具法向位移 (n=20 000 r/min，b=2 mm)

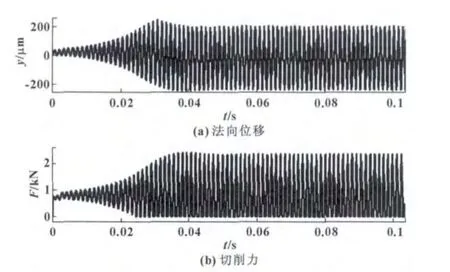
图6 时域仿真得到的切削力和刀具法向位移 (n=20 000 r/min，b=4 mm)

从图5可以看出:处于稳定区的实验点1的切削力恒定，振动信号也非常稳定，刀具振动最大幅值约为5 μm。这种工况切削过程平稳，在实际加工中能够获得较长的刀具寿命和较好的零件加工质量。

同理，从图6可以看出:处于颤振区的实验点2的振动信号的幅值波动很大，刀具位移在加工中瞬间增加到220 μm左右，而且颤振区的切削力也比稳定区的力要大很多。在实际的切削加工中，这种颤振不稳定的工况将会造成刀具严重偏离工件表面，引起刀具的损坏和零件的加工误差。

4 结束语

(1)建立了考虑再生效应的高速车削动态切屑厚度模型和切削力模型。

(2)构建了面向高速车削的颤振稳定域分析模型，采用解析法得到颤振稳定域叶瓣图，预测高速车削的极限切削宽度。

(3)通过车削时域仿真实验得到了加工过程中实际切削点的切削力和刀具动态位移，也验证了建立的车削系统颤振稳定域解析模型的正确性。

［1］CHAE J，PARK S S，FREIHEIT T.Investigation of Microcutting Operations［J］.International Journal of Machine Tools and Manufacture，2006，46:313 －332.

［2］DORNFELD D，MIN S，TAKEUCHI Y.Recent Advances in Mechanical Micromachining［J］.Annals of the CIRP，2006，55:745 －768.

［3］QUINTANA G，CIURANA J.Chatter in Machining Processes:A Review［J］.International Journal of Machine Tools and Manufacture，2011，51:363 －376.

［4］ROSA P，KOLEDNIK O.The Transient Beginning to Machining and the Transition to Steady-state Cutting［J］.International Journal of Machine Tools and Manufacture，2007，47:1904－1915.

［5］INSPERGER T，STEPAN G.State-dependent Delay in Regenerative Turning Processes［J］.Nonlinear Dynamics，2006，47(1):275 －283.

［6］BUDAK E，OZLU E.Analytical Modeling of Chatter Stability in Turning and Boring Operations:A Multi-dimensional Approach［J］.Annals of the CIRP，2007，56(1):401 －404.

［7］CHEN C K，TSAO Y M.A Stability Analysis of Regenerative Chatter in Turning Process without Using Tailstock［J］.International Journal of Advanced Manufacturing Technology，2006，29:648 －654.

［8］HAJIKOLAEL K H，RAHAELFARD M.Spindle Speed Variation for Regenerative Chatter Suppression in Turning Process with Tool Wear Effect［C］//Proceedings of the ASME 2010 10thBiennial Conference on Engineering Systems Design and Analysis，Istanbul，Turkey，2010.

［9］KASHYZADEH K R.Study of Chatter Analysis in Turning Tool and Control Methods:A Review［J］.International Journal of Emerging Technology and Advanced Engineering，2012，2(4):1 －5.