基于神经网络的电液位置伺服疲劳试验机控制系统研究

张彦会，杨丹丹，史维玮，崔传真

(1.广西科技大学广西汽车零部件与整车技术重点实验室，广西柳州545006;2.广西科技大学汽车与交通学院，广西柳州545006)

随着科技的进步，汽车零部件的疲劳测试越来越受到关注，一般的疲劳试验机在稳定性、可靠性等方面已经满足不了现在的测试要求。电液伺服系统由于综合了电子和液压两方面的特点，具有控制精度高、响应快、信号处理灵活、输出功率大、结构紧凑和自重轻等优点，在疲劳试验机的控制上得到了广泛应用。

电液位置伺服系统是疲劳试验机控制系统中的重要组成部分，是典型的机电液耦合系统。其特征主要是非线性、不确定性、时变性等［1］，因此其精确的数学模型不容易建立，在应用传统的PID控制时遇到了很多问题。为了解决电液位置伺服系统控制过程中遇到的问题，文中采用与PID控制相结合的神经网络控制。神经网络系统是大量的神经元互连而成的网络，是在现代脑神经科学研究成果的基础上提出的，反映了人脑功能的基本特征，是人脑的一种抽象、简化和模拟［2］。它具有很强的非线性映射能力，因此在电液伺服控制［3］系统中利用这个特点，将神经网络作为控制器，利用神经网络直接实现对非线性系统的控制［4］。

1 系统的组成

典型的电液位置伺服控制原理框图［5］如图1所示。

图1 电液位置伺服控制原理

此系统主要由伺服放大器、伺服阀、液压缸、位移传感器等组成。计算机向伺服阀发出的控制信号与位移传感器反馈回来的信号进行比较，其差值经伺服放大器处理，以电流的形式控制伺服阀开口，通过伺服阀的流量变化来控制液压缸的位移，实现位置的闭环控制。

伺服阀为零开口四边滑阀，则电液伺服阀的传递函数通常用振荡环节表示为:

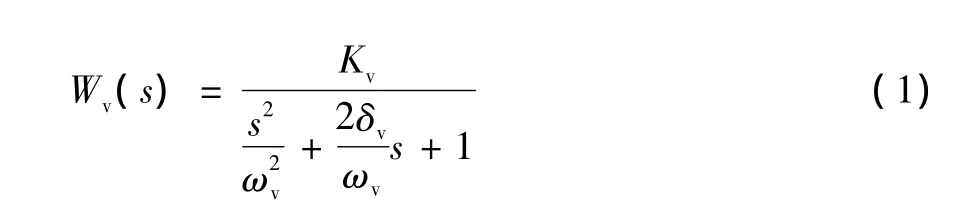
其中:Kv为电液伺服阀流量增益;ωv为伺服阀的固有频率 (rad/s);δv为伺服阀的阻尼比。

2 神经网络PID控制系统设计

神经网络控制主要是为了解决复杂的非线性、不确定、不确知系统在不确定、不确知环境中的控制问题，使控制系统稳定性好、鲁棒性强，具有满意的动静态特性［2］。神经网络控制系统如图2所示，可以看出神经网络控制系统由两部分组成:NNI是辨识器，由于神经网络的学习能力，NNI的参数可随着对象、环境的变化而自适应地改变，所以它可在线辨识不确定、不确知对象的模型;NNC作为控制器，其性能可以随对象、环境的变化而自适应地变化。

图2 神经网络控制系统

神经网络控制系统的工作原理:首先捕获被控对象的输入输出样本对，然后利用NNI对被控制对象进行离线辨识，当辨识的精度达到预定的要求时，通过实时调控NNC的权值系数，使系统达到自适应性，从而实现有效控制的目的［6－7］。

2.1 BP神经网络结构

基于BP神经网络的PID控制器结构图［2］如图3所示，可以看出控制器由两部分组成:

(1)经典的PID控制。直接对被控对象进行闭环控制，并且3个参数kp、ki、kd是在线调整方式。

(2)BP神经网络。输出层神经元的输出状态对应于PID控制器的3个可调参数kp，ki，kd，通过神经网络的自学习、加权系数调整，使神经网络输出对应于某种最优控制律下的PID控制参数。

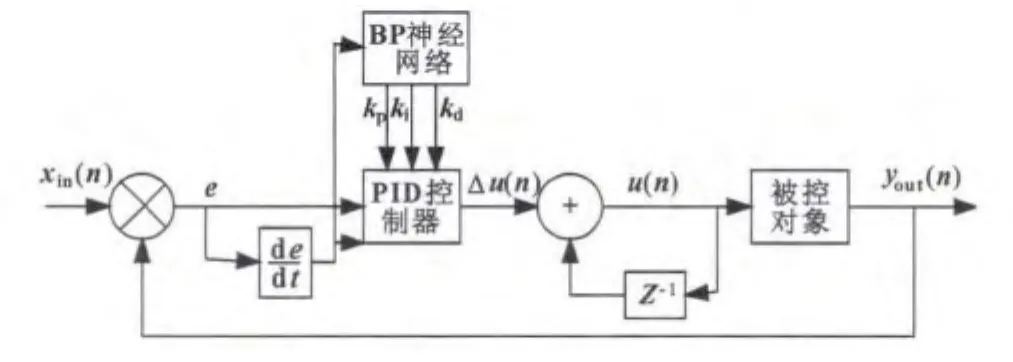
图3 基于BP神经网络的PID控制器结构图

具有隐含层的BP神经网络结构图如图4所示。

从图中可以看出:神经网络辨识器NNI是由3层串并联关系实现的，即输入层、隐含层和输出层。

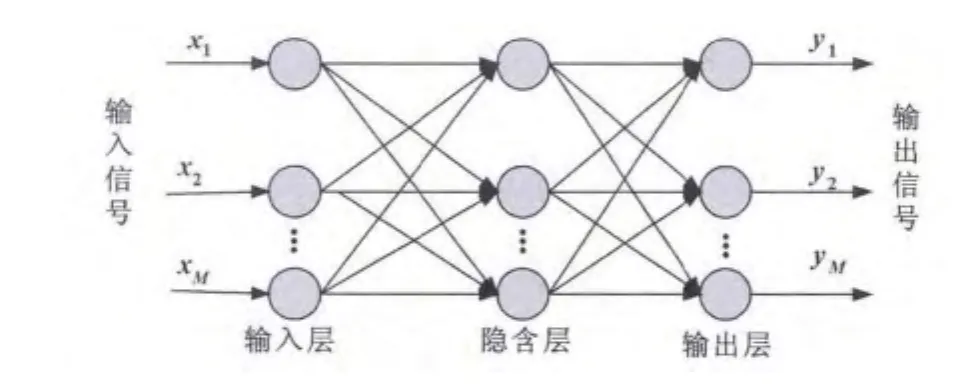
图4 具有隐含层的BP神经网络结构图

2.2 函数信号与误差信号的计算

(1)网络输入层节点的输入输出为

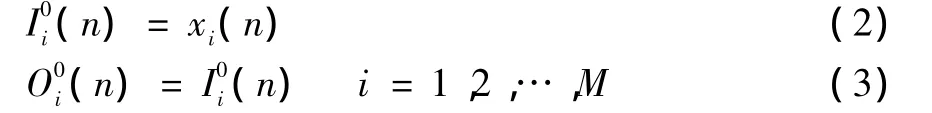
其中:M是输入变量的个数，其值取决于被控系统的复杂程度，此系统中取M=3。变量的右上角标0，1，2分别代表输入层、隐含层和输出层，以下的标注均按此原则。根据以上分析，PID控制器的输入变量分别为:

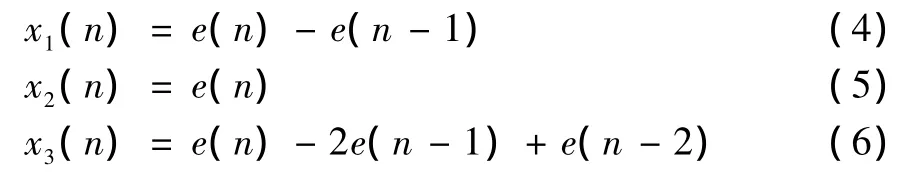
式中:e(n)是控制系统的误差，即e(n)=xin(n)－yout(n)，xin和yout分别是控制系统的期望输出和实际输出。

(2)网络隐含层的诱导局部域和输出分别为

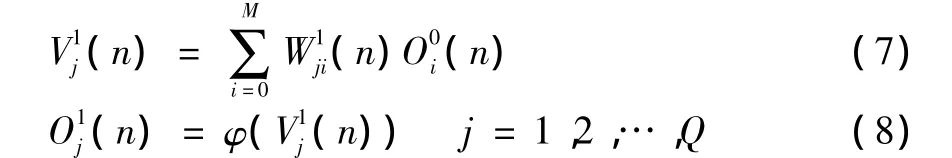
式中:为隐含神经元的加权系数;Q为隐含神经元的节点数。隐含神经元的激活函数取双曲正切函数

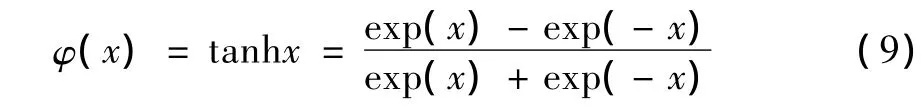
(3)网络输出层的诱导局部域和输出分别为

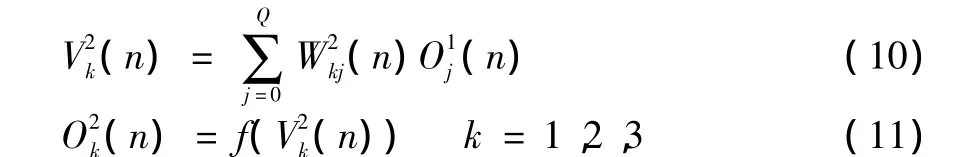
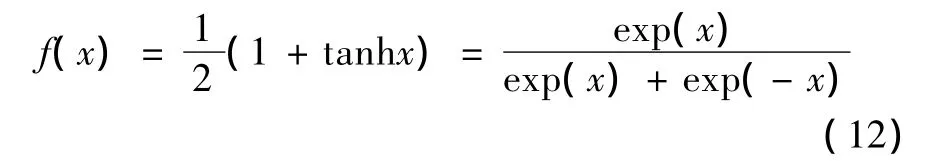
所以PID控制器的控制规律为

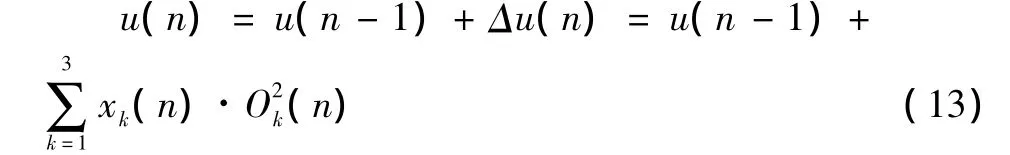
2.3 网络训练算法

系统的性能指标函数为

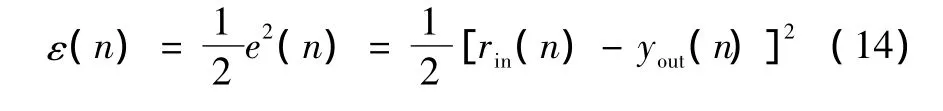
对网络的突触权值进行迭代修正，并附加一个使搜索快速收敛全局极小的动量项

式中:μ是学习率，α是动量因子。

根据微分链式规则，局域梯度可计算如下

将式 (17)代入式 (16)，最后得到神经元的局域梯度为

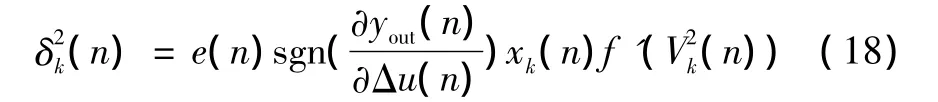
由此可得，网络输出层神经元的突触权值调整的修正公式为

其中:神经元k的局域梯度δ2k(n)可由式(18)确定。

同理，可得隐含层神经元的突触权值学习算法为

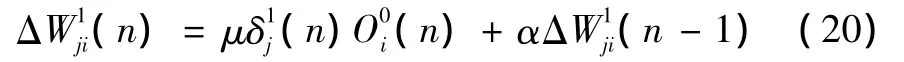
其中:神经元j的局域梯度δ1j(n)为

3 试验验证

疲劳试验台如图5所示，以某乘用车的车桥为试验对象，加载波形以正弦波为例，验证设计的控制系统的效果。

图5 疲劳试验台

利用基于BP神经网络的PID控制算法，得到了系统对输入信号的响应结果。根据系统性能的要求，回路传递函数可近似表示为

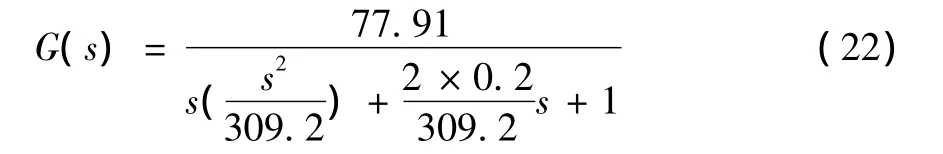
经过实际测试，得到如图6所示的车桥的阶跃响应曲线，图7所示的车桥阶跃跟踪误差曲线。当输入为正弦信号时，得到图8所示的神经网络PID控制的车桥正弦跟踪曲线，图9所示的车桥正弦跟踪误差曲线。

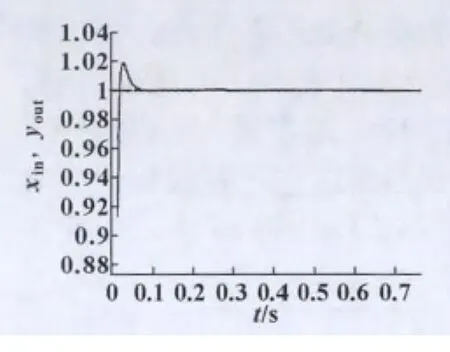
图6 车桥的阶跃响应曲线

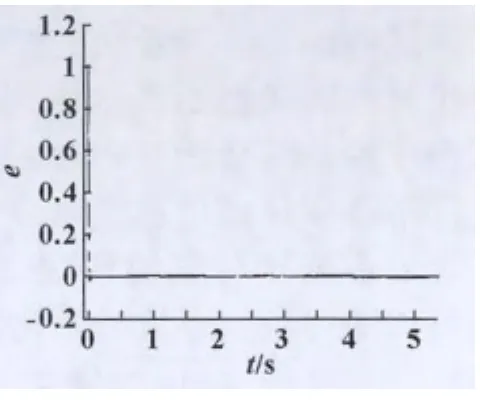
图7 车桥的阶跃跟踪误差曲线

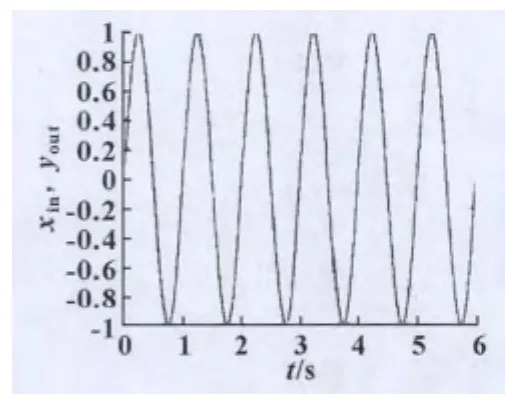
图8 神经网络PID控制车桥正弦跟踪信号

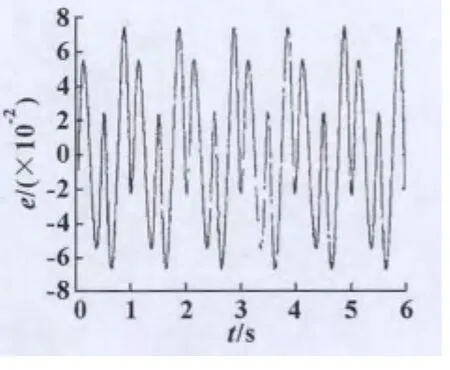
图9 车桥的正弦跟踪误差曲线

4 结论

从上面的试验结果可以看出，文中用到的基于BP神经网络的PID控制具有很好的自适应、自调整功能，对电液伺服位置控制系统具有很好的控制效果，解决了常规PID控制过程中参数不能自整定的问题，控制器具有自学习、自适应的优点，具有很好的应用价值。

［1］何玉彬，刘艳秋，徐立勤，等.电液伺服系统的神经网络在线自学习自适应控制［J］.中国电机工程学报，1998，18(6):434－437.

［2］张泽旭.神经网络控制与MATLAB仿真［M］.哈尔滨:哈尔滨工业大学出版社，2011:56－72.

［3］娄磊，杨逢瑜，王顺，等.模糊PID控制在电液伺服系统中的应用［J］.液压与气动，2009(7):52－54.

［4］李士勇.模糊控制，神经控制和智能控制论［M］.哈尔滨:哈尔滨工业大学出版社，1998.

［5］冀宏.液压气压传动与控制［M］.武汉:华中科技大学出版社，2009.

［6］HUNT K J，SBARBARO D，BIKOWSKI R，et al.Neural Networks for Control Systems:A Survey［J］.Automatica，1992，28(6):1083－1112.

［7］梅红伟.多通道汽车疲劳试验台的测控系统的设计［D］.成都:西南交通大学，2006.