基于模糊神经网络滑模控制的xy平台轮廓控制

王丽梅，左莹莹

(沈阳工业大学电气工程学院，辽宁沈阳110870)

数控加工系统的发展方向是高精密、高速度和高复合化。直接驱动xy平台已经被广泛用于高速自动化加工领域［1］。其轮廓精度是单轴跟踪精度和双轴联动精度的合成。为提高轮廓精度，很多方法侧重于设计单轴控制器，间接地减小整个系统的轮廓误差。例如，文献［2］采用零相位控制抑制了机械延迟对加工系统的影响。文献［3］采用积分滑模设计了位置控制器，文献［4］也采用滑模变结构控制进行了位置环和速度环控制器的设计。其共同的缺点是存在抖振问题且控制比较复杂。文献 ［5］阐述了智能控制在直线电机上的应用。随着智能控制的出现，将现代控制方法与智能控制方法相结合已成为学者们研究的方向。例如，文献［6］将模糊控制和滑模变结构控制相结合设计了模糊自学习滑模控制器来抑制系统参数变化和外界扰动对系统的影响，其缺点是模糊控制处理信息能力差。文献 ［7－8］采用神经网络控制和滑模控制相结合对直线电机进行了控制，其缺点是神经网络控制连接权之间物理意义不清晰且不能完全消除抖振问题，其优点是并行处理信息能力较强。文中将三者结合取其互补性，使模糊神经网络滑模控制不但连接权之间物理意义清晰，而且具有较强的并行处理信息能力，提高系统鲁棒性的同时基本能够消除滑模变结构控制自身存在的抖振问题。针对直接驱动xy平台采用此控制方法进行单轴控制器的设计，使单轴具有较好的跟踪精度，间接地减小轮廓误差。但是单纯提高单轴跟踪精度不能完全解决轮廓误差模型复杂对轮廓精度的影响，因此为了直接地减小整个系统的轮廓误差，进一步提高直接驱动xy平台对自由轨迹的跟踪能力，也有学者做了研究［9］。其控制思想是首先建立曲线轨迹的轮廓误差模型;然后以轮廓误差作为直接被控量，通过控制器的调节来直接地改善系统轮廓精度。

文中首先采用FNNSMC设计单轴位置协调控制器，用以削弱负载扰动对单轴跟踪精度的干扰;其次采用实时轮廓误差估计法对任意轨迹的轮廓误差进行建模并采用CCC来分配xy两轴的补偿值，使误差量在有限时间内趋近于零，削弱轮廓误差模型复杂对系统性能的影响，以满足PMLSM直接驱动xy平台的高精度加工要求。

1 直接驱动xy平台轮廓误差模型

精确的轮廓误差模型有利于提高直接驱动xy平台数控系统的轮廓加工精度，图1为任意轨迹的实时轮廓误差模型。其中期望轨迹的加工位置R1(t)，实际轨迹的加工位置是P1(t)且期望轨迹上的一点是R'2(t)，假设从R'2(t)到R1(t)所需的加工时间为Δt，ex是x轴跟踪误差，ey是y轴跟踪误差，x轴与直线R1R'2的夹角是φ。

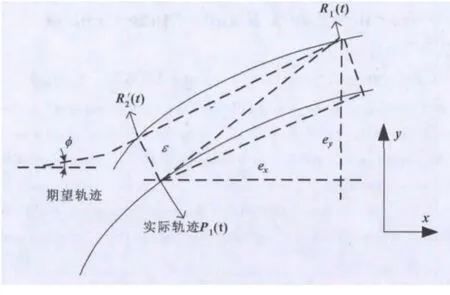
图1 任意轨迹的实时轮廓误差

轮廓误差为P1(t)到直线R1R'2的距离ε，vR1为点R1(t)的平均速度，vP1为点P1(t)的平均速度，v1和v2分别为R1(t)、R'2(t)两点的切线速度，且下角标x，y分别代表x轴和y轴。由以上这些推出

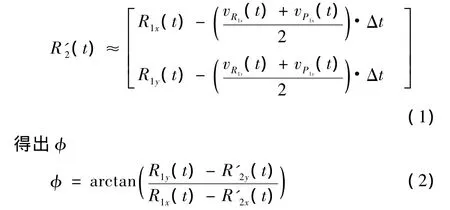
最终推导出任意轨迹轮廓误差公式为

2 模糊神经网络滑模控制器设计

直接驱动xy平台是由轴向垂直运动的两台PMLSM驱动的，由PLMSM工作原理可得其单轴状态空间方程为

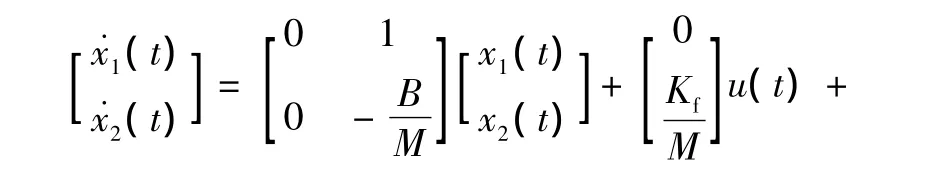
式中:［x1(t)x2(t)］T=［xrvr］，Tf为外部扰动且定义跟踪误差公式为

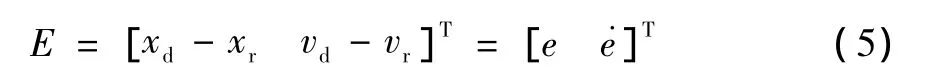
假如速度信号 定义为如下形式

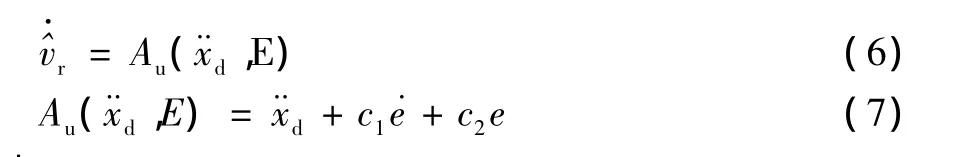
式中:c1＞0，c2＞0。

定义滑模面切换函数为

当S(t)=0时满足vr=^vr，并且将式 (8)代入式 (6)和 (7)中，可以得到式 (9)

上式满足t→∞时e(t)→0，则滑模的等效控制为

式中:UFNN为FNNSMC的输出，用来代替常规滑模的等效输出。

文中采用含输入层、隶属度函数层、规则层和输出层的4层模糊神经网络结构如图2所示。

图2 4层模糊神经网络滑模控制结构图

定义一个李雅普诺夫函数为v=0.5S2则

式中:满足当t→∞时S(t)→0，为了使S S·极小化，定义S(t)和S·(t)为所设计控制器的输入。

第1层:输入层

第2层:隶属度函数层

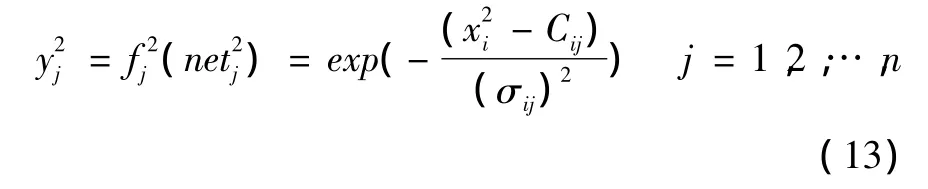
式中:Cij和σij分别为高斯型隶属函数的均值和标准差。

第3层:规则层

第4层:输出层

定义目标函数为

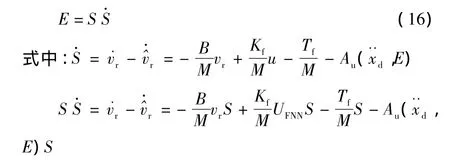
通过如下方式来调整输出层的权值

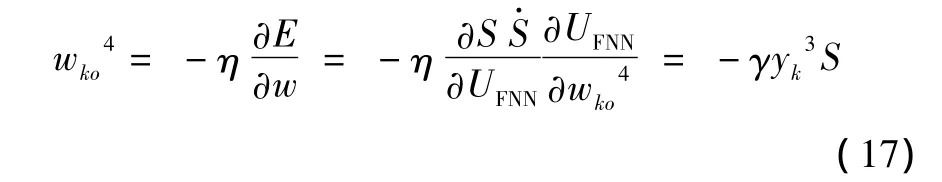
定义规则层和隶属度函数层的误差项为通过如下方式来调整隶属度函数参数

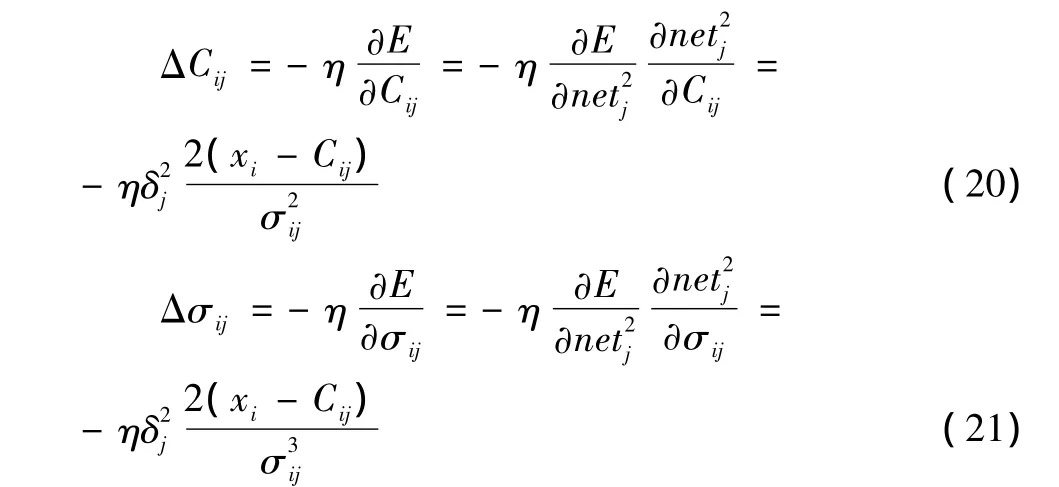
直接驱动xy平台系统轮廓控制结构如图3所示，其中xd，yd和xa，ya表示单轴的输入输出，ξx和ξy分别为x、y轴的负载扰动，轴间交叉耦合控制器采用实时性较强的PID控制。

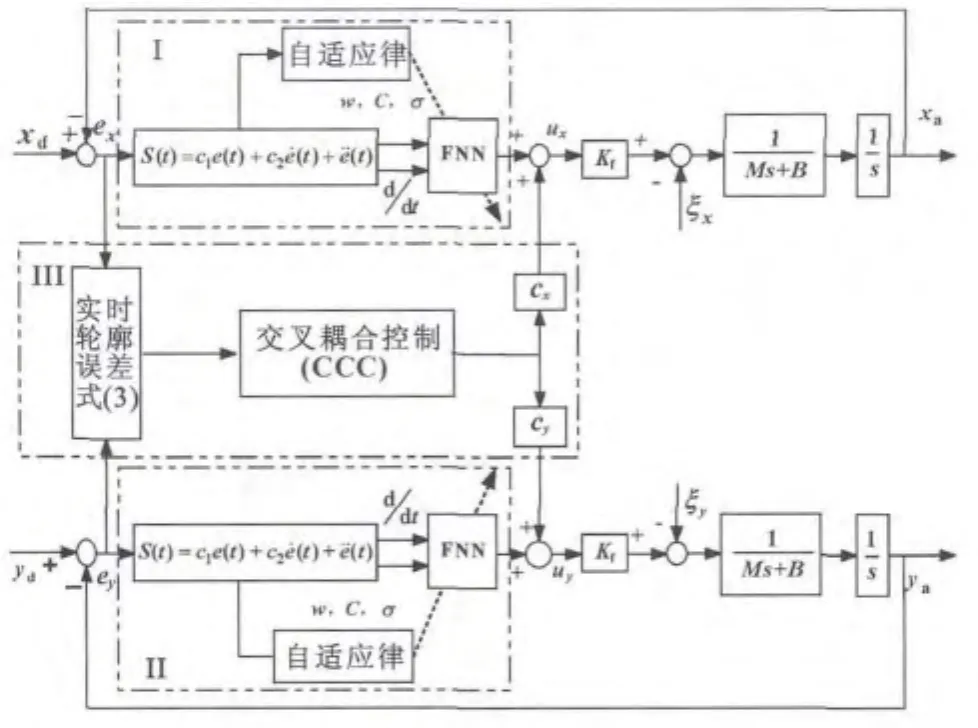
图3 基于模糊神经网络滑模控制的xy平台轮廓控制框图

3 仿真与分析

文中以心形轨迹为例，采用参数相同的两台PMLSM进行仿真，其参数如下:

m=5.8 kg，Kf=10.979 4 N/A，B=244.319 2 Ns/m，交叉耦合控制器的比例、积分、微分增益分别为15，35，5;神经网络权值w的初值取 ［－1，1］之间的随机值，中心矢量和高斯基宽向量的初始值C=［－3 －1.5 0 1.5 3］，σ= ［1 1 1 1 1］T。

图4 指令轨迹与输出轨迹

图4为xy平台的合成输出曲线。可以明显地看出:基于模糊神经网络滑模控制作用下，实际输出曲线达到了给定的心形轨迹效果。

图5(a)和 (b)分别为直接驱动xy平台单轴采用RBF神经滑模控制和模糊神经网络滑模控制下的输入响应曲线，可以明显地看出:在前者控制下，系统存在较大的抖振问题;但是在后者控制下，系统的输入信号基本不存在抖振问题，因此单轴采用模糊神经网络滑模控制有效地消除了抖振问题。

图5 x轴控制输入

图6、图7分别为t=2 s时向各轴突加500 N负载扰动的情况下，单轴采用RBF神经网络滑模控制和模糊神经网络滑模控制下的单轴位置误差曲线。可以明显看出:位置跟踪精度均达到了10－4m，但是后者的位置精度明显高于前者，而且在外界扰动存在的情况下，系统很快地跟踪上了给定信号，保证了直接驱动xy平台控制系统具有较好的抗扰性和较强的鲁棒性。

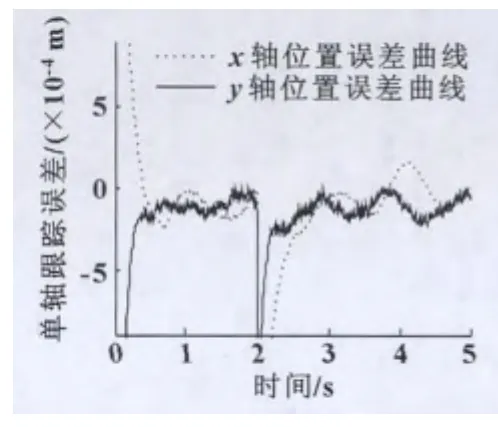
图6 RBF神经网络滑模控制+CCC时的位置误差曲线

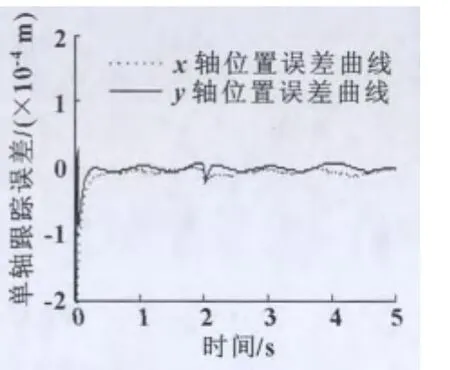
图7 模糊神经网络滑模控制+CCC时的位置误差曲线

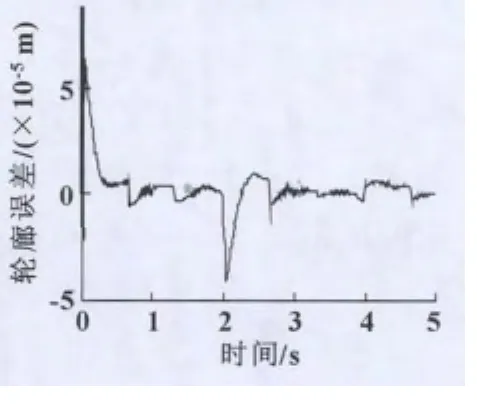
图8 轮廓误差曲线

图8为同样仿真条件下的直接驱动xy平台控制系统的轮廓误差曲线，轮廓精度达到了10－5m，与单轴跟踪精度相比有了进一步的提高，也就是说交叉耦合控制器的设计有效地减弱了轮廓误差对系统轮廓精度的影响。

4 结论

针对直接驱动xy平台加工系统，首先设计了模糊神经网络滑模位置控制器，削弱抖振的同时抑制了负载扰动对加工系统的影响;其次建立了任意轨迹的轮廓误差模型且采用传统的交叉耦合控制设计了轴间协调控制器，有效地削弱了轮廓误差模型复杂对轮廓精度的影响。仿真结果表明:所设计控制系统有效地提高了直接驱动xy平台系统的鲁棒性和轮廓精度。

［1］赵希梅，郭庆鼎.为提高轮廓加工精度采用 DOB和ZPETC的直线伺服鲁棒跟踪控制［J］.电工技术学报，2006，21(6):111 －114.

［2］赵希梅，郭庆鼎.基于ZPETC和CCC的直接驱动XY平台高精度控制［J］.组合机床与自动化加工技术，2011，21(6):111－114.

［3］王丽梅，林淑.双直线电机数控平台精密轮廓跟踪控制补偿方法研究［D］.沈阳:沈阳工业大学，2012:20－35.

［4］曾岳南，范励超.永磁同步直线电机滑模控制的研究［D］.广州:广东工业大学，2012:22 －47.

［5］吴雪芬.基于自适应神经网络的PMLSM速度控制研究［J］.电气传动，2008，38(6):37.

［6］孙宜标，郭庆鼎，孙艳娜.基于模糊自学习的交流直线伺服系统滑模变结构控制［J］.电工技术学报，2001，16(1):52－56.

［7］李海侠.遗传神经网络滑模控制在交流伺服控制中的应用研究［J］.机械设计与制造，2012(7):142－145.

［8］王伟，易建强，赵冬斌，等.一种新型神经网络滑模控制器的设计［J］.电机与控制学报，2005，9(6):603 －606.

［9］SUN Dong，SHAO Xiaoyin，FENG Gan.A Model-free Crosscoupled Control for Position Synchronization of Multi-axis Motions［J］.IEEE Transactions on Control Systems Technology，2007，15(2):306－314.