ATIS环境下随机动态路网行程时间可靠性0
2014-07-18郭洪洋张玺刘澜马亚峰
郭洪洋,张玺,刘澜*,马亚峰
(西南交通大学a交通运输与物流学院;b经济管理学院,成都610031)
ATIS环境下随机动态路网行程时间可靠性0
郭洪洋a,张玺b,刘澜*a,马亚峰a
(西南交通大学a交通运输与物流学院;b经济管理学院,成都610031)
为评价随机动态道路网络系统在ATIS环境下的行程时间可靠性,将出行者群体划分为装载和未装载信息接收设备两类,并假设他们均遵循随机动态用户最优原则(SDUO)进行动态路径选择,运用动态均衡理论建立了基于路径的混合SDUO不动点模型,并证明该模型至少存在一个不动点.使用离散随机变量序列描述需求的随机动态变化,基于Monte Carlo模拟和对角化相继平均算法(MSA),提出了ATIS环境下随机动态路网的行程时间可靠性评价方法.随后通过算例验证了可靠性评价方法的可行性.数值结果表明:OD行程时间可靠性随出发时段动态变化,且在动态情形下,扩大ATIS市场占有率并不能进一步提高可靠性,反而可能会导致可靠性下降.
系统工程;行程时间可靠性;不动点;ATIS;随机动态用户最优
1 引言
城市道路网络系统是城市经济系统的重要核心子系统,其性能稳定性是保障城市经济健康快速发展的必要条件.由于随机因素(如交通事故、恶劣天气等)干扰,道路网络系统常处于非平稳状态,这将导致服务水平下降,出行成本增加,随之产生交通拥堵、环境污染等社会问题.借鉴可靠性工程领域的理论方法,国内外交通学者提出了大量可靠性指标体系来评价随机路网系统的性能稳定性,以此作为交通规划和管理控制决策的参考依据.从不同角度可以定义不同的指标,如常用的连通可靠性[1]{Wakabayashi,1992#135}、行程时间可靠性[2]、容量可靠性[3],以及对这三种指标进行扩展所提出的高层次指标[4].在随机路网环境下,常常采用行程时间可靠性(TTR)作为衡量路网服务水平的指标[5].
通过向出行者提供实时的交通信息服务,先进的出行者信息系统(ATIS)能引导出行者制订更优的出行计划,以达到提高出行效率及路网服务水平的目的.目前,大量ATIS研究均是在假设路网已处于长期的均衡稳定状态这一前提下开展的,未考虑路网随机性,所得结论具有片面性.鉴于此,部分学者从供需随机性入手进行了相关研究[6-8].然而,该类研究在分析中大多采用静态均衡分配模型,并不能反映路网交通流的时变性,与实际情况存在一定距离.动态交通分配模型(DTA)能够描述路网时变需求下的交通流均衡模式,是实现ITS实时信息提供、实时诱导功能的重要理论模型之一.在DTA模型中,随机动态用户最优原则(SDUO)是动态用户最优原则(DUO)在随机路网环境下的推广,描述了出行者在面临不确定路网状态环境时根据实时理解路径效用最大化原则在决策点进行路径选择的行为.为此,本文基于SDUO原则给出考虑出行者总体由“有、无ATIS设备出行者”2部分构成的混合随机动态用户最优条件,并建立等价的不动点模型,提出了具有随机动态特性的OD需求影响下的路网的TTR评价方法,最后给出算例验证方法的可行性.
2离散随机动态需求
将路网表示为G(N,A),{n:n∈N}为节点集,{a:a∈A}为路段集,{s:s∈S⊂N}为起点集,{z:z∈Z⊂N}为讫点集;引入离散时间序列L={0,1,…,¯t}表示某天中的研究时间段,t∈L表示该研究时段中的子时段;(w:w∈W)为OD对集;Dw(t)表示t时段w间随机交通需求;设(rwn:rwn∈Rwn)为从节点n出发到OD对w终点的有效路径集.gwn(t)为t时段来自OD对w的需求到达节点n的流入率,0-1变量ηwn表示n是否是w的起始节点,若是取1,否则取0;‘T’为向量或矩阵的转置分别表示t时段属于w的路径流入率向量、实际行程时间向量、选择概率向量;表示路段a与路径rwn关联关系的0-1变量,若a在rwn上δarwn取1,否则取0,Δwn为相应的矩阵表示表示t时段属于w的路段流入率向量.那么表示t时段路网的路段流入率向量,满足表示t时段路段的实际行程时间向量.ωan表示路段与节点的关联关系,当路段a下游节点为n时,ωan取1,否则取0.
实际中,每日交通需求是随机动态变化的,表现为交通需求在时段内的随机变化和在不同时段上的动态分布.随机交通需求可假设服从正态分布[9,10].而每一天的OD需求在分布上呈现早晚2个高峰,其余时间平峰的形状.因此,同时考虑交通需求的随机性和动态性更符合实际,为此本文引入离散随机序列表示研究时间段内的随机动态需求.
令t时段w的随机交通需求Dw(t)服从均值为dw(t)方差为αdw(t)的正态分布,记为

式中α为随机需求方差的关联系数.为简化问题复杂性,设OD对在不同时段的随机需求的分布相互独立:
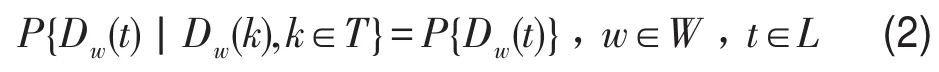
考虑整个研究时间段,任意w的离散随机需求序列可记为
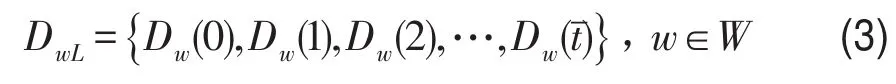
由式(2)可知,离散随机需求序列中的随机需求元素间相互独立,式(3)可视为一个随机向量,通过随机抽样技术可以方便地模拟交通需求的随机动态变化.
3 混合SDUO不动点模型
假定出行者在起点或路网中间节点上选择其所理解的最短路径出行,这时该路径选择行为符合SDUO原则[11].在该原则下,路网的均衡流量分布状态就是SDUO状态.
假设ATIS能较准确地反映当前路网状态,那么装载ATIS设备的出行者对路网实际状态的理解误差很小.而未装载ATIS设备的出行者就无法获得较准确路网状态信息,相应的理解误差很大.采取与参考文献[8]类似的处理,本文将出行者群体划分为装置和未装置ATIS设备两类,并假设他们均遵循SDUO原则进行路径选择,两类用户路径选择行为差异主要体现在不同的理解方差.设出行者理解误差服从独立同分布的Gumbel分布,且ATIS用户群的分离系数为θ1,非ATIS用户群分离系数为θ2,t时段w间两类出行者在任意决策点的路径选择概率符合Logit选择概率.这时2类出行者群体的路径选择行为符合SDUO原则.
动态环境下,实际路径行程时间是由不同时段的实际路段行程时间构成的,这与静态环境下的路径行程时间有本质区别.实际路段行程时间常常由实际流入率、流量、流出率共同确定,参考文献[12]指出路段流量、流出率实际上可以由先前时段的流入率确定,这表明影响路段行程时间的关键变量是流入率.为了简化表述,本文仅考虑流入率变量对行程时间的影响.引入关于路段流入率的示性函数ζa(t)描述路段与时段间关联性:
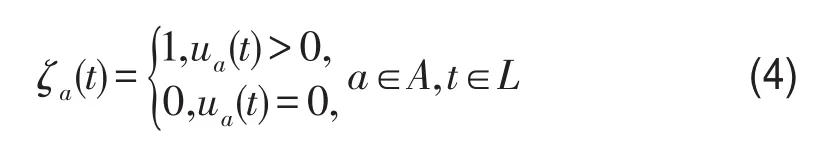
若出行者在t时段出发,并在未来某个K时段到达目的地,这时实际路径行程时间为
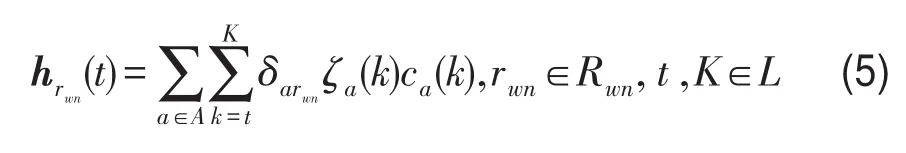
设πrwn1(·)和πrwn2(·)分别为2类出行者的Logit选择概率函数,均是路径行程时间向量hwn(t)的函数,则两类出行者的路径选择概率为
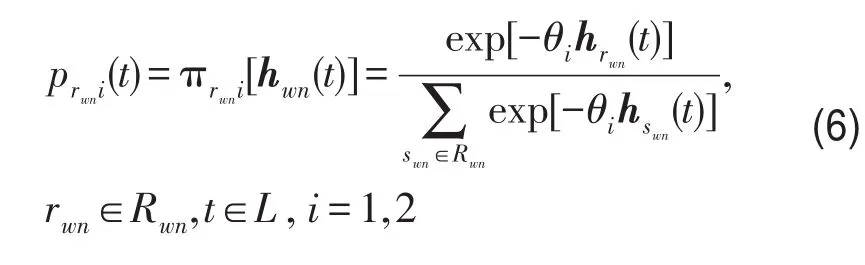
设ATIS市场占有率为φ,既ATIS用户占总需求的比例,则t时段从n沿rwn驶向w终点的路径流入率向量为
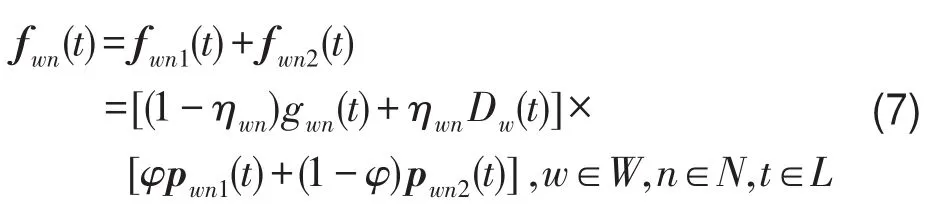
根据路段—路径的关联关系,对所有OD对路径流向量集计,则t时段路段流入率向量为
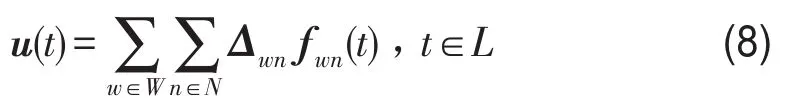
设路段阻抗函数为τa(·),将路段流入率向量带入路段行程时间函数得到路段行程时间向量路段流量传播规则可用如下指标函数表示:

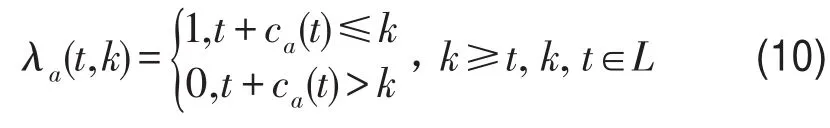
出行者在t时段驶入a后,对于未来某个k时段而言,当不等式t+ca(t)≤k成立,则该出行者至少没有在路段a上行驶,等号成立则表示出行者刚好离开路段a;当不等式t+ca(t)>k成立时,则表明出行者还在路段a上行驶.根据流量传播规则,对任意OD对w,节点n在未来k时段的节点流入率向量可以表示为
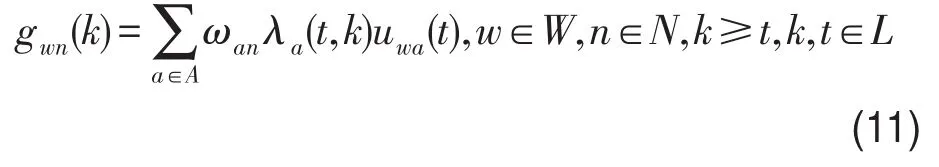
综上所述,给出混合SDUO不动点模型:
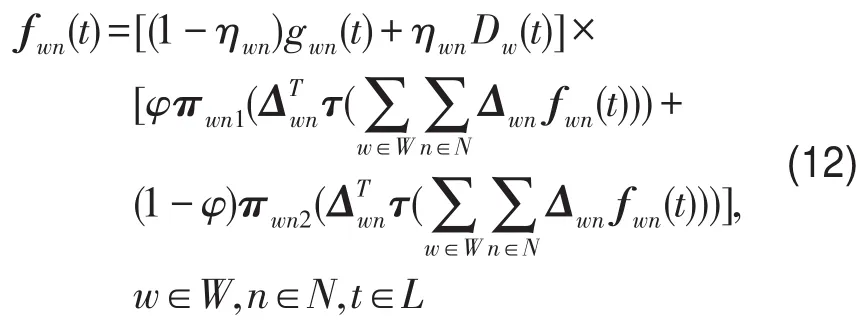
式(12)中,节点流入率gwn(t)可由过去时段的路段流入率确定,随机需求Dw(t)可用随机抽样技术确定,因此不动点问题未知量只有路径流入率向量fwn(t).
命题1式(12)给出的不动点问题至少存在一个均衡解向量.
证明:将式(12)等式右端简写为F(fwn(t)),易知fwn(t)的向量空间Ω为非空紧致凸集,且映射F:Ω→Ω的取值空间是变量空间的子集.另外Logit选择概率函数πwn1(·)和πwn2(·)均是关于路径流入率向量的连续函数,它们的凸组合仍然是连续函数,因此,由Brouwer定理可知,不动点问题至少存在一个均衡解向量,证毕.
由于时段和出行者类型具有可分离性,因此可以采用对角化算法分别对不同时段、不同出行者类型的路径流入率进行求解,然后用相继平均算法(MSA)寻找不动点问题的均衡解向量.
4 行程时间可靠性评价
本文路网系统中随机性主要源自OD随机需求和出行者的随机动态路径选择行为两方面,参考文献[13]中静态环境下TTR定义,给出动态环境下路径TTR定义:出行者从t时段出发到达目的地的路径行程时间不大于给定时间的概率,即
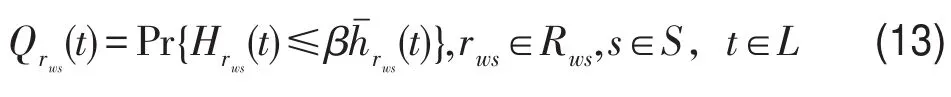
式中β为可接受水平;h¯rws(t)为给定的参考行程时间,可取OD需求均值状态下的行程时间.根据网络可靠性理论[14],可将OD对视为由多条路径构成的并联系统,以此计算OD的TTR,即
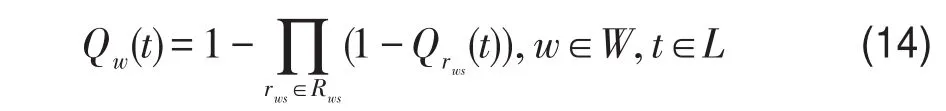
由于前文已经假设OD随机需求在每个t时段服从独立的正态分布,采用Monte Carlo随机向量抽样技术可实现OD随机需求的时变模拟及OD的TTR估计.现给出随机需求动态路网OD的TTR评价步骤:
步骤1初始化.在平均需求dw(t)下,执行对角化MSA算法求解路网SDUO状态下的路径行程时间h¯rws(t),设定β,样本数M,置样本计数器m=1.
步骤2随机抽样.根据式(3)用随机向量发生器生成各个时段的OD需求,再执行对角化MSA算法求解当前需求下的SDUO行程时间Hmrws(t).
步骤3引入指标函数:
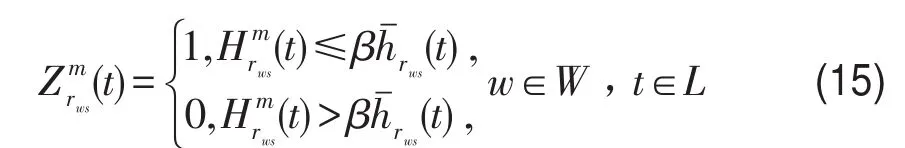
步骤4若m=M,转入下步;否则置m=m+1,返回步骤2.
步骤5停止迭代,估计各时段路径的TTR:
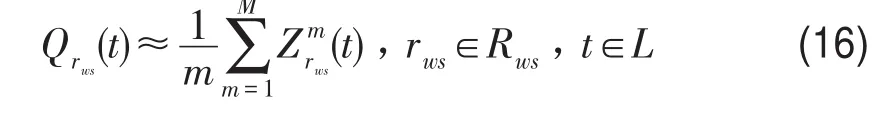
最后根据式(14)估计OD的TTR.
5 算例
算例网络如图1所示,共6节点7路段,1个OD对(1-6).路段阻抗函数采用BPR函数,不过要将原函数中的路段流量替换为t时段路段流入率:
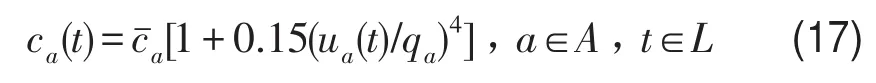
式中c¯a为路段自由流行程时间;qa为路段通行能力.各路段自由流行程时间均设定为6 min,路段1、3、5、7通行能力设为60 pcu·min-1,路段2、4、6通行能力设为80 pcu·min-1.
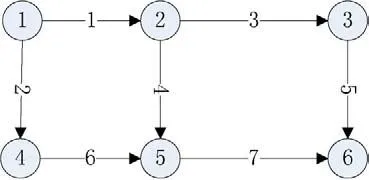
图1 算例网络Fig.1 Example network
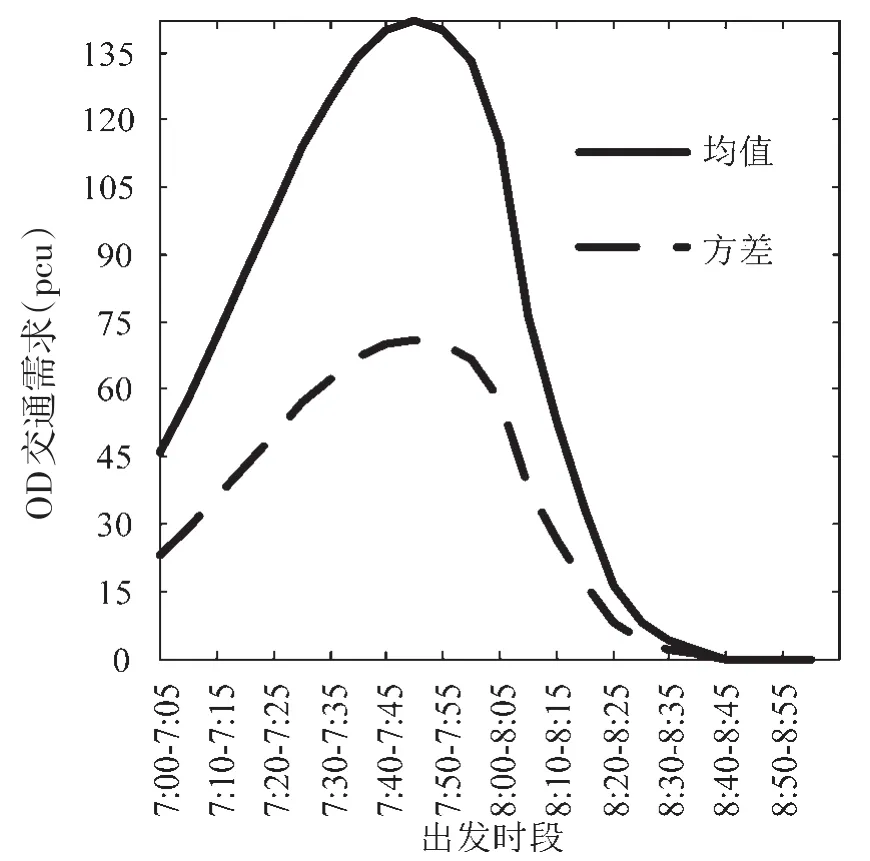
图2 随机需求均值和方差的分布Fig.2 Mean and variance distribution of stochastic demand
研究时间段为早高峰(7:00~9:00),将其划分成长度为5 min的24个时段,OD对总需求均值为1 600 pcu,随机需求方差系数α=0.5,各时段随机需求的均值和方差的分布如图2所示,7:40-7:55左右出行需求均值达到最高峰.另外,设定ATIS市场占有率φ=0.3,ATIS用户及非ATIS用户的随机误差分离系数分别为θ1=1,θ2=0.01,随机样本总数设为M=5 000.图3给出了路径1-2-3-6、路径1-2-5-6、路径1-4-5-6三路径在均值需求下SDUO状态的实际行程时间随时间的变化.可看到各路径的行程时间随需求量增加而增加,在最高峰时段7:45-7:50路径行程时间花费最长.另外,图中SDUO状态下路径1-2-5-6的行程时间比另外2条路径行程时间长,这主要是由于Logit选择概率模型独立不相关性质(IIA)所致.
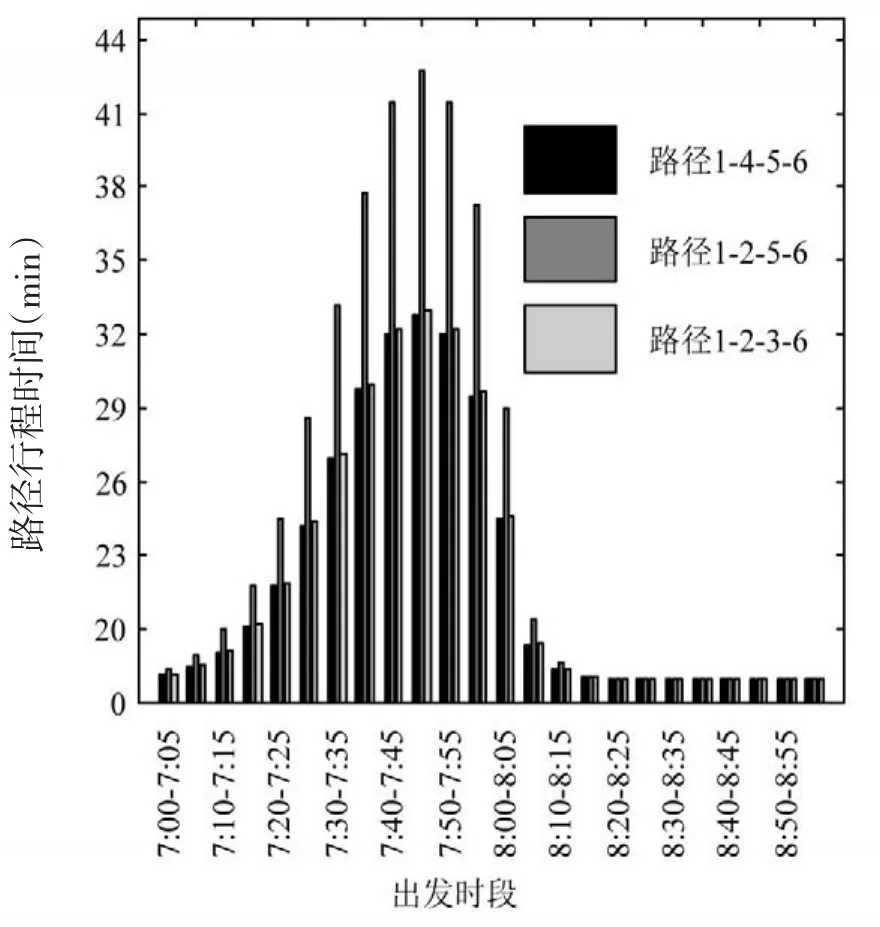
图3 平均需求下路径行程时间的动态变化Fig.3 Route travel time variation due to average demand
现考察OD的TTR随出发时段及可接受水平变化的情况,使用本文提出的可靠性评价方法计算OD的TTR,如图4所示.当在7:00-7:20时段出发,因出行需求较小,路网未出现拥挤,出行者均可在自由流状态下抵达目的地,由于理论上不可能存在小于自由流状态下的路径行程时间,因而β<1时,该时段内的TTR为0.7:20后出发的需求量逐渐增大,路网出现拥挤,出行者有可能花费比需求均值状态下还要少的行程时间抵达目的地,例如需求均值状态下7:40-7:45出发的平均OD行程时间为32.8 min,当可接受水平β=0.9时,OD的TTR为0.358 9,表明35.89%概率出行者能在29.5 min内抵达目的地.然而当可接受水平β=1时,OD的TTR为0.866 3,表明86.63%的概率出行者能在32.8 min内抵达.
现考察ATIS市场占有率对OD的TTR影响,以7:40-7:45为例,图5给出了OD的TTR在不同市场占有率下的变化,可得当占有率为φ=0.1和φ=0.3时,OD的TTR变化曲线差异不大,然而当占有率扩大到φ=0.5和φ=0.9时,可靠性下降明显.当可接受水平β=0.9时,占有率φ=0.9对应可靠性为0.267 8,而占有率φ=0.1对应可靠性为0.430 6,2者差0.162 8.这表明在动态环境下通过扩大ATIS市场占有率来改善路网性能是有限的.
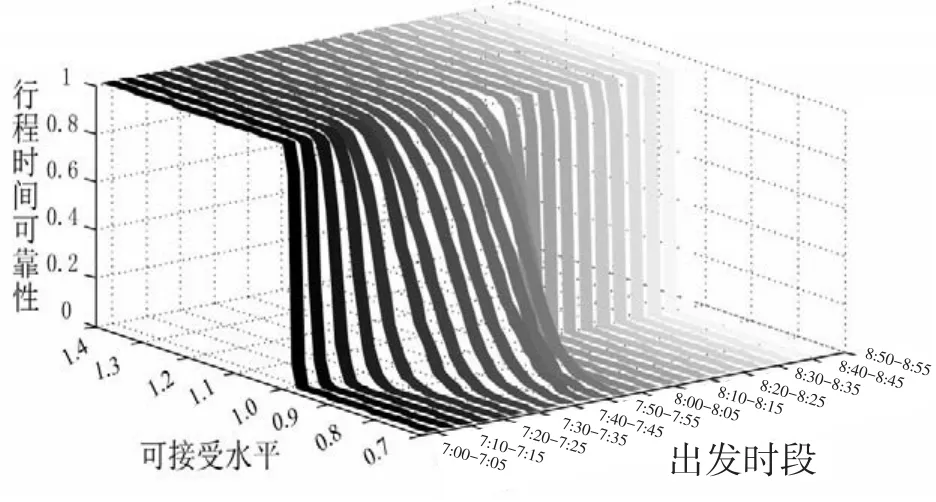
图4 OD行程时间可靠性Fig.4 OD travel time reliability
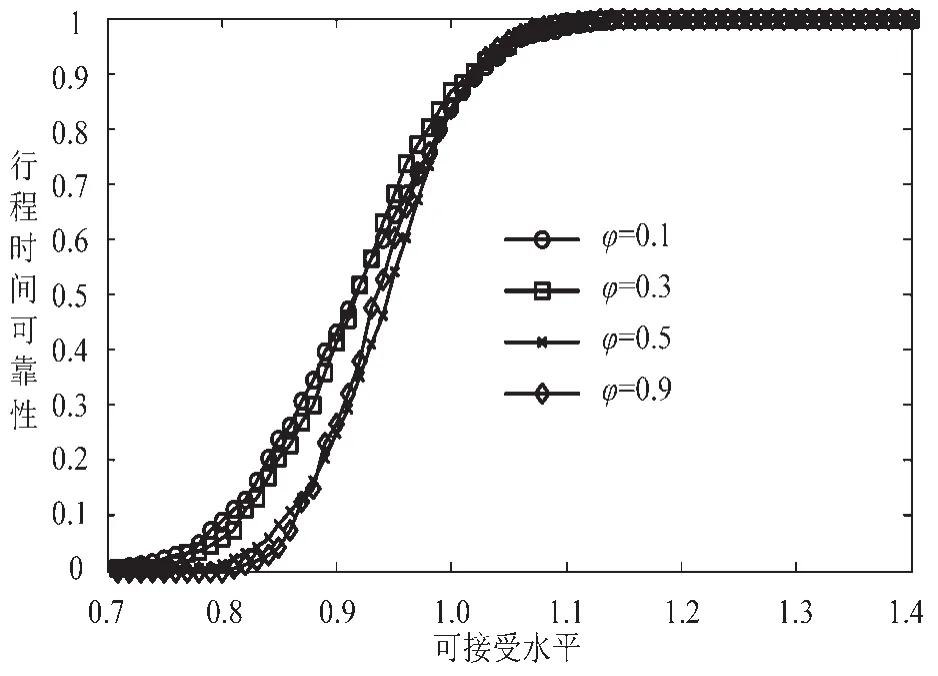
图5 时段7:40-7:45不同ATIS市场占有率下的OD行程时间可靠性Fig.5 OD travel time reliability with different ATIS market penetration rate at time interval AM7:40-7:45
6 研究结论
本文在ATIS环境下研究了随机动态路网的OD行程时间可靠性.将出行者群体划分为有无ATIS设备两类,基于混合随机动态用户最优原则建立了等价的不动点模型,并证明不动点模型至少存在一个均衡解,使用对角化MSA算法求解模型.设各时段OD需求服从独立正态分布,研究时间段内总需求在不同时段的分布表示为一个离散随机变量序列,结合Monte Carlo随机模拟技术给出了随机动态路网OD的TTR估计方法,并在算例网络上对所提出的方法进行验证.数值结果表明,该法能体现OD的TTR在不同出发时段的动态变化情况,如图4所示.此外在动态环境下,扩大ATIS市场占有率并不能提高OD的TTR,反而会导致路网服务水平下降.本文预先假设了ATIS系统能较准确地反映路网状态,忽略了信息质量的变化,而信息质量对路网状态的影响是实施ATIS时需要考虑的另一个重要方面,下一步工作中将针对不同的ATIS信息质量对随机动态路网的影响展开研究.
[1]Wakabayashi H,Iida Y.Upper and lower bounds of ter⁃minal reliability of road networks:an efficient method with Boolean algebra[J].Journal of Natural Disaster Sci⁃ence,1992,14(1):29-44.
[2]Asakura Y.Evaluation of network reliability using sto⁃chastic user equilibrium[J].Journal of Advanced Trans⁃portation,1999,33(2):147-158.
[3]Chen A,Yang H,Lo H K,et al.Capacity reliability of a road network:an assessment methodology and numeri⁃cal results[J].Transportation Research Part B:Method⁃ological,2002,36(3):225-252.
[4]王殿海,祁宏生,徐程.交通可靠性研究综述[J].交通运输系统工程与信息,2010,10(5):12-21.[WANG D H,QI H S,XU C.Reviewing traffic reliability research [J].Journal of Transportation Systems Engineering and Information Technology,2010,10(5):12-21.]
[5]Lo H K,Luo X,Siu B W Y.Degradable transport net⁃work:travel time budget of travelers with heterogeneous risk aversion[J].Transportation Research Part B:Meth⁃odological,2006,40(9):792-806.
[6]李昕,刘澜,戢晓峰.ATIS影响下的基于广义成本的随机用户平衡模型[J].交通运输系统工程与信息, 2009,9(2):50-55.[LI X,LIU L,JI X F.Stochastic user equilibrium model based on generalized cost under the influence of ATIS[J].Journal of Transportation Systems Engineering and Information Technology,2009,9(2): 50-55.]
[7]况爱武,黄中祥,张生.ATIS影响下基于广义出行负效用的随机分配[J].系统工程,2010,28(10):108-113.[KUANG A W,HUANG Z X,ZHANG S.Stochas⁃tic assignment model based on generalized travel disutil⁃ity under ATIS[J].Systems Engineering,2010,28(10): 108-113.]
[8]黄中祥,况爱武,范文婷.出行信息对道路网络出行时间可靠性的影响[J].交通运输系统工程与信息, 2012,12(6):93-99.[HUANG Z X,KUANG A W,FAN W T.Impact of traveler information on road network travel time reliability[J].Journal of Transportation Sys⁃tems Engineering and Information Technology,2012,12 (6):93-99.]
[9]Lam W H K,Xu G.A traffic flow simulator for network reliability assessment[J].Journal of Advanced Transpor⁃tation,1999,33(2):159-182.
[10]陈艳艳,梁颖.可靠度在路网运营状态评价中的应用[J].土木工程学报,2003,36(1):36-40.[CHEN Y Y, LIANG Y,DU H B.The application of reliability in the road network performance evaluation[J].China Civil En⁃gineering Journal,2003,36(1):36-40.]
[11]Ran B,Boyce D E.Modeling dynamic transportation net⁃works:an intelligent transportation systems oriented ap⁃proach[M].Berlin:Springer-Verlag,1996.
[12]高自友,任华玲.城市动态交通流分配模型与算法[M].北京:人民交通出版社,2005.[GAO Z Y,REN H L.Dynamic traffic assignment problems in urban trans⁃portation networks:models and methods[M].Beijing: China Communications Press,2005.]
[13]Asakura Y.Reliability measures of an origin and destina⁃tion pair in a deteriorated road network variable flow [C]//Proceedings of the 4th EURO Transportation Meet⁃ing,Newcastle:UniversityofNewcastleuponTyne Press,1996,25-48.
[14]Bell M G H,Iida Y.Transportation network analysis[M]. New York:John Wiley&Sons,1997.
Travel Time Reliability Evaluation of Stochastic Dynamic Road Network with ATIS
GUO Hong-yanga,ZHANG Xib,LIU Lana,Ma Ya-fenga
(a.School of Transportation and Logistics;b.School of Economics and Management,Southwest Jiaotong University, Chengdu 610031,China)
ract:To evaluate the travel time reliability of stochastic dynamic network with ATIS,this study classifies travelers into two groups:with and without the information receiving devise.Both of them are assumed to follow the stochastic dynamic user optimal(SDUO)principle to dynamically choose routes.A route-based mixed SDUO fixed point model is developed according to the dynamic equilibrium theory,which has been proved to have at least one fixed point.The stochastic dynamic demand is described as a discrete random variable sequence.Then,a travel time reliability evaluation procedure is proposed based on the Monte Carlo simulation and diagonalized method of successive average(MSA)for stochastic dynamic road network with ATIS.Then,the feasibility of the proposed approach is tested in an example network.The results show that OD travel time reliability varies as departure time interval changes,and under this dynamic case,the increasingATIS market penetration rate degrades travel time reliability instead of improving reliability.
ord:system engineering;travel time reliability;fixed point;ATIS;stochastic dynamic user optimal
1009-6744(2014)04-0073-06
U491
A
2013-11-13
2014-01-19录用日期:2014-03-27
国家自然科学基金(50908196);中央高校基本科研业务费专项资金(SWJTU09ZT18);四川省学术和技术带头人培养资金项目(川人办发[2008]24号).
郭洪洋(1982-),男,辽宁沈阳人,博士生. *
jianan_l@163.com
