振荡流通过内插螺旋翅片管传热特性的数值模拟

屈晓航，田茂诚，冷学礼

（山东大学能源与动力工程学院，山东 济南 250061）

振荡折流换热器主要利用振荡流与挡板共同作用下的强化传热传质效果，因具有把间断传热或传质过程转变为连续传热传质过程的能力，其在化工过程中得到广泛应用[1-2]。虽然平直通道中流体的振荡对强化传热作用不明显[3]，但在加入各种阻碍流体运动的障碍物的情况下，振荡流能显著强化换热[4-5]。

随着计算机技术的发展，对脉动流传热传质规律进行三维非稳态数值模拟成为可能。Jian等[6]对振荡流通过内置环形挡板通道的流动情况进行了数值模拟研究，分析了不同时刻管内流动状态图。刘成等[7]对内置环形挡板振荡流换热器内的液-液两相流进行了数值模拟，得到了振荡流参数对分散相液滴大小的影响规律。Solano等[8]数值模拟研究了内置螺旋线圈的振荡流换热器的流动传热规律，Nogueira等[9]对振荡流通过内置三孔挡板管的流动规律进行了实验和数值研究。Olayiwola等[10]用传热实验和PIV实验研究了振荡流通过内置矩形翅片通道的传热流动特性，解释了强化传热的机理，并得到了最佳翅片结构参数。

螺旋翅片作为一种新型内插物，其较大的径向高度可同时对流动起到旋转及折流作用，预期它能增大振荡流尤其是层流振荡流的掺混，并增强换热。本文使用Fluent软件对层流状态下振荡流通过内插入螺旋翅片管进行了三维非稳态数值模拟。首次以三维流线形式展示了管内瞬时流动状态。并着重讨论了振荡流参数对传热系数的影响规律，可为振荡流换热器的设计提供依据。

1 模型与方法

1.1 数学模型与边界条件

图1(a)画出了内插螺旋翅片管的结构，管内径D为20mm，螺旋片节距p、厚度e和高度h分别为30mm、0.5mm和5mm。网格划分如图1(b)所示，采用六面体网格并在靠近壁面处进行了加密。模拟采用不可压缩三维非稳态层流模型，以水为介质，物性采用水在300K下的常数，并忽略重力和黏性耗散的影响。质量、动量和能量方程的通用形式如式（1）。

不同方程对应的变量?、扩散系数Γ?和源项S?如表1所示。

管进口温度300K，使用速度入口条件，定义为式（2）。

式中，u为管进口处平均速度，随时间成正弦规律变化；un为时间平均速度，m/s；uo为速度振荡振幅，m/s；f为振荡频率，Hz。管出口使用压力出口条件，管壁及螺旋翅片壁面采用无滑移边界条件。管壁面采用恒壁温边界条件，在本研究中设为320K，翅片表面的温度应该低于管壁表面但考虑到设定边界条件的方便将翅片表面温度也设为320K。

图1 螺旋翅片结构及网格划分

表1 不同方程所对应的的?、Γ?和S?

为保证流动和传热空间充分发展，模拟选取14个螺旋翅片节距进行，管总长L为420mm。将每个时间周期划分为120个时间步长，每次模拟大于12个时间周期，以保证传热形成随时间的周期。非稳态项使用二阶隐式离散格式，速度压力的耦合采用SIMPLE算法，动量、能量方程的离散采用二阶迎风格式。

1.2 参数定义

反映振动频率特性的量纲为1的斯特劳哈尔数定义为式（3）。

主流雷诺数和振动雷诺数分别定义为式（4）。

圆管局部瞬时努赛尔数定义为式（5）。

式中，q是局部热流密度，W/m2；θ为圆管壁面周向位置，（°）；因只考虑传热充分发展区域，所以Nu数不随x变化；Twall为壁面温度320K；Tbulk为整体温度，定义为式（6）。

管周向平均努赛尔数定义为式（7）。

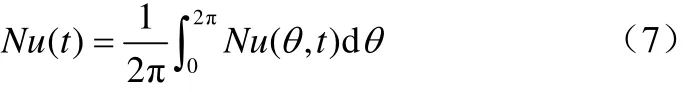
时间平均的周向平均努赛尔数定义为式（8）。

2 结果与讨论

2.1 网格无关性检查

为验证网格无关性，在管的横截面和轴向分别加密网格，网格划分方案以横截面网格数目×轴向网格数目表示。以Ren=20、Reo=40、St=4时为例，3种网格数目下（1086×756，1192×840，1334×924）周向平均Nu数在一个时间周期τ内变化规律如图2所示。最小网格数和最大网格数之间Nu误差最大为3.43%，中等网格数与最大网格数之间Nu误差不超过 1%，证明计算结果已逐渐与网格密度无关，继续加密网格已不能使计算结果更准确，综合考虑计算精度和计算时间，择优选择 1192×840划分方案，网格总数约为100万个。

2.2 验证热的空间与时间充分发展

由于进口段的影响，在流动的前若干个节距范围内，传热并不能充分发展，其Nu数沿轴向发生变化，由于水的Pr为7，速度边界层的发展远快于温度边界层，所以当传热充分发展时，可预期流动已充分发展，因此只需对传热是否充分发展进行考察。在每个节距内取一个轴向位置计算其周向平均Nu数，以一个周期内的4个时间点为例，画于图3中，横坐标为量纲为 1距离。从图 3中看出，Nu数在第5个节距以后就已经不再变化，表明传热在空间方面已经充分发展。

图2 网格无关性检查

图3 验证传热空间充分发展（Ren=20，Reo=80，St=4）

由于数值计算要给予一个各数量场的初值，初始条件也会对非稳态计算过程造成影响，即要计算充分长时间后计算结果才摆脱初始条件的影响，从图4中可以看出，在第5个时间周期后，Nu已形成周期性规律，可以认为传热已经时间充分发展。

2.3 瞬时流动与局部传热系数分析

图5画出了一个主流流速变化周期内8个时间点在主流平均速度变化曲线上的位置。图6 用三维流线的形式展示了这8个时间点的流动状态图，以便同时观察到横截面漩涡（纵向涡）和纵截面漩涡（横向涡）的产生情况。

图4 验证传热时间充分发展

图5 8个时间点在主流变化曲线上的位置

图6 一个周期内各时刻的瞬时流线图（Ren=20，Reo=80，St=4）

t/τ=0时，主流处于正向加速且加速度最大，横向看，在螺旋翅片下游靠近壁面处，流线与翅片旋转高度一致，同时在纵向有两个互相垂直的尺寸占据半个节距的涡。t/τ=0.125和t/τ=0.25分别是流体正向加速过程和速度最大的位置，它们流动状态相似，纵向看基本无横向涡形成，横向看有很弱的纵向涡形成。t/τ=0.375时，流动开始正向减速，纵向涡比前一时刻强，横向涡也开始出现，并且在翅片下游涡最明显。t/τ=0.5时，流动处于正向减速过程且减速度最大，此时纵向涡和横向涡都非常强烈，且涡尺寸与节距相当。t/τ=0.625时，流动变为反向，纵向涡仍然很强烈，横向涡比前一时刻有较大减弱。t/τ=0.75，速度达反向最大，流动状态与正向最大时相似。t/τ=0.875时，流动反向减速，与正向减速过程类似，同时存在纵向涡和横向涡，且位于翅片下游，但涡处于更靠近中心的位置，流体速度大因而漩涡强度更强。

根据以上分析可知，在一个流动周期内，纵向涡存在的时间远比横向涡存在时间长。作者认为振荡流通过螺旋翅片时，由于翅片的旋转导向作用，无论流动正向或反向，与翅片螺旋结构一致的纵向漩涡始终存在。然而流动时正时负，却使位于旋向翅片间的横向涡难以较长时间维持，只能在某些时刻出现。纵向涡在强化传热的同时因不会引入很大阻力而比横向涡更有优势[11]，所以可以推测振荡流通过螺旋翅片管在强化传热的同时不至于产生太大的阻力损失。

图7画出了对应于图5中各时间点的局部Nu数，周向角度以Y轴方向为0°，只考察了10°～350°共计340°范围内的Nu数沿周向变化规律。Nu数在翅片两侧较小，而在翅片对面较大，总体成拱形分布，并在20°和340°位置各出现一个极大值。在流动的前半个周期[如图7(a)所示]，局部Nu数最大值出现在210°附近位置，即顺X方向看翅片的右斜对面位置，且随时间最大值变小，同时曲线趋于平缓。在流动的后半个周期，Nu数最大值在前3个时间点出现在150°附近位置，即顺X方向看翅片的左斜对面位置，t/τ=0.875时出现在 210°附近位置。表明局部传热系数最大值在在翅片左右两个斜对面交替到达最大值。

图7 不同时刻的局部Nu数（Ren=20，Reo=80，St=4）

2.4 周向平均传热系数随振荡流动参数的变化

图8、图9分别是在不同振荡参数下，周向平均努赛尔数Nut随时间变化规律，图中画出了两个时间周期。可以看出，Nut随时间成周期性变化，但其变化曲线形状明显偏离外加的正弦速度变化曲线，在一个周期内出现两个波峰两个波谷，前半周期只有一个波谷，后半周期有一个波谷两个波峰，Nut在后半周期内的波动远比前半周期剧烈。

图8用相同线型的直线画出Nut对应的Nu的值。可以看出，周向平均努赛尔数Nut随St增大其波动程度越来越大，同时后半周期内的两个波峰逐渐靠近，一个波谷逐渐消失。时间平均的周向平均努赛尔数Nu却变化很小，表明St的增大即振荡频率的增大，只能使Nut波动程度变大而不能提高平均换热系数。从图9可以看出随Reo的增大，即振荡速度振幅的增大，Nut明显增大，但是其波动程度没有明显变化。同时时间平均的周向平均努赛尔数Nu也明显随Reo的增大而增大。在模拟涉及的振荡参数范围内，相比层流恒壁温条件下Nu理论值3.66，Nu最大可增强4倍。

图8 传热系数受斯特劳哈数影响规律（Ren=20，Reo=40）

图9 传热系数受振动雷诺数影响规律（Ren=20，St=4）

3 结 论

使用Fluent对内插螺旋翅片的振荡流换热器进行了数值模拟，得到了不同时刻的流动状态图和局部传热系数，并分析了振荡参数对传热系数的影响，得出以下主要结论。

（1）一个振动周期管内不断产生纵向涡和横向涡，纵向涡一直存在，而横向涡间断出现，有利于在提高换热能力的同时尽可能减少阻力损失。

（2）局部传热系数受管内流动状态影响，其分布随时间变化，总体来看，在翅片两侧较小，在翅片对面较大，且最大传热系数在翅片正对面两侧交替出现。

（3）振荡流和螺旋翅片的共同作用，使传热得到强化，传热系数随时间周期变化，瞬时传热系数和平均传热系数都随振动振幅的增大而显著增大，但振动频率的增大引起瞬时传热系数波动度增大的同时却对平均传热系数影响较小。

[1]Gao P，Ching W H，Herrmann M，et al.Photooxidation of a model pollutant in an oscillatory flow reactor with baffles[J].Chemical Engineering Science，2003，58（3-6）：1013-1020.

[2]Reis N，Mena P C，Vicente A A，et al.The intensification of gas–liquid flows with a periodic，constricted oscillatory-meso tube[J].Chemical Engineering Science，2007，62（24）：7454-7462.

[3]Chattopadhyay H，Durst F，Ray S.Analysis of heat transfer in simultaneously developing pulsating laminar flow in a pipe with constant wall temperature[J].International Communications in Heat and Mass Transfer，2006，33（4）：475-481.

[4]Suksangpanomrung A，Chungpaibulpatana S，Promvonge P.Numerical investigation of heat transfer in pulsating flows through a bluff plate[J].International Communications in Heat and Mass Transfer，2007，34（7）：829-837.

[5]何雅玲，杨卫卫，赵春凤，等.脉动流动强化换热的数值研究[J].工程热物理学报，2005，26（3）：495-497.

[6]Jian H，Ni X.A numerical study on the scale-up behaviour in oscillatory baffled columns[J].Chemical Engineering Research and Design，2005，83（A10）：1163-1170

[7]刘成，付存亭，张敏华，等.振荡流反应器内液-液两相流的数值模拟[J].计算机与应用化学，2012，29（8）：959-964.

[8]Solano J P，Herrero R，Espín S，et al.Numerical study of the flow pattern and heat transfer enhancement in oscillatory baffled reactors with helical coil inserts[J].Chemical Engineering Research and Design，2012，90（6）：732-742.

[9]Nogueira X，Taylor B J，Gomez H，et al.Experimental and computational modeling of oscillatory flow within a baffled tube containing periodic-tri-orifice baffle geometries[J].Computers &Chemical Engineering，2013，49：1-17.

[10]Olayiwola B，Walzel P.Cross-flow transport and heat transfer enhancement in laminar pulsed flow[J].Chemical Engineering and Processing：Process Intensification，2008，47（5）：929-937.

[11]武俊梅，陶文铨.纵向涡强化通道内换热的数值研究及机理分析[J].西安交通大学学报，2006，40（9）：996-1000.