变系数时间－空间分数阶对流－扩散方程的数值算法比较

马亮亮， 刘冬兵

（攀枝花学院 数学与计算机学院，四川 攀枝花 617000）

变系数时间－空间分数阶对流－扩散方程的数值算法比较

马亮亮， 刘冬兵

（攀枝花学院 数学与计算机学院，四川 攀枝花 617000）

文章分别采用显式差分格式、隐式差分格式和Crank－Nicholson格式，数值求解变系数时间－空间分数阶对流－扩散方程，并从局部截断误差、稳定性和计算量3个方面对数值算法进行了比较分析，通过数值算例验证了分析结果。

对流－扩散方程；有限差分格式；稳定性；收敛性；变系数

0 引 言

分数阶微分方程具有深刻的物理背景和丰富的理论内涵，近年来特别引人注目。目前，分数阶导数和分数阶积分在物理、生物、化学等多个学科领域有着广泛的应用，如具有混沌力行为的动力系统、拟混沌动力系统、复杂物质或者多孔介质的动力学、具有记忆的随机游走等。

目前相对应用较多且较成熟的方法依然是有限差分法和级数法，主要是Adomian分解和变分迭代方法。理论分析工具主要有傅里叶方法、能量估计、矩阵方法（特征值）和数学归纳法等，还有一些其他的数值方法，但大都不能作为普适性的数值方法或缺乏相对较完善的理论分析。文献［1－5］研究了分数阶微分方程数值算法，借助于一定条件下 Riemann－Liouville分数阶导数与Grünwald－Letnikov分数阶导数的等价性，用移位的 Grünwald－Letnikov技巧逼近 Riemann－Liouville分数阶导数，得到时间、空间、时间和空间分数阶扩散方程的有限差分离散近似格式，进而把相应的离散格式解释成时间、空间、时间和空间上的离散随机游走模型；文献［6］给出了变系数空间分数阶对流－扩散方程的有限差分格式，并给出了误差分析；文献［7］考虑了变系数空间分数阶扩散方程，借助于移位Grünwald－Letnikov技巧和Crank－Nicolson法，得到关于空间步长一阶、时间步长二阶收敛的无条件稳定数值离散格式，并对空间变量采用外推技术，使空间步长的收敛阶达到二阶；文献［8］考虑了时间分数阶对流－扩散方程，利用Mellin变换和拉普拉斯变换得到了此方程的基本解；文献［9］将文献［8］中的结论推广到n维全空间和半空间上，得到了相应的基本解，并考虑了空间－时间分数阶对流－扩散方程的解析解。

分数阶微分方程的数值算法研究起步不久，理论分析和对算法改进方面的研究有限。分数阶算子本身的非局部性这一特殊结构，使得分数阶微分方程比整数阶需要花费更多的计算时间和更高的存储要求。

本文考虑与时间和空间都相关的变系数时间－空间分数阶对流－扩散方程，即

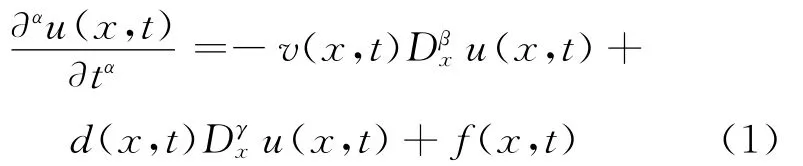
其中，0≤t≤T；0≤x≤L。

初始条件和边界条件分别为：

其中，0＜α；β≤1；1＜γ≤2；v，d≥0。

（x，t）是 Riemann－Liouville空间分数阶导数［11］，即

1 差分格式

做网格剖分，令τ、h分别是时间和空间步长，即xi＝ih，i＝0，1，…，N，h＝L／N；tk＝kτ，k＝0，1，…，M，τ＝T／M。

Riemann－Liouville空间分数阶导数采用G算法［11］，由于0＜β≤1，1＜γ≤2，所以（x，t）和（x，t）的 G 算法中，最佳移位数分别是p＝0和p＝1，即采用G1和GS（1）算法离散为：

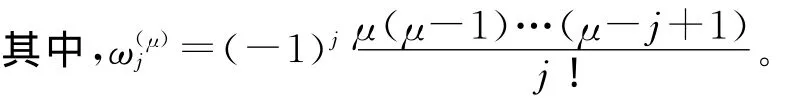
1.1 显式差分格式

令为点u（xi，tk）的近似值，即有≈u（xi，tk），则（1）～（3）式的显式差分离散可表示为：

其中，＝v（ih，kτ）；＝d（ih，kτ）；＝kτ）＝ταΓ（2－α），i＝1，2，…，N，k＝0，1，2，…，M。

初边值条件为：

其中，i＝0，1，2，…，N；k＝0，1，2，…，M。

为了简便起见，记＝rm，m＝1，2。当r1－r2γ＜2－21－α＝1－b1时，显式差分（9）式关于初值条件稳定，且（1）～（3）式的数值解与精确解的误差满足［11］：

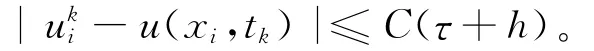
即（9）式也是条件收敛的，且收敛阶为O（τ＋h）。

1.2 隐式差分格式

使用与显式差分格式相同的时间-空间分数阶导数定义、时间与空间节点的表达方式以及步长的划分方法。

采用（1）～（3）式，可得：

或改写为：

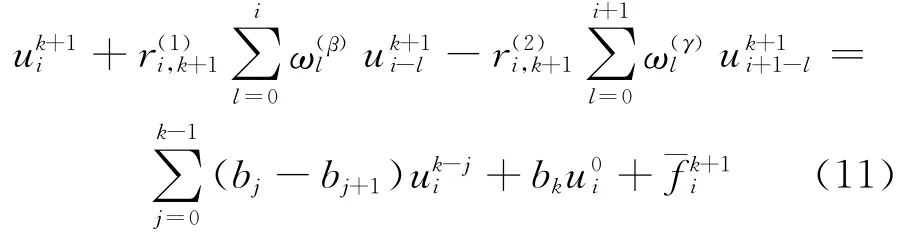
（10）式是无条件收敛的，而且收敛阶为O（τ＋h）。

1.3 Crank－Nicholson格式

Crank－Nicholson格式实质上是一种隐式差分格式，它主要是在时间方向上运用第j层与第j＋1层值的加权表示空间分数阶导数项［12］。

使用与显式差分格式相同的时间-空间分数阶导数定义、时间与空间节点的表达方式及步长划分方法，运用时间－空间分数阶导数的Crank－Nicholson格式对（1）～（3）式进行离散，可得：

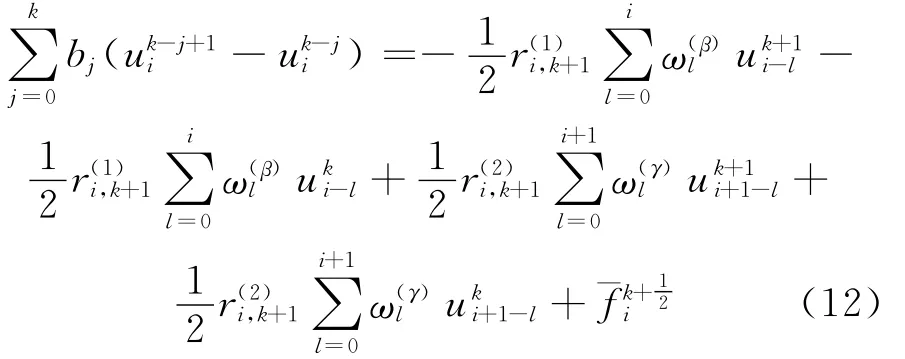
或改写为：

显然（12）式是无条件稳定的，且方程的数值解与精确解的误差满足［7］：

即Crank－Nicholson差分格式（12）式无条件收敛，且收敛阶为O（τ2＋h）。对（12）式中的空间变量采用外推技术，可进一步得到关于空间步长的二阶收敛阶离散方法。

1.4 3种差分格式的分析与比较

根据已建立的显式差分格式、隐式差分格式和Crank－Nicholson格式，分析比较3种差分格式的局部截断误差、稳定性和计算量，结果见表1所列。

从表1可以看出，对于变系数时间－空间分数阶对流－扩散方程，显式差分格式是计算量最小的一种差分格式。

但由于显式差分格式是条件稳定的，所以计算精度较差。另外，利用显式差分格式进行数值求解时，还需要注意其稳定性。隐式差分格式无条件稳定，计算量较小，且计算精度较好，是一种适中的差分方法。Crank－Nicholson格式在局部截断误差、稳定性和收敛性方面都是三者之中最好的，但其计算量也最大。

表1 3种差分格式的对比

2 数值算例

分别采用显式差分格式、隐式差分格式和Crank－Nicholson格式，对如下变系数时间－空间分数阶对流－扩散方程进行数值求解：

3种差分方法得到的数值解与精确解之间的相对误差比较，见表2所列。

表2 3种差分格式的相对误差比较（x＝0.50）

t显式 隐式Crank－Nicholson 0.1 0.001 557 755 8 0.000 135 973 6 0.000 052 805 3 0.2 0.001 305 128 2 0.000 379 487 2 0.002 307 692 3 0.3 0.001 223 241 6 0.000 103 975 5 0.000 146 789 0 0.4 0.001 103 448 3 0.000 239 310 3 0.000 137 931 0 0.5 0.000 976 640 0 0.000 308 906 7 0.000 017 066 7 0.6 0.000 862 745 1 0.000 345 098 0 0.000 249 019 6 0.7 0.000 769 574 9 0.000 216 554 8 0.000 109 172 3 0.8 0.000 671 544 7 0.000 565 853 7 0.000 455 284 6 0.9 0.000 427 256 0 0.000 172 081 0 0.000 153 856 4

从表2可以看出，显式差分格式的初始相对误差较大，而隐式差分格式和Crank－Nicholson格式则不存在该问题。另外，显式差分格式随着时间节点的增加，初始相对误差逐渐减小，但始终无法消除初始相对误差较大的问题。显式差分格式的相对误差最大，Crank－Nicholson格式的相对误差最小，与理论分析结果一致。

3 结束语

本文分析比较了数值求解变系数时间－空间分数阶对流－扩散方程的3种差分格式，通过比较发现，显式差分格式的计算量最小，但相对误差最大，且稳定性欠佳；隐式差分格式无条件稳定，但相对误差也较大；Crank－Nicholson格式的相对误差最小，且无条件稳定，但计算量最大。

除本文列举的差分方法之外，还有一些其他的近似求解方法，如有限元方法［13］、Adomian分解法［14］、配置法［15］及谱方法［16］等，但它们只能求解一些特定的对流－扩散方程，不能作为普适性的数值算法。因此，变系数时间－空间分数阶对流－扩散方程的数值计算问题还有待进一步

研究［12，17－23］。

［1］Gorenflo R，Mainardi F.Random walk models for spacefractional diffusion processes［J］.Fractional Calculus ＆Applied Analysis，1998，1（2）：167－191.

［2］Mainardi F，Gorenflo R.Approximation of Lévy－Feller diffusion by random walk ［J］.J Anal Appl，1999，18：231－246.

［3］Gorenflo R，Fabritiis G D，Mainardi F.Discrete random walk models for symmetric Lévy－Feller diffusion processes［J］.Physcica A，1999，269：79－89.

［4］Mainardi F，Gorenflo R，Luehko Yu.Wright functions as scale－invariant solutions of the diffusion－wave equation［J］.J Comput Appl Math，2000，118：175－191.

［5］Gorenflo R，Mainardi F.Discrete random walk models for space－time fractional diffusion［J］.Chemical Physics，2002，284：521－541.

［6］Meerschaert M M，Tadjeran C.Finite difference approximations for fractional advection－dispersion flow equations［J］.J Comput Appl Math，2004，172：65－77.

［7］Tadjeran C，Meerschaert M M，Scheffler H P.A secondorder accurate numerical approximation for the fractional diffusion equation ［J］.J Comput Phys， 2006，213：205－213.

［8］Liu F，Anh V，Turner I，et al.Time fractional advectiondispersion equation［J］.J Appl Math Comp，2003，13（1／2）：233－246.

［9］Huang F，Liu F.The time fractional diffusion equation and the advection－dispersion equation［J］.Anziam J，2005，46：317－330.

［10］Podlubny I.Fractional differential equations［M］.San Diego：Academic Press，1999：50－78.

［11］郭柏灵，蒲学科，黄凤辉.分数阶偏微分方程及其数值解［M］.北京：科学出版社，2011：230－247.

［12］孙洪广，陈 文，蔡 行.空间分数阶导数“反常”扩散方程数值算法的比较［J］.计算物理，2009，26（5）：719－724.

［13］Roop J C.Computational aspects of FEM approximation of fractional advection dispersion equations on bounded domain inR2［J］.J Comput Appl Math，2006，193：243－268.

［14］Momani S.Analytic and approximate solutions of the space－and time－fractional telegraph equations［J］.Appl Math Comput，2005，170：1126－1134.

［15］Rawashdeh E A.Numerical solution of fractional integrodifferential equations by collocation method ［J］.Appl Math Comput，2006，176：1－6.

［16］Liu Y，Xu C.Finite difference／spectral approximations for the time－fractional diffusion equation［J］.J Comput Phys，2007，225（2）：1533－1552.

［17］马亮亮.时间分数阶扩散方程的数值解法［J］.数学的实践与认识，2013，43（10）：248－253.

［18］马亮亮.一种Caputo分数阶反应－扩散方程初边值问题的隐式差分格式［J］.贵州师范大学学报：自然科学版，2013，31（1）：58－61.

［19］马亮亮.一种时间分数阶对流扩散方程的隐式差分近似［J］.西北民族大学学报：自然科学版，2013，34（1）：7－12.

［20］马亮亮.变系数阶空间分数阶对流－扩散方程的有限差分解 法 ［J］.沈 阳 大 学 学 报：自 然 科 学 版，2013，25（4）：341－344.

［21］马亮亮.变时间分数阶非定常对流扩散方程的数值分析［J］.辽东学院学报：自然科学版，2013，20（3）：220－223.

［22］马亮亮，田富鹏.空间分数阶Edwards－Wilkinson方程的显式差分近似［J］.沈阳大学学报：自然科学版，2013，25（3）：250－252.

［23］陈一鸣，刘丽丽，孙 璐，等.Legendre小波求解非线性分数阶积分微分方程数值解［J］.合肥工业大学学报：自然科学版，2013，36（8）：1019－1024.

Comparative study of numerical algorithms for time－space fractional convection－diffusion equation with variable coefficients

MA Liang－liang， LIU Dong－bing
（College of Mathematics and Computer，Panzhihua University，Panzhihua 617000，China）

In this paper，the explicit difference scheme，implicit difference scheme and Crank－Nicholson difference scheme are used respectively to solve the time－space fractional convection－diffusion equation with variable coefficients，and their performance is analyzed in terms of local truncation error，stability and computing expense.Finally，a numerical example is given to validate the results.

convection－diffusion equation；finite difference scheme； stability； convergence；variable coefficient

O241.82

A

1003－5060（2014）06－0757－04

10.3969／j.issn.1003－5060.2014.06.023

2013－06－28；

2013－09－28

国家自然科学基金资助项目（10671132；60673192）；四川省科技厅资助项目（2013JY0125）；攀枝花学院院级培育资助项目（2012PY08）；攀枝花学院校级科研资助项目（2013YB05）和攀枝花学院院级科研创新资助项目（Y2013－04）

马亮亮（1986－），男，甘肃天水人，攀枝花学院讲师.

（责任编辑 吕 杰）