一种基于无线传感器阵列的到达方向检测方法*

聂卫科， 房鼎益， 陈晓江， 冯大政

(1.西北大学 信息科学与技术学院，陕西 西安 710127；2.西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

计算与测试

一种基于无线传感器阵列的到达方向检测方法*

聂卫科1， 房鼎益1， 陈晓江1， 冯大政2

(1.西北大学 信息科学与技术学院，陕西 西安 710127；2.西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

以线性等距无线传感器阵列为例，提出一种有效的到达方向检测算法。列堆栈两个平移不变子阵的相关矩阵，给出一种奇异值分解和特征值分解相结合的两步算法，估计传感器阵列的导向矢量矩阵，通过分析导向矢量矩阵的结构化信息，构造估计导向矢量和理想导向矢量的相关函数，进而求解相关函数的驻点，搜索有限个驻点中使相关函数最大的驻点对应的角度估计到达方向，避免了穷尽搜索。仿真结果表明：所提算法在相同信噪比下分辨成功率高于著名的ESPRIT算法、同一分辨成功率下要求的信噪比更低。在信噪比、快拍数、阵元个数变化下对目标定位的均方根误差均优于ESPRIT算法，更接近于理论最优值。

目标定位； 到达方向； 无线传感器阵列

0 引 言

高分辨子空间类波达方向估计[1,2]利用传感器阵列估计空间目标的位置信息，是雷达、声纳、移动通信等众多领域的关键技术。在高分辨子空间算法中，MUSIC算法[3～4]需要谱峰搜索，计算量庞大。著名的ESPRIT算法[5,6]寻求一种闭式解，无需谱峰搜索，极大地减少了计算量和存储量，被认为是子空间类方法中最具应用价值的方法[7]。

本文以均匀线阵为例，构造平移不变子阵的相关矩阵，列堆栈两个相关矩阵，进而给出一种特征值分解和奇异值分解相结合的双特征分解的子空间类方法，估计阵列的导向矢量矩阵。随后，提出一种相关最大方法从估计的导向矢量矩阵中反解波达方向。仿真表明:所提算法在信噪比、快拍数和阵元数变化的情况下，均方根误差性能比ESPRIT算法更接近于最优值。

1 系统模型

考虑图1所示的含M+1个阵元的均匀线阵，相邻阵元间距为d，P个远场窄带信号以θ=[θ1，θ2，…,θp]入射到阵列，入射波长为λ，阵元间距小于半波长。

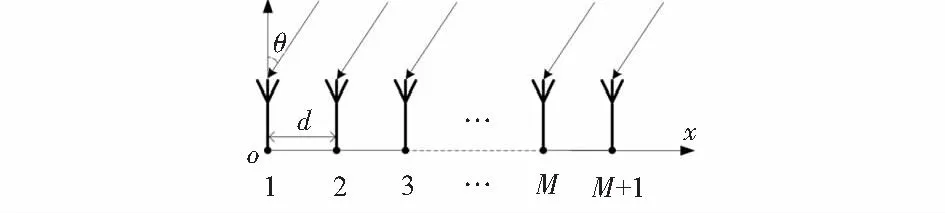
图1 系统模型Fig 1 System model

以第一个阵元为参考点，在第t次快拍下阵元m,m=1,2,…,M+1接收的P个信源的总响应为

(1)

其中,sp为第p个信源的复包络，nm为第m个阵元上的噪声。设阵元1～M为第1个子阵，阵元2～M+1为第2个子阵，则第1个子阵接收的数据向量为

x1(t)=[x1(t),x2(t),…,xM(t)]T=A1s(t)+n1(t).

(2)

第2个子阵接收的数据向量为

x2(t)=[x2(t),x3(t),…,xM+1(t)]T=A2s(t)+n1(t) =A1Φs(t)+n1(t).

(3)

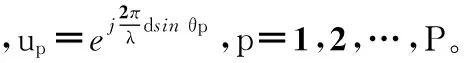
(4)

式中Rs为信源的自相关矩阵，σ2为噪声平均功率，可利用特征分解后M-P个小特征值平均估计得到，IM为M阶单位矩阵，同理,有

(5)

设C11=R11-σ2IM，C21=R21。

2 导向矢量矩阵的估计

为引出本文方法，首先给出如下定理：

定理：两个不同的矩阵X∈CM×P，Y∈CM×P，X=[x1,…,xP]，Y=[y1,…,yP]，如果M>P且rank(XHY)=P，rank表示矩阵的秩，那么,span(X)=span(Y)。

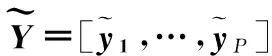
有了上述定理，将矩阵C11,C21列堆栈

(6)

设C的奇异值分解Csvd为

(7)

将式(7)写为

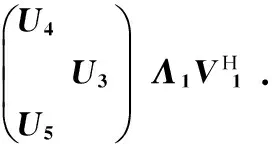
(8)

3 相关最大角度反解

有了导向矢量矩阵A1的估计，提出一种相关最大方法反解角度。设导向矢量矩阵的估计1的m行p列元素为amp，m=1,2,…，M，p=1,2,…，P。设β=jd,μ=sinθp，第p个信源的导向矢量为

a(p)=[1 eβμe2βμ… e(M-1)βμ]T.

(9)

(10)

可见当角度估计为真值时，ρ(μ)=M-1, 达到最大值，但一般估计值在真值附近摆动，因此,ρ(μ)只是一个复数，令相关函数为实数|ρ(μ)|2，则

(11)

对相关函数求导

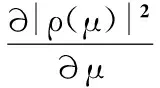
(12)

令eβμ=δ，并令式(12)为0，有

(13)

上式是关于δ的多项式，利用Matlab的求根命令Roots求出式(13)的所有零点即式(11)的所有驻点，在所有零点中找使|ρ(μ)|2最大的零点δp，从δp反解即可得角度的估计

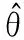
(14)

式中angle(•)表示取复数•的复角主值。

4 仿真实验

为验证所提算法的有效性，考虑M=13个间距半波长的等距线阵，接收远场P=3个窄带信号θ=(0°,5°,10°)，各阵元噪声为零均值白复高斯噪声，以下实验均为200次独立实验平均结果。

实验1：信噪比为-11～2 dB，本文算法和ESPRIT算法的分辨成功概率如表1所示。分辨成功定义为估计值与真实值的误差不超过参考角度处3 dB波束宽度的50 %，算法的分辨门限一般认为是分辨成功概率大于90 %所对应的信噪比，可见本文算法的分辨门限为-8 dB，优于ESPRIT算法0 dB的分辨门限。

表1 分辨成功概率比较Tab 1 Comparison of resolution success rate

实验2：信噪比为-5～20 dB，设n=1,2,…,N为实验次数，实验中角度估计的均方根误差RMSE定义为

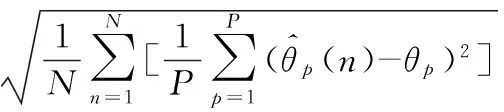
(15)

图2所示为快拍数固定在300次，不同信噪比下ESPRIT算法和本文算法及最优值的仿真曲线。由图可见，两种算法在低信噪比下性能差别较大，且两种算法离最优性能随信噪比的降低而扩大，这是由于两种算法都是建立矩阵特征分解基础上的特征结构类算法，该类算法在低信噪比下，信号空间和噪声空间的分辨误差明显增大，尤其在信号和噪声等功率的0 dB 以下，性能显著变差，随着信噪比的增加，在0～5 dB之间，两种算法性能迅速接近并趋近于最优值，在信噪比大于5 dB后，算法性能差距趋于稳定。

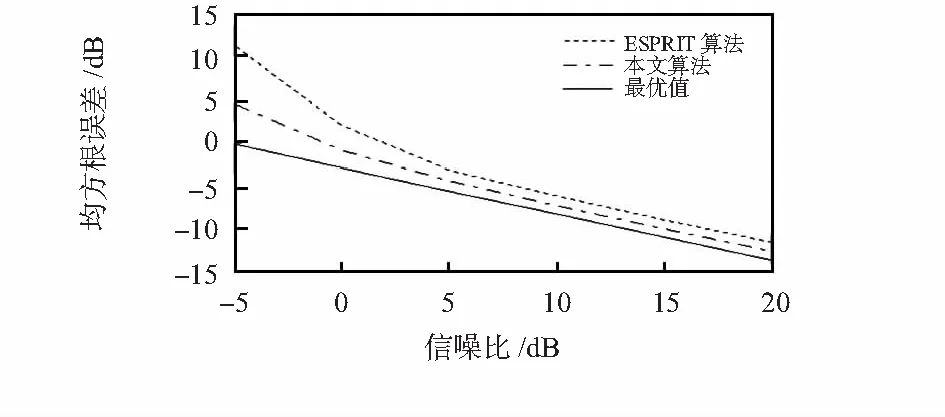
图2 角度估计的均方根误差随信噪比变化Fig 2 RMSE of angle estimation vs SNR

实验3：信噪比固定为5 dB，快拍数为100～1 000，图3所示为不同快拍下ESPRIT算法和本文算法及最优值的仿真曲线。由图可见随着快拍数的增加，两种算法对到达方向估计的均方根误差逐渐变小。

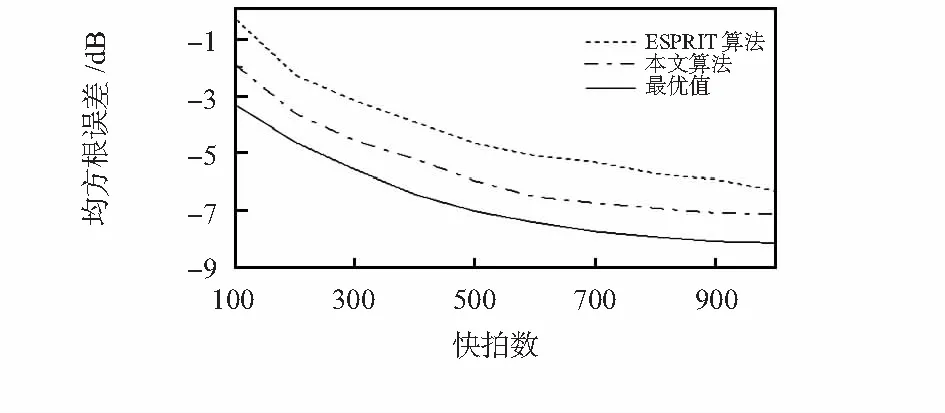
图3 角度估计的均方根误差随快拍数变化Fig 3 RMSE of angle estimation vs snapshots number

实验4：信噪比固定为5 dB，快拍数为300，图4所示为传感器阵元数变化下ESPRIT算法和本文算法及最优值的仿真曲线。

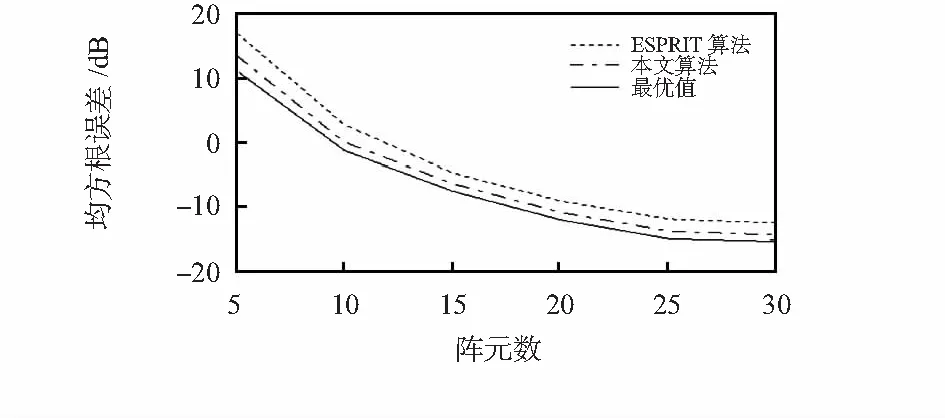
图4 角度估计的均方根误差随阵元数变化Fig 4 Change of RMSE of angle estimation vs array element number

由图可见随着阵元数的增加，两种方法角度估计更加精确，均方根误差不断减小。

5 结 论

基于相关矩阵的列堆栈，本文给出一种双特征分解的导向矢量估计方法，利用估计的导向矢量矩阵和理想导向矢量矩阵的相关函数的最大值对应的驻点求解信源的到达方向，由于相关函数的建立考虑了所有传感器的接收数据，求解的是所有特征结构的平均信息，提高了估计精度，同时,相比著名的ESPRIT算法，所提算法在相同信噪比下分辨成功率更高、同一分辨成功率下要求的信噪比更低、所提方法在信噪比、快拍数和阵元数提高的情况下，方向角估计的均方根误差不断减小，估计精度优于经典ESPRIT方法,且更接近于最优值。

但是，本文算法计算量高于ESPRIT算法，为控制计算复杂性，所提相关最大方法通过搜索有限个驻点反解信源方向，避免了穷尽搜索，计算量明显小于MUSIC类算法。

[1] Liu N,Zhang L R,Zhang J.Direction finding of MIMO radar through ESPRIT and Kalman filter[J].Electronic Letters,2009,45(17):908-910.

[2] 金 勇，程云志，周 柯.基于遗传算法的宽带目标波束空间DOA估计[J].传感器与微系统,2008,27(7):53-55.

[3] Schmidt R O.Multiple emitter location and signal parameter estimation[J].IEEE Trans on Acoustic Speech and Signal Proce-ssing,1986,34(3):276-280.

[4] Selva J.Computation of spectral and root MUSIC through real po-lynomial rooting[J].IEEE Trans on Signal Processing,2005,53(5):1923-1927.

[5] Paulraj A,Roy R,Kailath T.Estimating of signal parameters via rotational invariance techniques esprit[C]∥Proceeding of 19th Asilomar Conference on Signal System and Computes,1985:83-89.

[6] Ferreira T,Netto S,Diniz P.Direction of arrival estimation using a low complexity covariance-based approach[J].IEEE Trans on Aerospace and Electronic System,2012,48(3):1924-1934.

[7] Rouquette S,Najim M.Estimation of frequencies and damping factors by two dimensional ESPRIT type methods[J].IEEE Trans on Signal Processing,2001,49(1):237-245.

[8] Golub G H,Loan C F V.Matrix computation[M].Baltimore,MD:Johns Hopkins University Press,1989.

[9] Chabriel G,Barrere J.A direct algorithm for nonorthogonal approximate joint diagonalization[J].IEEE Trans on Signal Processing,2012,60(1):39-47.

A detection method for direction of arrival based on wireless sensor array*

NIE Wei-ke1, FANG Ding-yi1, CHEN Xiao-jiang1, FENG Da-zheng2

(1.School of Information Science and Technology,Northwest University,Xi’an 710127,Chi-na;2.National Key Laboratory of Radar Signal Processing,Xidian University,Xi’an 710071,China )

Take linear isometry wireless sensor array as example,an efficient direction of arrival detection algorithm is proposed.The correlation matrices of two shifting invariant sub-array are column stacked,then a two-step algorithm combining singular value decomposition and eigenvalue decomposition is proposed,and steering vector matrix is estimated,by analysis of the structured information of steering vector matrix,correlation function of estimated and ideal steering vector is constructed,then arrest points of correlation function are solved,direction of arrival can be given by searching the limited arrest points which correspond the maximum of the correlation function,which avoid exhaustive search.Simulation results show that the probability of resolution successful rate of proposed algorithm is higher than the ESPRIT in the same SNR,meanwhile it needs lower SNR in the same resolution successful rate.Root mean square error of target localization with the change of signal to noise ratio,snapshots number and array element better than ESPRIT algorithm,and is more closer to theoretical optimal value.

target localization; direction of arrival; wireless sensor array

10.13873/J.1000—9787(2014)12—0124—03

2014—04—21

国家自然科学基金资助项目(61373177)；陕西省自然科学基金资助项目(2013JM8008)；陕西省科技厅专项科研计划资助项目(11JK0903)

TB 556

A

1000—9787(2014)12—0124—03

聂卫科(1972-)，男，陕西渭南人，博士，讲师，主要研究领域为无线传感器网络定位与跟踪。