自适应数字滤波技术在光纤陀螺SINS中的应用*

于 飞， 阮双双

(哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001)

应用技术

自适应数字滤波技术在光纤陀螺SINS中的应用*

于 飞， 阮双双

(哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001)

光纤陀螺捷联惯导系统(SINS )对外界环境极为敏感，系统的输出信号中含有复杂的高频随机噪声，此噪声将导致系统的长时间导航精度较差。要进一步提升导航系统的精度，必须使用更为有效的滤波技术对器件的输出噪声做处理。传统的数字滤波器采用先验固定截止频率，它往往与实际截止频率存在偏差。为了更加有效地消除器件的高频噪声，提出一种基于稳态隐马尔科夫模型卡尔曼滤波器(HMM/KF)的自适应数字滤波设计方法，并用此方法设计的自适应数字滤波器处理光纤陀螺的原始输出信号，从而高效滤除陀螺仪输出信号中的高频随机噪声。

捷联惯性导航系统； 自适应数字滤波器； 自适应截止频率； 隐马氏卡尔曼滤波器

0 引 言

不论是在静态还是在系泊环境下，光纤陀螺捷联惯导系统(strap-down inertial navigation system,SINS)的惯性测量单元(inertial measurement unit,IMU)都会受到各种随机噪声的干扰，在长时间工作的SINS中，器件的高频随机噪声将一直影响系统的导航精度。为了消除随机噪声对惯导系统的影响，通常采用低阶平滑滤波器对光纤陀螺和加速度计的输出信号做处理[1,2]。随着国防工业对惯导系统高精度、低成本、高可靠性、易维护性的要求越来越严格，采用更有效的滤波技术消除惯性器件的输出高频噪声将势在必行[3,4]。传统的IIR数字滤波器和FIR数字滤波器的截止频率都采用先验固定值，通过分析惯性测量元件输出信号的频谱特性得到，与实际频率之间存在偏差[5]。

本文利用稳态隐马尔科夫模型卡尔曼滤波器(HMM/KF)和数字滤波器的等效关系，将HMM/KF的稳态参数反馈到数字滤波器中，为数字滤波器选取自适应截止频率，从而更有效地消除惯性测量元件输出信号中的高频随机噪声。

1 HMM/KF 滤波模型

隐马尔科夫模型(hidden Markov model,HMM)是一类统计模型，它包括一个不被直接观测的马尔科夫过程和一个与之相关的观测过程[6]。将HMM引入传统的卡尔曼滤波过程中，构建HMM/KF滤波方程，可以快速稳定地滤除输出信号的高频噪声。HMM作为一种强大的数学统计分析模型，已得到非常广泛的应用，在图像识别、手语识别、交通检测系统、频率跟踪、滤波、雷达目标识别,以及噪声环境下的语音识别等领域都取得了较好的效果[7,8]。

采用二维HMM对惯性器件输出建模，取HMM/KF的状态向量Xk和量测向量Zk为如下模型[6]

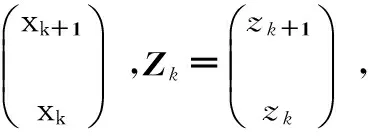
(1)

式中xk为载体真实角速度，zk为光纤陀螺陀螺输出的角速度。

HMM/KF的状态方程和量测方程为

(2)

通过对二阶HMM/KF系统的分析，可获得状态转移概率矩阵和量测概率矩阵

Fk/k-1=Hk=I.

(3)

陀螺的系统噪声方差阵和量测噪声方差阵依次为

Q=diag{q11,q22}，

R=diag{r11,r22}.

(4)

HMM/KF滤波的5个基本方程为

(5)

2 自适应截止频率的计算

HMM/KF滤波达到稳态时，系统的状态估计均方误差矩阵和滤波增益矩阵均为常值矩阵

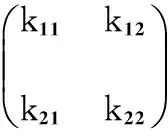
(6)

将式(6)代入式(5)Pk/k-1和Kk的表达式中得

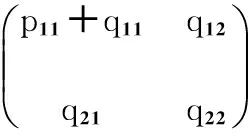
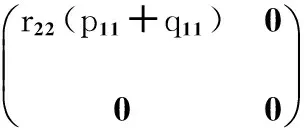
(7)

xk+1=(1-k11)xk+k11zk+1.

(8)

其中，k11=r22(p11+q11)。

将式(8)中的xk和zk+1分别用y(k)和x(k+1)代替可得

y(k+1)=(1-k11)y(k)+k11x(k+1).

(9)

对上式做z变换，系统的传递函数为

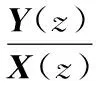
(10)

对式(10)做离散傅里叶变换，令Z=ejω

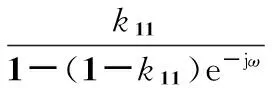
(11)

由式(11)可计算出等效数字滤波器的截止角频率为

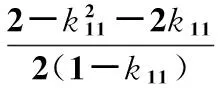
(12)

因此,该自适应截止频率为

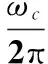
(13)

式(13)是数字滤波器的自适应截止频率的计算公式，将其引入所设计的IIR和FIR数字滤波器中，就可有效消除惯性器件输出信号中的高频随机噪声。

该方案的流程图如图1。

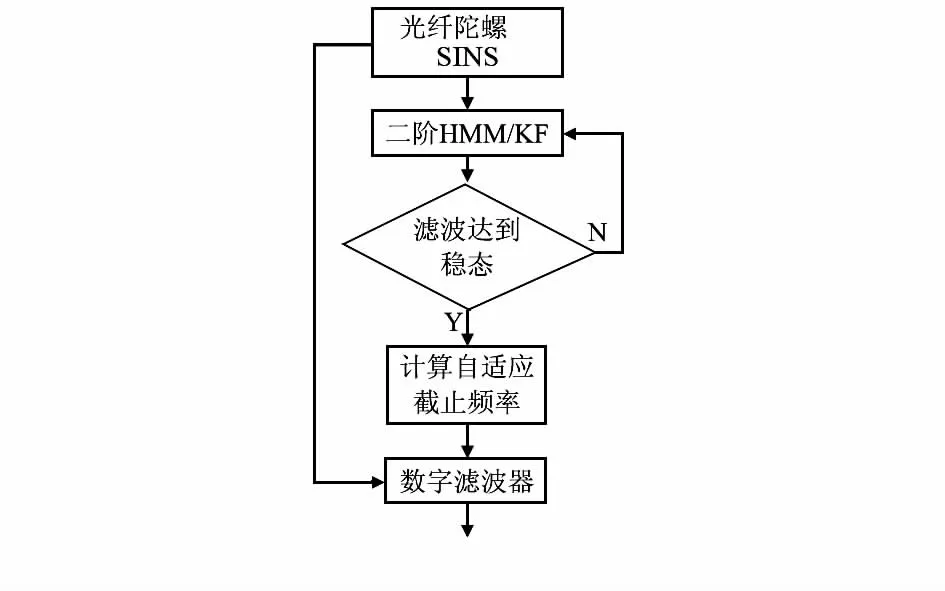
图1 基于HMM/KF的自适应数字滤波模型Fig 1 Adaptive digital filtering model based on HMM/KF

3 自适应数字滤波器的设计

数字滤波器分为有限脉冲响应数字滤波器(FIR滤波器)和无限脉冲响应滤波器(IIR滤波器)。FIR滤波器(也称非递归滤波器)仅取决于过去的输入，而与过去的输出无关，其差分方程为

(14)

因为滤波器的输出不依赖于以前的输出，所以,这种滤波器的脉冲响应为有限项。

FIR滤波器的脉冲响应为

(15)

FIR滤波器通过对理想滤波器频率特性作某种近似设计，本文选用窗函数法来近似设计FIR滤波器。根据光纤陀螺输出信号中的噪声特性，选取汉宁窗设计有自适应截止频率的FIR滤波器，汉宁窗的函数形式如下

(16)

图2是不同阶数的FIR滤波器的幅频特性曲线。

图2 不同阶FIR滤波器的幅频特性Fig 2 Amplitude-frequency characteristics of FIR filter with different orders

分析图2可得，40阶FIR滤波器的幅频特性曲线在过渡带内比较陡，阻带幅值迅速趋向0，滤波性能比较好，因此，本文取40阶FIR滤波器为基础滤波器，将自适应截止频率代入基础滤波器中得到自适应FIR滤波器。

IIR滤波器(也称递归滤波器)不仅需要过去和现在的输入，还需要过去的输出。滤波器的差分方程为

(17)

IIR滤波器通常采用模拟滤波器进行设计，考虑到巴特沃斯滤波器在通频带内的频率响应曲线最大限度平坦，且阻频带内频率响应逐渐趋于0，滤波效果较好，本文将选取巴特沃斯滤波器为模型设计有自适应截止频率的IIR滤波器。

图3给出了不同阶数的IIR滤波器的幅频特性。

图3 不同阶IIR滤波器的幅频特性Fig 3 Amplitude-frequency characteristics of IIR filter with different orders

对比图2和图3，IIR滤波器可用比FIR滤波器低很多的阶数来满足指标要求，因为IIR滤波器的输出对输入存在反馈。考虑滤波器的延迟特性和滤波器的稳定性，取4阶IIR滤波器为基础滤波器，将HMM/KF稳态参数计算的自适应截止频率反馈到基础滤波器中获得自适应IIR滤波器。

IIR滤波器由于阶数比较低，因而,所用的存储单元和运算次数少，较为经济。FIR滤波器具有严格的线性相位，且稳定性也比IIR滤波器好。在实际应用中，可以根据系统的具体要求，从多方面考虑加以选择。

4 仿真与分析

在Matlab平台上进行仿真，对实验室静态条件下光纤陀螺输出的数据进行滤波，陀螺输出数据的频率为1/98 Hz，数据长度为120 s，陀螺的原始输出信号如图4。

图4 陀螺静态原始输出Fig 4 Static original output of FOG

根据光纤陀螺的原始信号可以计算出信号的均方根值(root mean square,RMS)为10.11°/h。RMS的大小可以反映出叠加在信号中的随机高频噪声的强弱，RMS越小，光纤陀螺的输出信号越接近于真实信号，随机噪声也越弱。

首先采用四阶平滑滤波器对采样数据进行滤波，其滤波结果如图5。

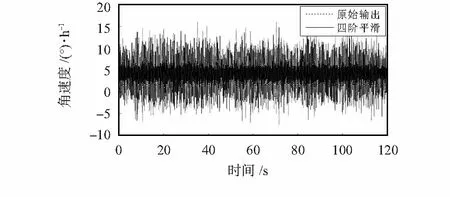
图5 平滑滤波结果Fig 5 Result of smooth filtering

图5中的毛刺是由器件随机噪声引起的，计算四阶平滑滤波器滤波后的信号的RMS为3.950 5°/h，比原始信号的RMS小，说明该滤波器能初步抑制惯性测量元件输出信号中的高频随机噪声。

下面将利用本文所设计的自适应IIR滤波器和FIR滤波器对同一组光纤陀螺的原始输出信号进行滤波。

引入自适应截止频率后的四阶巴特沃斯IIR滤波器的滤波结果如图6。

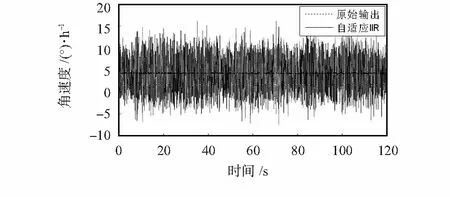
图6 四阶IIR滤波器的滤波结果Fig 6 Filtering result of fourth-order IIR filter

自适应IIR滤波器输出信号的RMS值为0.494 2°/h，与平滑滤波器相比显著减小，验证了此自适应IIR滤波器对高频噪声的抑制效果明显。

引入自适应截止频率后的40阶汉宁窗FIR滤波器的滤波结果如图7。

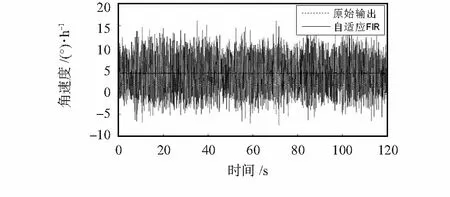
图7 40阶FIR滤波器的滤波结果Fig 7 Filtering results of 40 order FIR filter

图7中，自适应FIR滤波器输出信号的RMS值为0.369 8°/h，与图6中对应的自适应IIR滤波相比略有优势；但是图7中对应的自适应FIR滤波器到达滤波稳态的时间比较长，约为3s，而图6中对应的自适应IIR滤波器稳态时间为1.8 s。仿真结果验证了本文所设计的2个自适应滤波器可行性与实用性，它们可以有效地去除惯性器件输出信号中的高频噪声，且滤波器的截止频率可以随噪声统计特性的变化自动做出调节。

为了进一步验证自适应截止频率对系统噪声和量测噪声的自动调节能力，设HMM/KF滤波参数Q和R分别为

Q=diag{(q×0.005°/h)2,(q×0.005°/h)2},

R=diag{(r×0.01°/h)2,(r×0.01°/h)2}.

通过逐渐改变r和q的值，观察滤波增益和截止频率的变化。表1和表2说明，不同的系统噪声和量测噪声对应的数字滤波器截止频率不同，如果一味地采用先验截止频率值设计滤波器，必将影响滤波效果。因此，本文提出的自适应截止频率下的数字滤波器是很有实际应用价值的，而且简单方便。

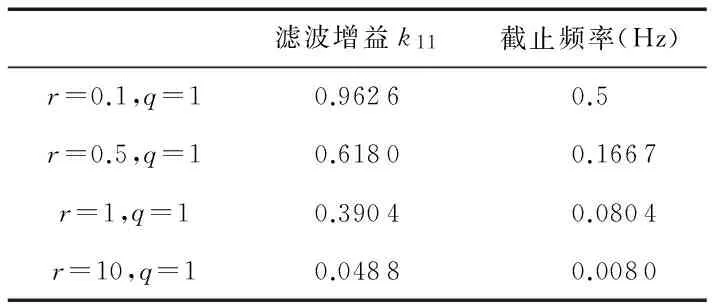
表1 不同r下的滤波增益和截止频率值Tab 1 Filtering gain and cut-off frequency with different r

表2 不同q下的滤波增益和截止频率值Tab 2 Filtering gain and cut-off frequency with different q

5 结 论

本文主要针对光纤陀螺SINS中测量元件原始输出信号的高频随机噪声，引入稳态HMM/KF的参数为数字滤波选取自适应截止频率，该频率可随系统噪声统计特性的变化而自动调节大小，从而使自适应数字滤波器更有效的消除高频噪声对系统精度的影响。仿真结果验证:本文所设计的自适应数字滤波器可显著的提高滤波精度，对惯性器件的输出高频噪声有很好的抑制效果，且滤波器设计过程简单，可用于光纤陀螺SINS的数据预处理阶段，提高系统的导航定位精度。

[1] 付强文．光纤陀螺捷联惯导系统中的误差分析与补偿[D]．西安：西北工业大学， 2005.

[2] 汪顺亭，邓 政．开环光纤陀螺仪特点及应用[J]．中国惯性技术学报，2006，14(4):93-96.

[3] 李汉舟，刘幼平，杨世超．数字滤波器在惯性测量装置中的应用[J]．中国惯性技术学报，2003，11(1):34-41.

[4] 陈江良，陆志东．基于Matlab的数字滤波器设计及其在捷联惯导系统中的应用[J]．中国惯性技术学报，2005，13(6):10-12.

[5] 郭中华，董 涌，房卫东，等．基于Matlab的FIR数字滤波器设计与仿真[J]．宁夏工程技术，2004,3(1):77-81.

[6] 曹 通．基于HMM/KF滤波的捷联惯组快速标定方法研究[J]．控制与决策，2012,27(4):1-4.

[7] Elliott Robert J,Aggoun Lakhdar,Moore John B .Hidden Markov models:Estimation and control[M].Berlin,Germany：Mathema-tics Subject Classifications，1991.

[8] Winters-Hilt S,Zuliang J.A hidden Markov model with binned duration algorithm[J].IEEE Transactions on Signal Processing,2010,58(2):948-952.

Application of adaptive digital filtering technology in optical fiber gyro SINS*

YU Fei, RUAN Shuang-shuang

(College of Automation, Harbin Engineering University, Harbin 150001,China)

The output signal of optical fiber gyroscope strap-down inertial navigation system(SINS) contains high frequency random noise as the system is sensitive to its environment,thus yielding poor long-term narigation precision.To further improve navigation precision,more effective filtering technology is needed to process output noise of device.Traditional digital filter utilize the fixed cut-off frequency which will have a deviation to its real value.In order to eliminate high frequency noise of devices effectively,a filter design method which based on HMM/KF is proposed,and the adaptive digital filter designed by this method are utilized to process original output signal of optical fiber gyro,so high frequency noise of gyro is significantly eliminated.

strap-down inertial navigation system(SINS); adaptive digital filter; adaptive cut-off frequency; hidden Markov model Kalman filter(HMM/KF)

2014—01—14

高等学校博士学科点专项科研基金资助项目(20102304110021)

U 666.1

A

1000—9787(2014)04—0154—04

于 飞(1974-)，男，教授,博士研究生导师,主要从事系统建模与仿真，载体姿态及运动参数测量技术。