一类最小方差无失真响应波束的形成方法

邵 朝, 赵 妮, 石超雄

(1.西安邮电大学 通信与信息工程学院, 陕西 西安 710121; 2.西北工业大学 航海学院, 陕西 西安 710072)

一类最小方差无失真响应波束的形成方法

邵 朝1, 赵 妮1, 石超雄2

(1.西安邮电大学 通信与信息工程学院, 陕西 西安 710121; 2.西北工业大学 航海学院, 陕西 西安 710072)

最优广义线性最小方差无失真响应波束形成往往要求阵列导向矢量和信号非圆度必须为已知，为了突破此限制，基于最小方差无失真响应方法的约束条件提出两种波束形成方法：其一是先将阵列导向矢量和非圆度的不确定性转化为整体扩展导向矢量的不确定性，再规划波束形成；其二是利用信号结构信息来规划波束形成。仿真实验结果表明，新方法在突破此限制方面具有可行性。

阵列信号处理；最小方差无失真响应；稳健的波束形成

在阵列信号处理中，波束形成是一种被广泛应用于在空间干扰信号和加性噪声的存在下增强空间传播的感兴趣的信号(Signal Of Interest, SOI)的技术[1]。传统的波束形成方法是基于二阶(Second order, SO)平稳统计快拍数据的，主要关注平稳快拍数据，由此产生了线性时不变(Time Invariant, TI)波束形成。Capon提出的最小方差无失真响应(Minimum Variance Distortionless Response, MVDR)波束形成是一个著名的线性最优波束形成方法[2]。然而，当遇到二阶非平稳信号时，传统的线性时不变方法(例如MVDR波束形成)将不是最优的。

在许多实际情况下，二阶非平稳信号也是非圆信号。为了利用快拍数据的非圆度，文献[3-4]提出基于广义线性(Widely Linear, WL)波束形成的方法并改进了性能。WL-MVDR波束形成方法[3]能够处理接收的未知信号被二阶非圆信号干扰，在平稳状态下的性能比传统的MVDR波束形成的稳定性有了较大改善。为了进一步利用SOI的非圆度而被提出的最优WL-MVDR波束形成方法[4]，利用了导向矢量的共轭部分，与传统的MVDR算法相比，在干扰为非圆信号时性能有了更大提高，输出的信干噪比(Signal Interference Noise Ratio, SINR)得到进一步改善。

根据最优WL-MVDR波束形成方法，SOI的阵列导向矢量(Array Steering Vector, ASV)的先验知识和其非圆度被假定为是可用或可预测的。然而，在许多实际情况下，精确确定SOI的ASV和实际非圆度是很困难的，这将会引起波束形成的不确定性。ASV的不确定性可能是由于接收信号时阵列响应或SOI的波达方向(Direction Of Arrical, DOA)估计误差等因素导致。非圆度的不确定性可能是由于SOI波形、相位偏移、频率偏移导致的不确定性。这些不确定性会严重降低WL-MVDR波束形成的性能，甚至比传统的MVDR波束形成性能更差。

为了解决WL-MVDR波束形成的不确定性，本文拟给出两种稳健的最优WL-MVDR波束形成的方法，它是基于传统二阶平稳快拍数据的波束形成方法，并基于MVDR方法的约束条件,分别对输入阵列导向矢量和非圆度存在不确定性的情况进行分析，推导出波束形成的加权向量表达式，最后通过仿真实验进行验证。

1 最优广义线性 MVDR波束形成

1.1 信号模型

假设一个N阶阵用来接收窄带信号，并且阵列输出为一个复矢量x(t)，它由SOI加上一个干扰噪声信号构成，即

x(t)=a·s(t)+v(t),

(1)

其中s(t)是SOI的复包络(零均值二阶非圆信号)，v(t)是干扰和噪声部分，a为SOI导向矢量。假设干扰信号为零均值、二阶非圆且与s(t)不相关。

自适应波束形成设计一般是基于信号的二阶统计量，非圆快拍数据x(t)的二阶统计量定义为

Rx=E[x(t)x(t)H]=πsaaH+Rv,

Cx=E[x(t)x(t)T]=πsγsaaT+Cv,

(2)

其中

Rv=E[v(t)v(t)H],

Cv=E[v(t)v(t)T],

而πs和γs分别是SOI的平均功率和非圆度系数，且

πs=E[|s(t)|2],

γs=E[s2(t)]/πs。

当γs=0时，随机变量为圆信号，当|γs|>0时，随机变量为弱非圆性。由Cauchy-Schwartz不等式，任何复随机变量的非圆度系数均满足|γs|≤1。特别当|γs|=1时称信号具有严非圆性[5],如二进制相移键控(Binary Phase Shift Key, BPSK)信号。

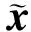
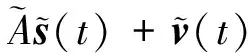
(3)

其中

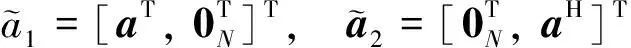
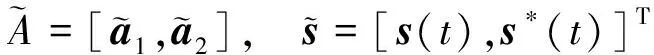
将扩展接收矩阵的扩展协方差函数定义为

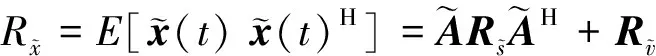
(4)

其中

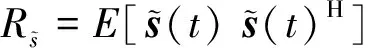
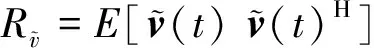
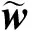
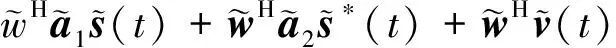
(5)

1.2 最优WL-MVDR波束形成

基于上述信号模型的建立，文献[7]通过将MVDR概念应用到扩展快拍数据中，提出了WL-MVDR波束形成。在数学上，权重矢量可以通过下面的凸规划(非线性规划)求得,即

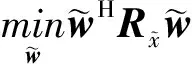
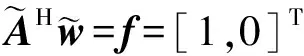
(6)

这种规划的结果可用Lagrange算子求得，结果为

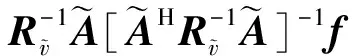
(7)

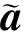
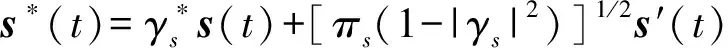
(8)

其中s′(t)是s(t)的正交信号。因此式(3)中的信号模型可以写作

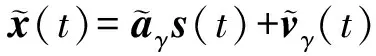
(9)

其中

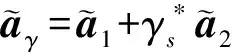
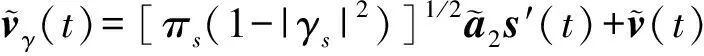
这种最优WL-MVDR可以由

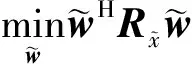
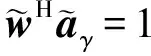
(10)

设计，通过定义

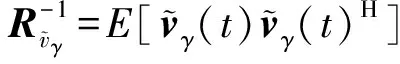
得到

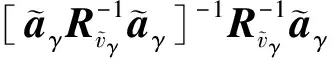
(11)

2 稳健的最优WL-MVDR波束形成

由于实际和假设参数(a，γs)之间的错配容易导致最优WL-MVDR波束形成的性能降低，而训练序列不可获得和在实际条件限制下产生的估计误差都可能导致这种错配，因此保证波束形成设计的稳定性很重要。

(12)

下面给出两种稳健方法用来处理导向矢量和非圆度的不确定性。

2.1 降低整体扩展导向矢量的不确定性

转移式(12)中约束条件的不确定性到整个增扩展向矢量的不确定性。用

分别表示感兴趣信号导向矢量和非圆度的错配产生的误差,则有

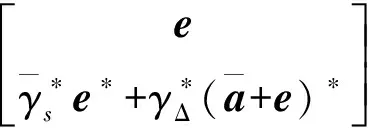
(13)

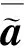
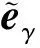
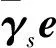
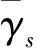
(14)

根据稳健的波束形成(Robust Capon Beamforming, RCB)公式，通过规划

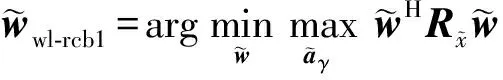
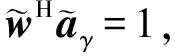
(15)

设计WL-RCB波束形成。

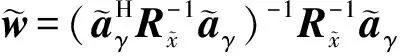
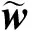
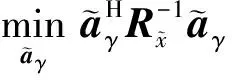
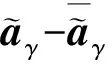
(16)

这是RCB的一种标准形式，所以可以根据标准形式的波束形成方法求得。

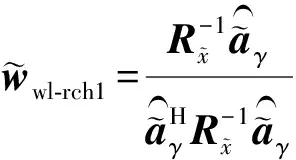
(17)

2.2 利用导向矢量结构信息提高稳健性

阵列导向矢量存在另一种结构，即

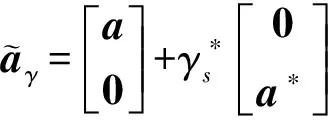
(18)

计算扩展导向矢量整体错配形式的不确定性不能利用这种结构信息，它是通过适当提高约束范围来估计的，会导致不确定性的过估计，最终会在波束形成设计时由于干扰抑制能力下降而导致SINR性能变差。

现基于稳健波束形成辅助结构的不确定性，在保持导向矢量和非圆度间结构关系的同时，分别用它们表示不确定性约束。改写式(16)，得出稳健最优WL-MVDR波束形成设计辅助结构的约束公式

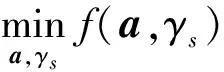
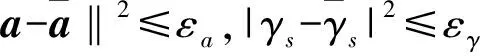
(19)

它的目标函数

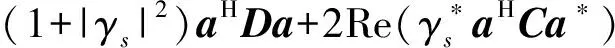
(20)

其中Re(x)表示x的实部。运用

(21)

定义求得目标函数的简化表达式,将会发现目标函数是三阶的，并不能保证凸面性，凸规划方法不能直接运用。

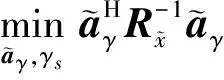
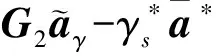
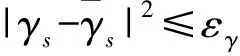
(22)

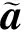
3 实验结果和分析

通过50次蒙特卡罗实验分析两种稳健WL-MVDR方法的性能。

实验中，两个窄带BPSK信号传播到阵列间距为半波长的二元阵上，入射角为0°～30°，0°为目标信号。信噪比(Signal Noise Ratio, SNR)为10～20 dB，SOI的初始相位为60°，所以

γs=-0.5 + j 0.866,

干扰信号初始相位为0。假设导向矢量错配，导向矢量的不确定性是由DOA误差引起的，设误差为3°，εγ=0.001。由于实验中不知道a和γs精确的误差，用1.2代替a和γs综合误差的平方范数ε1，这个参数值用来验证所给算法。在导向矢量错配的情况下，比较各算法的性能，结果如图1所示。可见，在不确定情况下最优WL-MVDR不再比Capon好，而两种稳健的最优WL-MVDR波束形成方法则要比Capon好。

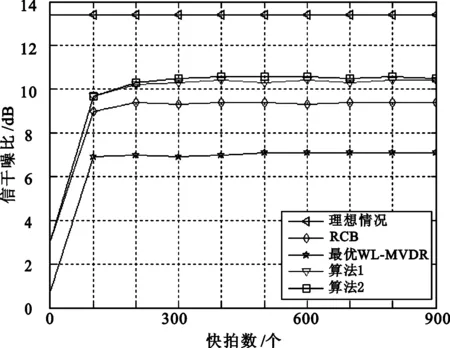
图1 信干噪比性能比较

进一步就目标信号在不同SNR输入下进行实验，以了解各算法的性能。取100组快拍数据，将波束形成的输出SINR作为比较标准，结果如图2所示，从中可见，在错配的情况下，降低整体扩展导向矢量不确定性的方法总是强于RCB和最优WL-MVDR，而利用导向矢量结构信息提高稳健性的方法在大多数的情形下比降低整体扩展导向矢量不确定性的方法好。

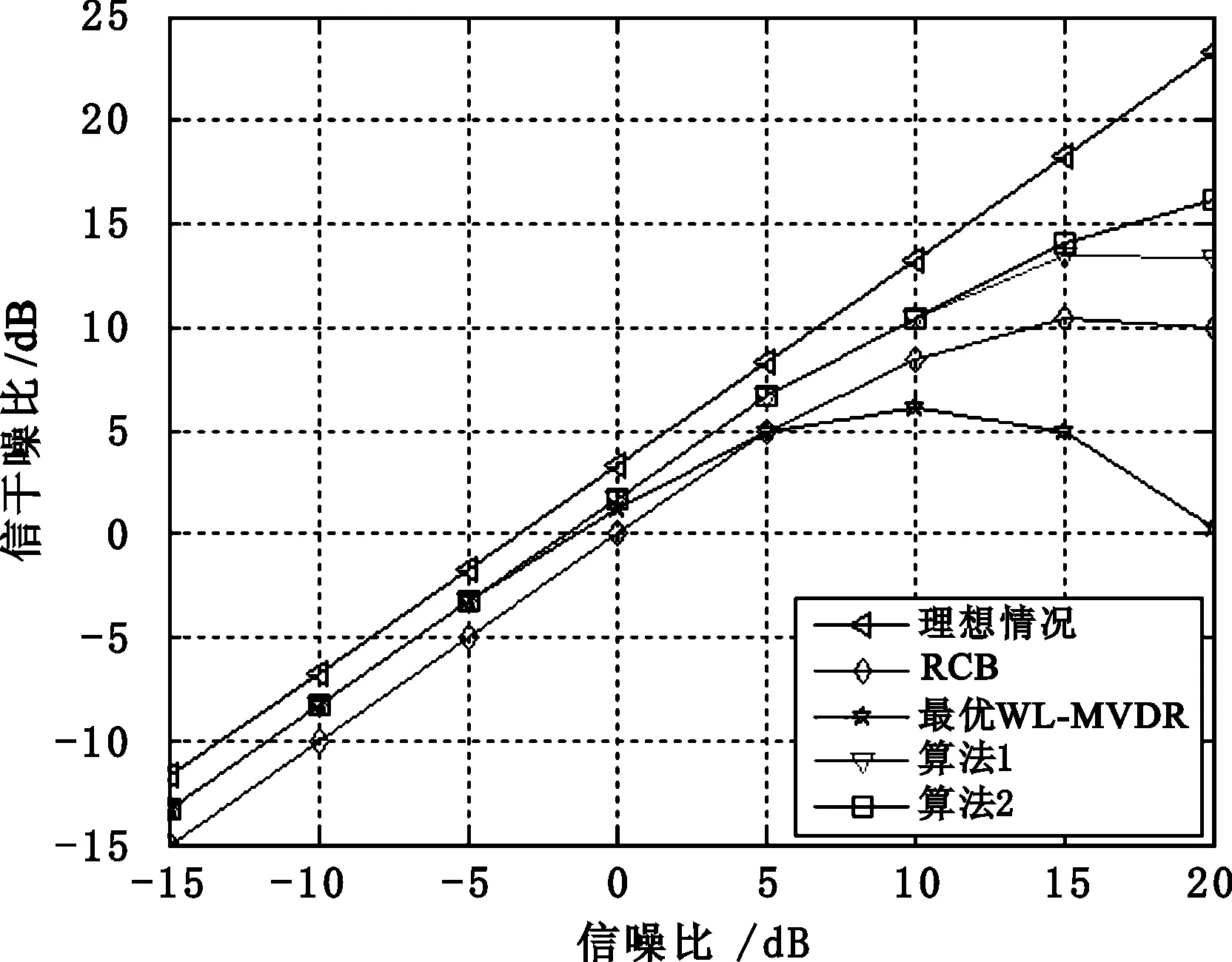
图2 输出信干噪比性能比较

4 结 语

给出了在非圆度和ASV都不确定的情况下，稳健的最优WL-MVDR波束形成算法。分别通过建立整体扩展导向矢量的不确定性和利用导向矢量的结构信息,在一定程度上解决了不确定性问题。实验表明不确定性对最优WL-MVDR和由此改进的方法性能的影响，并验证了所给新方法比传统的Capon波束形成方法有更好的性能和实用性。

[1] 董延坤,葛临东,张辉.自适应波束形成算法的现状与发展动态[J].微计算机信息,2005,21(3):64-67.

[2] 孙心宇，周建江.一种基于非圆相干信号的波束成形算法[J].宇航学报,2012,33(4):32-35.

[3] 鄢社锋,马远良.二阶锥规划方法对于时空域滤波器的优化设计与验证[J].中国科学 E辑信息科学,2006,36(2): 153-171.

[4] Chevalier P, Blin A. Widely linear MVDR beamformers for the reception of an unknown signal corrupted by nocircular interferences[J]. IEEE Trans. Sign. Process,2007, 55(11): 523-536.

[5] 刘宏清,廖桂生,张杰.稳健的Capon波束形成[J].系统工程与电子技术,2005,10(27):127-130.

[6] 何忠勇,周围.基于遗传算法的智能天线的研究[J].西安邮电学院学报,2009,14(1):29-33.

[7] Chevalier P, Delmas J P. Optimal widely linear MVDR beamforming for noncircular signals[J]. Acoustics,Speech and Signal Processing, 2009, 37(26): 3573-3576.

[8] Chevalier P, Delmas J P. Performance analysis of the optimal widely linear MVDR beamformer[J]. IEEE Signal processing, 2009, 5(17):587-591.

[责任编辑:王辉]

A class method of minimum variance distortion response beamforming

SHAO Chao1, ZHAO Ni1, SHI Chaoxiong2

(1.School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China; 2.School of Marine Science and Technolog, Northwestern Polytechnical Universety, Xi’an 710072, China)

Optimal widely linear minimum variance distortionless response beamforming normally requires available values of the array steering vector (ASV) and the signal non-circularity. To solve this strict limitation on the implementation of this beamforming, two approaches are proposed based on the limitation conditions of the minimum variance distortionless response beamforming. The first one translates the uncertainty constraints into the uncertainty for the whole extended steering vector. The second one uses the structure information of signal. Simulation results show that the two approaches can effectively implement beamforming without those limitations.

array signal processing, minimum variance distortionless response, robust beamforming

10.13682/j.issn.2095-6533.2014.03.005

2013-12-30

陕西省科技厅工业攻关计划基金资助项目(2012K06-27)

邵朝(1955-)，男，博士，教授，从事雷达阵列信号处理研究。E-mail: shaochao@xupt.edu.cn 赵妮(1989-)，女，硕士研究生，研究方向为宽带无线通信。E-mail:zhaoni123@126.com

TN911.7

A

2095-6533(2014)03-0022-04