一种改进阈值的邻域小波系数图像去噪方法

吴成茂, 胡 伟, 王 辉

(1.西安邮电大学 电子工程学院， 陕西 西安 710121; 2.西安邮电大学 自动化学院, 陕西 西安 710121)

一种改进阈值的邻域小波系数图像去噪方法

吴成茂1, 胡 伟1, 王 辉2

(1.西安邮电大学 电子工程学院， 陕西 西安 710121; 2.西安邮电大学 自动化学院, 陕西 西安 710121)

为了能更好地恢复出原图像，对基于邻域小波系数收缩的NeighShrink法进行研究。对小波域图像去噪模型加以分析，指出原方法因其阈值不能适应尺度分解所得小波系数中噪声的强弱特性，故难以保证原图像的恢复效果，随之对原方法给出一种改进，通过修正NeighShrink法中的阈值，建立起一种用指数函数调节阈值的自适应方式来匹配小波系数的幅度特性。在不同强度高斯噪声条件下的实验结果表明，改进后的方法在有效去除噪声的同时能够更好的保留原始图像信息，且相对于原方法，改进后的方法能提高峰值信噪比。

小波变换；阈值；邻域小波系数；图像去噪

数字图像在采集转换及传输过程中会不可避免地受到噪声污染，造成图像质量的退化，图像去噪是为了必要地消除尽可能多的随机加性噪声同时保留重要的图像特征。

人们研究小波系数的独立性，通过收缩小波系数，获得一种对加性白噪声非常有效的去噪方法[1-2]。这种方法将图像进行分解，并通过软硬阈值函数抑制噪声系数[3]，即令幅度低于选定阈值的系数为零，并缩小或保留幅值大于选定阈值的系数。VisuShink阈值去噪曾是一种被广泛应用的阈值技术[4-5]，后来人们又提出了BayesShink阈值选取方法[6]，此外，还有NeighCoeff 和 NeighBlock方法[7]。一般而言，基于多小波的邻域小波阈值的方法[8-9]优于基于单小波邻域系数图像去噪方法，改进阈值图像小波去噪方法(Improved Image Denoising Method based on Wavelet Thresholding, IIDMWT)[10]优于邻域小波系数法和改进邻域小波系数的算法[11]。许多基于小波变换的新技术一般都取得了较好的效果，然而如何设置一个合适的阈值依然是一个关键的问题。

本文拟利用指数函数调节子带阈值的改进因子，对小波系数采用邻域小波法的收缩因子，从而得出一种去噪方法，以改善邻域小波法和IIDMWT的性能。

1 小波域图像去噪

1.1 小波图像去噪模型

假设一幅受到噪声污染的图像模型为

Y=X+η，

其中Y是噪声图像，X为原始图像，η是均值为0且方差为σ2的高斯白噪声。由于小波变换是线性的，图像经过小波变换后，小波系数满足

WY=WX+Wη,

其中WY是小波变换后噪声图像的系数，WX是小波变换后原始图像的系数，Wη是小波变换后噪声的系数。

图像经小波变换后,能量主要集中在最低分辨率子带小波系数上,而图像的随机加性噪声经小波变换后,能量则分布在各个高分辨率子带小波系数上。

1.2 阈值选取

对于小波阈值去噪方法而言,阈值的选择非常重要,文[5]从最小最大化意义上解决了小波阈值的变分问题,提出了全局阈值

其中ση表示噪声标准差,N表示信号长度。用此阈值可对小波系数进行阈值化处理。

文[10]给出阈值是

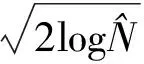
利用鲁棒中位数可以估计噪声的标准差，即

1.3 邻域小波系数法去噪

在阈值估计中采用邻域收缩的方法，可将小波系数分成非重叠的块，然后逐块与阈值进行比较。

设所取窗口小波系数的平方总和

其中B表示为所选领域窗口，dk,l表示待处理的小波系数。对于每个当前待处理的小波系数dk,l，需要考虑其邻域窗口B的尺寸大小。以收缩公式

(1)

处理图像中的小波系数，即得其估计值，其中k≥1且为整数。在NeighShrink法中，k取值为1。

在NeighShrink方法中，较大的阈值会遏制较多的噪声系数，因此，图像中的一些细节信息会丢失，重构图像时就会变得模糊。IIDMWT方法可克服这一问题，其收缩公式为[12]

其中0<α<1，如取α=3/4。

2 方法改进

考虑用指数函数控制小波系数的指数衰减，以适应尺度分解，为此将阈值修订为

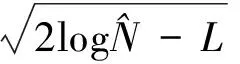
(2)

其中指数函数的调节因子

具体实现方法如下。

步骤1 对噪声图像实现二维离散小波变换，并且分解L层。

步骤2 对每个分解层的细节子带(HL,LH和HH),根据式(2)计算阈值，应用式(1)得到估计的小波系数。

步骤3 应用逆小波变换对修改后的小波系数进行重构，得到去噪后的估计图像。

3 实验结果及分析

实验采用3×3的邻域窗口，分别对灰度图像和彩色图像进行测试，其中灰度图像选取512×512的Lena和Hill，彩色图像选取512×512的Lena和Boat(图1)。采用峰值信噪比

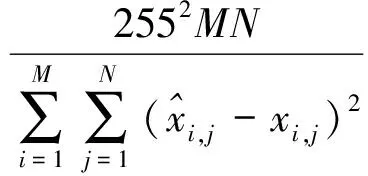
图1 实验用原始图像

3.1 灰度图像测试

对灰度图像添加不同级别标准差的高斯噪声，实验结果见图2和图3。

图2 σ=50时灰度图像Lena去噪效果

图3 σ=50时灰度图像Hill去噪效果

峰值信噪比对比情况如表1和表2所示。

表1 关于灰度图像Lena的峰值信噪比

σNeighShrinkIIDMWT改进方法1033．4633．6534．032030．4330．7631．083028．5728．9629．234027．2827．5627．855026．2126．4526．73

表2 关于灰度图像Hill的峰值信噪比

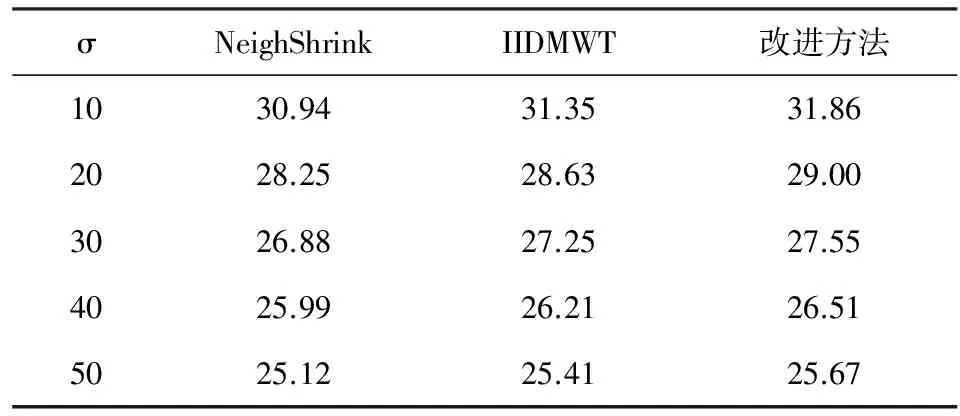
σNeighShrinkIIDMWT改进方法1030．9431．3531．862028．2528．6329．003026．8827．2527．554025．9926．2126．515025．1225．4125．67

3.2 彩色图像测试

对彩色图像添加不同级别标准差的高斯噪声，实验结果如图4和图5所示。

图4 σ=50时彩色图像Lena去噪效果

图5 σ=50时彩色图像Boat去噪效果

峰值信噪比对比情况，如表3和表4所示。

表3 关于彩色图像Lena的峰值信噪比

σNeighShrinkIIDMWT改进方法1030．5132．3533．082027．9929．9530．543026．6128．4928．864025．7327．2527．575025．0926．2326．51

表4 关于灰度图像Boat的峰值信噪比

σNeighShrinkIIDMWT改进方法1029．2732．3633．052026．0828．7229．213024．5126．8827．294023．4725．5025．985022．7324．6124．96

从实验结果所得诸表可见，随着高斯噪声强度的增强，改进方法相对NeighShrink和IIDMWT方法的峰值信噪比的值都有所提高。从图2和图3所示的测试结果也可看出，改进方法较好的保留了图像的边缘细节信息。改进方法与NeighShrink和IIDMWT相比较，既克服了在NeighShrink方法中信号的细节特征会过度平滑的问题，又改善了IIDMWT方法需要通过修改自适应阈值和收缩因子才可取得的效果，去噪效果在峰值信噪比和视觉外观上达到了相对较好的统一。

4 结束语

根据邻域小波系数的空间相关性对图像进行去噪，提出利用指数函数调节阈值的方式来适应尺度分解的小波系数。得到了较为满意的去噪效果，也能有效的去除图像中的强高斯噪声，达到相对较好的视觉外观。

[1] Graps A. An Introduction to Wavelets[J]. IEEE Computational Science and Engineering, 1995,2(2):50-61.

[2] 宋锦萍, 宋玲珍, 杨晓艺,等. 一种基于小波变换的图像消噪算法[J].电子与信息学报,2007,29 (1):43-46.

[3] 赵芹,林椹尠.一种新型的小波阈值图像去噪方法 [J].西安邮电学院学报,2012,17(6):56-59.

[4] Donoho D L, Johnstone I M. Ideal spatial adaptation via wavelet shrinkage[J]. Biometrika, 1994, 81(3): 425-455.

[5] Donoho D L, Johnstone I M. Adapting to Unknown Smoothness via Wavelet Shrinkage[J]. Journal of American Statistical Association, 1995,90:1200-1224.

[6] Donoho D L. De-Noising by Soft Thresholding[J]. IEEE Transactions on Information Theory, 1995, 41(3)：613-627.

[7] Chang S G, Yu B, Vetterli M. Adaptive wavelet thresholding for image denoising and compression[J].IEEE Transactions on Image Process,2000,9(9):1532-1546.

[8] Cai T, Silverman B. Incorporating information on neighboring coefficients into wavelet estimation[J]. Sankhya: The Indian Journal of Statistics,2001, 63(2): 127-148.

[9] Chen G Y, Bui T D. Multiwavelets Denoising Using Neighboring Coefficients[J]. IEEE Signal Processing Letters,2003, 10(7):211-214.

[10] Chen G Y, Bui T D, Krzyzak A. Image Denoising Using Neighbouring Wavelet Coefficients[C]//International Conference on Acoustics, Speech, and Signal Processing, 2004:917-920.

[11] Mohideen S K, Perumal S A, Sathik M M. Image De-noising using Discrete Wavelet transform[J]. International Journal of Computer Science and Network Security, 2008,8(1):213-216.

[12] Om H, Biswas M. An Improved Image Denoising Method based on Wavelet Thresholding(IIDMWT)[J]. Journal of Signal and Information Processing(USA),2012,3(1):109-116.

[责任编辑:孙书娜]

An improved threshold for image denoising based on neighboring wavelet cofficients

WU Chengmao1, HU Wei1, WANG Hui2

(1.School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China;
2. School of Automation, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

The NeighShrink cannot recover original image significantly because its threshold cannot adapt to the scale decomposition of wavelet coefficients obtained by the strength of the noise characteristics. In this paper, an improved threshold method is proposed. In this method, an adaptive denoising way of setting up the threshold of NeighShink is proposed to regulate threshold by matching the amplitude characteristic of wavelet coefficients with an exponential function. Experimental result show that the proposed method can retain the original image information much better after efficiently removing noise under different Gaussian noise intensity condition, and can obtain higher peak-to-signal noise ratio compared with NeighShrink and IIDMWT.

wavelet translate, threshold, neighbor wavelet coefficients, image denoising

10.13682/j.issn.2095-6533.2014.01.008

2013-09-09

陕西省教育厅科学研究专项基金资助项目(2013JK1129)

吴成茂(1968-)，男,高级工程师，从事图像处理研究。E-mail:wuchengmao123@sohu.com 胡伟(1987-)，男，硕士研究生，研究方向为多媒体信息处理。E-mail:huweiemail168@163.com

TP391.41

A

2095-6533(2014)01-0042-04