基于计数型控制图的设备预防维修控制

赵永强

(西安邮电大学 经济与管理学院, 陕西 西安 710121)

基于计数型控制图的设备预防维修控制

赵永强

(西安邮电大学 经济与管理学院, 陕西 西安 710121)

以设备零备件维修为研究对象，假设零备件的失效率服从指数分布，对零备件失效率进行参数估计。利用经济性模型确定控制图界限的参数，在参数已知的条件下，构建出零备件的计数型控制图模型，控制图可对设备零备件的失效频次进行有效预防控制。通过实例验证发现，可对设备零件的失效频次进行预防控制，识别零件失效是随机还是系统因素，使设备维修更有效。

计数型控制图；指数分布；定期预防维修；过程控制

设备的有效运行是保证企业正常生产的根本，良好的设备状态对企业产品质量保证、及时交货及降低运营成本而言十分重要。设备维修大致经历了事后维修、定期维修、预防维修等几个阶段。不论是预防置换还是定期预防维修，维修频率都会对维修质量产生影响。就定期预防维修而言，维修频率过高会产生过度维修的问题，维修频率较少又会影响到企业的产品过程质量。因此，既保证较少的维修次数，又能够保证维修质量是企业要解决的问题。

统计过程控制(Statistical Process Control， SPC)能高效、迅速地预测出非随机原因的发生及改变时间，以便及时采取措施进行改善，防止不合格品产生造成的不必要损失。随着自动化生产时代的来临，产品的生产效率大大提高，这就需要高的设备预防维修水平来保证高的产品质量，有效的设备预防维修策略也可以大幅度降低成本损失。因此，利用控制图来对设备的失效过程进行监控，及时提供预防维修信息就十分重要。

文[1]以设备的可靠性为目标，构建了设备平均故障间隔期的控制图模型。文[2]将均值-极差控制图应用到离合器的拉杆的预防维修控制中，案例显示可有效监控设备的维修过程。文[3]建立了基于均值极差控制图的轴承可靠性预防控制模型，根据对数据的分析，判断主轴是否存在故障，消除主轴早期系统故障，提高机床的可靠性。文[4]则研究了考虑预防维修成本及时间的过程控制图的经济性设计。文[5]考虑年龄置换策略下的均值控制图，以马尔科夫链为基础对模型进行拟合，找出最经济的控制图参数，并对其敏感性进行分析。文[6]研究了基于可靠性的过程控制图，给出了设备运行时间的控制图模型。

从以上研究可以看到，国内外利用控制图对设备维修进行预防控制的研究较少。一部分研究将控制图应用到了设备的预防维修，但考虑均值-极差控制图的角度；另一部分研究将维修策略作为总成本的一部分来探讨控制图的经济性，以均值控制图居多。若对零备件的失效情况利用控制图进行监控，就可以预测哪些失效是随机因素造成的，哪些是由于系统原因造成的，进而对设备失效的系统因素进行预防干预，这样就能够大幅度降低维修费用，节省企业的维修成本。一般的控制图是在3倍标准差的基础上建立的。从实际应用的角度来看，控制图的界限显然与被控制目标的质量特性有关，有的设备可靠性要求高，有的可靠性要求低，对控制图边界的要求就会有所不同，控制界限对成本有着直接的影响，如果都用3倍标准差作为上下界限，控制图的实际作用就不明显。因此，需要从经济性的角度考虑控制图的界限。本文以设备零备件失效次数为研究对象，假设零备件的失效率服从指数分布，对零备件失效密度函数进行参数估计。利用经济性模型确定控制图界限的参数。在参数已知的条件下，构建出零备件的计数型控制图模型，控制图可对设备零备件的失效频次进行有效预防控制。最后以实例验证该模型的有效性。

1 模型假设及参数

1.1 模型假设

设备的失效密度函数不同，控制图模型就不一样，构建模型前需要先假定一些约束条件，具体如下。

(1)设备零备件的失效服从指数分布；

(2)已知设备零备件的预防维修周期；

(3)在设备的工作时间内，设备零备件发生故障以后的维修方式为置换维修，不考虑维修成本的投入；

(4)预防周期内的故障处理时间很短，可以忽略不计其时间及成本；

(5)以机械设备为研究对象。

1.2 参数设定

假设设备零备件的故障分布函数服从指数分布，则其分布函数为[1]

F(t)=1-e-λt,

(1)

其中λ为未知参数。平均故障间隔时间(MeanTimeBetweenFailure，MTBF)是衡量一个产品(尤其是电器产品)的可靠性指标[7]。MTBF与λ的关系可表示为

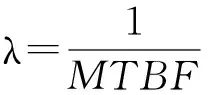
(2)

1.3 两类错误概率的确定

控制图可能出现两类错误。第一类错误是指过程本来正常，控制点却超出界外，发生误发警报的错误。把发生第一类错误的概率记为α。第二类错误是指过程已经出现异常，控制点仍在界内，发生漏发警报的错误。把发生第二类错误的概率记为β。将第一类错误造成的损失(停工损失、检查费用等)记为Cα，第二类错误造成的损失(不良品等)记为Cβ[8]，那么两类错误造成的总损失CZ则为

CZ=αCα+βCβ。

(3)

于是

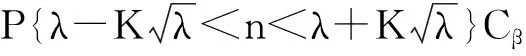
(4)

令CZ最小，即可求出K，进而求出α和β。

2 模型的构建

设备从时刻0开始工作，每逢故障就进行替换。替换的时间小到可以忽略不计。t为设备的运行时间，到时刻t发生故障的次数用概率变量N(t)表示。

到时刻t时发生n次故障的概率[9]为

Pn(t)=P{N(t)=n}。

(5)

P0(t)为设备在t时刻不发生故障的概率，它与故障分布函数之和为1，所以

P0(t)=e-λt。

(6)

当n≥1时，在t时刻内设备发生了n次故障。最初的故障发生时间间隔在(x,x+dx)内，随后在t-x时刻发生n-1次故障。首次发生的概率用故障时间的概率密度函数λe-λx表示，其余故障的概率用Pn-1(t-x)表示。若x的取值在0到t之间，则Pn(t)与Pn-1(t)间的关系为[10]

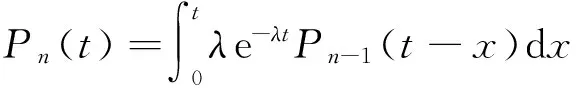
(7)

用式(7)计算P1(t)，则

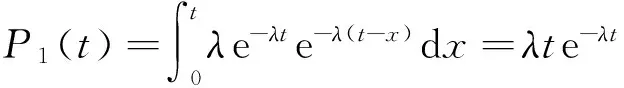
(8)

逐级推算，则

(9)

依据式(9)可以求得t时刻发生n次故障的概率为[11]

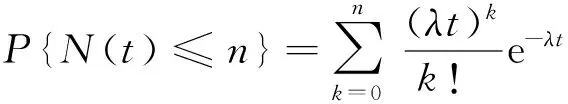
(10)

令α为控制图界限外的发生概率，计数型零备件控制图的上、下界限范围内的发生概率分别为

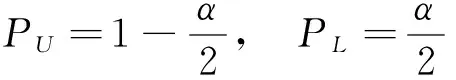
那么

(11)

3 实例分析

某纸箱生产企业，其工艺流程如图1所示。

图1 纸箱的生产工艺流程

对所有相关零部件的失效率进行统计，发现自动切割工艺的失效率达到51.324%，其他工艺设备失效率都在5%以下。因此，以自动切割工艺的零备件作为研究对象，通过对其以往平均故障间隔时间的计算，求得λ=0.05，该设备的预防维修周期为100小时。已知其发生两类错误的成本分别为

Cα=50元， Cβ=100元，

令CZ最小，将这两个参数带入到式(4)，计算得出K=3.17，则α为0.0015。将这些参数带入式(11)，得出控制图界限

nu=13, nl=0, ncl=5。

在预防维修周期内观测动切割工艺的零备件的失效次数如表1所示。

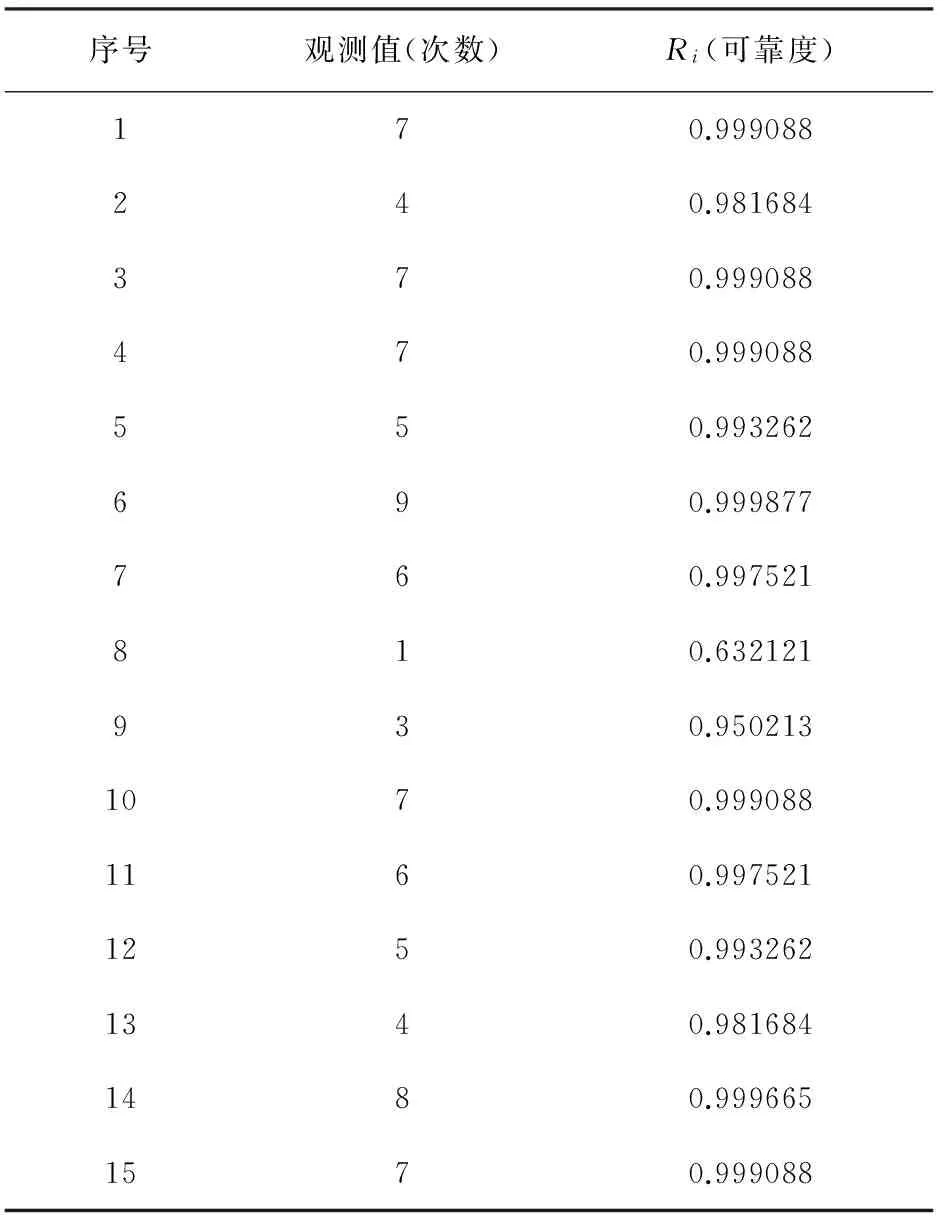
表1 自动切割工艺零备件失效数据及统计表

绘制出其控制图，如图2所示。

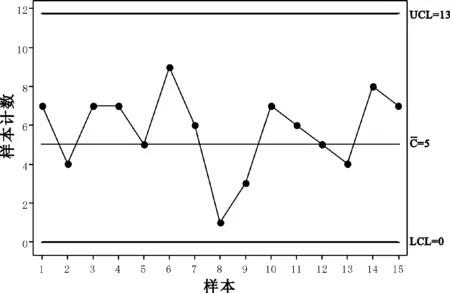
图2 自动切割工艺零备件的计数型控制图

由图2可以看到，所有控制点均在控制图界限以内，点子的分布都属于随机状态。在警戒区域不存在一侧连续两点的情况，依据通用控制图的判断标准对其进行判断可知，该零件的失效属于正常因素。如果发现有控制点出界或者以某种规律出现，由于在样本量较少时这类情况不应该发生，所以即可断定该零件的失效是由于系统因素造成的，企业随后从系统的角度去分析导致设备零部件失效的原因。由此可见，有效的使用控制图可以达到对设备失效过程的有效监控，帮助维修人员区分设备零部件失效的原因，减少了设备的过度维修成本。通过持续的控制图控制，逐渐消除设备零备件的失效的系统因素，就能够使设备的失效率大大下降，达到预防控制的目的。

4 结论

利用控制图的经济性模型计算出控制图上下界限的最优参数α、β。给出MTBF与λ的关系，以计数型控制图为基础，构建设备零备件的控制图模型。将控制图上、下界限参数α、β代入，求出设备失效次数的控制图界限。以实例验证了该模型的有效性。以纸箱生产流程为例，绘制出自动切割设备零部件失效的控制图，并依据控制图判断标准进行模型分析。通过持续的控制图控制，逐渐消除设备零备件失效的各个因素，就能够使设备的失效率大大下降，达到设备维修的预防控制目的。

[1] 周源泉.可修系统的可靠性控制图[J].质量与可靠性,2011(2)：10-13.

[2] 李爱民,陈亮,彭耀辉.控制图在装备维修质量控制中的应用[J].四川兵工学报,2009,30(1):58-60.

[3] 周广文,贾亚洲,刘君义.专用数控机床主轴早期可靠性控制图分析[J].2005(3):37-39.

[4] Haworth D A. Regression control charts to manage software maintenance [J].Journal of Software Maintenance and Evolution: Research and Practice, 1996, 8(1):35-48.

[5] Yeunga T G., Cassady C R.Simultaneous optimization of X control chart and age-based preventive maintenance policies under an economic objective [J]. IIE Transactions, 2007, 42(2):145-159.

[6] Lee B H, Rahim M A. An integrated economic design model for quality control, replacement and maintenance [J]. Quality Engineering, 2004, 13(4): 581-593.

[7] 孙静.接近零不合格过程的质量控制[M],北京:清华大学出版社, 2001:41-45.

[8] Linderman K, McKone-Sweet K E, Anderson J C. An integrated systems approach to process control and maintenance [J]. European Journal of Operational Research, 2005, 164(2): 324-340.

[9] Panagiotidou S, Nenes G. An economically designed, integrated quality and maintenance model using an adaptive Shewhart chart [J]. Reliability Engineering & System Safety, 2009, 94(3): 732-741.

[10] Steiner S H. Mackay R J. Monitoring processes with data censored owing to competing risks by using exponentially weighted moving average control charts [J]. Applied Statistics, 2001, 50(3):293-302.

[11] Cassady C R, Bowden R O, Liew L,Pohl E A. Combining preventive maintenance and statistical process control: a preliminary investigation [J].IIE Transactions, 2000, 32(6):471-478

[责任编辑:祝剑]

Equipment preventive maintenance control model based on attribute control charts

ZHAO Yongqiang

(School of Economics and Management, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

By taking spare parts maintenance of equipment as the research object and assuming the equipment failure density function obeying exponential distribution, the failure rates of spare parts is calculated by parameter estimation. The parameters of control chart line is calculated based on the economic model, and the attributes chart model of spare part is constructed on the condition of parameters be given. Therefore, this control chart can monitor equipment spare parts failure frequency effectively. Example testing result shows that the random or systematic factors of equipment parts failure frequency can be identified by this control chart, which is effective to equipment repair.

attributes control chart, exponential distribution, periodic preventive maintenance, process control

10.13682/j.issn.2095-6533.2014.06.018

2014-03-12

航空科学基金资助项目(20130753007)；西安邮电大学青年教师科研基金资助项目(ZL2012-28)

赵永强(1976-)，男，博士，副教授，从事工业工程方向研究。E-mail：zhaoyq1220@xupt.edu.cn

TH17

A

2095-6533(2014)06-0092-04