高精度工作台速度反向时摩擦补偿研究*
2014-07-18罗石丰郭锐锋王志成
罗石丰 ,郭锐锋 ,王志成
(1.中国科学院大学,北京 100049;2.中国科学院 沈阳计算技术研究所,沈阳 110168)
高精度工作台速度反向时摩擦补偿研究*
罗石丰1,2,郭锐锋2,王志成2
(1.中国科学院大学,北京 100049;2.中国科学院 沈阳计算技术研究所,沈阳 110168)
在消除了丝杠导程、间隙等误差之后,进给系统中存在的摩擦是影响工作台运动控制精度的主要因素。由于摩擦的影响,导致工作台速度反向时产生爬行现象,从而使得误差突然增大。文章对摩擦误差产生机理和补偿方法进行了研究,从瞬态响应的视角揭示了摩擦误差产生的机理,通过数学推导精确计算出爬行现象的持续时间,以及由此导致的最大跟随误差。提出了一种零速对称式摩擦补偿方法,该方法在工作台的爬行时间内进行补偿,使工作台尽快脱离爬行状态,仿真结果表明该方法能够显著的减小爬行时间。
摩擦补偿;高精度工作台;爬行现象
0 引言
进给伺服系统是数控系统的重要组成部分,在很大程度上决定了数控系统的加工精度、表面质量和生产效率。
摩擦是引起高速、高精度数控机床进给伺服机构轮廓误差的主要因素之一,摩擦有害于运动精度的控制,并在低速时表现出很强的非线性特征[1]。数控机床的摩擦现象主要出现在速度过零时,由于非线性摩擦力的作用使数控系统无法通过控制器来完全消除由摩擦带来的不利影响,机床运动轴的跟随误差会出现尖峰现象,导致轮廓精度变差[2]。因此,摩擦成为阻碍进一步提高伺服系统控制精度的重要因素。
为了减少摩擦的负面影响,可以采取某种控制策略来减少摩擦所产生的误差,但更多的是采用摩擦补偿的方法。摩擦补偿的方法有很多种,文献[3-4]对其进行了总结。本文研究的对象是一种采用闭环控制的高速高精度伺服进给工作台。文献[5]根据两维混合摩擦模型预测摩擦,进行前馈补偿,取得了较好的效果。文献[6]把预先测量到的摩擦误差,作为补偿指令加入到位置指令中进行补偿。文献[7]采用GMS模型加干扰观测器进行摩擦补偿。但是这些方法都比较复杂,不易于实现。本文通过分析工作台速度反向时的摩擦特性,提出了一种便于工程实现的零速对称式摩擦补偿方法,以期使工作台尽快脱离爬行状态,减小摩擦误差。
1 反向时摩擦力分析
在机械伺服系统中,具有相对运动或相对运动趋势的两个接触面上会产生摩擦力。接触面由相对静止到相对运动经过4个阶段:静摩擦阶段(预滑动阶段),边界润滑阶段,部分液体润滑阶段以及完全液体润滑阶段。而这4个阶段又可以概括为预滑动阶段和滑动阶段(后3个阶段)。在静摩擦阶段,摩擦力不依赖于速度,它实际可以认为是由弹性形变所产生的,从控制的角度看,正是这种弹性变形导致了增加的静摩擦力。这种弹性变形称之为“滑前位移”。

图1 鬃毛模型
为了克服摩擦给伺服系统带来的危害,提高伺服系统的性能,研究人员建立了很多反映摩擦现象的模型。其中C.Canudas de Wit提出了一种LuGre模型[8],如图1所示。该模型认为两个接触表面之间有很多不规则的接触点,而这些接触点可以当做弹性鬃毛。当施加不超过最大静摩擦力的外力时,鬃毛发生形变,从而在两个接触表面之间产生相对位移,此时相对位移可以认为是鬃毛的形变量。速度反向时,摩擦力处于静摩擦阶段,驱动力小于最大静摩擦力。此时摩擦力表现出弹性行为,与鬃毛的平均形变成正比。当驱动力大于最大静摩擦力时,鬃毛发生完全形变,并且物体开始滑动,此时摩擦力与速度有关。
对于高精度伺服工作台而言,在消除了丝杠导程,间隙等误差之后,进给系统中存在的摩擦就成为了影响工作台运动控制精度的主要原因。当伺服工作台速度反向时,由于静摩擦的影响,系统容易出现运动不平稳或不稳定的爬行现象。爬行现象是指机床的运动部件在低速或重载运动的情况下,出现的时快时慢或时走时停的不均匀运动现象,也称为粘滑运动。爬行现象如图2,图3所示,工作台出现爬行时,将严重影响机床的定位精度以及加工工件的表面质量。图3中红色曲线是给定速度,黄色曲线是实际速度。
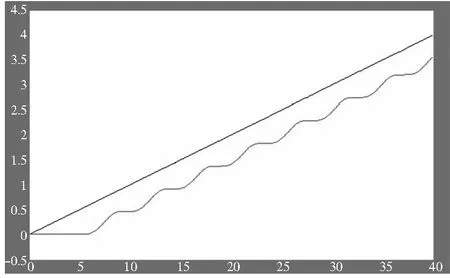
图2 爬行现象
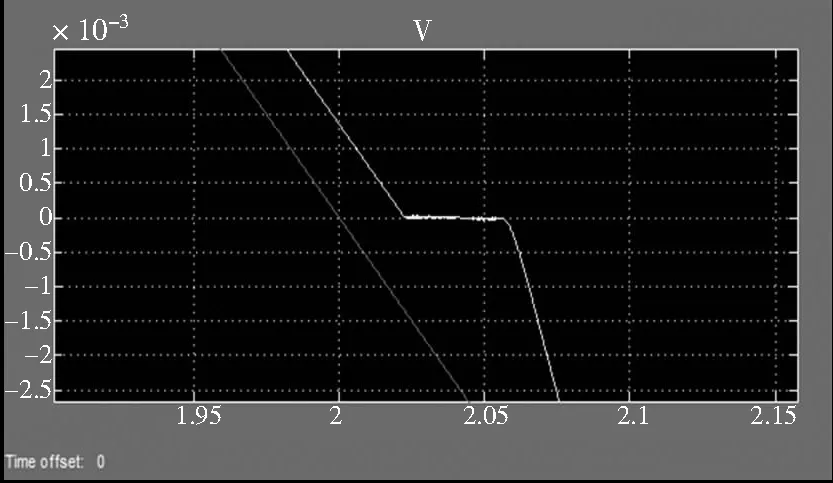
图3 工作台爬行
2 摩擦补偿方法
2.1 爬行现象持续时间
为了补偿速度反向时的摩擦,抑制爬行现象,我们需要知道工作台处于爬行现象的时间。现假设工作台速度为零的时刻为T0,而误差最大时刻为T1(工作台脱离爬行现象时刻),在这期间,工作台处于预滑动阶段,令χb为T0到T1期间的相对位移(即鬃毛形变量)。又由于这个时间很短,可以假设加速度为常数α,则:
(1)
根据Dahl模型[9],可得:
(2)
其中Fc为库伦摩擦力,σ为刚度系数。
令ΔT为工作台处于预滑动阶段的时间(T1-T0),则:
(3)
可得:
(4)
2.2 零速对称式摩擦补偿方法
抑制工作台的爬行现象,提高工作台的精度,我们只需要在工作台的预滑动阶段,也就是速度为零的时候进行摩擦补偿。因而速度不为零时,摩擦补偿为0,根据上述所得,摩擦补偿如下:
(5)

(6)
摩擦力模型如图4所示:

图4 摩擦力模型

综上所述,可得零速对称式摩擦补偿方法为:
Ffric=
3 仿真实验及分析
进给伺服系统的仿真方框图如图5所示:

图5 进给伺服系统方框图
其中Kpp为位置环增益(50000),
Kvp为速度环增益(40),
Kcp为电流环增益(2),
L为电动机电感(52.7mH),
Rm为电动机电阻(1.04Ω),
Ke为电机反电动势(0.18V·s/rad),
Kt为电动机转矩常数(0.82N·m/A),
J为对电机转动惯量(0.00299kg·m2),
Kbs为丝杠导程(1.59mm/rad),
K为丝杠刚度(410000N/m),
m为工作台质量(48.8kg),
B为工作台阻尼(15000N·s/m),
Ff为摩擦力(N)。
摩擦力采用了Stribeck模型,Fc为18.9272N,Fs为26.9487N,Vs为0.0172m/s,B为56.6223N·s/m。我们假设丝杠导程,间隙等误差已经消除,只针对工作台上的摩擦进行补偿。根据上述摩擦补偿方法,在Matlab的simulink模块中进行仿真实验。给定速度为v=0.01·sin(πt),所得实验结果如图6。

图6 补偿前后速度曲线对比图

图7 补偿前后位置误差曲线对比图
图6中深色曲线为给定速度,上边浅色曲线为补偿前工作台速度曲线,下边浅色曲线为补偿后的。图7中上边曲线为补偿前位置误差曲线,下边曲线为补偿后的。可以看出在速度反向时(1s),由于摩擦的影响,导致工作台出现爬行现象,从而导致该时刻位置误差突然增大。而补偿后,该时刻的位置误差显著减小,取得了很好的效果。通过图6可以发现,补偿前,工作台处于爬行现象的时间为0.05s,而补偿后,爬行时间为0.02s,显著减小。因此零速对称式摩擦补偿方法能有效的抑制低速时工作台的爬行现象,减少工作台处于爬行现象的时间,取得较好的系统低速控制特性。
4 结论
(1)从瞬态响应的视角揭示了摩擦误差的产生机理,并精确计算出爬行现象的持续时间。
(2)工作台速度反向时的误差,主要是由摩擦导致的爬行现象引起的。
(3)提出的零速对称式摩擦补偿方法显著地减小了工作台处于爬行现象的时间,基本消除了工作台在速度反向时由摩擦造成的误差。
[1] Armstrong Helouvry B. Strick-slip and control in low-speed motion[J]. IEEE Trans. on Auto. Control,1993,38(10)∶1483-1496.
[2] LIU Dong,MEI Xuesong,FENG Bin,etal.The Simulation of Dynamic Characteristics for the Ballscrew Servo Feed Drives in NC Machine Tool[C]//CIRP-2ndInternational Conference Process Machine Interactions,2010.
[3] Brian Armstrong Helouvry, Pierre Dupont, et al. A survey of models, analysis tools and compensation methods for the control of machines with friction[J]. Automatic, 1994,30(7):1083-1138.
[4] 刘强,尔联洁,刘金琨.摩擦非线性环节的特性、建模与控制补偿综述[J].系统工程与电子技术,2002,24(11) : 45-53.
[5] 梅雪松,陶涛,堤正臣,等.高速、高精度数控伺服工作台摩擦误差的研究[J].机械工程学报,2001,37(6):76-81.
[6] Tung E D, Anwar G, Tomizuka M. Low velocity friction compensation and feedforward solution based on repetitivecontrol. ASME Journal of Dynamic Systems, Measurement and Control, 1993,115(2)∶279-284.
[7] Zamberi Jamaludin, Hendrik Van Brussel, and Jan Swevers。Friction Compensation of an XY Feed Table UsingFriction-Model-Based Feedforward and an Inverse-Model-Based Disturbance Observer[J]. IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS,2009,56(10):3848-3853.
[8] C.Canudas de Wit, H.Olsson, K.J.Astrom and P.Lischinsky. A new model for control of systems with friction[J].IEEE Transactions on Automatic Control, 1995, 40(3): 419-425.
[9] P. Dahl. A solid friction model[J]. Aerospace Corp.,El Segundo,CA,Tech. Rep. TOR-0158 (3107-18), 1968.
(编辑 赵蓉)
The Research of Friction Compensation of High Precision Table at Velocity Reversal
LUO Shi-feng1,2,GUO Rui-feng2,WANG Zhi-cheng2
(1.University of Chinese academy of sciences,Beijing 100049,China;2.Shenyang institute of computing technology,Chinese academy of sciences,Shenyang 110168,China)
After eliminating the leadscrew lead and backlash,existing in the feeding system of friction is the main factor that affected the accuracy of motion control of table. Due to the influence of friction,the table gets crawl phenomenon when it’s at velocity reversal,so as to make the error increases suddenly.This article studies the mechanism of friction error and compensation methods,revealing the mechanism of friction error by the Angle of transient response and through mathematical derivation accurate calculate the duration of the crawling phenomenon,and the resulting in the largest follow error.A symmetric zero velocity friction compensation method is proposed,used at the crawling time of table to get table out of crawl state as soon as possible,and the simulation results show that this method can significantly reduce the crawl time.
friction compensation;high precision worktable;the crawling phenomenon
1001-2265(2014)06-0001-03
10.13462/j.cnki.mmtamt.2014.06.001
2013-10-06;
2013-10-22
核高基国家科技重大专项(2012ZX01029001-002)
罗石丰(1990—),男,湖南娄底人,中国科学院大学,中科院沈阳计算技术研究所硕士研究生,研究方向为嵌入式与数控技术,(E-mail)yuye_tingsheng@163.com;郭锐锋(1968—),男,沈阳人,中科院沈阳计算技术研究所博士生导师,研究员,研究方向为实时系统,数控技术。
TH166;TG65
A
