全自动平衡修正设备中测试单元的隔振方法研究*

蒋 力，顾超华，曾 胜，罗迪威，金 涛

(浙江大学 化工机械研究所，杭州 310027)

全自动平衡修正设备中测试单元的隔振方法研究*

蒋 力，顾超华，曾 胜，罗迪威，金 涛

(浙江大学 化工机械研究所，杭州 310027)

以全自动平衡修正设备为对象，研究了其中的测试单元在有冲击干扰情况下的隔振方法。分析和测试了设备的整机动力特性，由此设计了不平衡量测试单元的柔性隔振装置，对测试单元的动态工作过程进行了运动建模。在模型的基础上进行了模拟计算，分析了测试单元在有无隔振装置时对外界冲击干扰的响应。实验表明，设计的柔性隔振装置可有效抑制冲击干扰，从而提升不平衡量测量的快速性和测量精度。

不平衡量；修正；测试单元；瞬态响应

0 引言

批量生产的转子如电机转子，由于设计、材质不均匀以及制造安装等原因，往往存在较大初始不平衡量。当转子高速旋转时，过大的不平衡量会产生一个周期的激振力，从而引起振动和噪音[1-2]，因此必须对转子进行动平衡，使其达到一定的标准。一般的手工动平衡不适应现代化批量生产的要求，全自动平衡修正设备便应运而生[3-5]。

不平衡量精确快速测量是全自动平衡修正设备高效运行的前提。目前通用平衡测试机是非常成熟的产品，可以达到很高的测量精度，但它却不适合全自动平衡修正设备。原因是通用平衡测试要求有非常安静的物理平台，且对测量的快速性不作要求，可以用加长测量时间的方法来换取测量精度[6]。再者全自动平衡修正设备中有搬运机械手和去重单元等运动部件，所产生的瞬态冲击会影响不平衡量的测量时间和精度。文献[7]设计了一种滤波器，可有效减低测量时间和提高测量精度，但对瞬态冲击产生干扰的削弱有限。为此可从设备的整机动力学出发，研究可行的减振和隔振方法。

佀国宁等[8]采用有限元软件建立了整机的柔性体动力学模型，对其进行了动力学求解，分析了运动误差和速度变化规律，这为研究整机的动态性能提供了重要的理论依据。Uttara等[9]将整机结构分为几个子结构，分别构造各自的动力学方程，再利用变形协调条件得到整机的动力学模型，为结构耦合复杂时变系统的快速预估奠定理论基础。

从动力学角度研究提高动态的不平衡量精确快速测量的方法。分析和测试了设备的关键模态，设计了测试单元的隔振装置，建立了测试单元的运动方程。模拟了测试单元的瞬态响应情况，最后通过实验进行了验证。

1 问题的提出

全自动平衡修正设备中，当测试单元单独运行，仅测量不平衡量且取24采样周期时，可以达到日本同类机器“幅值3mg相位2度”的重复测量精度[7]。当整机正常运行，即不但测量而且搬运和去重时，测试单元的重复测量精度恶化为“幅值8mg相位4度”以上，这表明机械手和去重单元会对测试单元的测量过程产生干扰。由于测试单元、机械手及去重单元都安装在同一底板上，因而有必要分析包含各部件在内的底板的动力学特性。

利用ANSYS有限元软件，对某定型的全自动平衡设备的底板进行建模，其中的各测试单元、机械手和去重单元，由于本身刚性足够好，所以都简化为附加质量，平均分布在各自与底板连接的螺钉位置。图1a为有限元模型，通过分析计算可知底板的一阶固有频率为30Hz左右，其模态为对称弓形(见图1a)。这说明垂直运动的机械手可能会对安放在底板上的测试单元产生水平方向的冲击干扰。图1b为设备底板在机械手上下动作时，在测试单元中水平放置的测振传感器，输出的浮块的振动信号的频谱分析。可以看出底板确实存在30Hz的固有频率。测试单元中转子工件的转速一般取为25～35Hz，这样底板的固有频率将会对测试单元的测量造成干扰。

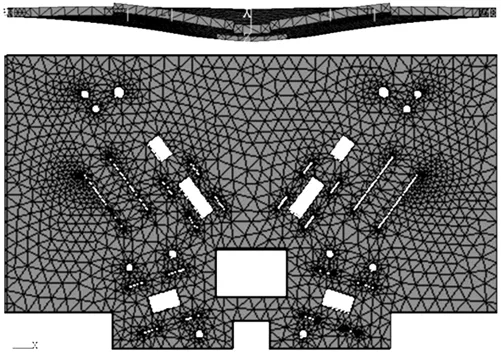
(a) 包含所有部件的整机有限元模型

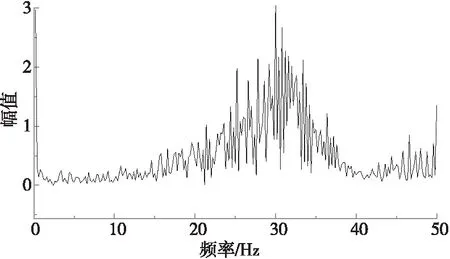
(b) 底板冲击频谱分析图1 整机动力学分析

2 隔振装置设计

为解决运动部件对测试的冲击干扰问题，有多种可行的方法。一种是将底板加厚以提高底板的固有频率。目前的底板已经达到了35mm的厚度，再增加厚度，整机材料及加工成本将提高，且整机过重，不利于安装调试和运输。另一种方法是在测试单元与底板间加装隔振装置，利用橡胶材料提供的弹性与阻尼，阻断底板振动对测试单元的干扰。加装隔振装置的测试单元如图2所示：测试单元的结构与普通软支撑平衡测试无差别，即由皮带9驱动的转子工件1通过两只90度V形架8支撑在两只浮块3和10上，每只浮块通过柔性簧片2支撑在机架上，水平安装在机架5上的两只传感器4通过测量两只浮块的振动，换算得到转子工件的不平衡量。在测试单元底板的四个边角附近，增加四只“中”字型聚氨酯柔性支撑6，连接到设备大底板7。图2c为隔振装置的安装示意图，图2b为加装隔振装置的正常状态，图2a为隔振装置的局部剖视图。通过改变图2a中聚氨酯柔性支撑的尺寸D和d就可改变隔振装置的支撑刚度，从而改变隔振固有频率和隔振效果。必须指出，传统的气囊型隔振器[10]，体积太大，不容易安装到测试单元上，所以不能选用。

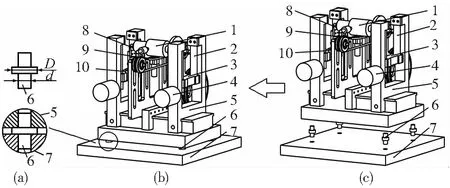
1.转子工件 2.簧片 3.左浮块 4.传感器 5.机架 6.聚氨酯柔性支撑 7.设备大底板 8. V形架 9.皮带 10.右浮块

图2 测试单元加装隔振装置后的结构示意图

由图1b底板冲击频谱可知，底板产生的激励约为30Hz，隔振装置应使其固有频率远低于30Hz[10]。这可通过减小图2中的尺寸D和d以降低刚度来实现。注意到，过低的固有频率会使尺寸D和d以过小，使测试单元不够稳固扎实。经过反复比较和实验，当D=14mm和d=10mm时，隔振橡胶支撑的测试单元的固有频率为5Hz，约为底板激励频率的1/6，既满足隔振要求也使测试单元足够稳固扎实。这时隔振装置提供的支撑刚度约为2.3e4 N/m。

3 运动方程

图2中的测试单元可简化为图3所示的计算模型。图3中的转子工件、左浮块、右浮块、机架和底板分别定义为物体0～4，各物理量，如质量m、惯量I/G、刚度k、阻尼c、位移x和摆动角位移θ的标记遵循以下原则：Pi表示第i个物体的P(绝对)物理量，Qij表示第i个和第j个物体的Q物理量。如m3为机架质量，k13和c13分别为左浮块与机架间的刚度和阻尼。

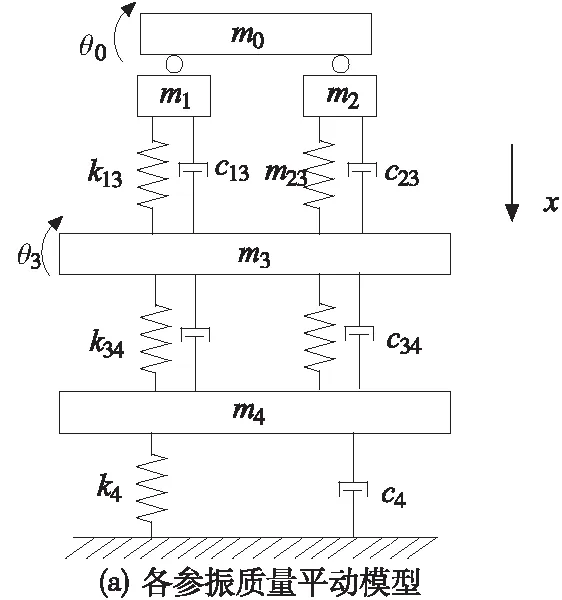
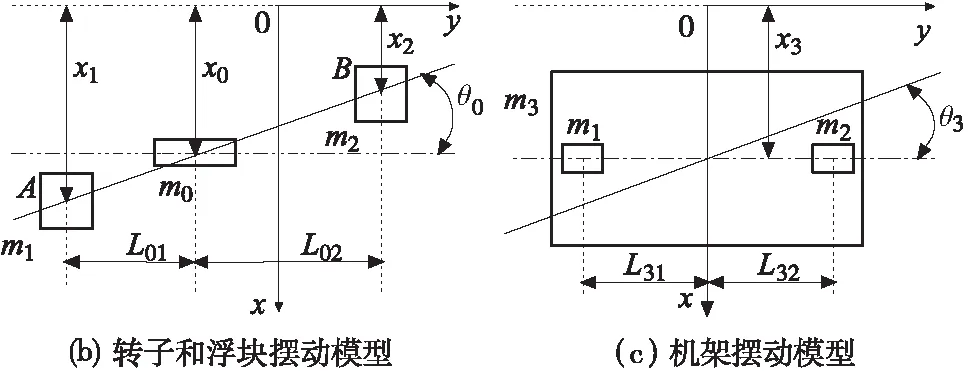
图3 计算模型

图3a为测试单元平动简化模型，转子工件m0、左浮块m1、右浮块m2、机架m3和底板m4都简化为集中质量，其中转子工件存在水平平动x0和水平摆动θ0。转子工件通过铰链的形式，与左浮块m1和右浮块m2连接，左浮块和右浮块被板簧限制，只有平动x1和x2。机架m3通过四只聚氨酯柔性支撑与底板m4连接，所以机架m3不但有平动x3，还有摆动θ3；图3b为转子工件水平摆动模型，图中L01和L02分别为转子工件质心到左右两浮块的距离；图3c为机架水平摆动模型，图中L31和L32分别为机架质心到左右两浮块的距离。

对转子工件的平动和摆动，分别有运动方程

m0e0Aω2sin(ωt)+m0e0Bω2sin(ωt+φ)-f01-f02

(1)

-m0e0Bω2sin(ωt+φ)L0B

(2)

式中e0A和e0B分别为转子工件两校正面上的初始偏心，L0A和L0B分别为转子工件两校正面距质心距离。

对左右浮块，有运动方程

(3)

(4)

转子工件、左右浮块之间的相对位移关系为

x1=x0+θ0L01

(5)

x2=x0-θ0L02

(6)

机架的平动和摆动方程为

(7)

(8)

最后，对于底板有

(9)

式中F(t)为外界作用在底板上的冲击力。

式(1)～(9)即为描述转子工件在平衡测试单元中的运动微分方程组，利用该方程组，既可以考察当F(t)=0时，左右浮块测试点x1和x2在转子不平衡量e0A和e0B作用下的响应情况，还可考察F(t)为冲击力时，x1和x2的响应情况。

4 测试单元瞬态响应模拟

方程(1)～(9)为多变量二阶线性微分方程组，求解解析解存在困难，故可用Runge-Kutta法进行数值求解。求解的初始条件为静止且初始位移为零，当方程(1)～(9)达到稳态后加入冲击，考察此时瞬态响应。为了使数值解与实验结果对照，方程(1)～(9)中参数的取值与后续实验对象的参数一致。表1给出了测试单元各种参数的描述及数值。表中的质量和惯量由UG实体建模或实际称重得到，刚度值由有限元建模或通过固有频率测试后换算得到，阻尼值由实际单体冲击响应衰减曲线计算得到。

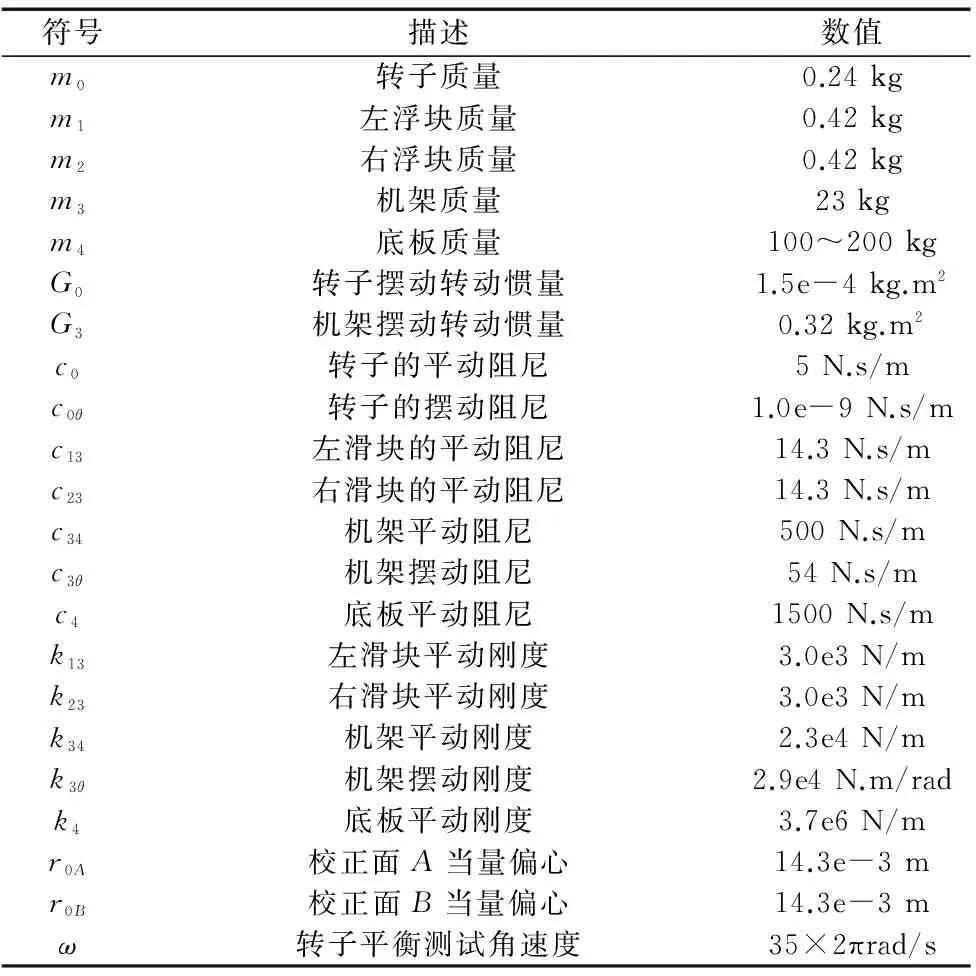
表1 参数描述及数值

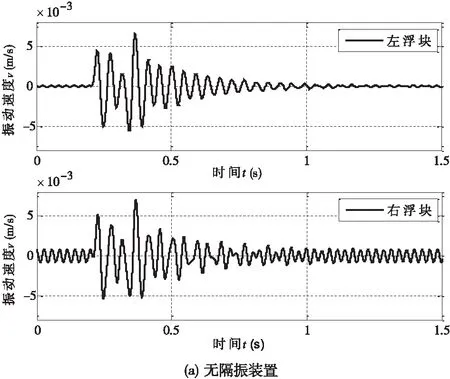
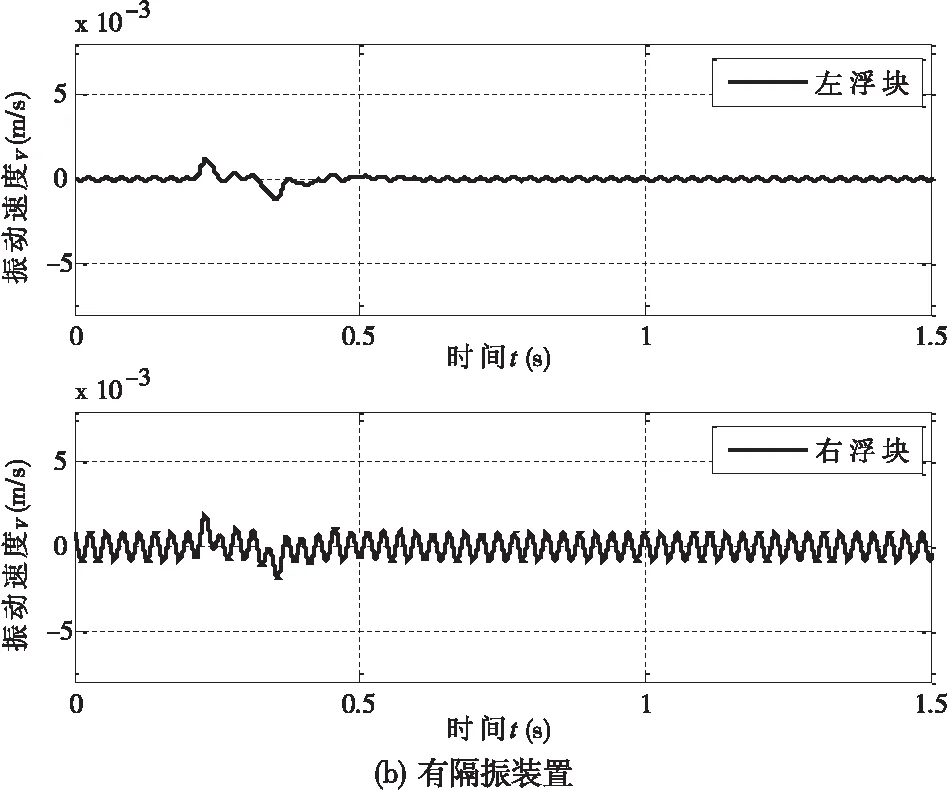
图4 测试单元受冲击后的瞬态响应模拟结果

需要指出的是，参数k34为隔振装置提供的支撑刚度，其实测值为2.3e4 N/m。模拟计算中当刚度k34取值为2.3e4 N/m时，为有隔振装置；当k34取为很大值时，为无隔振装置。

将冲击力加载在底板m4上，对有无隔振装置的两种情况进行瞬态响应计算，测量点即浮块m1和m2的响应结果如图4所示。由于测试单元采用的是振动速度传感器，故图4示出的是浮块的振动速度v1和v2。

从图4所示的计算结果看，无隔振装置情况下，当底板受到冲击后，其瞬态响应将会传到测试单元的测量点，即左右浮块，对测量结果造成影响，使测量的重复性变差。在有隔振装置时，隔振装置对冲击起到了良好的抑制作用，提高了冲击环境下的信噪比。

图5 实验测试单元

5 实验验证

为了验证隔振装置的实际效果，进行实验，测试单元如图5所示。

5.1 瞬态冲击实验

实验中为了保证测试的重复性和可比较性，在气压一定的情况下，使气动机械手连续上下动作，对底板形成冲击，以干扰测试单元。振动数据的采集点为测试单元中感应左右浮块的磁电速度传感器输出。在有无隔振装置时，采集到的振动速度信号如图6所示。

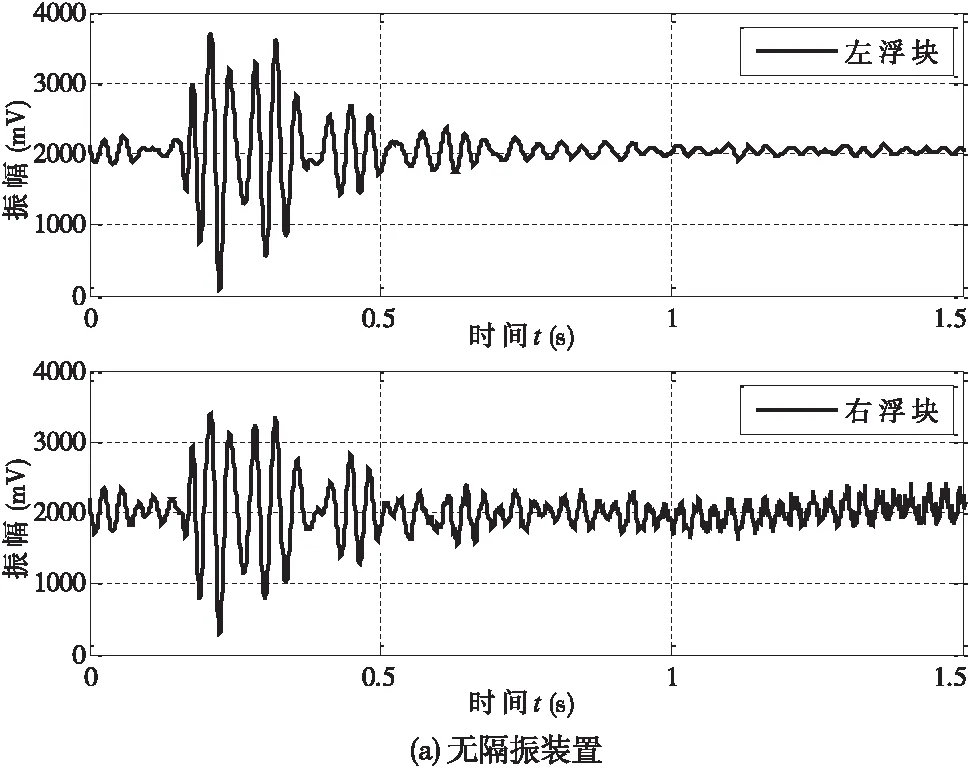
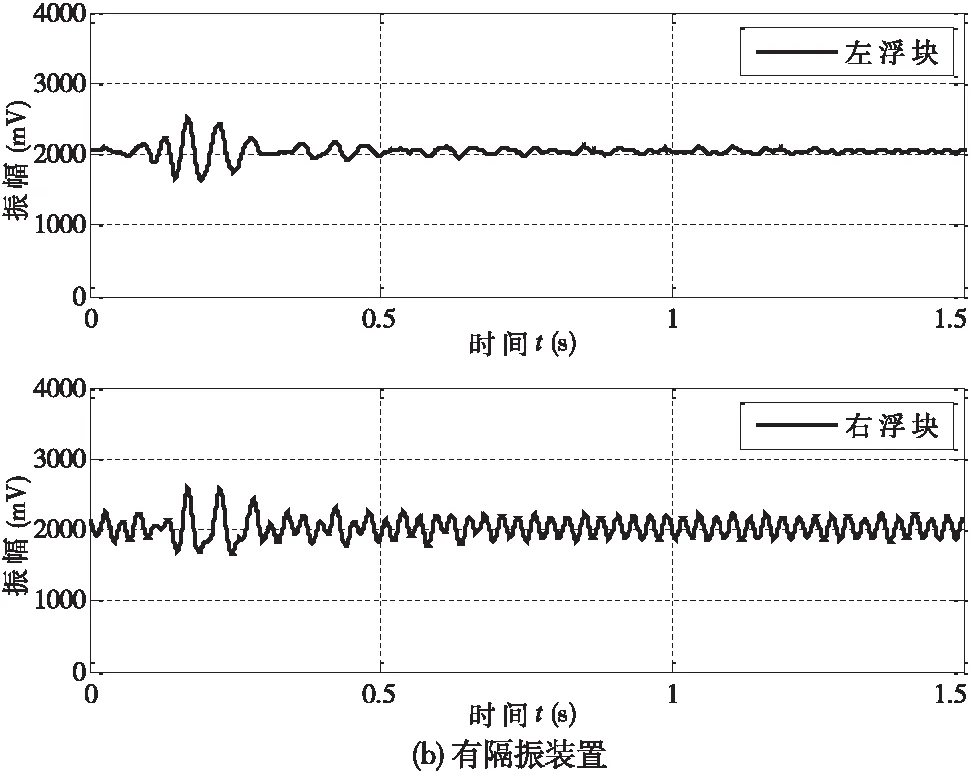
图6 测试单元受冲击后的瞬态响应测试结果

图6中，对比有无隔震装置时测点在冲击环境下的响应表明，实验中设计的隔振装置具有很好的隔振效果，能将绝大部分外来干扰滤除。比较图6的实际测试数据和图4的模拟计算结果，可以看出，它们相似度非常高，这说明式(1)～(9)可以很好地描述测试单元的运动过程。

5.2 动态重复性实验

任选一转子工件，其初始不平衡量为178mg。仍以机械手运动为冲击，在无隔振无冲击、无隔振有连续冲击和有隔振有连续冲击三种情况下，进行不平衡量测试，记录的实验数据如表2所示。表2数据表明在无隔振无冲击的情况下，测试单元不平衡量重复测量精度为“幅值3mg相位2度”，测量时间小于5s，重复精度和测量速度较好。当加入机械手冲击时，重复测量精度恶化到了“幅值8mg相位4度”，且测量时间都大于5s。加入隔振装置后，重复测量精度和测量速度都分别回到“幅值3mg相位2度”和5s以下，这表明设计的隔振装置具有很好的隔振效果。

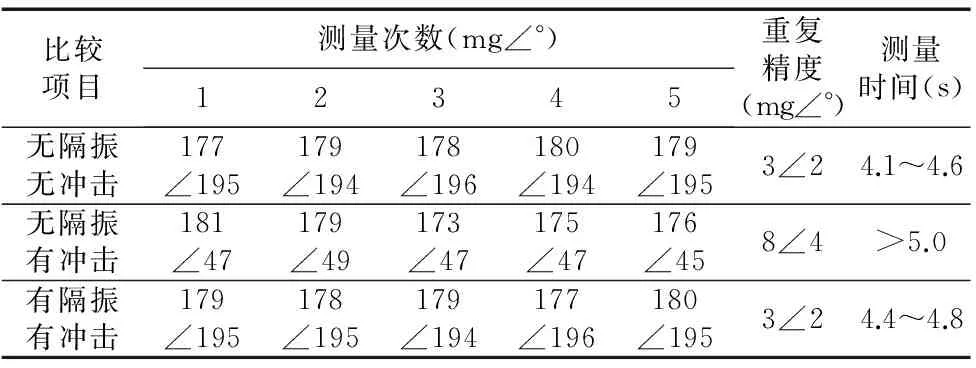
表2 各种情况下的不平衡量测试数据

6 结束语

分析了全自动平衡设备的整机动力特性，建立了不平衡量测试单元的动力学模型，模拟了动态工作过程，设计了测试单元的隔振装置，通过实验验证了隔振装置的减振作用，使其在有连续冲击干扰的情况下达到了重复测量精度“幅值3mg相位2度”且测量时间小于5秒/次的测量水平。文中的隔振方法可为机床中需要局部隔振的场合提供设计参考。

[1] 刘美生，王蛟茹，姜爱军，等. 动不平衡及车轮动平衡机不平衡量的测量[J].中国测试技术,2003,29(3):3-6.

[2] 任海军，贺利乐. 机械设备转子不平衡的诊断与平衡[J]. 煤矿机械, 2007, 28(7): 176-178.

[3] 康成良，李慧敏，赵良梁，等. 用于中小型电机转子的全自动平衡机的设计与实现[J].组合机床与自动化加工技术. 2007(2)：67-70.

[4] 康成良，曾胜，赵良梁，等. 全自动平衡机控制系统中多机通讯的设计与实现[J].组合机床与自动化加工技术,2008(4):53-56.

[5] 李常品，曾胜，康成良，等. 四工位全自动转子平衡机的设计与实现[J].制造技术与机床,2008(12): 89-92.

[6] 曾胜,汪希萱,李元涌.小速差双转子系统不平衡矢量识别方法的研究[J].振动工程学报,1996,9(4):399-404.

[7] 曾胜,任意,李常品，等. 一种可实现不平衡量快速测试的带通滤波器[J].振动与冲击, 2011,30(6):36-40,66.

[8] 佀国宁,杨建新,余跃庆，等.多轴联动龙门式加工中心整机动力学研究[J].组合机床与自动化加工技术,2009 (11): 55-59.

[9] Uttara V. Kumar,Tony L. Schmitz. Spindle dynamics identification for Receptance Coupling Substructure Analysis[J]. Precision Engineering, 2012, 36(3):435-443.

[10] 朱石坚，楼京俊,何其伟,等. 振动理论与隔振技术[M]. 北京:国防工业出版社, 2006.

(编辑 李秀敏)

Study of Vibration Isolation Method for Test Unit in Automatic Balancing Correction Machine

JIANG Li, GU Chao-hua, ZENG Sheng, LUO Di-wei ,JIN Tao

(Institute of Chemical Machinery, Zhejiang University, Hangzhou 310027)

Taking the automatic balancing correction machine as the object, the vibration isolation method in a shock jamming environment is studied. Based on the analysis and the test of the dynamics of the whole machine, the flexible vibration isolation device (FVID) is designed. The equation group that describes the full motion process of the test unit is built up, based on which the simulation calculations of the transient response of the test unit to the outside shock are performed. The experimental data proves that the designed FVID can work effectively to suppress the shock disturbance hence improve the rapidity and the accuracy of the unbalance measurement.

unbalance;correction;test unit;transient response

1001-2265(2014)07-0084-04

10.13462/j.cnki.mmtamt.2014.07.023

2013-10-22；

2013-11-20

浙江省重大科技专项资助(2011C11064)

蒋力(1987—)，男，杭州人，浙江大学硕士研究生，从事全自动平衡修正技术研究，(E-mail)jianglicool@zju.cn;通讯作者：顾超华(1962—)，男，杭州人，浙江大学副教授，从事全自动平衡修正技术研究。

TH166;TG65

A