基于PSO-BP神经网络和Hilbert谱奇异值的滚动轴承故障诊断*

侯一民 ，孙嘉兵 ，张 宇 ，陈艳虎

(1.东北电力大学 自动化工程学院, 吉林 吉林 132012；2.大唐珲春热电厂, 吉林 珲春 133300)

基于PSO-BP神经网络和Hilbert谱奇异值的滚动轴承故障诊断*

侯一民1，孙嘉兵1，张 宇2，陈艳虎1

(1.东北电力大学 自动化工程学院, 吉林 吉林 132012；2.大唐珲春热电厂, 吉林 珲春 133300)

Hilbert谱奇异值是对振动信号进行Hilbert-Huang变换得到Hilbert谱时频矩阵后，再利用奇异值分解的方法提取矩阵的特征得到的。将振动信号的谱奇异值作为故障特征，用粒子群优化BP神经网的方法来诊断故障类型，并将该方法与传统BP神经网络做比较分析，实验结果证明，该方法具有收敛速度快、准确度高的特点。

滚动轴承；希尔伯特谱；奇异值分解；粒子群算法；BP神经网络

0 引言

滚动轴承作为大型旋转机械的关键部件之一，其故障将直接导致设备运行失稳和严重的后果。滚动轴承是旋转轴承中的易损部件，当滚动轴承存在故障时，它们的振动信号表现出非线性、非平稳特征。滚动轴承振动信号包含了大量的轴承运行状态信息，是对轴承故障分析的主要手段之一。主要方法有时频分析方法，即同时提取振动信号时域和频域的局部信息，在故障诊断领域得到了广泛的应用，如小波变换[1-2]方法由于具有多分辨率的特性，广泛应用于故障诊断领域，但小波基函数选择问题是小波分析的一个难题。Huang等人提出了一种自适应的时频分析方法，主要方法是利用经验模态分解(EMD)得到本征模函数(IMF)，该方法在故障诊断领域已经取得较好的效果。张超等[3]利用齿轮箱振动信号经过EMD分解后得到本征模函数(IMF)，然后将IMF的能量熵作为故障特征，对齿轮的裂纹和断齿进行故障诊断。程军圣等[4]提出了一种基于本征模函数的奇异值分解和支持向量机的故障诊断方法，该方法利用本征模函数形成向量矩阵，然后对该矩阵进行奇异值分解，将其作为故障特征向量。相比较而言，利用希尔伯特谱进行故障特征提取的文献很少，于德介等[5]提出一种基于时频熵的故障诊断方法，该方法将希尔伯特谱时频平面等分为面积相等的时频块，然后对其中的每块进行能量归一化处理，结果表明，不同工况下的时频熵不同。因此故障状态下的希尔伯特谱中包含了丰富的故障信息，因此，通过希尔伯特谱进行特征提取来进行故障诊断具有重要的研究价值。

本文将奇异值分解用于故障特征特征提取，用EMD方法将轴承振动信号分解为IMF分量之和，然后对每个IMF分量进行希尔伯特变换得到时频矩阵，接着对时频矩阵[6]进行奇异值分解，得到的奇异值表征了振动信号希尔伯特谱的时频结构特征，将奇异值作为轴承故障诊断的特征向量，针对传统的BP神经网络存在易陷入局部极小值的缺点，本文将采取粒子群优化BP神经网的方法来诊断故障类型，并将该方法与传统BP神经做比较分析，实验结果证明，该方法具有收敛速度快、准确度高的特点。

1 Hilbert谱奇异值

1.1 Hilbert谱

Hilbert-Huang变换由EMD方法和相应的Hilbert谱时频矩阵，它首先将信号进行经验模态分解(EMD)，然后再对获得的所有IMF分量进行Hilbert变换得到Hilbert谱时频矩阵，即该信号的Hilbert谱。Hilbert谱包含了信号丰富的时频信息，是可以表征为信号的时频分布三维谱图。

由文献[7]可知，原始信号经过EMD分解后可表示为：

(1)

(2)

式中P是柯西主分量。

(3)

式中

(4)

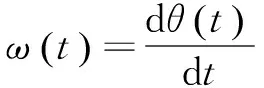
在这里，瞬时频率应该有意义，因此，时间序列在做希尔伯特变换后，要求是单组分的，而性能良好的IMF满足这一条件。每个本征模函数序列可表示为下式：

(5)

1.2 奇异值分解

奇异值分解是矩阵理论中一种重要的矩阵分解，奇异值分解的稳定性能好，即矩阵中的某些元素发生小幅度的变化时，其奇异值变化也较小。此外，旋转不变形与比例不变形是奇异值分解所具备的特性[8]。

矩阵A∈Rm×n，则存在正交矩阵

(6)

(7)

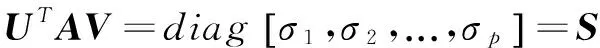
A=USVT

(8)

则式(8)为矩阵A的奇异值分解。U和V分别是A的奇异向量。

由于将故障振动信号进行希尔伯特黄变换后得到的谱时频矩阵后，矩阵维数较高，包含的数据量大，不利于下一步的分析，本文对得到的振动信号Hilbert谱进行奇异值分解。选取轴承各种工况下的振动信号得到Hilbert谱经过奇异值分解后的前50个奇异值作为特征值[9]，其中轴承的运行工况分别为的正常状态、内圈故障、滚动体故障、外圈故障。从图1中可以看到，轴承的振动信号在不同工作状态下的Hilbert谱奇异值不相同，其中故障时的奇异值比正常情况下的奇异值比偏大，轴承在外圈故障时的奇异值明显增大，而且，在不同轴承故障状态下的Hilbert谱奇异值也不相同。由于故障状态下的希尔伯特谱中包含了丰富的故障信息，并且奇异值分解具有良好的稳定性，将该方法用于特征提取，具有稳定性能好，故障分类效果明显的特点。

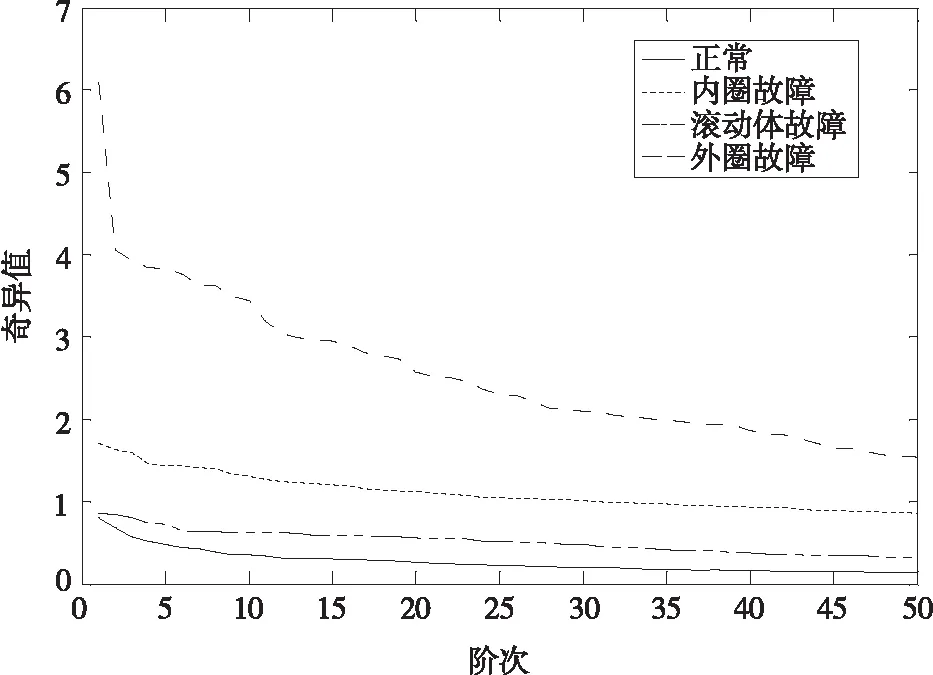
图1 四种工况轴承信号Hilbert谱奇异均值

2 PSO算法原理

粒子群算法(PSO)是一种基于自然界鸟类和鱼类的简单社会模型的智能算法。PSO算法进行优化时，每一个个体被称为一个“微粒”，决定其飞行方向与距离的速度取决于优化函数的适应度值。PSO算法随机初始化为一群粒子搜索最优解，在单次迭代过程中，粒子通过动态跟踪个体极值和全局极值来更新自己的速度和位置，其中pbest为个体极值，pbest是粒子本身目前所找到的最优解；gbest为全局极值，gbest为整个种群目前找到的最优解[10]。两个最优值找到后，粒子根据以下公式更新自己的速度和位置：

(9)

x=x+v

(10)

式中：c1、c2为学习因子；v、x为每个粒子的速度和位置；ω为加权系数。

PSO算法在解空间内寻优时，有时粒子会陷入局部最优解，为了避免这种现象，平衡全局和局部寻优能力，ω可随着迭代次数的增加，最大加权因子ωmax线性减小到最小加权因子ωmin，公式表示为：

(11)

式中：iter为当前迭代次数；itermax为最大迭代次数。

3 基于PSO优化BP神经网络算法

将BP神经网络算法与粒子群优化算法结合，其本质就是将BP神经网络的权值和阈值映射为粒子群中的粒子，并通过粒子的速度与位置不断更新来优化这些参数，从而实现网络的训练[11]。本文选择各种工况下的Hilbert谱前4个奇异值作为特征向量作为输入向量训练神经网络，其中BP网络采用层数结构为4-5-4。

在训练网络时，需要建立一个合理的粒子模型并确定适应度函数。适应度函数使用网络的实际输出与期望输出值之间的均方误差平方和来表示：

(12)

式中：N为训练样本总数；C为输出节点数；yij为网络的实际输出；tij为网络的期望输出。

4 应用

故障诊断所用的振动数据来自于美国凯斯西储大学轴承数据[12]中心，故障类型有外圈故障、滚动体故障和内圈故障，采样频率为12kHZ，本文选择各种工况下的Hilbert谱前4个奇异值作为特征向量，故障模式采用二进制表示，其对应关系见表1。

表1 故障原因与模式对应关系

为了缩短网络训练时间，对本文的24组数据进行预处理，采用最大最小归一法，把数据统一到[-1,1]区间：

(13)

本文将样本数据的前20组作为训练样本，其余4组作为测试样本，采用的BP神经网络结构为4-5-4。定义粒子群规模为20，最大迭代次数为50，其中粒子群学习算法中学习因子c1=c2=1.49445，惯性权重ωmax=0.9,ωmin=0.4，预设误差为10-8。

本文通过matlab软件，对比分析PSO-BP算法与BP算法的网络训练均方误差，图2中BP神经网络在训练初期速度下降很快，但在下降到20步时曲线趋于平缓，在训练达到100步时，训练完成，但无法达到预设10-8的误差要求；图3中PSO-BP神经网络在训练步数为4步时，收敛完成。并且了达到10-8的误差要求。对比图2和图3可知，采用PSO-BP神经网络进行故障诊断可以使网络迅速收敛且训练步数大大减少。识别结果见表2。

表2 诊断结果

图2 BP神经网络训练误差曲线

图3 PSO-BP神经网络训练误差曲线

5 结论

本文利用振动信号的Hilbert谱的奇异值作为轴承故障诊断的特征，该方法是一种故障信号特征提取的新方法,并通过实验验证，可以准确的提取轴承故障特征。利用粒子群优化BP神经网的方法来训练神经网络，该方法与传统BP神经做比较分析，在收敛速度、准确度上均有显著提高，满足了大型旋转机械故障诊断的要求，具有一定的工程应用价值，为大型旋转机械的故障诊断提供了一种有效的途径。

[1] 程发斌，汤宝平，赵玲.最优Morlet小波滤波及其在机械故障特征分析中的应用[J]中国机械工程，2008,19(12):1437-1441.

[2] 崔铃丽，高立新，殷海晨，等.基于第二代小波的复合故障诊断方法研究[J].中国机械工程,2009,20(4):442-446.

[3] 张超，陈建军，郭迅.基于EMD能量熵和支持向量机的齿轮故障诊断方法[J].振动与冲击，2010,29(10):216-220.

[4] 程军圣，于德介，杨宇.基于内禀模态奇异值分解和支持向量机的故障诊断方法[J].自动化学报，2006,32(3):475-480.

[5] Yu Dejie,Yang Yu,Cheng,Junsheng.Application of Time-frequency Entropy Method Based on Hilbert-Huang Transform to Gear Fault Diagnosis[J].Measurement,2007,40(9/10):823-830.

[6] 赵志宏，杨绍普，李韶华.基于Hilbert谱奇异值的轴承故障诊断[J].中国机械工程，2013,24(3):346-350.

[7] 胡劲松，杨世锡，任达千.一种基于EMD的振动信号时频分析新方法研究[J] .振动与冲击，2008,27(8):72-73.

[8] Cempel C.Generalized Singular Value Decomposition in Multidimensional Condition Monitoring of Machines-A Proposal of ComparativeDiagnostics[J].Mechanical Systems and Signal Processing,2009,23(3):701-711.

[9] 赵志宏.基于振动信号的机械故障特征提取与诊断研究[D].北京：北京交通大学，2013.

[10] 郝静，朱峰，兰华,等.基于模糊PSO-BP神经网络的配电网故障选线方法[J] .电测与仪表，2011,48(552):53-56.

[11]李九宝.基于人工智能优化算法的聚丙烯熔融指数预报建模优化研究[D].杭州：浙江大学，2012.

[12]The Case Western Reserve University Bearing Data Center Website .Bearing Data Center SeededFault Test Data[EB/OL].[2011-11-12].http //cse-groups.case.edu/bearingdatacenter/home.

(编辑 李秀敏)

Fault Diagnosis of a Rolling Bearing Based on PSO-BP Neural Network and Hilbert Spectrum and Singular Value Decomposition

HOU Yi-min1,SUN Jia-bing1, ZHANG Yu2,CHEN Yan-hu1

(1.Dept.of Automation Engineering,Northeast Dianli Univ.,Jilin Jilin 132012,China;2. Datang Hunchun Thermoelectric Plant , Hunchun Jilin 133300,China)

Hilbert spectrum and Singular value Decomposition is Hilbert-Huang transform of Vibration signal Hilbert spectrum matrix,and using the singular eigen value value decomposition method to extract matrix. then,get the vibration signal spectrum singular value as the fault feature,The method of particle swarm optimization BP neural network to diagnose the fault type.The experimental results show that, this method could identify the effective application in rolling bearing fault.

rolling bearing; Hilbert spectrum;singular value decomposition;particle swarm optimization;BP neural network

1001-2265(2014)07-0077-03

10.13462/j.cnki.mmtamt.2014.07.021

2013-9-25;

2013-10-27

国家自然科学基金项目(41076060)；吉林省教育厅“十二五”科研规划项目([2011]80)；吉林市科技计划项目(201162505)

侯一民(1978—)，男，吉林省吉林人，东北电力大学副教授，工学博士,主要研究方向为模式识别与智能系统、检测技术与自动化装置 ,(E-mail)ymh7821@163.com;通信作者：孙嘉兵(1988—),男，吉林省吉林人，东北电力大学硕士研究生，主要研究方向为旋转机械故障诊断、检测技术与自动化装置，(Email)715065703@qq.com。

文献标识码：A