基于最大工作空间的DELTA机器人尺寸综合与优化*
2014-07-18南文虎唐小琦
南文虎,宋 宝,唐小琦
(华中科技大学 国家数控工程中心,武汉 430074)
基于最大工作空间的DELTA机器人尺寸综合与优化*
南文虎,宋 宝,唐小琦
(华中科技大学 国家数控工程中心,武汉 430074)
在DELTA机器人的工程设计中,需要选取适当的机构参数,其中机构杆长是一个很重要的参数。解决机构的尺度综合问题是非常必要的。文章利用DELTA机器人的物理模型,运用代数法和几何法,在机构设计空间内,对特征杆长进行无量纲分析,找到关键机构尺寸,进行归一化处理;对其工作空间进行拓扑分类和体积计算,找到最佳杆长向量(依据工作空间体积最大);在工程应用中,为此类机器人的设计和制造提供一定的理论指导。
DELTA机器人;尺寸综合;无量纲 ;杆长向量
0 引言
DELTA机构最早是由瑞士的Reymond clavel教授与1985年提出的,由于它只有三个平移自由度,设计、制造、控制都比较简便,在工业生产有广泛的应用[1-3]。但是,它的工作空间相对串联机器人来说,相对要小很多,所以在设计此类机器人时,如何规划出最优的机构普适参数,在机构特征尺寸确定的情况下,使得机器人的相对工作空间最大,是一件很必要的工作。针对机构空间物理参数,用无量纲的方法对DELTA机器人的工作空间进行全域分析,找到杆长向量与工作空间体积的映射图[4],但没有求出杆长向量的极值。利用计算机辅助设计,在给定的工作空间,规划出最优的机构尺寸[5-6],但是这种方法只适合特定的设计,不适合系统化的设计。
本文在理论上,采用无量纲的分析方法,运用几何法和代数法,分析了机器人的奇异性,尺寸综合是在保证并联机构实现预定工作空间的前提下,以操作性能最优为目标确定机构的尺度参数,进行无量纲的尺寸归纳分析,不仅对此类机构有总体的空间认识,而且容易在杆长向量空间中,找到最佳杆长向量的分布规律,这样对于机构尺度综合和此类机器人结构设计,具有更加普遍性的意义。
1 DELTA机器人的物理尺寸分析
如图1所示,为DELTA机器人的机构示意图,总体结构上由静平台、动平台、三组平行四边形机构、三个转臂构成,三组平行四边形机构消除了动平台的转动自由度,只剩下三个平移自由度,机械结构整体上、紧凑、简洁、驱动部分布置在静平台上,这些特点,使它具有良好的运动学和动力学特性,因此,在工业机器人中,DELTA机器人占有重要的一席之地。
L+R+r=100
(1)

图1 DELTA机器人结构示意图
2 机构的位置反解分析
如图1、图2所示,建立定坐标系o-xyz、o-xiyizi、Bi-xiyizi,动坐标系o-x′y′z′,作为计算的仿射坐标系,在定坐标系o-xyz中,根据矢量运算法则,得:
OO′=OBi+BiEi+EiPi+PiO′
(2)
EiPi=oo′-(oBi+BiEi+Pio′)
(3)
(4)
将坐标值代入上式,得:

图2 DELTA机器人归一化杆长分布与坐标架示意图
[(L1-L2+Rsinθi)cosηi-x]2+ [(L1-L2+Rsinθi)sinηi-y]2+[Rcosθi-z]2=r2
(5)
将特征尺寸L=L1-L2,代入上式,即有:
[(L+Rsinθi)cosηi-x]2+
[(L+Rsinθi)sinηi-y]2+[Rcosθi-z]2=r2
(6)
当i=1~3,(x、y、z)已知时,由上式(6)可列出一个三元三次方程方程组,从而可以求出机器人的位姿反解(θ1、θ2、θ3)。
3 工作空间解析
3.1 (100>R≥r>0时)工作空间解析
在设计空间内,分析工作空间的解析形式,在定坐标系o-xyz中,对每一条支链,式(6)表示球心位于(((L+Rsinθi)cosηi,(L+Rsinθi)sinηi,Rcosθi),半径为R的球面。当θi从0°变化到360°时,工作空间则是由此球面所形成的包络体,如图3所示,其外边界为以yi轴为轴线的圆环面,在Bi-xiyizi坐标系中,此实体圆环的边界曲面方程为:
(7)
将上式利用下面坐标变换公式:
(8)
转化在o-xyz坐标系中,当i=1、2、3时,由式(8)可以组合成三元三次方程组,当r∈(0,const)时,离散r值,解此方程组,则其解集构成全域工作空间。
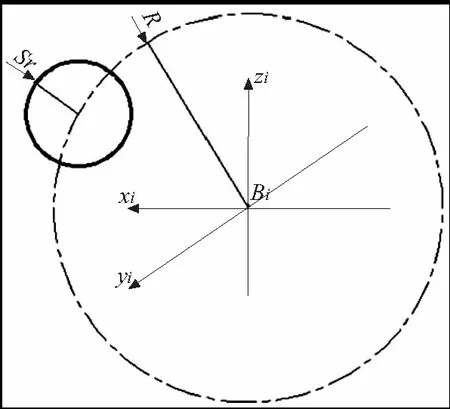
图3 单开链子空间边界圆环面成形截面示意图
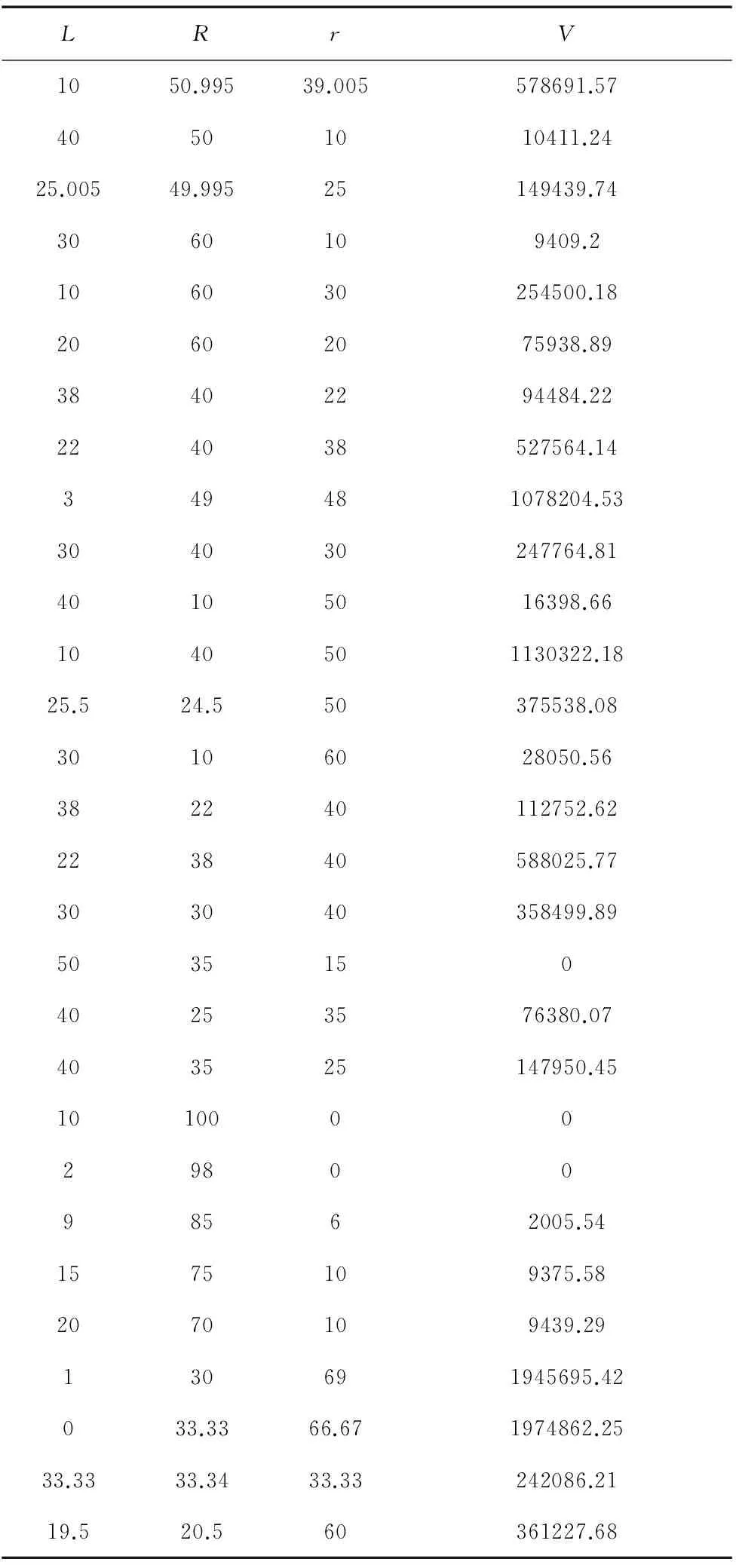
3.2 (0 当0 图4 单开链子空间边界镂空鼓形成形截面示意图 (9) 其内边界曲面方程如下式(10)所示, (10) 将以上两个方程转化在o-xyz坐标系中,当i=1、2、3时,可以组合成三元三次方程组,当r∈(0,const)时,离散r值,解此方程组,其解集构成全域工作空间。 3.3 工作空间为非空集时的杆长分析 杆长在设计空间中,满足一定的条件下,上式方程组才有解,根据以上解析分析,可知当: r+R≥L (11) 时,上述三元三次方程组的解空间有解,且当: r+R=L (12) 方程只有一解,此时机构退化为构件状态。 所以机构有解集存在的条件是 : r+R>L (13) 将以上(12)式代入(13)式,化简,得: L<50 (14) 由式(11)、(12)与(14),结合杆长必须满足的几何条件,得: 0≤L<50、0 (15) 在无量纲的归一化的设计空间里,图5展示了的杆长向量分布图,图中梯形ABCD为设计空间区域,其中包含边界CD线,对应L=0。 图5 DELTA机器人归一化杆长分布示意图 3.4 单开链子工作空间体积解析 当杆长向量位于设计空间的BEFC时,r≤R,如图3所示,此时形成一实心圆环包络体,此实心圆环体的体积: V=2πR(πr2)=2π2*(100-r)*r2 (16) 当杆长向量位于设计空间的AEFD时,r>R,如图4所示,此时形成镂空鼓形包络体,此包络体的体积: V= (17) 即, V=2π2*(100-r)*r2 (18) 画出r-V函数关系图,如图6所示: 图6 单开链子空间r-V函数关系图 从图6可以看出:①当V取最大值时,对应的r≈66.7,V=2.924×106,此时R=33.33, 单支链杆长比例:R/r=2;②在r≈66.7的两侧,单支链工作空间体积值呈减小趋势,但在r≈66.7的右侧(r>66.7),随着r值的增大,工作空间体积减小的更快。 如上图5所示,在设计空间中,平面ABCD为机器人杆长向量的分布空间,根据杆长比例与所对应工作空间拓扑形状的相似性,采用定性分析的方法,归纳为如图7所示的21种不同类形的工作空间,进一步总结分析,可以发现有以下特点: 最后,要保证政策法规的有效落实。改革不仅要落实到政策上,更要落实到行动上,不能光是“喊喊口号,开开大会”,而是要针对地方实际和以往改革的具体实践,把上级的政策指示摸清吃透,坚决杜绝以文件落实文件、以口号回应口号的状况出现。必须始终保持对党的事业忠诚、对党赋予的任务踏实干好的心态,把改革事业扎扎实实地悟透、干好。 (1)当R为最大值时,区域BGK,EG、KB线上,形成实心曲面实体,结构上有很大的相似性; (2)区域BEG、BFC形成实心曲面实体,结构上相似; (3)区域AFG、DPF、GKF形成有镂空的曲面实体,结构上相似; (4)区域AEG(包含G点)形成实心三叶形曲面实体; (5)P点和K点分别形成凹起尖点和凸起尖点,形成反对称性; (6)区域ADP内,工作空间位置相对呈现分离态,距设计基准有一定距离。 图7 工作空间相似形状分类图 利用本文第3部分中的解析表达式,可以求出工作空间体积,但是相对计算量大,本文利用三维软件SOLIDWORKS画出在特定杆长向量时,所对应的工作空间,然后利用软件自带的测量工具,测出它的几何体积,如表1所示,最后利用插值的方法,画出杆长向量与工作空间的映射关系图,进一步进行尺寸综合。 表1 杆长向量与工作空间体积的数据表(单位为1) 采集上表1中的数据,用matlab中的griddata差值函数进行差值绘图,绘制如图8所示的机器人工作空间体积V与特征杆长向量(L,R,r)之间的函数关系图,利用此图,对机器人杆长进行尺寸综合,得出以下结论: (1)工作空间体积V与特征杆长L成反比,L越大,V越小; (2)当L一定时,工作空间体积V,在R=33.33处,V呈现最大值,在R=33.33的两侧,V值减小; (3)特征杆长向量的值为(0,33,33,66.67)时,工作空间体积V取最大值。 图8 归一化工作空间体积与设计空间杆长向量之间 的函数关系图 本文的创新点在于:①系统性的从无量纲归一化的设计空间与相应机构工作空间的联系性出发,定量的分析了机器人的工作空间体积;②从机器人的工作空间体积入手,进行机构尺寸综合,找到工作空间体积与设计空间杆长向量之间的函数关系图,找到工作空间体积最大时,所对应的杆长向量最优值。以上工作,为此类机器人的杆长选取提供一定的理论指导。 根据以上研究,研制出了一款DELTA机器人,投入某企业生产线中,取得了不错的经济效益。本文的研究不仅为后续动态优化提供基础[7-9],而且对于DELTA机器人的实际工程应用,有广泛的指导意义。 [1] 高秀兰,鲁开讲,王娟平. Delta并联机构工作空间解析及尺度综合[J].农业机械学报,2008,39(5):146-149. [2] 张立杰,刘辛军.一种并联机构最大内切空间的几何求解[J].机械设计与研究,2002,18(1):20-22. [3] 颜兵兵,刘秀民,解明强,等. 3-UPS并联机器人工作空间研究[J].组合机床与自动化加工技术, 2012(6):38-41. [4] X-J Liu,J Wang,H Zheng. Workspace atlases for the computer aided design of the Delta robot[J].Journal of Mechanical Engineering Science,2003,2(17):861-869. [5] R. Neugebauer1 , W.G. Drossel1 , C. Harzbecker1 , et al. Method for the Optimization of Kinematic and Dynamic Properties of Parallel Kinematic Machines.Annals of the CIRP . 2006 ,55(1). [6] M.A. Laribi, L. Romdhane, S. Zeghloul.Analysis and dimensional synthesis of the DELTA robot for a prescribed workspace[J]. Mechanism and Machine Theory, 2007, 42(7):859-870. [7] Ridha Kelaiaia, Olivier Company, Abdelouahab Zaatri.Multiobjective optimization of a linear Delta parallel robot. Mechanism and Machine Theory[J], 2012, 50:159-178. [8] Yong jie Zhao.Dimensional synthesis of a three translational degrees of freedom parallel robot while considering kinematic anisotropic property[J].Robotics and Computer-Integrated Manufacturing, 2013, 29(1): 169-179. [9] 张彦斌,党玉功.一类3自由度空间并联机器人机构的设计及分析[J].组合机床与自动化加工技术,2011(2):17-20. (编辑 李秀敏) Optimization and Dimension Synthesis of the DELTA Robot Based on the Maximum Size of Working Space NAN Wen-hu,SONG Bao,TANG Xiao-qi (The National NC System Engineering Technology Research Centre,Huazhong University of Science and Technology,Wuhan 430074,China) The rod length is a very important parameter in the DELTA robot engineering design, so how to select the proper parameters of the mechanism is a necessary thing. Solving the problem of scale synthesis of mechanism is very significant. Based on the physical model of DELTA robot, using the algebraic method and geometric method, Eigen rod length is analyzed by Non-dimensional method and is normalized with according to the key rod length size in the design of spatial mechanism; Topological classification and calculation of the volume of the work space are proposed to find the best length vector (according to the maximum workspace volume ); It provides some theoretical guidance for the design and manufacture of this kind of robot in engineering application. DELTA robot;scale synthesis;non-dimensional method;length vector 1001-2265(2014)07-0038-04 10.13462/j.cnki.mmtamt.2014.07.011 2013-11-28; 2013-11-02 高等学校博士学科点专项科研基金(新教师基金课题)(20090142120035) 南文虎(1985—), 男, 华中科技大学博士研究生,主要从事工业机器人的结构设计与控制,(E-mail)nanwenhu@163.com。 TH112;TG65 A



4 工作空间拓扑结构分类

5 CAD工作空间体积数值计算与尺寸综合

6 结论
