简支梁动力系数与列车速度的关系研究

张 军 耿丽君

(1.中铁第四勘察设计院集团有限公司，湖北武汉 430063;2.武汉大学珞珈学院，湖北武汉 430063)

1 概述

桥梁动力系数是桥梁动力放大效应的指标，是车桥系统的动力特性和相互作用的综合反映。我国常用的低中速铁路桥梁规范以及设计、检定中并不区分位移、内力动力系数［1］。欧洲UIC活载动力系数［2］针对不同的线路考虑了弯矩和剪力动力系数，我国高速铁路设计规范规定的ZK活载动力系数［3］将弯矩和剪力动力系数区分开来，给出了不同的表达式。日本新干线动力系数的取值与桥梁跨度、桥梁自振频率、速度等参数有关，没有区分位移和内力动力系数。

本文根据弹性系统动力学总势能不变值原理及形成系统矩阵的“对号入座”法则［4］，建立了列车—有砟轨道—桥梁系统竖向振动的矩阵方程，编制了相应的计算机程序，分别计算了高速列车通过简支梁桥时，不同位置、不同类型的动力系数，探讨了不同类型、不同位置动力系数随速度的变化规律。

2 建立模型

动车组模型选用一个4轴车辆，由1个车体、2个转向架、4个轮对组成，车体由一系悬挂、二系悬挂连接而成，见图1。车体、转向架、轮对模拟为刚体，只考虑车体和转向架点头和沉浮的自由度。假定轮对与钢轨密贴，故单个车辆只有6个独立自由度。从车辆最右侧轮对一上桥就开始计算，到车辆最左侧轮对离开桥梁时终止计算。

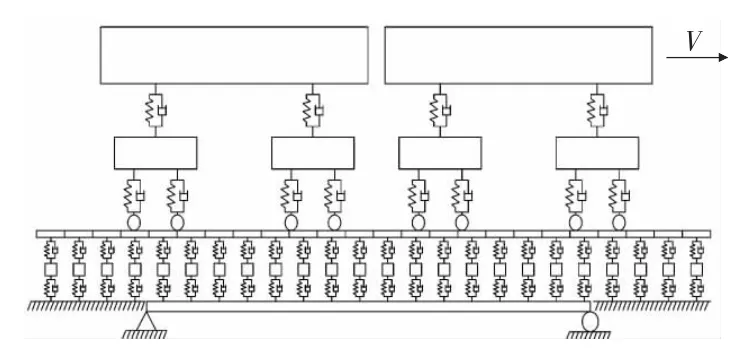
图1 列车—有砟轨道—桥梁系统竖向振动有限元模型

桥梁结构采用平面梁单元，以高速铁路32 m双线整孔预应力混凝土简支箱梁为研究对象［2］，钢轨也采用平面梁单元。轨枕视为刚体，轨枕与钢轨之间以及轨枕与桥梁之间单元用线性弹簧和粘性阻尼元件来模拟，建立了列车—有砟轨道—桥梁系统模型(见图1)。

计算考虑了离散轨枕和扣件弹簧的列车与桥上有砟轨道相互作用系统的总势能，然后利用弹性系统动力学总势能不变值原理及形成系统矩阵的“对号入座”法则，得到如下的振动方程，其分块矩阵形式如下:

采用Wilson-θ法求解该振动方程并利用FORTRAN 90语言编制系统竖向振动的计算程序。

3 计算选用参数

采用CRH3动力分散式列车组的车辆参数，无砟钢轨参数采用文献［5］［6］中的参数，桥梁参数采用表1。

表1 高速铁路简支梁参数［1，7］

4 验证竖向振动系统模型

为了验证程序的可靠性，在列车—有砟轨道—桥梁系统模型中去除轨道，采用与文献［8］相同的计算参数演算4轴车辆在简支Euler梁上的动态响应，见图2～图5，原文通过有限元法和模态分析法得到相同的结果，对比可见，本文计算的车桥响应与原文完全一致，因此本文推导的车辆—轨道—桥梁系统振动模型和编制的程序是正确的。

图2 车体质心竖向位移时程曲线

5 不同位置和类型的桥梁动力系数

为了比较位移动力系数、弯矩动力系数和剪力动力系数在桥梁同一位置的变化情况，计算了CRH3动车组以不同速度通过32 m简支梁桥的数据，如图6，图7所示。

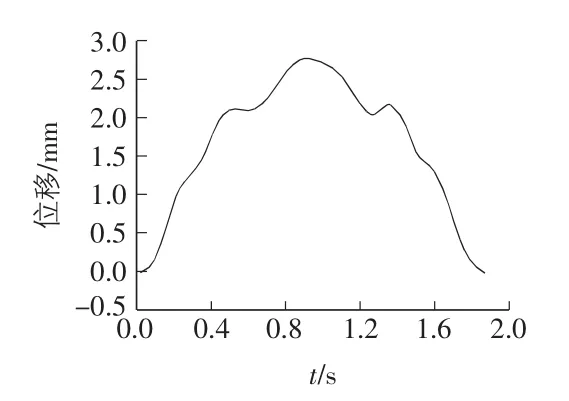
图3 梁中点竖向位移时程曲线

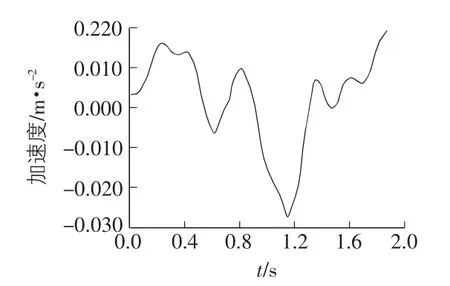
图4 车体质心竖向加速度时程曲线

图5 梁中点竖向加速度时程曲线

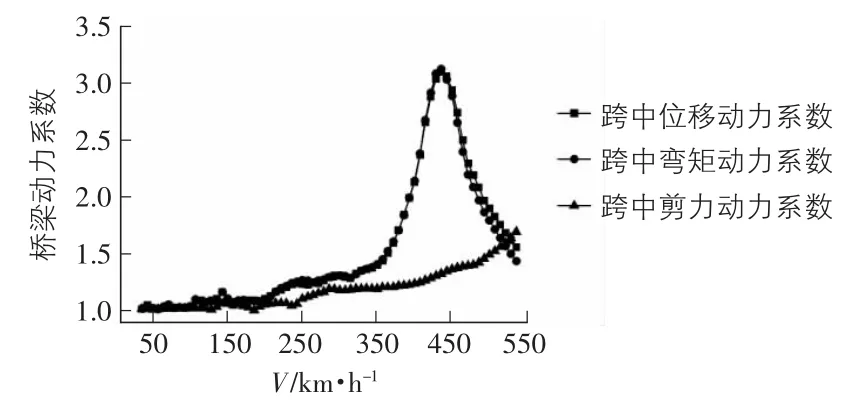
图6 梁跨中的三种动力系数随速度变化图

图7 梁3/4处的三种动力系数随速度变化图

在0 km/h～430 km/h速度范围内，跨中位移动力系数和弯矩动力系数在变化趋势和数值大小上基本一致，在430 km/h出现明显的动力系数峰值且数值相同。在430 km/h～550 km/h速度范围内跨中位移动力系数和弯矩动力系数都呈减小的趋势，前者在数值上略大于后者。在0 km/h～200 km/h速度范围内，跨中剪力动力系数变化趋势与前两者基本一致，速度大于200 km/h时，剪力动力系数变化随速度增大而增大，无峰值变化。在0 km/h～400 km/h速度范围内，3/4跨处的位移动力系数、弯矩动力系数和剪力动力系数在变化趋势上基本一致，数值上三者也相差不大。在400 km/h～550 km/h速度范围内剪力动力系数的变化趋势和数值与另两者不同。

在实际运营速度0 km/h～350 km/h范围内，3/4跨处的三种类型的动力系数变化趋势基本一致，该位置处的动力系数较跨中更能反映桥梁位移、内力随着速度增大的动力特性。

为了研究32 m简支梁桥1/4跨处、跨中处、3/4跨处的动力系数与速度的关系，对CRH3动车组过桥进行了计算，结果如图8～图10所示，分别列出了位移动力系数在桥梁1/4跨处、跨中处、3/4跨处速度的变化趋势、弯矩动力系数在桥梁1/4跨处、跨中处、3/4跨处速度的变化趋势、剪力动力系数在桥梁左右支座处、3/4跨处速度的变化趋势。

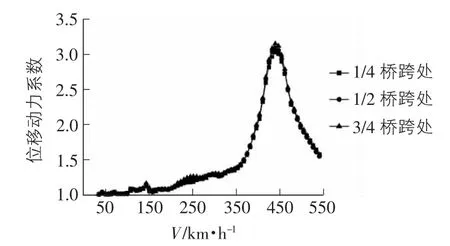
图8 位移动力系数在不同位置随速度变化曲线

位移动力系数在桥跨1/4处、跨中处、3/4处的变化趋势基本一致，这说明桥梁各个部分参与振动的模态是完全一致的［9］。3/4梁跨处的动力系数在数值上略大于其他位置的动力系数，更具有代表性。

图9 弯矩动力系数在不同位置随速度变化曲线

弯矩动力系数在梁跨1/4处、跨中处、3/4处的变化趋势相近，在共振峰值上跨中弯矩动力系数大于3/4处弯矩动力系数，大于1/4处。

剪力动力系数在桥梁左右支座处的变化趋势基本一致，数值也相近。剪力动力系数在支座处较3/4跨处的变化趋势有所不同。

6 结语

本文建立了列车—有砟轨道—桥梁竖向振动模型，利用弹性系统动力学总势能不变值原理及形成系统矩阵的“对号入座”法则推导出了系统竖向振动的矩阵方程，利用Wilson-θ法进行振动方程的求解，并编制了相应的计算机程序，通过算例的验算，证明本程序是有效的。计算了桥梁不同位置的位移、内力动力系数并总结了相关规律，得出在0 km/h～350 km/h速度范围中的简支梁，3/4跨处的三种类型的动力系数变化趋势基本一致，3/4跨处的动力系数较跨中更能反映桥梁位移、内力随着速度同时增大的动力特性。

［1］中华人民共和国铁道部.铁路桥梁检定规范［M］.北京：中国铁道出版社，2004.

［2］孙树礼.高速铁路桥梁设计与实践［M］.北京：中国铁道出版社，2011.

［3］TB 10621-2009，高速铁路设计规范(试行)［S］.

［4］曾庆元.弹性系统动力学总势能不变值原理与列车桥梁时变系统振动分析［J］.铁道建筑技术，2001(1)：10-12.

［5］翟婉明.车辆—轨道耦合动力学［M］.第3版.北京：科学出版社，2007.

［6］娄 平.列车—轨道(桥梁)系统竖向振动分析［D］.长沙：中南大学，2007.

［7］路 萍.高速列车通过桥梁时的变速效应和振动控制研究［D］.长沙：中南大学，2008.

［8］Long P，Zeng Q Y.Formulation of vertical equations of motion of finite element form for vehicle-bridge interaction system［J］.Journal of Structural Engineering，2005.

［9］沈锐利.高速铁路桥梁与车辆耦合振动研究［D］.成都：西南交通大学，1998.