波形钢腹板箱梁桥车桥耦合振动冲击系数研究

陈志兴

(华东交通大学土木建筑学院，江西南昌 330013)

1 概述

波形钢腹板PC组合箱梁桥是用波形钢腹板取代混凝土腹板或平钢腹板的一种新型箱梁结构。自从20世纪80年代末期法国建造了世界上第一座波形钢腹板PC组合箱梁桥——Cognac桥，此后世界上一些国家相继采用了该种箱梁结构。波形钢腹板PC组合箱梁桥相对于传统混凝土腹板箱梁桥有诸多优点:1)波形钢腹板抗剪切刚度大，解决了混凝土腹板开裂问题;2)波形钢腹板轴向伸缩刚度几乎为零，它对混凝土上、下顶底板徐变、收缩变形不起约束作用，大大提高了预应力利用效率;3)用波形钢腹板替代混凝土腹板，减轻了桥梁上部结构重量，从而减小了下部结构尺寸，降低桥梁总造价等等一些优点。

但以往的研究多是针对其静力学展开的，对该种桥型的动力学方面研究还是比较滞后的。本文是以实际工程背景泼和大桥为实例，研究了车速、路面不平顺、桥梁阻尼对冲击系数值的影响;并在最后总结了各国规范得出的冲击系数值，对数值解进行了对比分析。

2 动力分析模型的建立

2.1 工程背景简介

为了分析各种因素对波形钢腹板箱梁桥的影响。本文选择了泼和大桥为桥梁分析模型。泼和大桥是国内第一座波形钢腹板PC组合箱梁公路桥，桥梁模型采用泼和大桥为冲击系数计算模型。全桥为4×30 m连续梁，桥宽为13 m+2×1.5 m，设计采用等高截面，截面高1.6 m，顶、底板厚 0.15 m，腹板厚 0.008 m，波形钢腹板斜交角为20°，设计荷载为公路—Ⅰ级。

2.2 桥梁有限元模型

采用通用有限元软件ANSYS建立桥梁模型。顶、底板及腹板单元选为Shell63单元，腹板与顶、底板连接采用接触单元Contal169，Targe175进行模拟。全桥共划分为97 019个单元，86 958个节点。约束采用在跨中一端支座处约束节点X，Y，Z平动自由度，其他支座处约束X，Y平动自由度。桥梁有限元模型图及波形钢腹板局部图见图1，图2。

图1 桥梁有限元模型图

图2 波形钢腹板局部图

2.3 桥梁动力特性

采用子空间迭代法提取桥梁前十阶振型及相应频率，限于篇幅，只列出前四阶振型图，桥梁前十阶频率如图3，表1所示。

3 车桥耦合振动方程

车桥耦合振动分析采用将桥梁与车辆分为两个子系统，分别建立各自振动方程，通过桥梁与车轮接触点几何相容条件与力的平衡关系来进行耦合。论文计算采用模态综合技术，即广义坐标离散的方法:首先求出桥梁自由振动的频率与振型，利用振型的正交特性，同时桥梁动力响应主要由若干个低阶模态控制，所以大大减少计算工作量，最后方程通过数值分析来进行求解。车辆与桥梁的运动方程分别表示为:

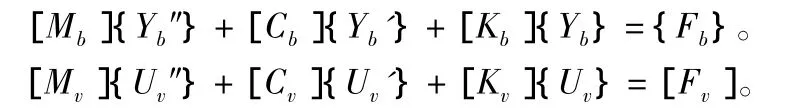
其中，Mb，v为桥梁、车辆的质量矩阵;Cb，v为桥梁、车辆的阻尼矩阵;Kb，v为桥梁、车辆的刚度矩阵;Fb，v为作用于桥梁、车辆的耦合作用力;Yb为桥梁位移;Uv为车辆位移。

车桥耦合系统振动中，车辆振动对桥梁产生的惯性力为:

单个车轮i施加给桥梁的作用力表示为:

其中，Fvi为车轮振动对桥梁产生的惯性力;Zi为i车轮处竖向位移;ri为i车轮处路面不平顺;mig为i车轮分配到的重力;Δi为第i车轮相对于桥面的竖向位移。

图3 桥梁前十阶振型图

表1 桥梁动力特性表

利用Matlab数值计算软件采用Newmark-β逐步积分法求解车桥耦合动力方程。

4 车桥耦合振动响应影响因素分析

冲击系数实质上是考虑移动车辆、桥梁系统相互作用的强迫振动和车辆对桥梁的“冲击”作用等的一个综合性动力系数，定义为如下公式:

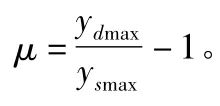
其中，ydmax为梁最大动挠度;ysmax为梁最大静挠度。

本节车辆加载数量为单车，桥梁加载方式为偏载及中载，共分为两个工况，具体加载工况如图4所示。影响车桥耦合振动的因素较多。先后分析了车速、桥面不平顺、桥梁阻尼对冲击系数的影响。

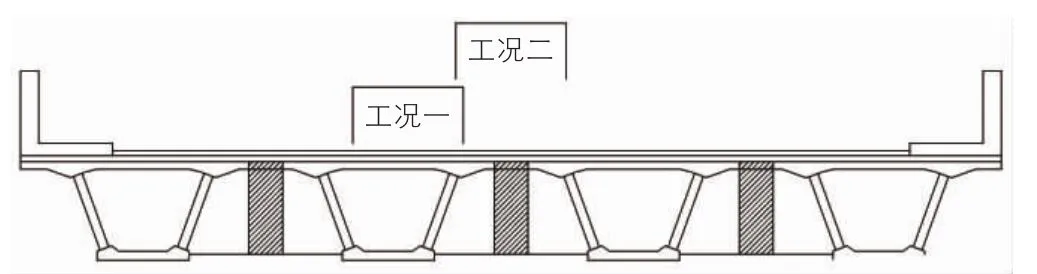
图4 加载工况

4.1 车速对冲击系数值的影响

车辆速度选为从低速到高速，分别为10 m/s，20 m/s，30 m/s，40 m/s，50 m/s。桥梁阻尼比为0.02，暂不考虑桥面不平度的影响，采用matlab编制程序算出各片梁在各工况下的最大动挠度值，限于篇幅，为了分析各因素对冲击系数值的影响，取桥梁各工况下的最大动挠度值进行分析，桥梁最大动挠度为边梁第一跨跨中在偏载下动挠度值。具体动挠度见图5。

具体冲击系数值计算见表2。

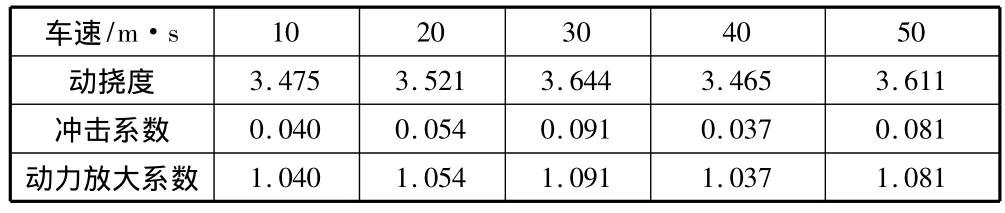
表2 具体冲击系数值

动力放大系数随车速增大变化规律见图6。

从上述边梁各跨中动挠度图中可以看出，车辆行驶速度对边梁各跨中动挠度值影响较明显，随着车速的增加，边梁各跨中动挠度值除个别车速外，呈上升趋势。这一特点在动力放大系数图中也明显体现出来。并且车速越低，动挠度曲线波动越明显，相反，随着车速的增加，曲线的波动越加的平缓。这是因为车速越低，车辆在桥梁上的行驶时间越长，导致车桥耦合振动时桥梁的高频波动得以充分发展。当车速较快时，桥梁的高频波动还没有来得及出现，汽车就已经离开了桥梁，从而动挠度曲线更加的光滑。

图5 边梁在偏载情况下第一跨跨中动挠度图

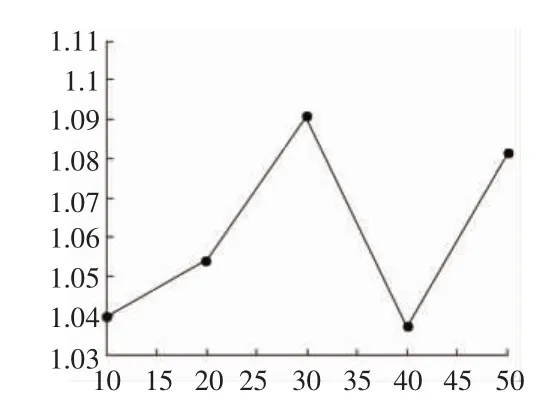
图6 动力放大系数随车速增大变化规律

4.2 路面不平度对冲击系数值的影响

路面不平度具有很大的随机性，目前研究路面平整度时，一般均将其看作平稳的高斯过程，采用路面功率谱对其进行描述。数值模拟路面不平度时主要有三角级数叠加法、快速傅里叶逆变换法、白噪声法等。因而，即使采用同一路面等级，不同方法得出的路面不平度也依然存在很大的随机性。车辆速度为30 m/s，曲线选为边梁在偏载时的第一跨跨中动挠度曲线进行分析，路面不平度分别为光滑路面，A，B，C级路面，桥梁阻尼比为0.02。

从图7可以看出，在相同车速下，随着路面状况的下降，各级路面动挠度曲线围绕着光滑路面动挠度曲线波动幅度越大。所以随着路面状况的下降，桥梁冲击系数值变大。可以得出路面不平度是影响冲击系数的主要因素之一。各级路面冲击系数值见表3。

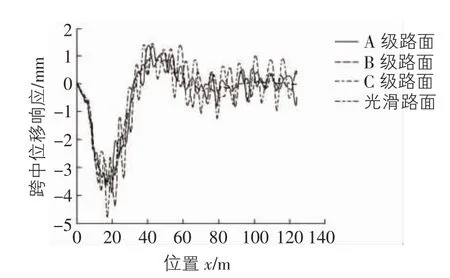
图7 不同路面等级下的桥梁第一跨跨中动挠度

表3 各级路面冲击系数值

4.3 桥梁结构阻尼对冲击系数的影响

桥梁结构阻尼比选用为 0.02，0.05，0.08，车辆行驶速度为20 m/s，不考虑路面不平度对动挠度的影响，边梁在偏载下的各不同桥梁结构阻尼情况下的第一跨跨中动挠度如图8所示。

图8 不同桥梁阻尼对应的边梁第一跨跨中动挠度曲线

阻尼比对冲击系数的影响见表4。

表4 阻尼比对冲击系数的影响

从上述不同阻尼比所对应的桥梁动挠度图及冲击系数表中可以看出，桥梁阻尼能在一定程度上影响桥梁的冲击系数值。图9局部放大图(一)反映出随着阻尼比的增大，能有效的减小冲击系数值;并且从图10局部放大图(二)中可以看出，曲线的波动幅度随着桥梁阻尼比的增大变得更加的平缓。

5 结语

通过本文研究，可以得出以下结论:

1)随着车速的提高，波形钢腹板连续梁桥动挠度及冲击系数值有增大趋势。

2)路面等级是影响车桥耦合振动的主要因素之一，随着路面等级的降低，桥梁冲击系数值显著提高。

图9 局部放大图（一）

图10 局部放大图（二）

3)桥梁结构阻尼能在一定程度上减小桥梁动挠度值。随着桥梁阻尼比的增加，桥梁跨中动挠度值减小，并且，曲线的波动幅度变得更加的平缓。

4)尽管现行规范对冲击系数值的定义较老规范有明显提高，以桥梁基频函数取代以跨径为函数的冲击系数值，但本文得出冲击系数不仅和桥梁基频有关，还与车速、路面不平顺等有关。这在设计中应当引起注意。

［1］Ling Huang，Hiroshi Hikosaka，Keizo Komine.Simulation of accordion effect in corrugated steel web with concrete flanges［J］.Computers and Structures，2004(10)：2061-2069.

［2］尹 航 ，刘保东，任红伟.波形钢腹板箱梁的动力特性分析［J］.公路交通科技，2008(4)：9-10.

［3］韦忠瑄，孙 鹰，沈 庆，等.波形钢腹板PC组合箱梁的动力特性研究［J］.公路交通科技，2011(10)：75-76.

［4］李宏江，万 水，叶见曙.波形钢腹板PC组合箱梁的结构特点［J］.公路交通科技，2006，19(3)：53-57.

［5］宋建永，纪 伦，张树仁.波纹钢腹板钢梁的结构特点和受力性能［J］.广西交通科技，2003，28(105)：15-17.

［6］徐 强，万 水.波纹钢腹板PC组合箱梁桥设计与应用［M］.北京：人民交通出版社，2009.

［7］刘玉擎.组合结构桥梁［M］.北京：人民交通出版社，2005.

［8］DB 41/T 643-2010，公路波形钢腹板预应力混凝土箱梁桥设计规范［S］.