缝纫用线量年度预算方法的探讨

房 利，何永厚

（鲁泰纺织股份有限公司，山东 淄博255100）

缝线是制衣生产的主要辅料之一，每件产品耗用缝线成本0.3元左右，同时是易损辅料，因此合理预算用量对生产顺利进行和成本的有效控制有极其重要的作用。年度预算时间跨度长，不确定性因素多，预算方法的确定对用量的预算准确性起了决定性的作用。通过查阅相关资料结合惯用方法，现有的方法主要有5种，本文就常用的5种方法的进行探讨，探索最适用的预算方法。

1 对5种方法的适用性分析比较

1.1 公式法

已有文献［1－2］研究根据各种线迹的曲线结构，计算出单位线迹长度的缝线耗用量，求得计算公式（见表1）。通过用公式计算各种线迹规格长度使用的耗用量，求和得出需耗用总米数。这种方法计算科学严谨，相对准确，但是需要提前预算款式、规格尺寸。

表1 1m线迹的缝线耗用量计算公式

1.2 倍数法

倍数法［1］即事先确定各种线迹缝线耗用量长度与线迹长度的比值，根据X＝L／F（式中：X－比值；L－缝线耗用量长度；F－线迹长度），从而求得不同线迹缝线耗用量长度；这种方法优缺点同公式法。

1.3 定长法

利用测线装置直接测量单件样衣的作业用线量，得到样品服装的用线量，根据生产计划，计算缝线计划需用量。这种方法对单件产品相对准确，但是需要确定损耗率和不同款式分别测量。

1.4 测重法

通过直接测量在样衣生产前后的缝线重量的差异，得到样衣消耗缝线重量，再根据试验确定缝线重量跟缝线长度的比值，从而换算得到样衣的缝线消耗长度。这种方法优缺点同定长法。

1.5 历史资料参照

1.5.1 以某几个订单数据为基准

根据不同订单的单耗进行平均，得到每件产品平均用线量。此方法考虑了不同订单模式的用线量，有一定准确性，但是因为时间跨度小，订单长短袖等单耗差距大，存在一定偏差。

1.5.2 以历史时期数据为基准

根据以往不同月份所生产产品总量所消耗的缝线总量，进行平均计算，得到全年平均用量，此方法因参照时间长，准确度较高，不足之处是未考虑产品结构（比如长短袖），同样存在一定偏差。

1.6 比较

以上5种方法各有优缺点，通过对以上5种方法探讨，可归纳出结果如表2所示。

表2 5种方法的对比

从表2中可以看出，5种方法对长期预测都存在局限性，不能满足年度预测的要求。

2 对预算方法进行探讨

2.1 产品结构数据

由表3可以看出，2012年此工厂生产的订单有欧洲市场、美洲市场、国内市场三个市场区分，有男式长袖、男式短袖、女士长袖三个款式区分。

表3 2012年生产订单

2.2 每件产品耗用面料米数比较

由表4每件产品耗用面料米数可以看出，根据市场和长短袖，每件产品耗用的面料各不相同，具有较大差异。

2.3 生产部门常用的理论用线量标准

生产部门常用理论用线量为仅区分长、短袖，长袖产品每件用线115m，短袖每件用线105m。

2.4 数据分析

数学分析中常用因子分析或聚类分析［3－4］进行数据分析，因子分析法就是将相关比较密切的变量归在同一类中，以较少的几个因子反映原资料的大部分信息。聚类分析是依据实验数据本身所具有的定性或定量的特征来对大量的数据进行分组归类以了解数据集的内在结构，并且对每一个数据集进行描述的过程。根据此思路，综合考虑现有数据，建立表5预测模型，从而根据变量进行预测。

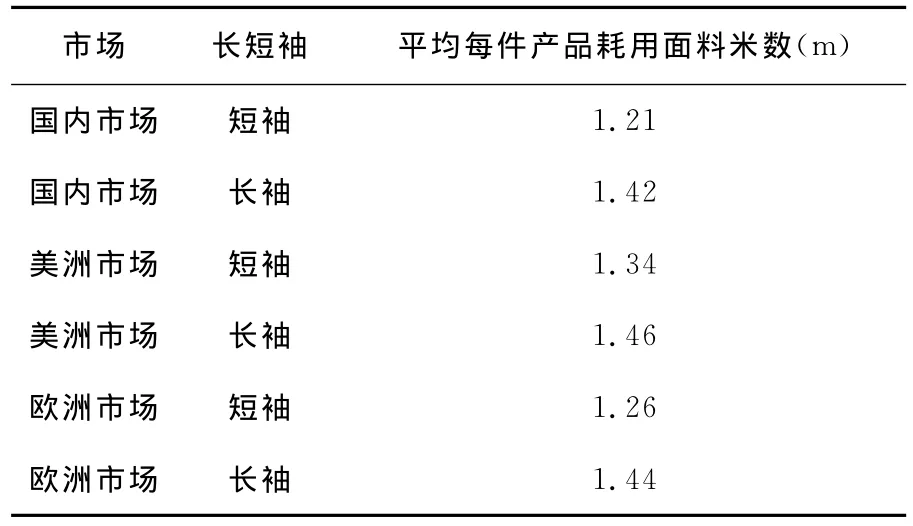
表4 每件产品耗用面料米数比较

2.5 数据验证

年度预算，跨度时间长，不确定性因素多，根据此预测模型综合考虑各方面，可参照在足够长时期内，一定环境、条件下消耗情况，同时又以经验数据作支持，如表6、表7中，经2013年1～10月份数据验证，实际与预算差异率为2.0%，准确度较高。

2.6 预测方法的综合评判

采用模糊综合评判方法来评价此预测方法［5－6］相关理论如下：

定义评判因素集X＝｛预测的精确度，预测费用，预测方法的复杂性，预测方法的适应范围，预测的时限长短｝。评语集合为y＝｛优，良，中，一般，差｝，根据模糊隶属关系原则，把各级相对于“最优”的程度分别用0.9，0.7，0.5，0.3，0.1表示，则y＝｛0.9，0.7，0.5，0.3，0.1｝.每一种预测方法都有各自的特点和适应范围，相关的研究成果见表8。

表5 缝线用量综合考虑法预测模型

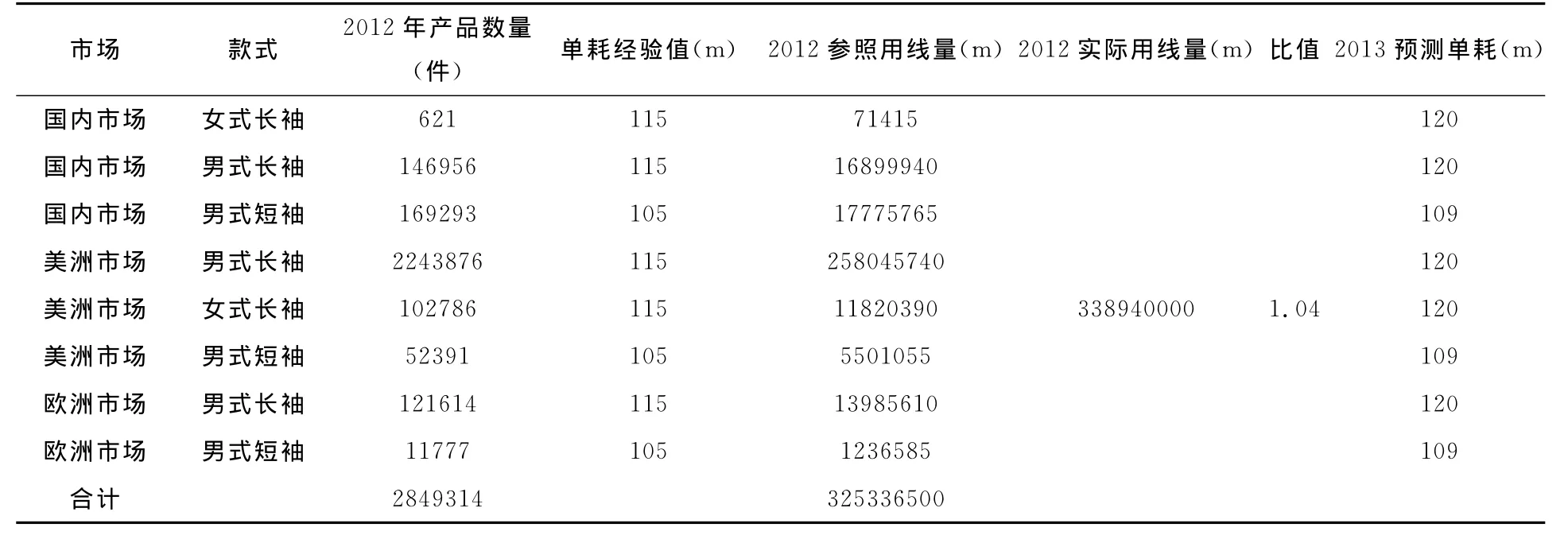
表6 2012年度实际用线及2013年度预测用量

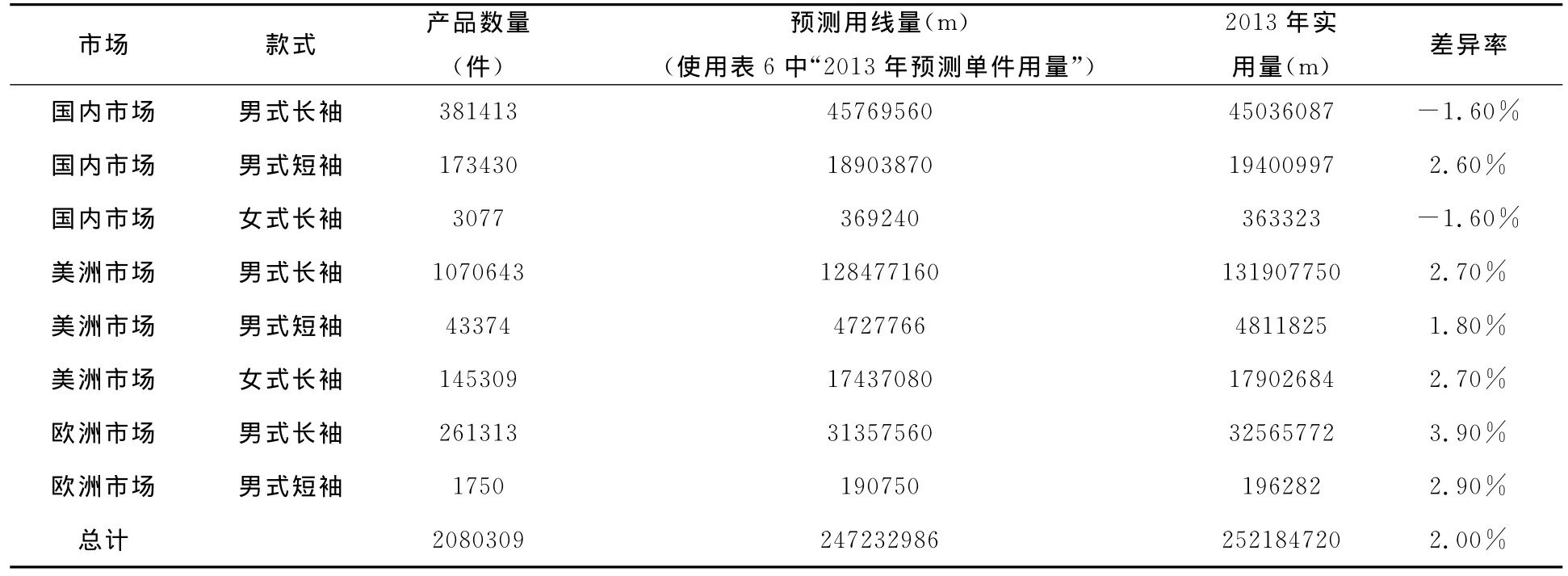
表7 2013年1～10月总用线量预算与实际差异比较

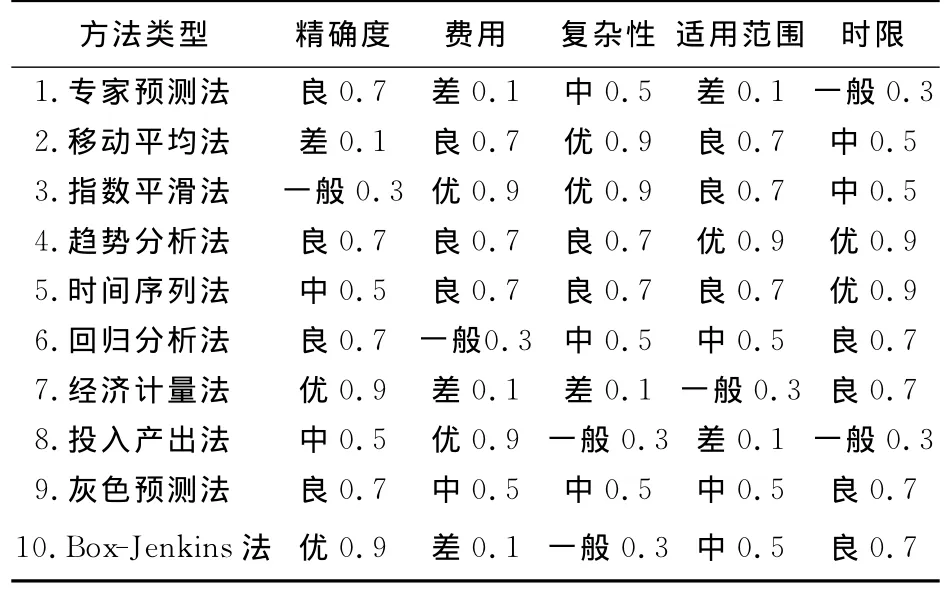
表8 预测方法比较

R1，R2，R3，R4，R5分别表示精确度、费用、复杂性、适用范围和时限.在确定了R和y的前提下，我们可通过给定X中各因素的相对权重A，再采用模糊变换 B＝A0R，若令 A＝（0.5，0.1，0.2，0.1，0.1），将R代入，求得综合评判结果.

对前述六种方法的分析后，可将前四种发放归结为“经济计量法”范畴，历史资料参照法归结为“移动平均法”，“综合考虑法”中R1值为0.9，R2值同“移动平均法”为0.9，R3值同“回归分析法”为0.5，R4值为0.9，R5值同“回归分析法”为0.7，从而建立六种方法的评价体系：

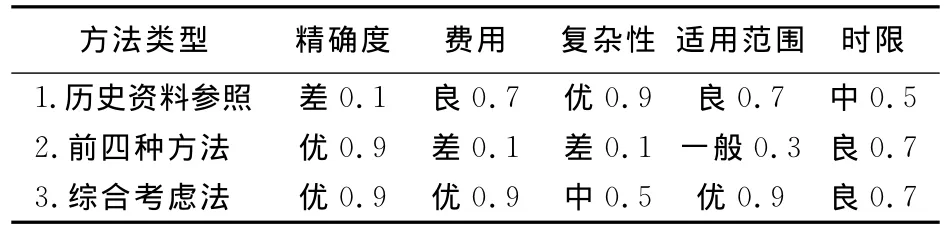
表9 预测方法比较

令 A＝（0.5，0.1，0.2，0.1，0.1），将 R 代入，求得综合评判结果 .B＝A0R＝ （0.42，0.58，0.8），则“综合考虑法”方法最优。

3 结论

综合分析以上6种预算方法，“综合考虑法”建立了预测模型，能够方便的使用已往的数据进行分析和后期跟踪，合理性较高，因此年度预算中可用“综合考虑法”进行缝线用量的预算。

［1］姚晓林.针织服装缝线用量的估算方法［J］.上海纺织科技，2002，30（2）：37－38.

［2］倪红.基于均匀设计试验方案的平缝作业下缝纫用量的估算［J］.苏州大学学报（工科版），2012，32（3）：61—12.

［3］游家兴.如何正确运用因子分析法进行综合评价［J］.统计教育，2003，（5）：10—10.

［4］李新蕊.主成分分析、因子分析、聚类分析的比较与应用［J］.山东教育学院学报，2007，（6）：23—24.

［5］程昳.常用预测方法及评价综述［J］.四川师范大学学报（自然科学版），2002，25（1）：72—73.

［6］曾珍香，谢素卿.常用预测方法的模糊综合评判模型［J］.预测，1993，（1）：60—64.